深井、超深井套管柱强度设计磨损分析*

杜 聪，张建兵，鞠录岩，罗 楚

（西安石油大学，陕西 西安 710065）

井筒完整性是当前石油工程的关注热点，套管柱的完整性对井筒完整性具有直接影响。随着深井、超深井建井数量的增加，苛刻环境下的套管柱设计面临的挑战也越来越多，国内外石油公司都在不断探索更加完善的套管柱强度设计方法，以提升套管柱成本的经济性与服役期间的安全性。当前国内外普遍采用的套管柱强度设计方法为安全系数法，安全系数法是基于对套管本身强度的认识和套管柱服役期间所承受载荷的正确认识。由于国内外关于环境因素对套管强度的影响和套管柱载荷的考虑与认识不同，各大石油公司的套管柱强度设计作法也有所不同。

钻井过程中的套管磨损在所难免，深井、超深井钻进时间越长，套管磨损越严重，套管磨损导致的强度降低尤其不能忽略。套管磨损轻则降低套管柱的抗挤强度和抗内压强度，给后续的钻井、完井、采油和修井作业带来安全隐患，重则造成套管柱挤毁、变形或泄漏，甚至造成全井报废［1］。磨损前套管的强度值可以通过查阅有关标准手册或者通过API 方法等传统经验公式计算，但是对于磨损后的套管目前还没有特别准确且通用的计算公式［2］。如何估算这种“月牙形磨损”的套管强度一直是石油行业的研究方向，这直接关系到套管柱设计的安全性。

1 磨损槽深度计算套管强度

英国石油公司《套管柱设计手册》和壳牌公司《油管和套管设计指南》都是通过计算磨损槽深度来考虑磨损后的套管强度。随着磨损槽加深，钻杆接头与套管的接触面积将会增大，在恒定侧向力情况下这相当于接触压力降低。当接触压力达到1.7 MPa，套管迅速由磨粒磨损变为粘着磨损且磨损率开始增大，这意味着钻杆接头和套管初次接触时产生的高初始接触压力会导致套管磨损，随后磨损迅速下降为稳定的磨粒磨损状态。可通过以下步骤对套管磨损进行预测。

（1） 确定需要参数。

钻头类型及表面材料，泥浆类型（水基或油基），所测深度套管侧向力，钻杆伸缩量，狗腿严重度，钻杆的总旋转小时和钻速等。

（2） 根据狗腿度、侧向力、钻杆伸缩量等确定套管的磨损因数f。

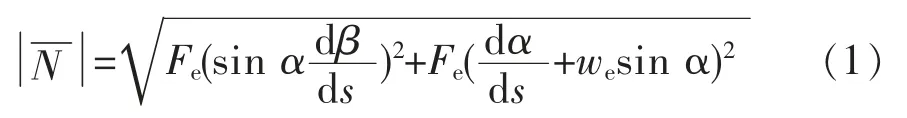
式中 Fe—— 有效作用力，N；

s —— 套管长度，m；

β —— 方位角，（°）；

α —— 井斜角，（°）；

we—— 单位长度有效质量，kg/m。

（3） 根据等效旋转小时、磨损因数和钻具接头直径确定套管磨损量。

等效旋转小时hr为：

式中 n ——转速，r/min；

h —— 旋转时间，h。

单位长度的磨损量V 为：

w —— 套管磨损深度，mm；

Dt—— 钻杆接头直径，mm；

L —— 钻层深度，m；

R —— 钻进速度，m/h。

（4） 将磨损量转化为新月形磨损深度，确定套管磨损率wr。

式中 t —— 套管壁厚，mm。

将预测磨损量与允许磨损量进行比较，确保磨损量在安全系数内。不过在磨损率敏感性分析中磨损变化很大，分支井、大范围扩孔、套管磨损不能用上述公式计算、高温高压井，应进行更详细的套管磨损分析。

根据套管磨损量可以计算出磨损下降系数fw：

API 套管抗内压强度在巴洛公式计算的基础上乘以fw。如果有详细的厚度数据，可以使用实际测量数据计算套管磨损的修正API 内部屈服强度。在抗内压强度计算时应满足：

式中 p —— 套管压力差，MPa；

Db—— 抗内压安全系数，Db≥1.1；

fT—— 温度影响因素；

pi—— 屈服时的内部压力，MPa。

API 套管的抗挤强度与剩余壁厚成正比。根据剩余壁厚，采用直接比例法计算出挤毁压力。例如套管磨损了20%，那么抗挤强度是新套管的80%。壳牌公司《油管和套管设计指南》同时对腐蚀套管的强度进行分析，在进行抗内压计算时壁厚应减去最大点蚀深度；抗挤强度取决于套管的径壁比D/t（D为套管直径），壁厚应减去平均点蚀深度；在进行抗拉强度计算时，抗拉强度的减少量与材料腐蚀率成正比。

2 偏心筒模型计算套管强度

根据套管磨损深度进行抗内压强度和抗挤强度设计，相当于使用均匀磨损模型进行计算，这种线性计算过于保守。在此基础上相关学者还采用偏心筒模型通过计算环向应力、屈服强度等对磨损套管进行研究。

2.1 磨损对抗内压强度影响

根据套管环向应力在套管内壁处较高、在套管外壁处较低的特点，可通过环向应力和套管变形来计算磨损套管的抗内压强度［3-7］。使用图1 所示开槽环模型计算磨损套管的环向应力，大小相当于环向力的损失量加上磨损部位的内部压力：

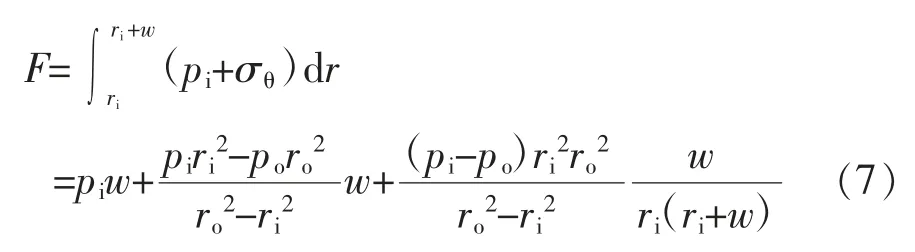
式中 po—— 套管外压，MPa；

σθ—— 环向应力，MPa；

ri—— 套管内径，mm；

ro—— 套管外径，mm。

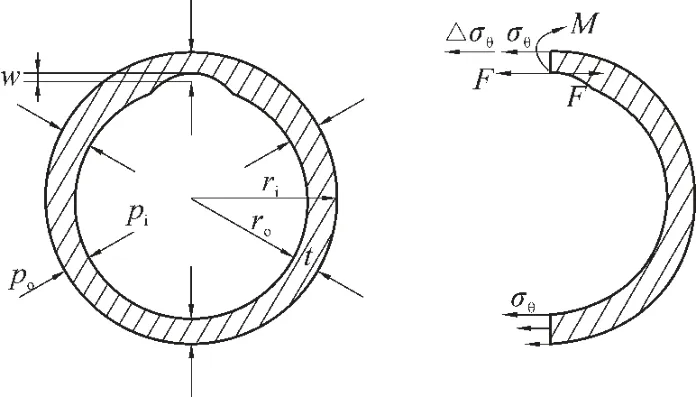
图1 磨损套管受力示意

相比未磨损套管，磨损处的环向应力的增量为：

为了保持力矩平衡，磨损套管还会产生一个感应弯矩。不考虑套管变形的影响，该弯矩M 为：

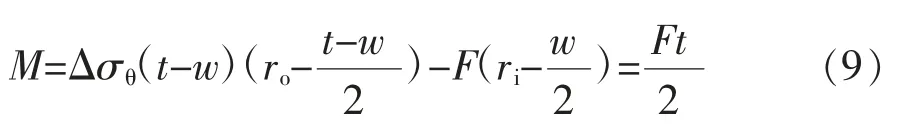
这个弯矩会在套管上产生弯曲应力：

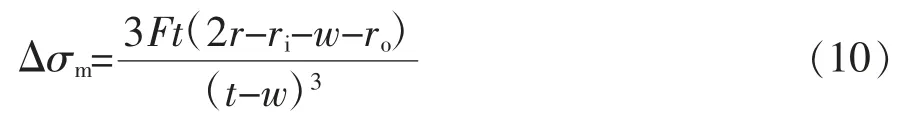
其中，ri+w≤r≤ro。

将环向应力增量和考虑套管变形的弯曲应力（套管变形的弯曲应力等于Δσm与0.65-0.65w/t 的乘积）相叠加，可得到磨损套管的环向应力：

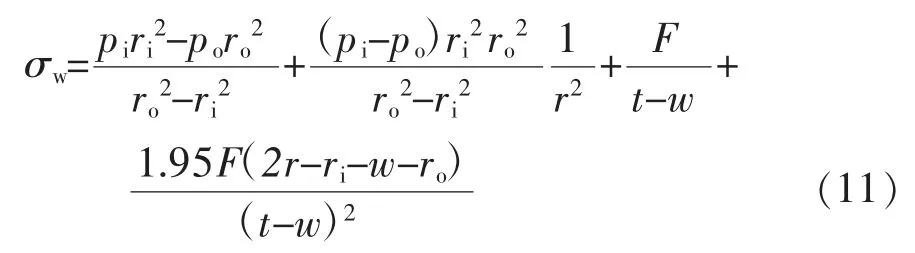
通过套管三轴应力条件下的Von Mises 屈服准则确定磨损套管的屈服强度Yp：

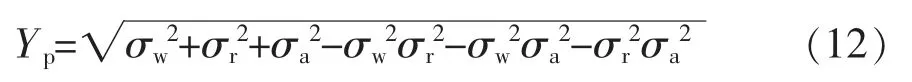
式中 Yp—— 磨损套管的屈服强度，MPa；

σa—— 套管轴向应力，MPa；

σr—— 套管径向应力，MPa。

套管的抗内压强度P 为：

在不考虑局部弯曲的情况下，采用此方法计算的环向应力与均匀磨损模型得到的环向应力基本相同；但考虑局部弯曲时，由此方法计算的环向应力比均匀磨损模型得到的高。

2.2 磨损对抗挤强度影响

抗挤强度通常根据Von Mises 和Tresca 屈服准则建立，没有充分考虑中间主应力效应和拉压强度差效应（即SD 效应）对套管挤毁压力的影响［8］。Bjorn Brechan［9］等进行了不同磨损状态下 Φ139.7 mm×7.72 mm N80 套管的挤毁试验，发现：套管挤毁时，未磨损套管处于塑性挤毁阶段；均匀磨损套管由塑性挤毁阶段进入弹性挤毁阶段；局部磨损套管仍处于塑性挤毁阶段，挤毁压力的降幅很小。可以看出，采用均匀磨损模型计算出的结果和实际情况相比误差较大。Φ139.7 mm×7.72 mm N80 套管磨损部位受力分析见表1。

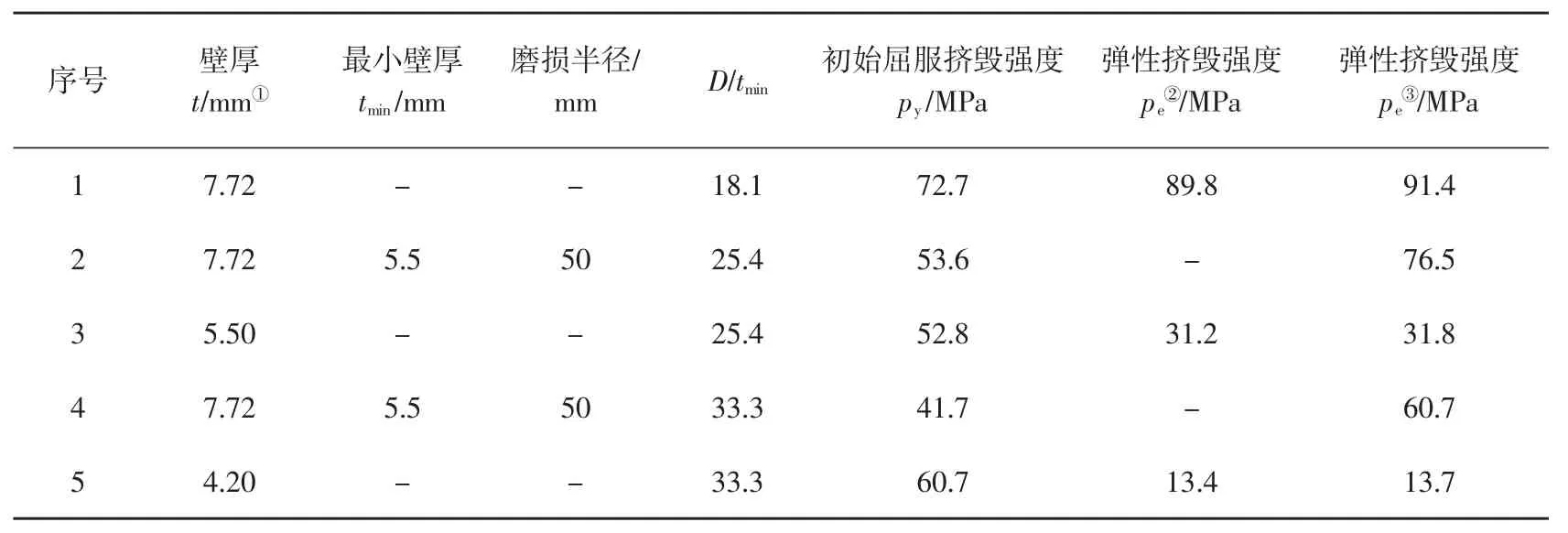
表1 Φ139.7 mm×7.72 mm N80 套管磨损部位受力分析

因此，文献［10］认为磨损套管的抗挤强度与屈服强度有关。偏心筒套管模型的挤毁强度为：

式中 pw—— 磨损套管挤毁强度，MPa。

通过偏心筒模型，考虑磨损套管的挤毁强度、椭圆度和残余应力等，估算出磨损套管的预计挤毁强度：

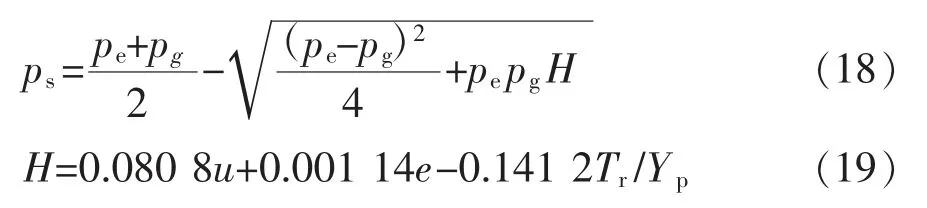
式中 H —— 套管偏差；

u —— 椭圆度，%；

e —— 偏心率，%；

Tr—— 环向残余应力，MPa；

pg—— 轴向力作用下屈服挤毁强度，MPa。

磨损套管的挤毁压力：

3 有限元分析与对比

为验证上述两种理论的准确性，将Φ244.5 mm×11.99 mm 的P110 磨损套管的计算结果和有限元分析（FEA）进行对比。有限元分析时假设：套管为各向同性的弹性体，忽略套管缺陷和其他载荷，为避免固定约束的影响，套管长度取外径的10 倍以上，为3 000 mm。套管弹性模量取210 GPa，泊松比0.3，密度7 850 kg/m3，屈服强度758 MPa。在Workbench 仿真平台中对结构进行网格划分，划分为6 068 个单元和33 670 个节点，网格划分如图2 所示。

磨损套管的抗内压强度与磨损率关系如图3 所示，抗内压强度随着套管磨损而线性减小［11］，当磨损50%抗内压强度降低了50%。采用偏心筒模型计算结果更加准确，与有限元分析误差在5%以内。

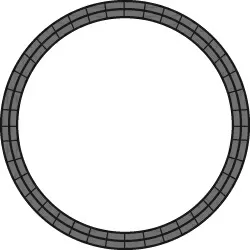
图2 套管网格划分

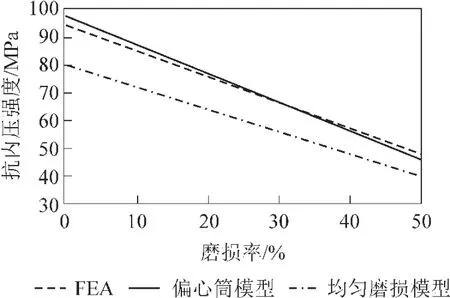
图3 套管剩余抗内压强度与磨损率关系

磨损后套管的抗挤强度与磨损率关系如图4 所示。根据磨损槽深度计算的抗挤强度线性下降；而FEA 和偏心筒模型计算结果基本吻合，只在20%磨损前线性下降；当套管磨损超过50%，抗挤强度很小，几乎失去抵抗外部挤压作用。虽然常采用的线性下降规律并不准确，但可以通过安全系数弥补误差，使得线性计算可以满足实际需求［9］。

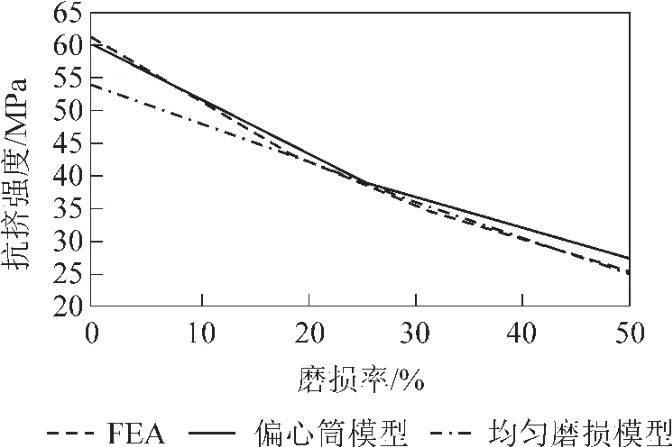
图4 套管剩余抗挤强度与磨损率关系

4 深井、超深井套管强度计算

在深井、超深井中由于温度和压力变化较大，环空压力显著增加，导致套管柱或生产尾管失效风险进一步加大。传统拉梅方程并没有考虑温度的影响，计算结果不能满足实际需要。Shen Z［12］先通过无磨损套管模型考虑热应力，再采用叠加原理对磨损套管进行分析，以确定月牙形磨损部分的应力分布。无磨损套管模型在考虑热应力时的环向应力为：

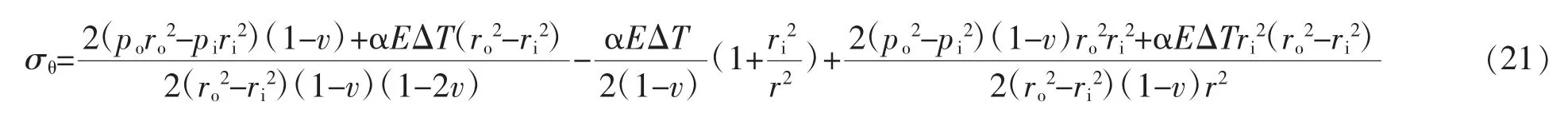
式中 ΔT —— 流体与地层温差，℃；

E —— 杨氏模量，Pa；

v —— 泊松比。

磨损套管如图5 所示，磨损部位壁厚从t 减小到tw并产生额外应力：

式中 r2—— 钻具接头半径，mm；

tw—— 磨损后壁厚，mm；

rn—— 磨损后内径，mm。

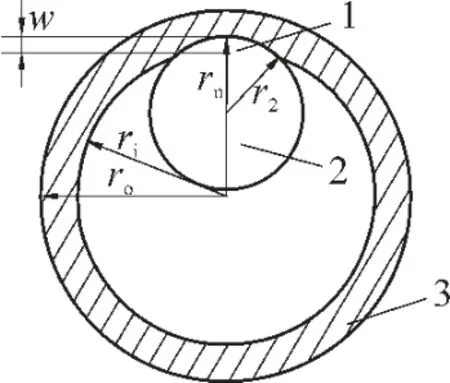
图5 磨损套管示意

将上述应力叠加得到套管的环向应力：

套管磨损部位受到预期的应力集中，随着磨损的增加和温度的升高，环向应力会急剧增加。将环向应力带入公式（12）可得到套管的屈服强度，从而得到套管磨损后的抗挤强度和抗内压强度［13-14］。

5 认识与结论

磨损套管主要从均匀磨损模型和偏心筒模型两个方面进行强度研究。分析发现，通过API 均匀磨损模型得到的套管强度存在低估，而采用偏心筒模型计算出的结果符合套管实际力学特性。

套管的抗内压强度和抗挤强度都随着磨损率增大而减小，不同的是抗内压强度随着磨损线性减小，抗挤强度只在低磨损时线性减小。

深井、超深井由于钻井时间长、井底温度高，相比普通井环向应力显著增加，在计算时可采用叠加原理同时考虑温度和磨损的影响。