基于广义混合元加筋板的振动特性分析1)
陈秀涛 卿光辉
(中国民航大学航空工程学院,天津300300)
通常情况下,带有加强筋的板壳结构具有刚度大、耗材少和重量轻等特点,因此被广泛应用于各类实际工程中。但由于加筋结构的振动行为对整体结构的稳定性影响十分显著,所以有关加筋结构的振动特性分析一直是国内外学者研究的热点问题。
Mukherjee 等[1]和 Mukhopadhyay 等[2]对加筋结构振动分析的早期文献进行了综述:由于加筋结构的复杂性,基于位移有限元模型的数值分析方法最为普遍。Trkmen 等[3]提出了暴露于冲击波的加筋板的位移有限元分析模型,并进行了实验研究。Zhao等[4]使用能量方法,研究了简单支撑的交叉加筋多层圆柱壳的自由振动。Rikards 等[5]发展了一种精度较高的三角形单元,研究了加筋复合材料层合壳的自由振动。Guo 等[6]对加筋层合板结构提出了分层有限元模型,并对这类结构进行了屈曲分析。游翔宇等[7]基于光滑有限元法对加筋板的自由振动进行了研究。
值得说明的是,一般位移有限元法是采用有限的节点代替了真实结构中无穷多的点,结果导致有限元模型比真实模型的刚度大,故而固有频率结果大于真实解。从理论上讲,由于合理地引入非协调位移项,使其近似多项式的阶次完备,致使非协调元的柔性增加。系统控制方程的柔性也相应地增加,因而采用非协调元的模型可以得到精度更高的数值结果。然而,即使采用收敛性较好的非协调位移元分析加筋板的振动特性问题,其相应的有限元模型的刚度也是偏硬的,因而在有限元网格较稀疏的情况下,固有频率结果通常是大于真实解的。
近些年来,一些研究人员应用Hamilton 正则方程半解析法分析加筋层合结构[8]或厚度不连续结构的振动特性问题[9]。Hamilton 正则方程半解析法分析板壳结构的显著优势是允许材料和几何特性沿厚度方向改变,并可以方便地分析层合板壳结构类的振动问题。通常情况下,基于Hamilton 正则方程半解析法的模型,数值结果相对比较准确。但是,该方法有一个明显的缺点,即由于层合板壳类结构的每层在面域内对位移变量和面外应力变量进行了有限元离散,因而每一层的单元组装后导致规模较大的数值矩阵。在形成结构整体的控制方程前需要对每一层的数值矩阵分别进行关于厚度变量的指数矩阵运算,这一过程的数值运算成本高。另一方面,完成了每一层矩阵指数运算后,为保证不同材料层的层间位移变量和应力变量的连续性,又要对各层的控制方程进行乘积运算,这一计算步骤也需要一定的时间。总之,Hamilton 正则方程半解析法面对工程中庞大的结构问题,单元离散的数量大,数值运算相对于常规的有限元位移法来说,矩阵指数运算量大,时间消耗大。
传统的混合有限元法有很多优点,例如,通常只需C0连续的插值多项式来近似表达待求的场量,位移和应力计算结果精度高。最近,Qing 等[10]结合最小势能原理和H–R 变分原理建立了分析静力学问题的非协调广义混合元。文献[11] 扩展了这种非协调广义混合元的应用范畴。
本文在文献 [10-11] 的基础上,根据 Hamilton原理,首先建立考虑结构振动特性的广义混合变分原理,然后建立了非协调广义混合元的动力学模型,用于加筋板的振动特性分析。
1 位移元的振动特征方程
通常情况下,以位移元为基础的无阻尼自由振动方程[12]为
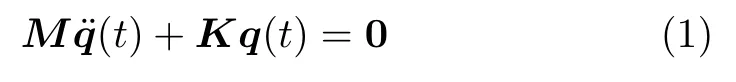
式中,M表示结构的质量矩阵,为单元的一致质量矩阵,N表示形函数矩阵,ρ表示材料的密度,V表示连续体的体积,K表示结构的刚度矩阵,是单元的刚度矩阵,B为应变矩阵,D是材料的弹性矩阵。
设q(t) 为待求的解,考虑简谐运动问题时,位移解的表达形式为

式中,Φ表示固有振型,ω表示对应固有振型的频率。
将式 (2) 代入式 (1) 可得到无阻尼自由振动的特征方程为
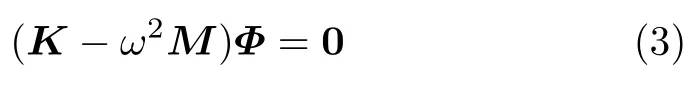
对式(3) 的求解方法较多,例如,逆迭代法、子空间迭代法和行列式搜索法等。
2 广义混合元的振动特征方程
根据广义混合变分原理[13],可设结构的混合能(包括应变能和余能) 为
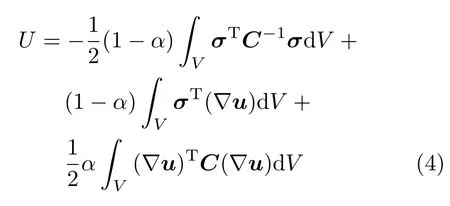
式中,σ表示应力向量,C表示材料的刚度系数矩阵,∇表示微分算子,u表示位移向量。
处于自由振动状态下的结构的动能为
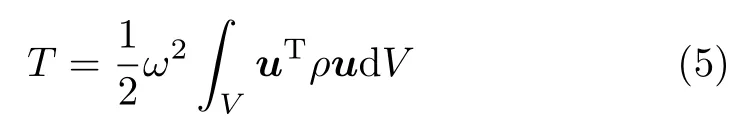
式中,ω表示固有频率,ρ表示材料密度。
考虑动力学问题的Hamilton 变分原理为

因此含有固有频率ω参数的广义混合变分原理可表示为
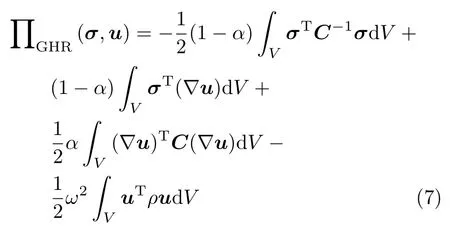
式中,参数α的取值范围为 0α1。
参考文献[10-11] 的推导过程,由式(7) 可得到六面体非协调广义混合单元的自由振动特征方程为

式中,h为单元柔度矩阵,g为单元杠杆矩阵,pe表示单元节点的应力参数,Φe表示单元固有振型参数,
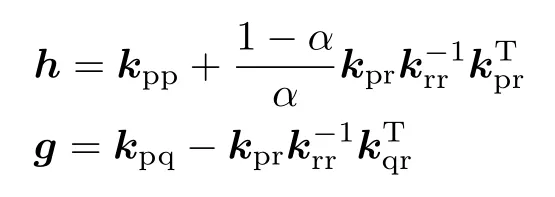

各式中的形函数矩阵N和非协调项形函数矩阵Nr表达形式可参见文献[10-11]。
由式(8) 可导出
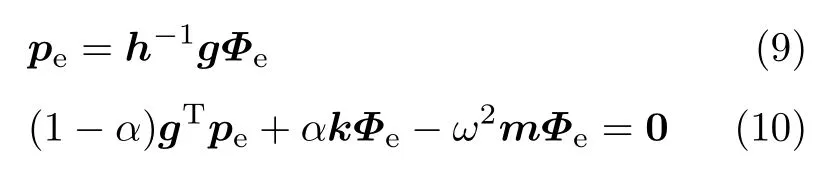
将式 (9) 代入式 (10) 中有

其中,刚度矩阵κ=αk+(1−α)gTh−1g。
式(11)表明六面体非协调广义混合元的刚度矩阵κ与柔度矩阵g相关,参数α的取值范围为0∼1, 并且不同的取值可得到不同的刚度矩阵。若式 (7) 中α= 1,则式 (11) 中的κ与位移元下的刚度矩阵一致,同为基于最小势能原理的非协调位移元的刚度矩阵。α1 时,其不同的取值可以调节刚度矩阵柔性。文献[14] 推导含参数α的广义混合元模型时,小变形线性弹性问题是最基本的假设。另一方面,假设含参数α的广义混合元模型的应变能与精确的应变能相等。基于这一假设,文献 [14] 导出了参数α= 0.75 的最优值。因此,就小变形线性弹性问题而言,广义混合元模型中的α= 0.75 对计算结果的最主要影响是数值解更接近问题的真实解。
对式(11)求和可得整体有限元模型的振动特性方程为
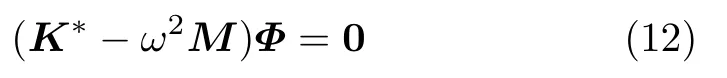
关于非协调广义混合元模型施加边界条件的方法:最终的振动特性方程 (12) 中只含有位移变量。因此方程(12) 只需考虑位移边界条件的引入,其引入方法与位移元法中的方法相同。
3 实例分析
以下数值分析均采用式(12)对算例进行数值分析,其中参数α=0.75。此外,在关于加筋板的算例中,为了提高计算效率,对式(12) 中的单元质量矩阵采用集中质量矩阵的形式。
3.1 层合板的自由振动特性分析
如图 1 所示的三层板,每层均为正交异性材料,坐标轴沿弹性主方向,上、下两层材料相同。令分别表示第一和第二层的C11值,ρ1和ρ2分别是第一层和第二层材料的密度。当δ= 1,γ= 1 时,该板即为一单层正交异性板,板长度a和宽度b,a=b,厚度h,h/a=0.1,h1/h=h3/h=0.1,h2/h=0.8。边界条件如图2 所示,为四边简支,即当x=0 和x=a时,u=w=0,当y=0 和y=b时,v=w=0。刚度系数比为


图1 层合板尺寸图

图2 四边简支约束
以下通过改变网格密度来讨论非协调广义混合元的收敛性。
在γ= 1 和δ= 1 的模型下,在x方向和y方向划分同等单元(从2 个单元递增到12 个单元),在厚度方向z划分10 个单元,保持不变。
第一阶固有频率的收敛曲线如图3 所示。从图中可以明显看出,随着网格密度的增加,通过非协调位移元和非协调广义混合元计算的频率结果都逐渐趋于平稳。当网格密度为8×8×10 时,两种方法的结果都逼近精确解,但非协调广义混合元的结果更加精确。
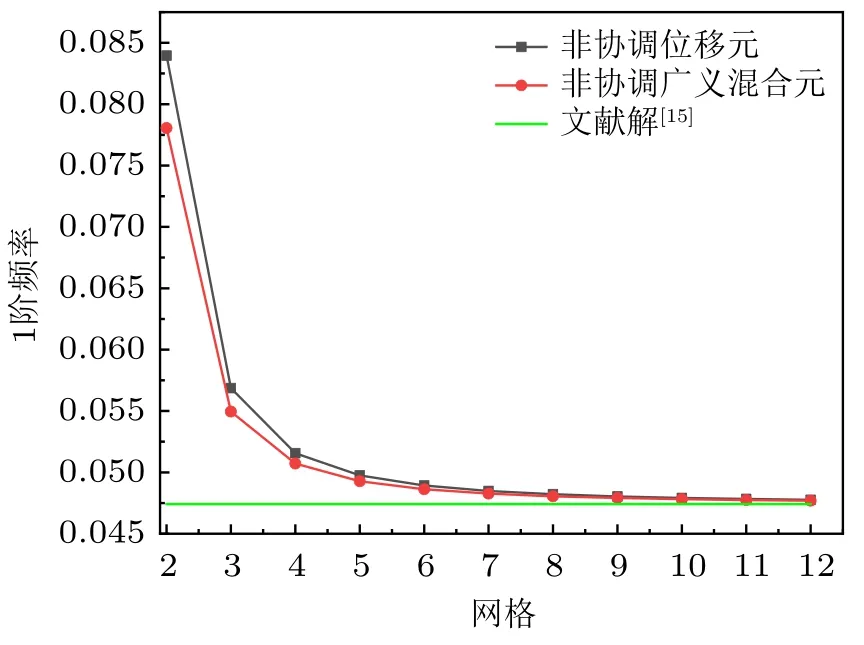
图3 不同网格密度下的1 阶固有频率
以下根据δ,γ的不同取值,分别求其一阶固有频率。网格划分情况如图 4 所示。两种有限元模型的固有频率结果见表 1,且两种模型的 1 阶振型图一致,如图5 所示。
比较表1 中的数据,不难看出,非协调位移元的结果高于文献解。这是因为位移元模型的刚度相对于实际的模型偏硬。在网格模型相同的情况下,因为非协调广义混合元模型的刚度更接近真实结构,所以本文的非协调广义混合元的结果优于非协调位移元。这一结论与文献[14] 中的相关论述相同。

图4 层合板网格图
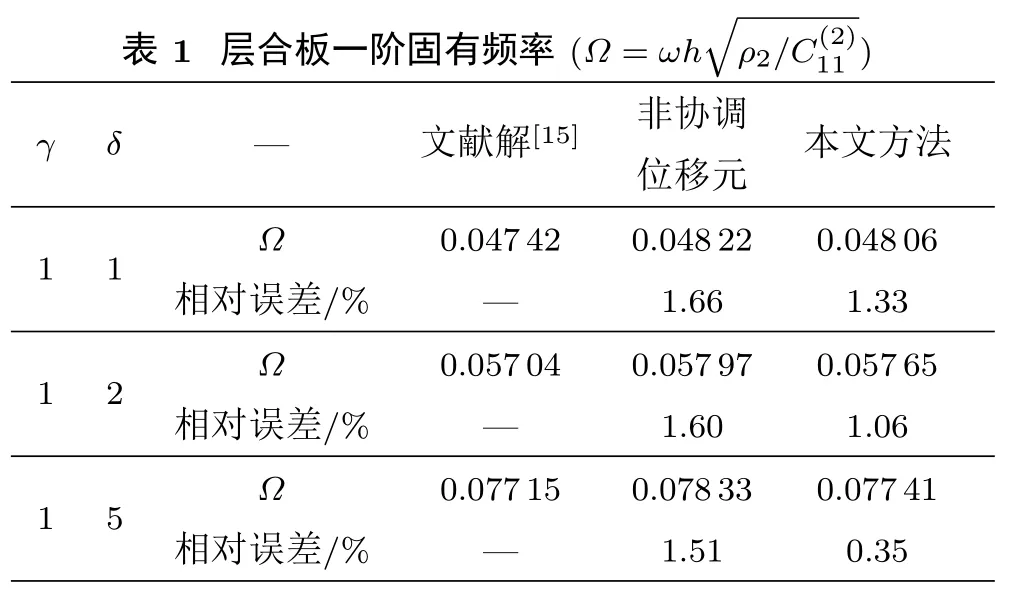
√/C(2)11 )本文方法0.048 06 1.33 0.057 65 1.06 150.077 41相对误差/% — 1.51 0.35
图5 1 阶振型图
3.2 单加强筋偏心加筋板的自由振动特性分析
带有单加强筋的偏心加筋板,尺寸图如图6 所示,材料参数为:弹性模量E= 68.7 GPa,泊松比ν= 0.29,密度ρ= 2823 kg/m3。几何参数:a=b= 0.203 2 m,t= 0.001 371 6 m,w=0.006 35 m,h=0.012 7 m,边界条件为四边固支,如图 7 所示,当x=0 和x=a时,u=v=w=0,当y=0 和y=a时,u=v=w=0。对该结构的振动特性进行分析。
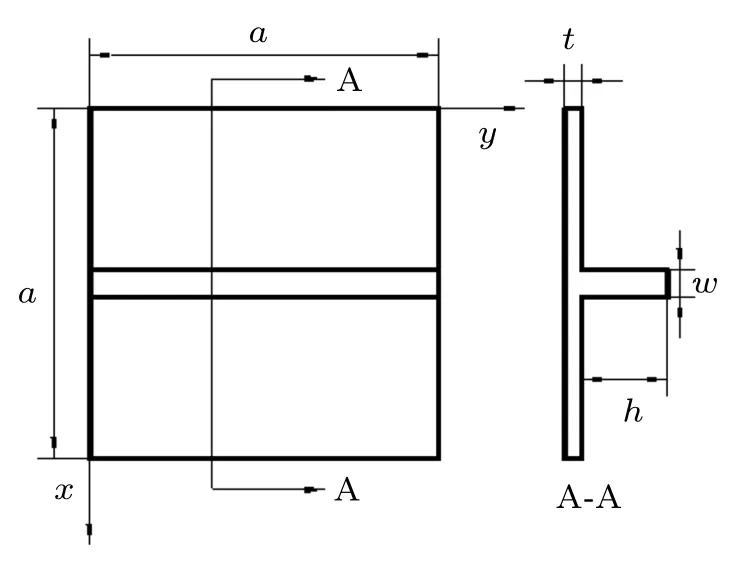
图6 单加强筋偏心加筋板尺寸图
将板部分划分成 27×27×1 个六面体单元,加强筋部分划分成1×27×8 个六面体单元,网格划分情况如图8 所示。两种有限元法的前4 阶固有频率结果见表2。前4 阶固有振型见图9,其中非协调位移元的结果由有限元商业软件Abaqus 得到。
图7 四边固支约束
图8 单加强筋偏心加筋板网格划分图
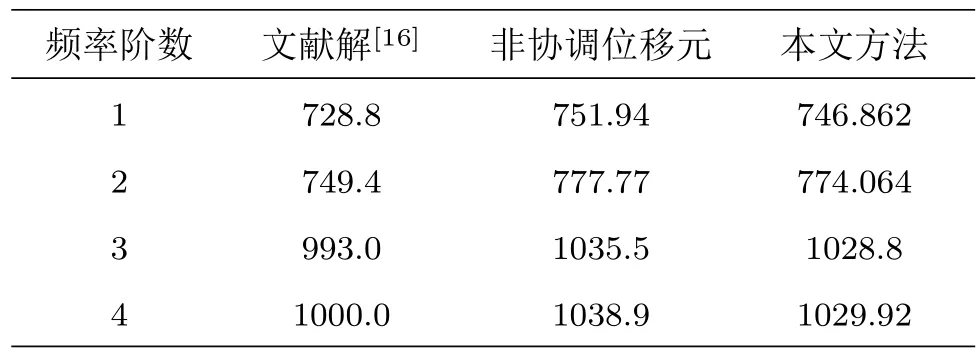
表2 单加强筋偏心加筋板前 4 阶固有频率(单位:Hz)
由表2 中数据可以看出,非协调广义混合元模型的固有频率值低于非协调位移元模型的结果数值,距离文献解更加接近,结果精度更高。
比较图9 中两种方法的前4 阶固有振型不难看出,非协调广义混合元模型和非协调位移元模型的固有振型几乎是一致的,这进一步验证了本文方法的正确性。
3.3 双加强筋偏心加筋板的自由振动特性分析
双加强筋偏心加筋层合板[8],尺寸如图10 所示,尺寸参数:a= 1.2 m,l= 0.4 m,t= 0.01 m,t1=0.02 m,w= 0.04 m,h= 0.08 m。板部分总共三层,每层均为正交异性材料,上下两个面层材料相同,假设面层的密度ρ1=1600 kg/m3,芯层的密度ρ1/ρ2=2,加强筋的材料参数与面层的一致。边界条件为四边固支,如图11 所示,当x=0 和x=a时,u=v=w= 0,当y=0和y=a时,u=v=w= 0。对该结构进行振动分析。

图9 单加强筋偏心加筋板的前4 阶固有振型
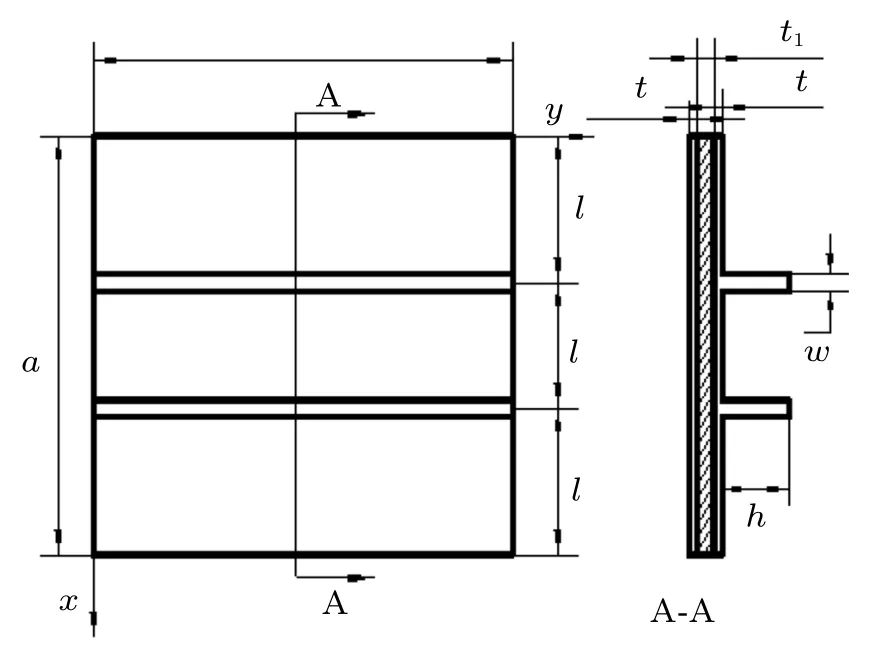
图10 双加强筋偏心加筋层合板
图11 四边固支约束
刚度系数比分别为

将平板网格划分成11×11×4,加强筋网格划分成1×14×4,网格划分情况如图12 所示。

图12 双加强筋偏心加筋板网格划分图
由表 3 可知,对于材料属性组成比较复杂的双加强筋偏心加筋层合板,非协调广义混合元的固有频率值明显低于非协调位移元模型的结果值,并且相应的前4 阶固有振型如图13 所示。
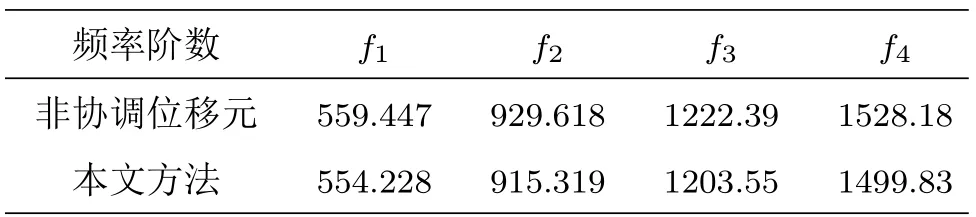
表3 双加强筋偏心加筋层合板前4 阶固有频率(单位:Hz)
4 结论
本文在非协调广义混合元理论的基础上,建立了关于应力和位移两类变量的自由振动特征方程。
非协调广义混合元的自由振动特征方程的明显特点是在消去应力变量时,柔度矩阵可对刚度矩阵中的系数进行调节,起到增加结构柔性的作用。
实例分析表明,基于非协调广义混合元模型的结果的精度高于非协调位移有限元的精度。从理论上讲,造成差别的主要原因是非协调位移有限元模型的刚度偏硬,会导致固有频率结果偏高,而非协调广义混合元模型的刚度更加接近真实情况,故而固有频率结果更接近真实解。
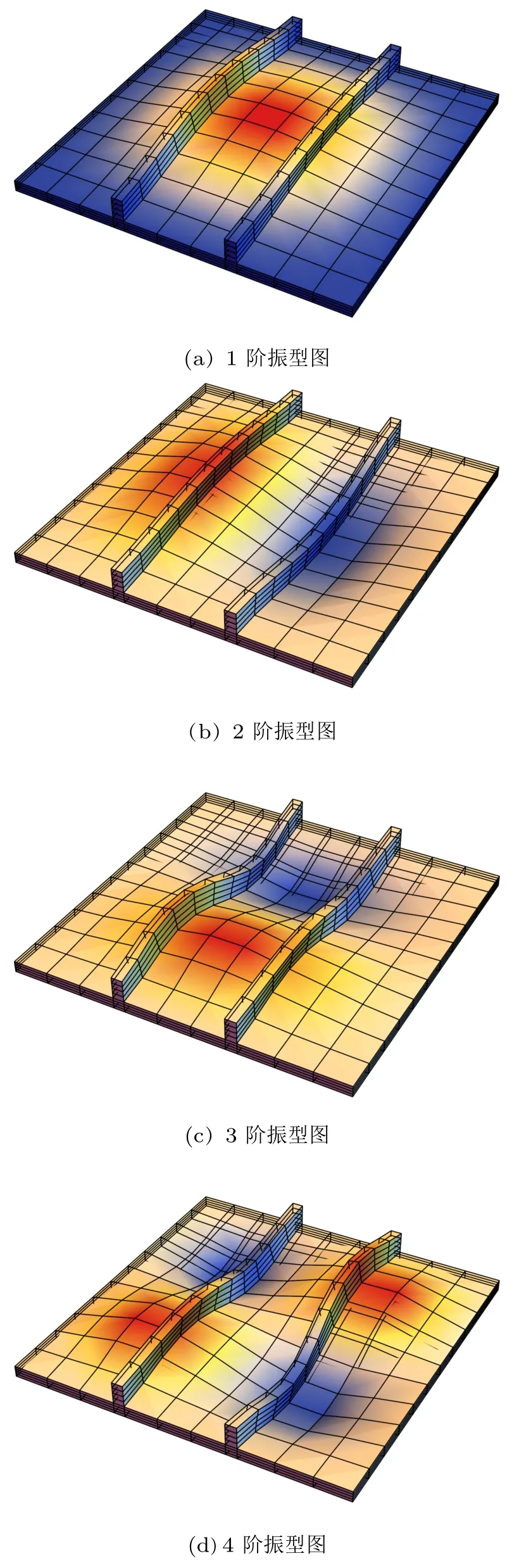
图13 双加强筋偏心加筋层合板前4 阶固有振型

