CRTSⅢ型板式无砟轨道减振过渡段动力特性分析

张世杰

（1.中铁第四勘察设计院集团有限公司，湖北 武汉430063； 2.铁路轨道安全服役湖北省重点实验室，湖北 武汉430063）

根据推进高铁站周边区域合理开发建设要求[1]，新建铁路车站选址应尽可能在中心城区或靠近城市建成区， 确保人民群众乘坐高铁出行便利。为了降低高速列车运行引起的振动对沿线居民的影响，对高速铁路采取有效的振动控制措施尤为必要。

我国目前已在武广、郑西、广深港等高速铁路项目中采取轨道减振措施， 铺设了减振型无砟轨道。 高速铁路减振型无砟轨道通过在轨道板下铺设隔振垫达到减振的目的， 减振地段较非减振地段轨道的整体刚度被大大削弱。 轨道结构整体刚度的突变会对车辆-轨道系统的振动产生影响[2-4]。刚度突变处车辆-轨道的动力作用一直受到我国学者的高度关注， 雷晓燕等利用解析求解法和叠加原理，以有砟轨道为研究对象，就轨道刚度突变对轨道结构振动的影响进行了研究[5-7]；蔡成标，翟婉明对客运专线道岔前后刚度过渡段的动力学性能开展研究， 提出了轨道刚度过渡段动力性能的评价指标以及过渡段合理长度的确定方法[8]；韦有信等利用有限单元法， 对高速铁路过渡段的动力学性能开展计算分析， 提出抛物线与三次多项式的组合曲线过渡方式为刚度最佳过渡方式[9]；王平，耿传志等针对地铁减振轨道两端刚度的合理过渡方式开展了研究[10-12]。

相对而言，既有研究成果对高速铁路无砟轨道减振过渡动力特性的讨论较少。 应用车辆-轨道耦合动力仿真分析模型， 对CRTSⅢ型板式无砟轨道减振过渡段的动力特性进行研究，以期为高速铁无砟轨道减振过渡段设计和养护提供参考。

1 轨道刚度过渡段动力分析模型

基于车辆-轨道耦合动力学理论[13-15]，建立包含非减振地段、 过渡段和减振地段的车辆-轨道耦合动力仿真模型，如图1 所示。 车辆模型简化为1 个车体、2 个转向架、4 个轮对， 共考虑35 个自由度。车体通过二系阻尼弹簧与转向架连接，转向架再通过一系阻尼弹簧与轮对连接。 钢轨采用离散单元点支承Timoshenko 梁模拟，截面选用60 kg/m 钢轨廓形，为减小纵向边界的影响，钢轨总长度取300 m；扣件和隔振垫板均采用6 自由度阻尼弹簧模拟；轨道板和底座板采用实体单元模拟，最大单元尺寸小于0.3 m；通过赋予隔振垫板弹簧不同的刚度，可以将轨道分为非减振地段、过渡段、减振地段；底座板下部通过弹簧单元与地基相连，弹簧刚度取4.3×108kN/m，与地基模量等效。车辆子系统和轨道子系统采用非线性赫兹接触进行耦合。

图1 车辆-轨道耦合动力分析模型示意图Fig.1 Diagram of vehicle track coupling dynamics model

2 计算参数

2.1 车辆、轨道参数

车辆子系统采用高速铁路CRH380 动车组参数，满载轴重为17 t，车辆定距17.5 m，轴距2.5 m，开行速度350 km/h。 轨道子系统考虑高速铁路CRTSIII 型板式无砟轨道减振， 该减振无砟轨道由钢轨、扣件、轨道板、自密实混凝土、减振垫、底座等组成。车辆、轨道主要参数见表1。除特别注明外，一般假定轨道平顺状态完好，无随机不平顺。

表1 车辆、轨道参数Tab.1 Vehicle and track parameters

2.2 计算工况

文献[4]提出有砟轨道过渡段整治可采用3～4层分层强化基础刚度的过渡方式。 文献[8]针对有砟轨道道岔两端刚度过渡参数进行分析， 提出了采用3～6 级过渡，每一级过渡长度取值9 m 的建议。 文献[11]提出地铁钢弹簧浮置板轨道两侧刚度过渡段的长度宜为10～15 m。结合前述研究成果，综合考虑高速铁路速度快、安全性、舒适性要求高的特点，将过渡级数的分析范围定为1～4 级，每一级过渡长度分析范围定为5～25 m（以轨道板的块数表示），详细工况见表2～表3，其中k0减振地段减振垫的刚度为0.02 N/mm3。

表2 分级过渡措施每一级过渡长度计算工况Tab.2 Calculation conditions of transition length of each stage of graded transition measures

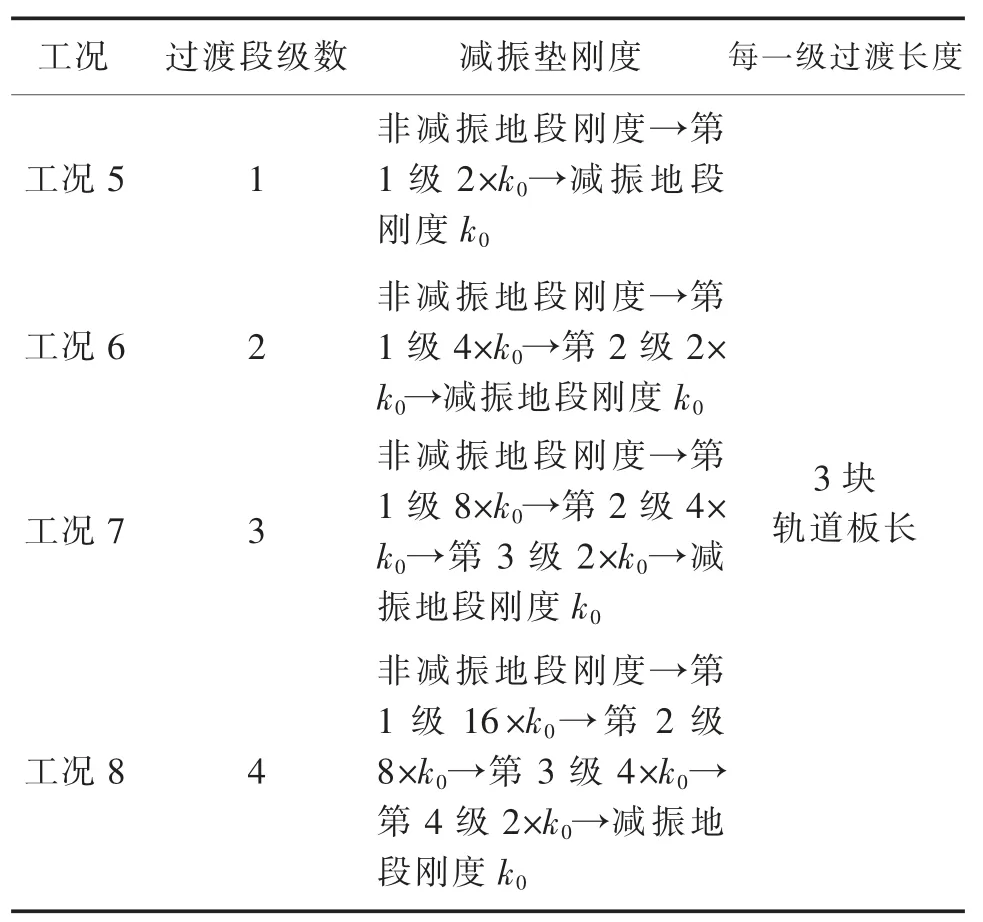
表3 分级过渡措施过渡段级数计算工况Tab.3 Calculation conditions of transition stages of graded transition measures

3 轨道刚度过渡段动力分析

3.1 评价指标

综合考虑车辆和轨道动态响应两方面，对钢轨挠曲变化率、车体加速度、轮轨力、轨道板缝两侧错台量、 轨道板缝两侧扣件下压力等指标进行分析。其中， 钢轨挠曲变化率要求不得大于0.3 mm/m[8]，车体垂向加速度幅值、横向加速度幅值要求不得大于2.5 m/s2，脱轨系数要求不得大于0.8，轮重减载率要求不得大于0.8[16]。

3.2 每一级过渡长度的影响

3.2.1 轮对垂向位移

列车经过过渡段时刻的轮对垂向位移计算结果如图2 所示， 随着过渡段减振垫刚度的逐级降低，垂向位移逐级增大，在经过板缝时出现垂向位移峰值，各级交界面垂向位移突然增大。

图2 4 种工况下过渡段的轮对垂向位移Fig.2 Wheel set vertical displacement of transition section under four working conditions

3.2.2 车体垂向加速度

改变每一级过渡长度，对车体垂向加速度影响显著，如图3 所示。 过渡段范围内工况1、工况2 的加速度幅值大于工况3 和工况4， 其中工况1 的最大。 工况1，2，3 发生在后轮对进入过渡段的时刻附近，工况4 的加速度最大值发生在前轮刚进入减振段的时刻，这是由于工况4 的每一级过渡长度已足够长，当后轮对进入过渡段时，前轮对仍处在该级过渡段， 使得此刻的车体加速度要低于其他工况。车体加速度的多处峰值反映了车轮经过板缝时的冲击作用，尤其在不同级过渡段的连接处，冲击作用更加显著。

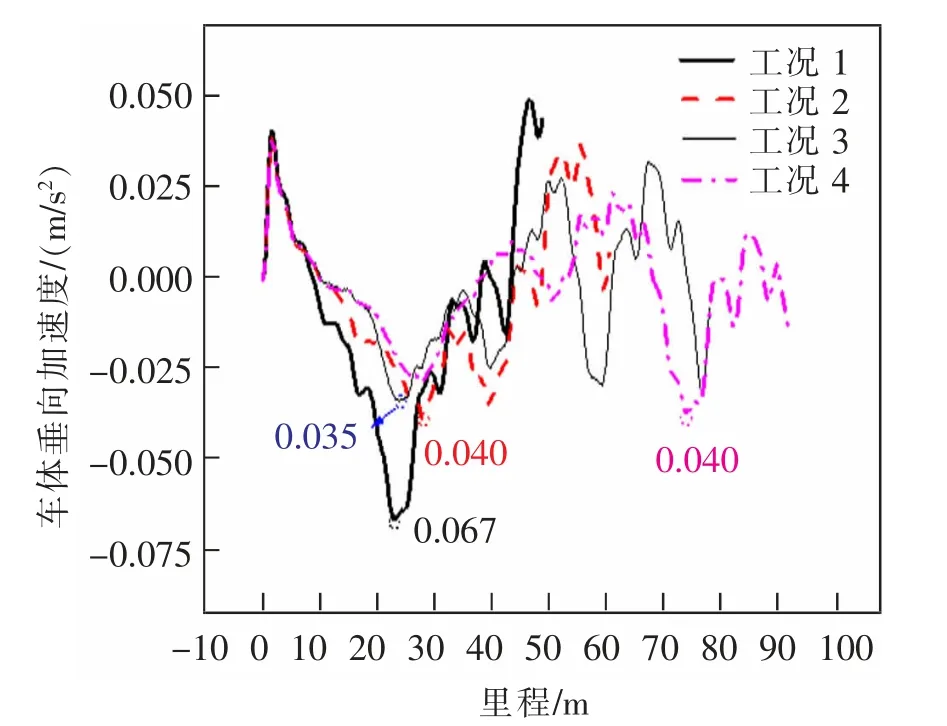
图3 4 种工况下过渡段的垂向加速度Fig.3 Vertical acceleration of transition section under four working conditions

图4 4 种工况下过渡段的垂向轮轨力Fig.4 Vertical wheel rail force of transition section under four working conditions

3.2.3 轮轨力

4 种工况下的前轮垂向轮轨力如图4 所示，图中的虚线方框可以明显看到经过板缝位置时轮轨力的突增。从工况1 到工况3，每一级过渡长度增大，垂向轮轨力幅值减小。 但从工况3 到工况4，继续增大每一级过渡长度，垂向轮轨力幅值反而有所增大。 该结果表明， 就减小列车经过过渡段时的垂向轮轨力而言，每一级过渡长度取3 块轨道板长度比较有益。

3.2.4 轮轨系统动力响应幅值

4 种工况下的轮轨系统动力响应幅值见表4。 在过渡级数不变（3 级），各级过渡段减振垫刚度按双倍递减的情况下，增大每一级过渡长度，从表4 可以得出：

1） 过渡段与减振地段交界面的板缝两侧扣件下压力，当每一级过渡长度从1 块轨道板长增大至3块轨道板长时，差值减小18%。 但当每一级过渡长度达到4 块板长时，该指标较3 块板长反而有所增大。

2） 过渡段范围钢轨挠曲变化率幅值满足不得大于0.3 mm/m 的限值要求。

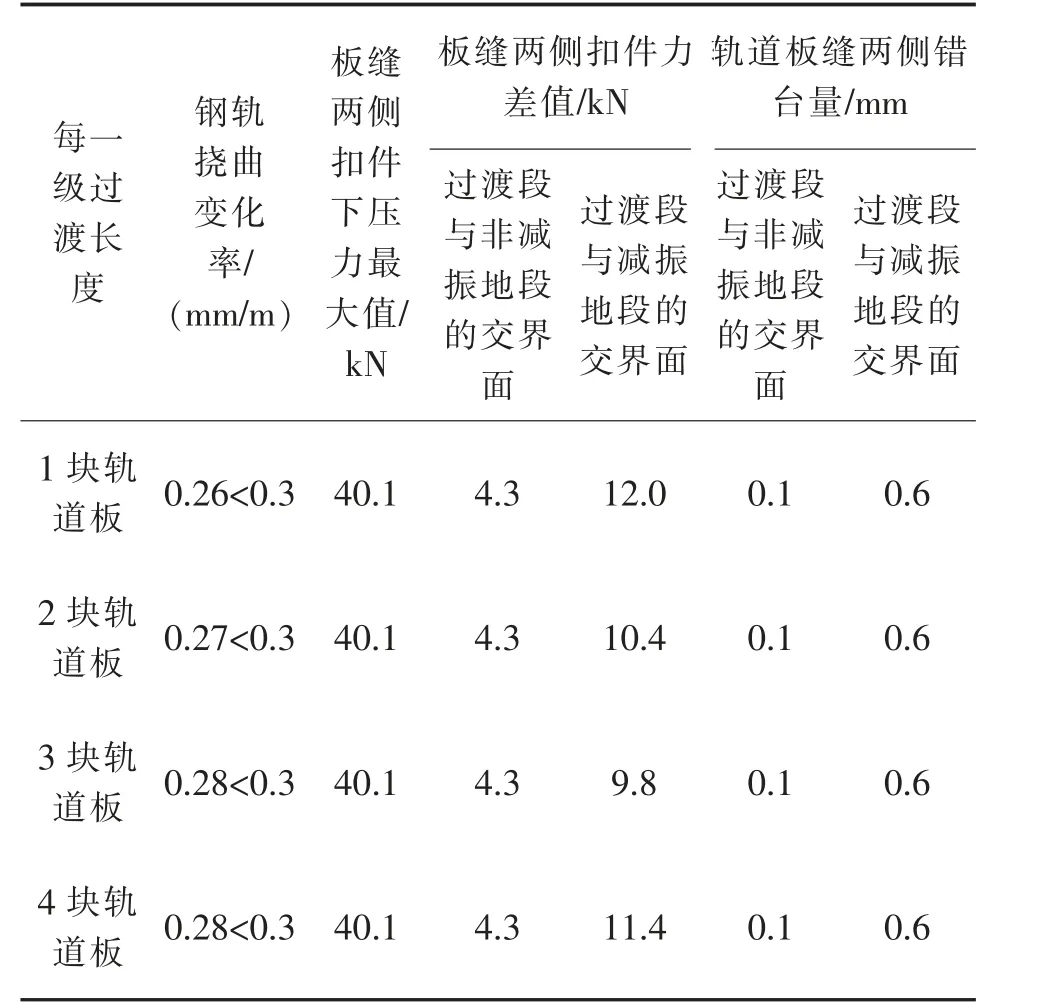
表4 4 种工况下的轮轨系统动力响应幅值Tab.4 Dynamic response amplitude of wheel rail system under four working conditions

3.2.5 列车运行品质及稳定性

考虑轨道不平顺，采用德国低干扰谱，进一步分析列车在4 种工况下的运行品质及稳定性，钢轨表面不平顺如图5 所示，计算结果见表5。当每一级过渡长度为1 块轨道板时运行品质和稳定性最差，但4 种工况均满足限值要求。

表5 4 种工况下的运行品质及稳定性Tab.5 Operation quality and stability under four working conditions

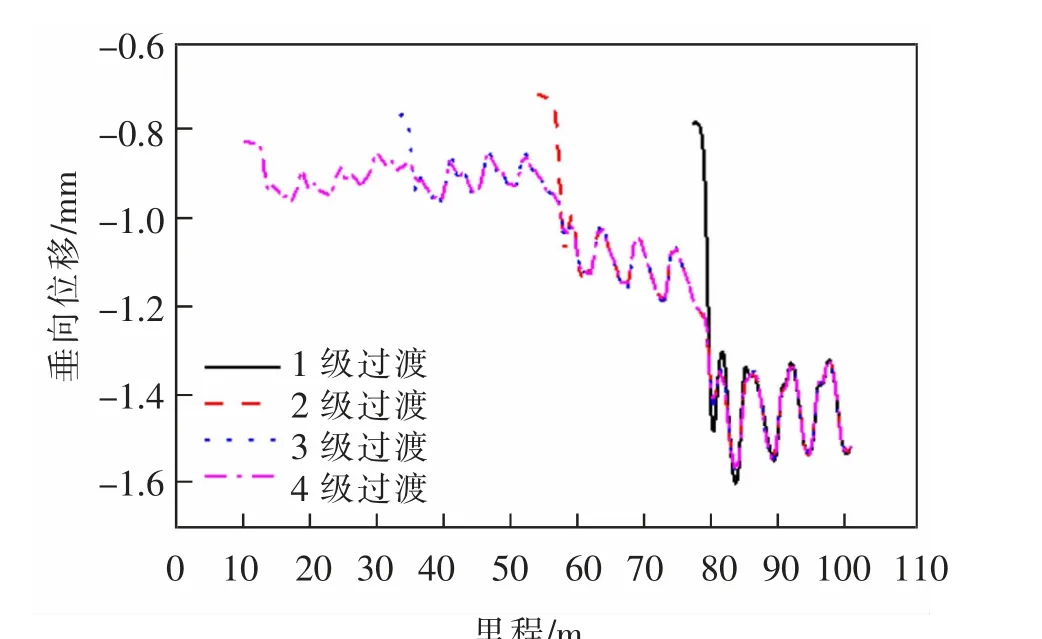
图6 4 种工况下过渡段的轮对垂向位移Fig.6 Vertical displacement of wheelset in transition section under four working conditions

3.3 过渡级数的影响

3.3.1 轮对垂向位移

列车通过过渡段时，过渡级数越多，轮对垂向位移突变值越小。 过渡级数从1 级增加至3 级，垂向位移突变值减小显著，而3 级和4 级垂向位移突变值基本相当，如图6 所示。

3.3.2 车体垂向加速度

图7 为4 种工况下的车体垂向加速度，从整体看，过渡段范围内工况5>工况6>工况7>工况8，即过渡级数越多，车体垂向加速度越小，但车体加速度减小的差值随着过渡级数的增加而降低。 工况5，6，7 的加速度最大值发生在后轮刚进入过渡段的时刻附近，工况8 的加速度最大值发生在前轮刚进入减振段的时刻。 这是由于前3 种工况非减振地段与第1 级过渡段的刚度差异太大，而工况8 的第1级过渡段刚度比较接近非减振地段刚度。

3.3.3 轮轨力

图8 为4 种工况下前轮的垂向轮轨力。 总体看， 轮轨力的多处幅值随着过渡级数的增加有所降低，但当级数增加至4 级时，垂向轮轨力幅值反而比3 级更大。 该结果表明，就减小列车经过过渡段时的垂向轮轨力而言， 过渡级数采用3 级比较有益。

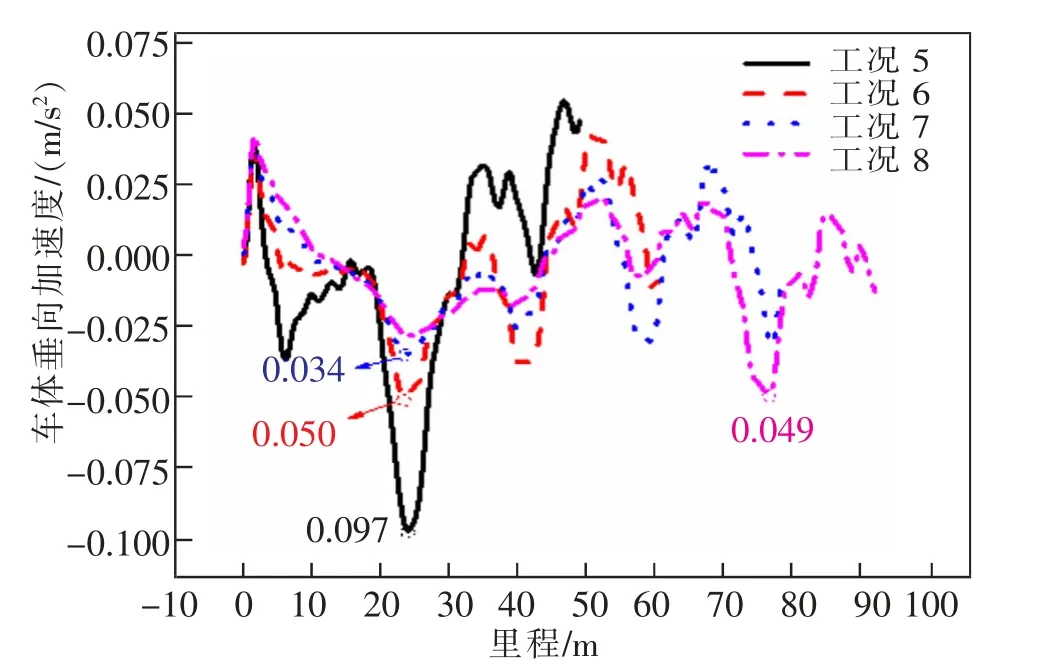
图7 4 种工况下过渡段的垂向加速度Fig.7 Vertical acceleration of transition section under four working conditions

3.3.4 轮轨系统动力响应幅值

在每一级过渡长度一定（3 块轨道板长）的情况下，增加过渡级数，从表6 可以得出：

1） 板缝两侧扣件下压力最大值减小，但当过渡级数为4 级时，较3 级反而有所增大。

2） 过渡级数从1 级增大到3 级，钢轨挠曲变化率幅值减小57%，板缝两侧扣件下压力最大值减小10%， 过渡段与非减振地段交界面的板缝两侧扣件下压力差值减小75%，过渡段与非减振地段交界面的板缝两侧错台量减小83%。

3） 1 级和2 级过渡方式过渡段范围钢轨挠曲变化率幅值不满足小于0.3 mm/m 的限值要求，3 级和4 级过渡方式可满足。

表6 4 种工况下的轮轨系统动力响应幅值Tab.6 Dynamic response amplitude of wheel rail system under four working conditions

3.3.5 列车运行品质及稳定性

考虑轨道不平顺， 进一步分析了列车在不同过渡级数工况下的运行品质及稳定性， 计算结果见表7。 过渡级数为1 级时运行品质最差，过渡级数为2 级时稳定性最差，但均满足限值要求。

表7 4 种工况下的运行品质及稳定性Tab.7 Operation quality and stability under four working conditions

4 结论

针对CRTSⅢ型板式无砟轨道减振地段与非减振地段的刚度过渡，在减振地段减振垫刚度为0.02 N/mm3，各级过渡段减振垫刚度按双倍递减的情况下，分别讨论每一级过渡长度和过渡级数对轮轨动力响应的影响，得出主要结论如下：

1） 当过渡级数一定时， 对比每一级过渡段长度为1 块轨道板、2 块轨道板、3 块轨道板长3 种工况，采用3 块轨道板长轮轨力幅值最小，过渡段与减振地段交界面板缝两侧扣件下压力差值最小，车体垂横向加速度幅值最小，脱轨系数及轮轨减载率最小。 继续增大至4 块轨道板长对减小相关指标值未见显著效果，个别指标反而有所增大。因此，每一级过渡长度建议采用3 块轨道板长，此时钢轨挠曲变化率、 列车运行品质和稳定性满足相关限值要求。

2） 当每一级过渡长度一定时，对比1 级、2 级、3 级过渡3 种工况，采用3 级轮对垂向位移突变值、轮轨力幅值、钢轨挠曲变化率幅值、板缝两侧扣件下压力、过渡段与非减振地段交界面板缝两侧的错台量和扣件下压力差值均最小。 继续增加过渡级数至4 级对减小相关指标值未见显著效果，个别指标反而有所增大。 因此，过渡级数建议采用3 级，此时钢轨挠曲变化率、列车运行品质和稳定性满足相关限值要求。

3） 在过渡段范围内，列车在经过轨道板缝时轮对垂向位移出现显著的峰值，表明在板缝处存在较大的轮轨冲击作用， 尤其在各级过渡段的交界面，轮轨冲击作用更加显著。 建议加强对板缝、各级过渡段交界面附近扣件系统的养护和核查。