柱塞泵组件球面缝隙流动特性分析
陈旭峰, 高文科, 张继铭
(兰州理工大学 能源与动力工程学院, 甘肃 兰州 730050)
引言
缝隙流动普遍存在于液压元件等机械装置,缝隙的大小和结构不仅决定流体介质的速度、压力分布等特性,同时还与整机的工作性能密切相关。在缝隙的结构形式上,可分为平行平板间隙、倾斜平板间隙、圆柱环形间隙、渐缩及渐阔同心环形间隙、渐缩及渐阔偏心环形间隙、平行圆盘间隙、圆锥环形间隙、球面缝隙等。在柱塞泵中,球面缝隙是常见的缝隙结构之一,如在柱塞泵中柱塞球头与滑靴球窝构成的间隙为球面缝隙;在某些球面配流副中,缸体端面和配流盘端面也构成球面缝隙。因此,针对球面缝隙结构分析其结构参数与流体介质流动特性之间的关系,对优化此类球面副的设计显得尤为必要。
针对球面缝隙流动的研究,大多是从实际工程的角度出发,对某一具体结构进行研究,如柱塞泵中的球面配流副等[1-3]。王致清等[4]在考虑形成球面缝隙的两元件有相同半径的条件下,求出了考虑流动惯性时的球面间流体的压力分布、速度分布以及泄漏流量的解析式。许贤良等[5]推导了具有相同半径的球窝与球头形成球面缝隙时,其间隙内流体流动的基本运动方程,并进一步推导了球面缝隙中流体的速度分布及压力分布。阳恩会[6]对具有相同半径的球头与球窝形成球铰副时,推导出了球铰副静态摩擦力矩的计算公式,并对球铰副的支承特性和油膜刚度进行了分析。
针对柱塞泵球面配流副的研究,孟广耀等[7]分析了球面配流与平面配流对柱塞泵的压力流量脉动、空化等方面的影响。李小宁等[8]针对形成球面配流副的缸体端面和配流盘端面有相同的半径时,对球面配流副的径向反推力和反推力矩进行了求解,并得到了解析解。王伟[9]、向伦凯[10]在考虑配流盘球面和缸体球面有相同的半径且其球心具有一定偏心时,对其间隙内流体的速度分布、压力分布、泄漏流量及流体的承载量进行求解,并得出了相应的解析表达式。同时,在球面配流副中泄漏流量是衡量摩擦副润滑效率的主要指标[11-14]。李小金等[15]推导出基于球面坐标系的贴体网格生成方程,在贴体坐标系下利用有限差分法迭代求解雷诺方程,得到了球面配流副的二维稳态压力场。邓海顺等[16]在考虑形成球面配流副的缸体端面和配流盘端面有相同的半径时,提出了球面配流副最佳平均间隙的概念,进一步完善了球面配流副的理论。
在球面配流副的大部分研究中忽略了球面配流的影响并将球面配流副简化为平面配流副[17-20]。同时,关于球面缝隙流动的研究,在结构上大多是考虑形成球面缝隙的两元件有相同的半径且其球心存在一定的偏心时进行分析。但在实际工程中,很难保证形成球面间隙的两元件有相同的半径,如柱塞泵中柱塞球头与滑靴球窝组成的球面缝隙,其通常要求滑靴球窝的半径要略大于柱塞球头的半径,且在运行过程中滑靴球窝的球心相对于柱塞球头的球心会发生一定的偏心。此外,如图1所示,在形成球面缝隙的2个元件的结构的限制下,如果当0<θ1<π/2,π/2<θ2<π,并且2个元件的球心存在一定的偏心时,此时的两元件不可能有相同的半径。因此,文献[5-10]、文献[16]中所提供的结果仅适于计算0<θ1<θ2<π/2时的球面缝隙结构。
基于此,本研究从柱塞泵中所出现的球面缝隙机械结构出发(柱塞球头与滑靴球窝构成的球铰副以及球面配流副),针对形成球面缝隙的两元件存在不相等的半径且球心发生一定的偏心时,对其缝隙中流体的速度分布、压力分布、泄漏流量及流体的承载量进行建模,并以滑靴球窝与柱塞球头构成的球面缝隙为例,分析其缝隙内流体的压力分布、速度分布等特性。
1 缝隙间流体流动相关参数计算
球面缝隙流动常见于各种机械结构,如柱塞泵中的球面配流副,以及滑靴球窝与柱塞球头构成的球铰副等。在不同的机械结构中,流体到达球面缝隙的方式也有所不同。于是,可将各种满足球面缝隙流动的机械结构简化为如图1所示的结构。由图1可知,球A与B之间的球面缝隙中充满了高压油液,油液在高压pr的作用下通过两球面之间的间隙流出到外界(外界压力为p0),A与B均保持静止,并且满足0<θ1<90°,θ1<θ2<180°,其中θ表示密封带相对于竖直方向的张角,其值位于θ1~θ2之间。
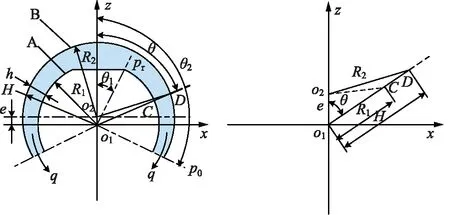
图1 球面缝隙结构示意图
A与B之间的油膜呈球形分布,此时宜采用球坐标系,如图2所示。在球坐标系下,对于黏性不可压缩流体,N-S方程如下:
(1)
式中,fr,fθ,fφ分别为r,θ,φ3个方向的单位质量力,fr=-gcosθ,fθ=gsinθ,fφ=0;ur,uθ,uφ分别为r,θ,φ3个方向的流体运动速度;p,ρ,μ分别为压力、密度、动力黏度;dur/dt,duθ/dt,duφ/dt分别表示r,θ,φ3个方向的流体运动的加速度。

图2 球坐标示意图
对于精确求解N-S方程存在极大的困难。为此,根据球面缝隙流动的特点,其次通过比较各项的数量级,略去方程中的微小量,保留主要项,使得方程得到化简。现将求解N-S方程的假设条件叙述如下:
(1) 油液为牛顿流体,并忽略油液质量力的作用。油液流动为层流,油膜中不存在湍流,与黏性力相比可忽略油液惯性力的作用,包括流体加速时的力和油膜弯曲的离心力;
(2) 油液充满整个球面缝隙,在固体表面上油液无滑动,即贴于固体表面的油液流速与表面速度相同;
(3) 在沿着油膜厚度方向(即r方向)上忽略油液压力的变化,即∂p/∂r=0。由于膜厚仅为百分之几毫米或更小,因此压力不可能发生明显的变化;
(4) 在球面缝隙流动中,uθ为主要的速度分量,其他速度分量uφ=ur=0;
(5) 由于球面缝隙流动关于z轴对称,因此各流动参数与φ无关,即∂/∂φ=0。
基于上述假设,则N-S方程可化简为:

(2)
对式(2)中第一式,可等价化简为:
(3)
于是,将式(3)代入式(2)中第二式,则:
(4)
根据假设(3)及假设(5)可知,p与r,φ均无关,则∂p/∂θ=dp/dθ。对式(4)进行积分,则:
(5)
实际上在工程问题中,形成球面缝隙的A与B很难保持同心,往往存在一定的偏心e。同时,由于存在加工精度及配合等问题,也很难保证A与B有相同的半径,对于A与B的相对位置,如图3所示。
由图3可知,当偏心e>0时,随着θ的增大,油膜厚度逐渐减小,油膜在θ方向上呈渐缩状态;当偏心e=0时,油膜厚度恒为定值;当偏心e<0时,随着θ的增大,油膜厚度逐渐增大,油膜在θ方向上呈渐阔状态。

图3 球面缝隙结构相对位置示意图
如图1所示,在三角形o1o2D中,|o1o2|=e,|o1D|=H,|o2D|=R2,|o1C|=R1,于是根据余弦定理则有:
(6)
于是,解得H为:
(7)
通常e/R2≪1,因此忽略高阶微量,则:
H=R2+ecosθ
(8)
因此,球面缝隙尺寸(或油膜厚度)为:
h=|CD|=H-R1=R2-R1+ecosθ
(9)
令δ=R2-R1,则:
h=δ+ecosθ
(10)
如图1所示,考虑其本身机械结构,即在任意θ处,油膜厚度h均大于0,则当θ=θ1时,h>0;当θ=θ2时,h>0。代入式(10),则半径间隙δ与偏心距e的关系式为:
δ+ecosθ1>0
δ+ecosθ2>0
(11)
根据边界条件(假设(2)),当r=R1时,uθ=0,当r=H时,uθ=0,则解得油液流速uθ为:
(12)
如图2所示,在球坐标系中,在r,θ处的微元面积dA=rsinθdφdr,则流过微元面积dA的微元流量dq为:

R1(R2+ecosθ))sinθdφdr
(13)
对式(13)进行积分得:
(14)
考虑到在微元面积dA处,流速uθ的方向与微元面积dA的外法线方向相反,因此此时计算出的总泄漏流量q为负值。于是,在整个球面缝隙中,流量数值大小为:
Q=-q
(15)
令ε=e/δ,根据式(8),则ε的取值范围为:
1+εcosθ1>0
1+εcosθ2>0
(16)

在柱塞球头与滑靴球窝构成的球铰副中,通常满足0<θ1<π/2且π/2<θ2<π时,此时cosθ1>0且cosθ2<0,则有-secθ1<ε<-secθ2,此时由于机械结构所限,ε既有下确界又有上确界。
于是,将式(11)变换成dp的微分式,并将式(10)代入,则:
(17)
对式(17)进行积分,并代入压力的边界条件,即当θ=θ1时,p=pr;当θ=θ2时,p=p0,则解得压力分布p及流量数值大小Q分别为:

(18)

(19)
令:
(20)
式(20)中,Kq仅与θ1,θ2及ε有关,其中θ1与θ2表示在结构上A与B构成的球面缝隙的尺度大小,ε表示在结构上A与B球心的偏心程度。从而,Kq仅由A与B的几何尺寸以及A与B的相对偏心程度所唯一确定,Kq可称为球面缝隙流动中的球面支撑泄漏系数。
则:
(21)
由球面缝隙中油液压力的表达式,可求得压力对θ的梯度为:
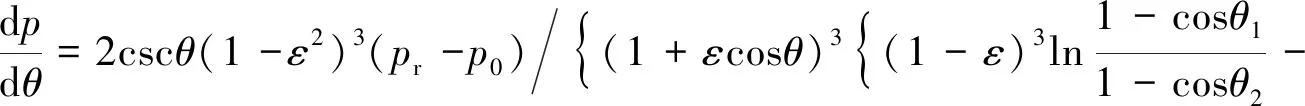
(22)
将式(22)代入式(12),则球面缝隙内油液的速度分布为:
(23)
2 油膜承载量分析
如图2所示,在球A面上微元面积dAp可表示为(图2中r取R1):
(24)
因此,球面缝隙中油液作用于A上微元面积dAp的作用力可表示:
dFp=pdAp
(25)
将dFp分别沿着水平方向及z方向分解,则:
dFr=psinθdAp
(26)
dFz=pcosθdAp
(27)
因此,球面缝隙中油液作用于球A面上的总的作用力(或油膜的承载量)为:
(28)
(29)
由于球面缝隙流动关于z轴对称,因此Fr=0,Fz可进一步表示为:
(30)
将式(18)代入式(30),则:
(31)
式(31)中,相关积分可积得:
(32)
将J1,J2,J3,J4及J5分别代入式(31),则:
(33)
令:
(34)
式(34)中,KF是仅与θ1,θ2及ε有关的结构常数。从而,KF仅由A与B的几何尺寸以及A与B的相对偏心程度所唯一确定,KF可称为球面缝隙流动中的球面支撑承载系数。
则:
Ⅰ:如果当球A与B的半径相等,即R1=R2=R时,此时δ=R2-R1=0,代入式(18)、式(19)、式(23)及式(33),则球面缝隙中油液的压力分布、流量、流速分布以及油膜承载量分别为:
(36)
(37)


(39)
式(36)~式(39)中,须满足0<θ1<θ2<π/2,这是由于当A与B的半径相等时,此时A与B若存在一定的偏心e,则在其结构本身的限制下,θ1与θ2不可能大于π/2。在球面配流副中,通常满足0<θ1<θ2<π/2,因此在粗略计算其相关参数时,可假定A与B的半径相等,进而进行计算。
Ⅱ:如果当球A与B的偏心距e=0时,代入式(18)、式(19)、式(23)及式(33),则球面缝隙中油液的压力分布、流量、流速分布以及油膜承载量分别为:

(40)
(41)
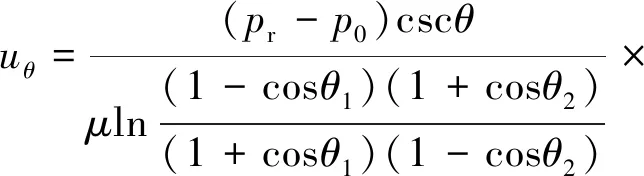
(42)

(43)
在滑靴球窝与柱塞球头构成的球面缝隙中,通常满足0<θ1<π/2且π/2<θ2<π。因此,在粗略计算某些球面缝隙流动相关参数或在某些特殊场合时,可忽略A与B球心的偏心距e,进而进行计算。
3 实例分析
考虑到球面缝隙流动常见于各种机械结构,如柱塞泵中的球面配流副以及滑靴球窝与柱塞球头构成的球铰副等,但在不同的球面副中,其相关参数的计算形式略有差异。因此,本研究仅以滑靴球窝与柱塞球头构成的球铰副进行实例分析。
某型号柱塞泵的滑靴与斜盘摩擦副设计成如图4所示的静压支承。设柱塞阻尼孔直径d=0.4 mm,阻尼孔长度l=25 mm,通过柱塞阻尼孔时压降系数α=pr/ps=0.9;泵的工作压力ps=32 MPa,泵壳内的压力p0=0,油液的动力黏度μ=8.7×10-3Pa·s;柱塞球头半径R1=7.49 mm,滑靴球窝半径R2=7.5 mm,滑靴球头球心相对于滑靴球窝球心的偏心距离e=2 μm,角度θ1=8°,θ2=140°;滑靴底部半径r1=7.5 mm,r2=11 mm;(假设滑靴球窝θ≤θ1范围内的压力与滑靴底部r≤r1范围内的压力相同(即忽略滑靴阻尼孔的压力损失),均为pr)。

图4 柱塞-滑靴示意图
通过柱塞阻尼孔的流量为:
(44)
引入阻尼孔泄漏系数:
(45)
则:
(46)
由式(21),通过滑靴球窝与柱塞球头流出的流量为:
(47)
通过滑靴底部与斜盘间缝隙流出的流量为:
(48)
引入平行圆盘支撑泄漏系数:
(49)
则:
(50)
通过柱塞细长阻尼孔的流量qr一部分通过滑靴自身的阻尼孔到达滑靴底部,另一部分通过滑靴球窝与柱塞球头构成的球面缝隙流出到泵壳内。因此,根据流量的连续性方程,则qr=q1+q2。
代入相关数据,解得Kqr=2.5133×10-14,Kq1=0.1671,Kq2=1.3671。于是,解得通过柱塞细长阻尼孔的流量为qr=554.65 mL/min,通过滑靴球窝与柱塞球头流出的流量为q1=33.18 mL/min,通过滑靴底部与斜盘间的缝隙流出的流量为q2=521.47 mL/min,进而解得滑靴底部与斜盘形成静压支撑的油膜厚度h=12.43 μm。
特殊地,若忽略滑靴球窝相对于柱塞球头的偏心,即假设e=0,则根据式(41),解得通过滑靴球窝与柱塞球头流出的流量为q1=28.33 mL/min,而当偏心距e=2 μm时,q1=33.18 mL/min。因此,此时忽略偏心时所计算的泄漏流量误差为14.62%。
3.1 滑靴球窝内相关参数实例分析
在滑靴球窝与柱塞球头构成的球面缝隙中,仍假设各参数为ps=32 MPa,θ1=8°,θ2=140°,pr=αps=28.8 MPa,R1=7.49 mm,R2=7.5 mm。根据式(21),则ε的取值范围为(-1.0098,1.3054),从而偏心距e的取值范围为(-10.10,13.05)。根据式(10)、式(18)、式(19)以及式(33),绘制出不同ε时,油膜厚度h、压力分布p、流量Q、油膜承载量Fz的函数图像,如图5~图8所示。当偏心距e=2 μm时,根据式(23),绘制出球面缝隙中油液流速uθ随θ及r的函数图像,如图9及图10所示。
由图5可知,当ε<0时,随着ε的增大,油膜厚度h逐渐增大,油膜在θ方向上呈渐阔状态;当ε=0时,油膜厚度h恒为定值,且h=δ;当ε>0时,随着ε的增大,油膜厚度h逐渐减小,油膜在θ方向上呈渐缩状态。
由图6可知,当ε<0时,压力曲线整体位于ε=0
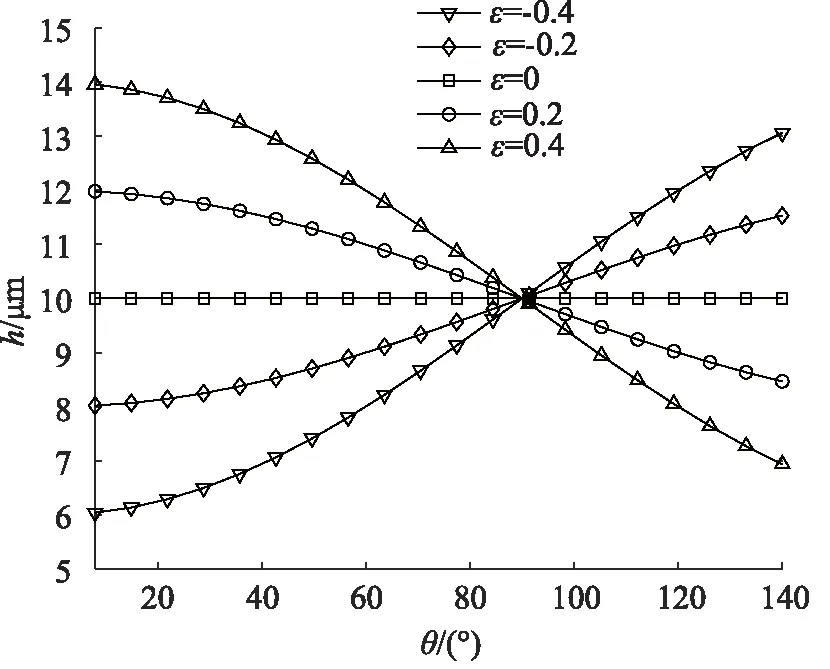
图5 不同ε下的油膜厚度分布

图6 不同ε下的油液压力分布
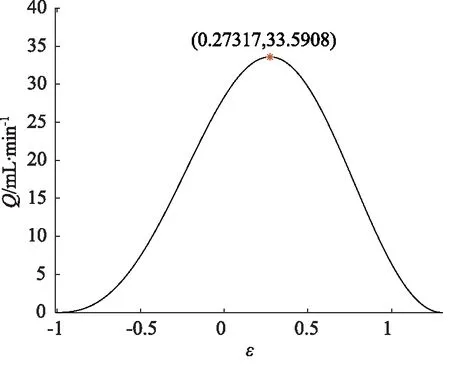
图7 不同ε下的泄漏流量
时的压力曲线下侧;当ε>0时,压力曲线整体位于ε=0时的压力曲线上侧。
由图7可知,随着ε的增大,流量Q先增大后减小,且当ε=0.2732时,流量Q达到最大值Qmax=33.59 mL/min。
由图8可知,随着ε的增大,承载量Fz先增大后减小,且当ε=0.5952时,承载量Fz达到最大值Fz max=3078.37 N。

图8 不同ε下的油膜承载量

图9 流速分布曲面图

图10 流速分布曲线图
由图9、图10可知,当张角θ一定时,球面缝隙中油液流速uθ在油膜厚度方向(即r方向)上呈抛物线分布。
4 结论
(1) 从柱塞泵中所出现的球面缝隙机械结构出发(柱塞球头与滑靴球窝构成的球铰副以及球面配流副),针对形成球面缝隙的两元件存在不相等的半径且球心发生一定的偏心时,对其缝隙中流体的速度分布、压力分布、泄漏流量及流体的承载量进行了求解,并得到了其解析表达式。同时,得到了仅与球面缝隙流动其自身结构有关的球面支撑泄漏系数Kq和球面支撑承载系数KF;
(2) 通过本研究所推导的式(18)、式(19)、式(23)、式(33)可直接导出当两元件存在相等的半径且球心发生一定的偏心时,其缝隙内流体相关参数的表达式,如式(36)~式(39),这与文献[5-10]、文献[16]中所提供的相应结果完全一致。同时,通过式(18)、式(19)、式(23)、式(33)也可推导出当两元件存在不相等的半径且忽略球心的偏心时,其缝隙内流体相关参数的表达式,如式(40)~式(43)所示;
(3) 以滑靴球窝与柱塞球头形成的球铰副为例,对其球面缝隙中油液的速度分布、压力分布、泄漏流量及油膜承载量等进行了求解,并进行了数值分析。对于滑靴球窝与柱塞球头之间泄漏流量的精确求解,可进一步为滑靴底部与斜盘表面间油液的承载量、泄漏流量、油膜刚度等参数的研究提供进一步的参考。
在实际工况中很难保证形成球面缝隙的两元件有相同的半径,因此通过更为精确的求解其缝隙内流体相关参数的分布,可进一步为相关形成球面缝隙的机械结构(如柱塞泵中的球面配流副滑靴球窝与柱塞球头构成的球铰副等)设计提供理论依据。

