基于内积正则化的自表示无监督特征选择算法

武 文， 段雪峰

(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)

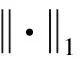
用迹函数表示为‖B‖2,1=tr(BTGB)，其中G为对角矩阵，满足Gii=1/2‖Bi‖2，Bi为矩阵B的第i个行向量。

特征选择按有无标签分为有监督和无监督两类。在实际应用中，大多数数据无标签信息，所以要通过已有的数据对信息进行加工过滤，选择其中有限个特征来组成一个可以代表整个特征空间的特征子集。该子集比原始特征空间的维数低，但具有原始特征空间的特性。越来越多的新技术被引入特征选择算法模型中，如稀疏学习[1]、图正则化[2]、谱聚类[3]、自表示[4]和矩阵分解[5-6],通过增强特征之间的局部结构信息和应用局部结构在特征的表示上，可以有效地提高特征选择的准确率。考虑到l2,1范数的鲁棒性及其可以降低数据的冗余性，鲁棒无监督特征选择方法[5]和自表示特征选择方法[4]使用l2,1范数作为损失函数和正则项。

在信息时代，结构化矩阵的低秩逼近频繁出现在各个领域。对于对称半正定矩阵的低秩逼近问题，白建超等[7]基于矩阵的满秩分解和非负矩阵分解算法构造了一种新的乘性迭代算法。针对对称半正定矩阵的正则化低秩逼近问题，张雪伟等[8]基于对称半正定矩阵的Gramian分解将原问题转化为等价的无约束优化问题，并通过构造非线性共轭梯度方法进行求解。黄琼慧等[9]利用满秩分解来刻画问题的可行集，从而将非负矩阵的正则化逼近问题转化为等价的非负矩阵分解问题，并通过构造交替最小二乘方法进行问题求解。

研究如下问题：

问题1对于一个给定的高维数据矩阵X=[x1,x2,…,xn]T∈Rn×m，特征选择过程可表述为以下无约束优化问题：

(1)

其中Y∈Rn×m为伪标签矩阵。

对于问题1的损失函数，用l2,1范数替代Frobenius范数。正则化项的选择也至关重要，常用的正则项有l0范数、l1范数、l2范数、迹范数、Frobenius范数及核范数。对于正则项，由于内积正则化项最近在许多研究成果中使用且取得良好的聚类效果[10]，用内积正则化项替代l2,1范数。 特征权重矩阵W的内积正则项为

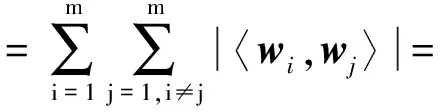
且有

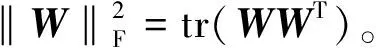
考虑到特征与特征之间的线性非负相关性，即

X=XW+R,W≥0，

其中R为残余矩阵，只有保证‖R‖2,1的值尽可能地小，才能保证特征选择的精确性。

基于以上分析，将问题1重构为如下问题：

问题2对于给定的数据矩阵X∈Rn×m和特征权矩阵W∈Rm×m，W的元素均为非负，特征选择过程可表述为

(2)

1 求解问题2的乘式更新算法

令

F(W)=‖X-XW‖2,1+λΩ(W)=

‖X-XW‖2,1+λ(tr(EWWT)-tr(WWT)),

(3)

对于非负约束W≥0,引入拉格朗日乘子矩阵α∈Rm×m，则式(2)的拉格朗日函数为

L(W)=‖X-XW‖2,1+λΩ(W)-tr(αW)=

tr(X-XW)TP(X-XW)+λ(tr(EWWT)-

tr(WWT))-tr(αW)，

其中P为对角矩阵，且

根据矩阵迹函数对矩阵求导法则，可得

根据KKT条件αijWij=0，可得W的乘式更新表达式：

(4)

算法1内积正则化自表示特征选择算法

输入：X∈Rn×m，k为特征选择的个数，平衡参数λ>0，t为迭代次数，δ>0为充分小的正数。

输出：被选择的特征的指标集{Zx1,Zx2,…,Zxk}。

1.初始化W，且记W=[w1,w2,…,wm]T；

2.开始循环；

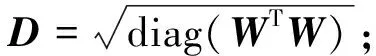
4.按式(4)更新W，

5.当满足收敛标准时，停止循环；

6.求出‖wi‖2,i=1,2,…,m，按降序排列并选择前k个特征，输出对应的指标集。

定义1若以下2个条件同时成立：

1)Φ(u,v)>Ψ(u)；

2)Φ(u,u)=Ψ(u)。

则Φ(u,v)是Ψ(u)的辅助函数。

引理1若Φ是Ψ的辅助函数，则Ψ在如下更新法则下是一个单调递减函数：

其中t为迭代次数。

证明由更新法则

可得

Φ(u(t+1),u(t))≤Φ(u(t),u(t))，

又已知Φ是Ψ的辅助函数，则有

Ψ(u(t+1))≤Φ(u(t+1),u(t))≤

Φ(u(t),u(t))=Ψ(u(t)),

即Ψ是一个单调递减函数，证毕。

引理2函数

是Ψij(Wij)的辅助函数。

证明令式(3)中关于W的函数为Ψ(W)，则

Ψ(W)=-2tr(XTPXW)+tr(WTXTPXW)+

λ(tr(EWWT)-tr(WWT))。

对Ψij关于Wij求导，得

Ψij(Wij)=(-2XTPX+2WXTPX+2λEW-2λW)ij,

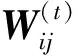
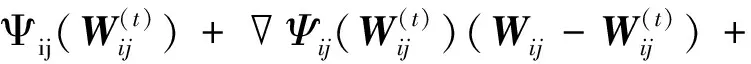
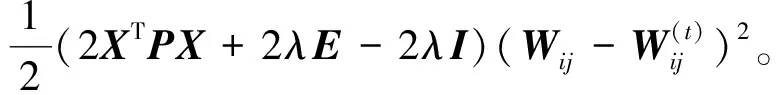
(5)

根据矩阵乘法的运算法则，有以下2个不等式成立：

故显然有式(5)成立。因此，

Φij(Wij,Wij(t))≥Ψij(Wij)，

且

Φij(Wij,Wij)=Ψij(Wij)

成立。由定义1知，Φij(Wij,Wij(t))是Ψij(Wij)的辅助函数。

定理1由算法1产生的迭代序列收敛于问题2的解。

证明由引理2可得，Ψ(W)是一个单调函数，进而F(W)也是单调函数且有界，故其一定是收敛的，即存在一个W*，使得

所以收敛点W*即为问题(2)的解。

2 数值实验

用4个国际标准数据集验证算法1的可行性和有效性。所有实验在MATLAB R2014a环境下进行，其中相对误差的计算式为

数值实验的停机标准为ε(t)<10-4，数据集描述如表1所示。

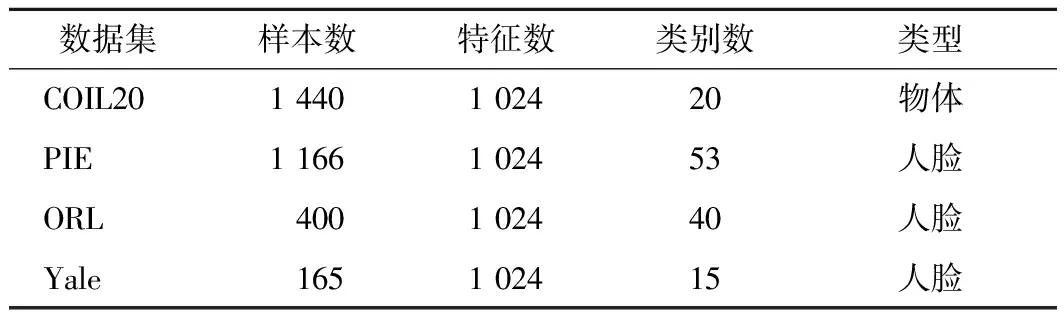
表1 数据集描述

2.1 数据集

选取的4个国际标准数据集如下。

1)COIL20数据集，包含20个不同类别的物体，将每个物体放在一个转盘上，每隔5°进行一次拍照，共1 440张图片。

2)PIE数据集，包括53个不同的人，每人在不同光线条件下以不同的姿势和表情拍摄22张人脸图片，共1 166张。

3)ORL数据集，包括40个不同的人，每人对应10张不同面部表情的人脸图片，共400张。

4)Yale数据集，包含15个不同的人，每人拍摄11张不同光线、动作和神情的人脸图片，共165张。

2.2 对比算法

选取3种特征选择算法作为对比算法，分别为最大方差法[12]、拉普拉斯得分法[11]和正则判别信息特征选择法[13]。

最大方差法MaxVar直接对原特征矩阵计算每个特征的方差，选出方差最大的前k个特征。拉普拉斯得分法Lapscore[11]利用原始特征建立邻接图，通过邻接矩阵和度矩阵得到拉普拉斯矩阵，从而计算出每个特征的拉普拉斯得分，然后选出得分最高的前k个特征。正则判别信息特征选择方法UDFS通过数据的局部判别信息和特征的相关性选择最有区别性的特征，通过计算局部散度矩阵和类间散度矩阵，利用线性分类器将每个样本映射到一个低维空间，并用一个l2,1范数正则化项进行特征选择，得到的稀疏系数矩阵按照其行向量的l2范数值的排名选出排名靠前的数据特征。

2.3 评价标准

对于不同算法选出来的特征子集，经过K均值聚类后可得到聚类标签，通过聚类标签与原标签可计算特征选择的准确率(RACC) 和标准互信息(VNMI)的值，它们的值介于0与1之间，值越高，说明聚类效果越好，即所选出来的特征子集越具代表性。设si为聚类后得到的标签，ti为真正的标签，则

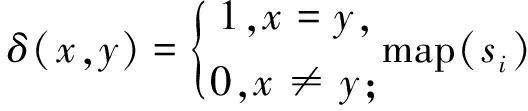
对于给定的2个变量P、Q，VNMI的计算式为

其中：I(P,Q)为P和Q的互信息值；H(P)和H(Q)分别为P和Q的熵。

2.4 参数选择

正则系数λ选自集合{10-4,10-2,1,102,104}。被选择的特征数k选自集合{20,40,60,…,200}，最大迭代次数设置为300。固定λ=100,充分小的正数δ=10-4。

2.5 数值结果分析

图1为算法1在4个数据集上进行特征选择后得到的相对误差变化曲线。从图1可看出，当应用算法1对数据集进行特征选择时，经过数次迭代就可以使相对误差达到充分小且稳定的状态，这表明算法是收敛且有效的。

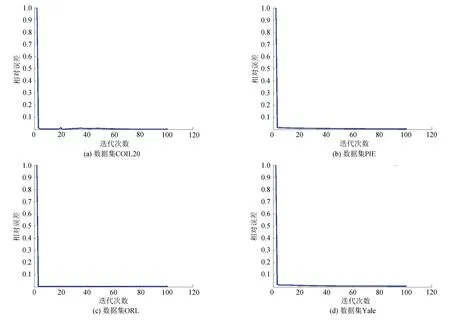
图1 算法1在数据集上的相对误差变化曲线

表2、3为不同算法在不同数据集上通过K均值聚类[14]后得到的准确率与标准互信息的值。每种算法在每个数据集上选择不同数目的特征，使得所选特征的个数遍历指标集{20,40,…,180,200}，然后求出选择不同特征数之后得到的准确率的平均值与标准互信息的平均值。从表2、3可看出，与最大方差法、拉普拉斯得分法和正则判别信息特征选择法相比，算法1的准确率更高，标准互信息值也最高，从而说明该特征选择方法是有效且可行的。

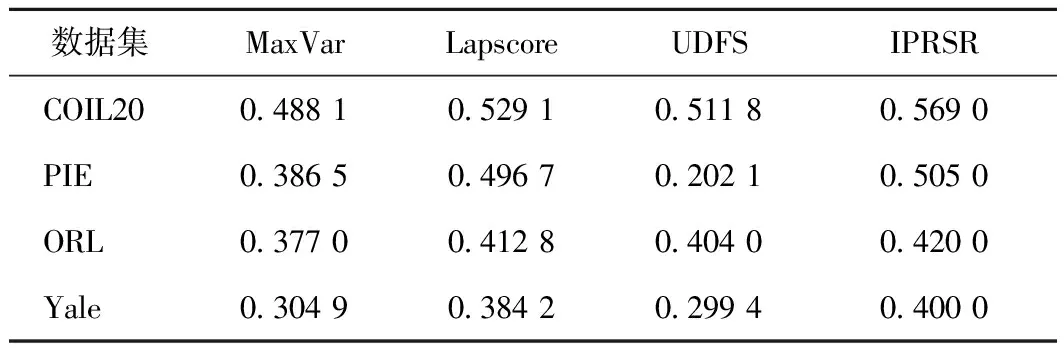
表2 不同算法的准确率

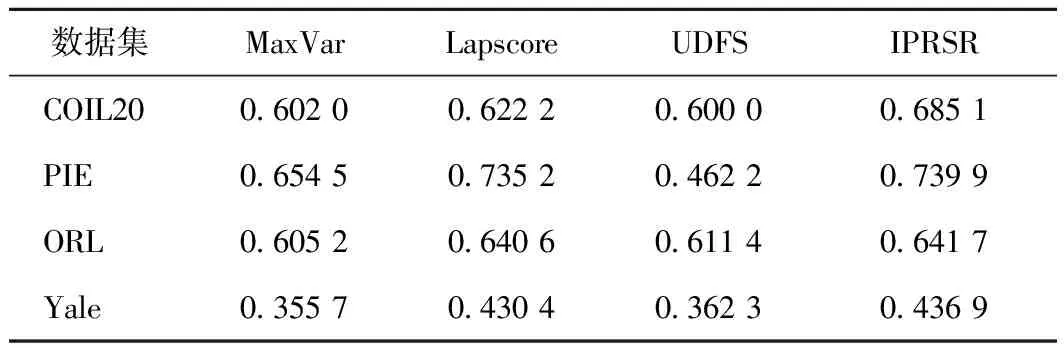
表3 不同算法的标准互信息值

3 结束语

提出了一种用l2,1范数自表示作为损失函数并与内积正则化项相结合的无监督特征选择算法，利用l2,1范数、内积正则化项与迹函数的关系将目标函数转换为可以求导的迹函数形式，并用拉格朗日乘子法对问题进行优化求解。数值实验结果表明，该算法对于特征选择是可行且有效的。