非负象限权互补问题的免导数非单调光滑牛顿法

刘文丽， 迟晓妮,2,3， 张 璐， 李绍刚

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004;2.桂林电子科技大学 广西自动检测技术与仪器重点实验室，广西 桂林 541004;3.桂林电子科技大学 广西密码学与信息安全重点实验室，广西 桂林 541004)

非负象限权互补问题(wCP)定义为寻找一组向量(x,s)∈Rn×Rn，使得

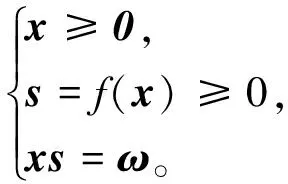
(1)

其中xs=(x1s1,x2s2,…,xnsn)T∈Rn,ω≥0为给定权向量,f(x):Rn→Rn是连续可微函数。若f(x)为线性函数,则对应的权互补问题是非负象限线性权互补问题,否则为非负象限非线性权互补问题。由式(1)知,当权向量ω=0时,wCP退化为互补问题(CP)。

wCP最早由Potra[1]提出。该问题在金融、大气、化学等领域有着重要应用,如Fisher市场均衡问题[1]及线性规划与加权中心问题[2]等皆可通过建立权互补问题来求解。虽然带有非零权向量的wCP比一般的CP理论更加复杂,但wCP模型在某些情况下会提供一个更有效的数值解法。目前关于wCP理论和算法研究已取得了一定的成果。Potra[1]提出了求解非负象限上单调线性wCP的2种内点算法,并建立了算法的计算复杂度。2019年,Gowda[3]研究了欧几里得约当代数上线性wCP和内点系统的共正线性变换。张睿婕等[4]给出一种求解线性wCP的全牛顿步可行内点算法,定义了迭代点到中心路径的邻近测度,并证明了算法具有多项式时间迭代复杂度。

光滑牛顿法因其理论上良好的收敛性,被广泛用于CP的求解[5-8],因此利用光滑牛顿法求解wCP引起了众多学者关注。Zhang[9]运用光滑牛顿法求解单调线性wCP,证明了在适当假设下算法是局部二次收敛的。Tang[10]给出求解线性wCP的光滑方法,并在非严格互补条件下分析了算法的全局和局部二次收敛性。迟晓妮等[11]研究了求解二阶锥wCP的光滑牛顿法,证明了算法的全局和局部超线性收敛性质。

针对非线性方程组问题,Griewank[12]最先提出免导数搜索技术,该搜索技术使得算法不依赖于目标函数的雅可比矩阵，但当目标函数的范数和目标函数正交时,该搜索技术可能会搜索失败,因此Li等[13]给出了新的免导数搜索技术。免导数搜索技术被用于各类优化问题的求解[14-16]。最近，Tang等[17]研究了求解圆锥非线性互补问题的光滑牛顿法,采用新的免导数非单调线搜索技术，确保了其全局和局部超线性收敛性和二次收敛性。

基于此，构造一个新的权互补光滑函数,并分析其性质,然后基于该函数将式(1)转化为光滑方程组。结合文献[13,17-18]的算法思想,提出求解该方程新的免导数非单调光滑牛顿法，在一定条件下证明算法的全局收敛性,并通过数值算例验证算法的有效性。

1 光滑函数及其性质

给定权向量ω≥0,构造式(1)的一个新光滑函数Φ(μ,a,b):R×R×R→R:

(2)

其中α≥0为实参数。若ω=0,易证Φ(μ,a,b)退化为CP的光滑函数

若α=0,则Φ(μ,a,b)退化为Chen-Harker-Kanzow-Smale权互补光滑函数[10]

命题1对任意ω,α≥0,函数Φ(μ,a,b)满足如下性质。

1)Φ(0,a,b)是权互补函数,即

Φ(0,a,b)=0⟺a、b≥0,ab=ω,

(3)

2)Φ(μ,a,b)处处连续可微,强半光滑,且若(a,b)≠(0,0),

否则

aΦ(μ,a,b)=bΦ(μ,a,b)=0,

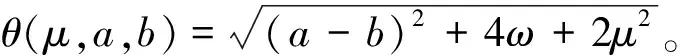
证明由函数Φ(μ,a,b)的定义和引理5.1[19]知，Φ(μ,a,b)连续可微且强半光滑,结合导数链式法则可得2)成立。以下证明1)成立。

1)必要性显然成立。设Φ(0,a,b)=0,根据a不同取值分情况讨论。

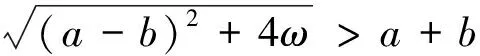
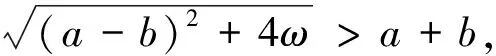
即ab=ω,这与假设ab-ω<0矛盾,因而该种情况不存在；若ab-ω>0,有

即

4(ab-ω)。

因ab-ω>0，则

(4)

由α的任意性知式(4)不成立,故该种情况不存在.

综上所述,Φ(0,a,b)=0，当且仅当a,b≥0且ab=ω成立。证毕。

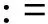
(5)

由式(1)～(3)式知，z*=(μ*,x*,s*)是G(z)=0的解当且仅当(0,x*,s*)是非负象限上wCP(1)的解。

定义1[20]P0矩阵和P0函数定义如下：

1)若矩阵N∈Rn×n的所有主子式非负,则N为P0矩阵。

2)设函数F∶Rn→Rn,对任意x,y∈Rn且x≠y,存在指标i0∈{1,2,…,n}，使得

xi0≠yi0,(xi0-yi0)(Fi0(x)-Fi0(y))≥0

成立,则称F为P0函数。

引理1[20]设F:Rn→Rn是连续可微函数,则对任意x∈Rn,F(x)是P0矩阵当且仅当F是P0函数。

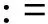
定理1若G(z)如式(5)定义,则以下结论成立。

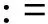
(6)

其中：

(7)

(8)

i=1,2,…,n。

2)设函数f连续可微且单调,则G(z)在任意点z(μ,x,s)∈R++×Rn×Rn处非奇异。

证明由命题1式(2)得式(1)成立。由于f为单调函数,由定义1式(2)和引理1知，f(x)为P0矩阵,又因D2和D3为负对角矩阵,则对任意μ>0,

是非奇异的。证毕。

2 免导数非单调光滑牛顿法

定义

算法1非负象限wCP的免导数非单调光滑牛顿法

3)解以下方程组，得搜索方向

G(zk)+G(zk)Δzk=0。

(9)

4)令λk=δmk,mk为满足

(10)

的最小非负整数，其中：

Qk+1=ηkQk+1；

(11)

(12)

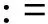
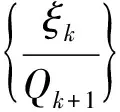
成立。

引理3[21]对任意μ>0,有

引理4设{μk}为算法1生成的迭代序列，则对任意k,有μk≥0,且{μk}为递减序列。

证明由式(9)知，

(13)

假设μk>0,由引理1和式(13)，对任意λk∈(0,1]有

μk+1=μk+λkΔμk≥(1-λk)μk≥0。

又因μ0>0,故μk≥0。再由式(13)得Δμk=e-μk-1≤0,从而

μk+1=μk+λkΔμk≤μk+λk(e-μk-1)≤μk。

证毕。

引理5若函数f连续可微且单调,则算法1适定，且对任意k≥0有H(zk)≤Ck成立。

证明由定理1和引理4知，G(z)非奇异,故步2)适定。假设对任意k有H(zk)≤Ck成立,将式(11)、(12)代入式(10)得

(14)

则步3适定。由步3)得

(15)

根据式(12)、(15)有

(16)

从而结合式(16)和H(z0)=C0得H(zk)≤Ck。证毕。

引理6设{zk}是算法1生成的迭代数列,则{zk}包含于如下水平集中：

证明由式(10)、(16)知，

(17)

由引理2[13]可得

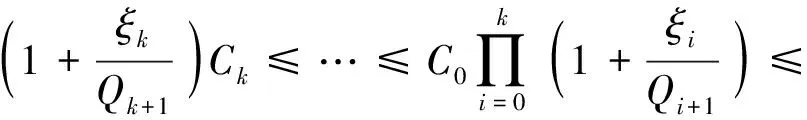
(18)

从而结合式(17)、(18)得H(zk+1)≤eξH(z0),且显然H(z0)≤eξH(z0)。证毕。

3 收敛性分析

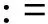
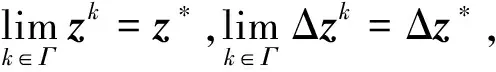
G(z*)+G(z*)Δz*=0。

(19)

因对任意k≥0有λk≥0,故考虑以下2种情况：

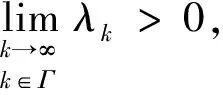
G(z*)=0。

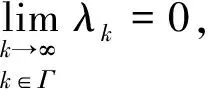
根据引理5得

即

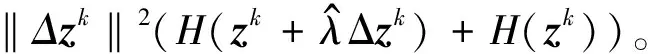
(20)

对式(20)两边取极限得

2G(z*)TG(z*)Δz*≥0。

结合式(19)有

0≤G(z*)TG(z*)Δz*=-‖G(z*)‖2≤0,

即G(z*)=0。证毕。

4 数值算例

运用MATLAB R2014在Intel(R) core(TM) i5-5200 CPU 2.7 GHz 4.0 GiB内存,Windows 7操作系统的计算机上编程。每个算例均以G(z)≤10-8为算法终止条件,且σ=0.05,μ0=0.01,δ=0.5,ξk=2-k。

例1对于wCP式(1),令f(x)=Mx+q,即考虑如下线性非负象限权互补问题：

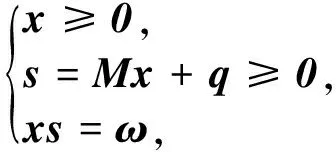
其中M为P0矩阵,向量q∈Rn。

随机生成向量q∈Rn和矩阵N∈Rn×n,定义M=NTN，x*=5×rand(n,1),s*=Mx*+q，ω*=x*s*。选取初始点x0=rand(n,1),设s0=Mx0+q。问题规模n为100～600,取参数ηk=1/2k+1,且随机生成10个问题进行求解。算法1求解不同规模的线性wCP的数值结果如表1所示，其中AIT为平均迭代次数,ACPU为平均CPU时间，AOBJ为算法终止时的平均值。

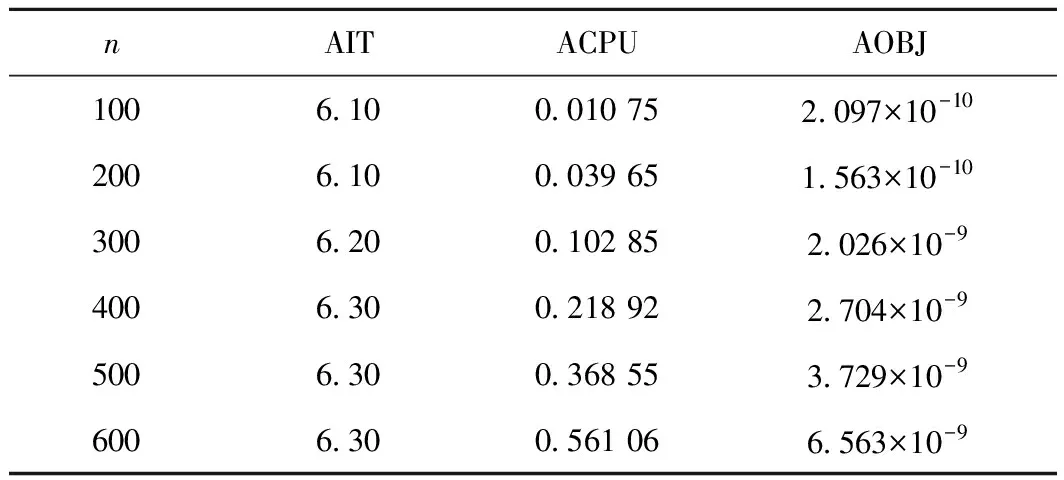
表1 算法1求解不同规模的线性wCP的数值结果

由表1可知,算法1可有效求解非负象限线性wCP,且所需的迭代次数较少,时间较短,因而算法性能高效稳定。

例2考虑非负象限非线性权互补问题：

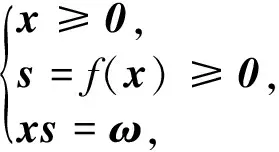
其中f∶R4→R4为连续可微单调函数,定义

实验所需数据按以下方式生成：生成向量x*=rand(n,1),令s*=f(x*)和ω*=x*s*。选取初始点x0=rand(n,1)，s0=f(x0),令控制非单调搜索程度的参数ηk分别取1/2k+1,1/3k+1,1/4k+1,1/5k+1,数值结果如表2所示，其中AOBJ为算法终止时的值。

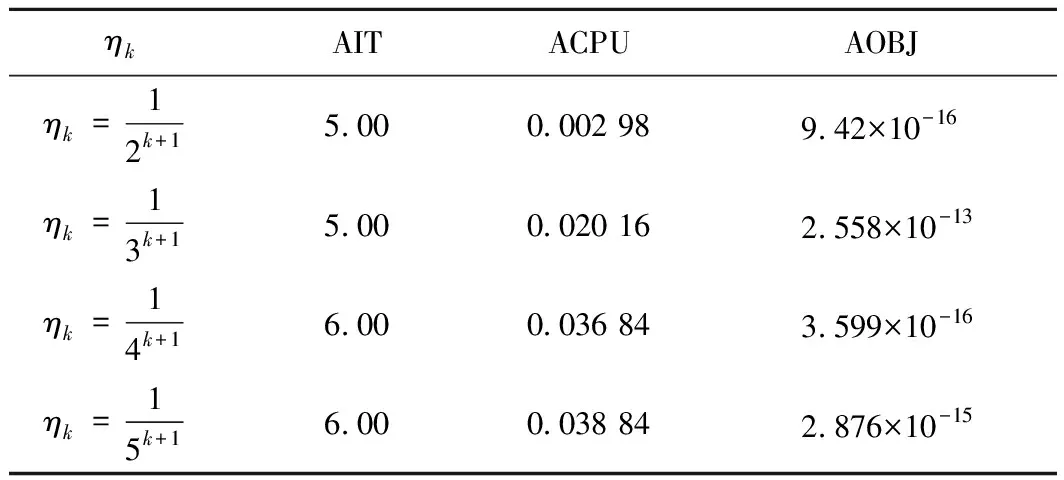
表2 算法1求解不同ηk的非线性wCP的数值结果

由表2可知,算法1能够有效求解非负象限非线性wCP问题,收敛速度快，且迭代次数少。

5 结束语

针对非负象限权互补问题,提出一种免导数的非单调光滑牛顿法，并证明了算法的适定性及收敛性,数值算例表明了算法的可行性和有效性。如何证明本算法的局部收敛性和利用算法解决Fisher市场均衡问题等实际问题，可作为进一步研究的内容。