基于多域特征提取和深度学习的声源被动测距∗

肖旭 王同 王文博 苏林 马力 任群言

(1 中国科学院水声环境特性重点实验室 北京 100190)

(2 中国科学院声学研究所 北京 100190)

(3 中国科学院大学 北京 100049)

0 引言

声源被动测距作为声呐系统的重要功能之一，一直是水声工作者密切关注的问题[1]。由于水声观测信号受复杂的时、空、频变及强多途、高噪声和多普勒效应等因素影响，传统的匹配场处理方法往往面临计算量大和环境失配等问题。近年来，深度学习作为基于数据驱动方式的新兴分支，以其强大的特征提取能力和高效处理复杂、高维、非线性系统问题的独特优势[2]，为水声被动测距提供了一种新思路。

深度神经网络通过大量数据样本建立高维参数之间的复杂非线性映射，适用于物理建模困难的问题，引发了水声研究者的关注。Lefort等[3]通过水箱实验研究了机器学习算法在水声目标测距中的测距性能。Niu等[4]利用单水听器和残差卷积神经网络对声源进行定位。Wang等[5]提出了一种用于水下声源测距的深度迁移学习方法，将从仿真环境获得的预测能力迁移到实验海域。

水声接收信号包含声源和声信道的大量信息，其特征提取和构造是深度学习方法的关键环节。早期特征提取通常利用信号的自相关函数和功率谱估计，或采用时-频分析方法来提取一些时频联合域特征，如短时傅里叶变换(Short-time Fourier transform,STFT)、Wingner-Ville分布等。然而，无论是功率谱分析还是时频分析[6]，它们包含大量与声源位置不相关的信息或冗余信息，在形式上维数较大，一般无法直接应用于测距任务。而且，单一地采用某类特征通常会丢失掉部分特征，缺乏全面性。

针对以上问题，本文设计了一种基于多域特征提取和深度学习的方法来实现声源被动测距。首先从声信号中提取多域特征，包含时域波形结构特征、时域包络特征、频域谱特征和基于STFT的时频联合域特征。然后基于不同谱表达计算出一组声学参数构成特征空间，在此基础上采用最大相关-最小冗余准则(Maximum relevance and minimum redundancy,mRMR)选择特征空间中重要度高的关键特征(与声源位置相关性大)作为模型输入，最后通过一种改进的深度神经网络实现声源距离的估计。神经网络训练时采用自适应矩估计(Adaptive moment estimation,Adam)优化算法和均方误差(Mean squared error,MSE)代价函数进行更新模型参数，用L2和Dropout正则化策略实现网络参数正则化。通过浅海环境仿真实例验证了该方法的有效性，对比分析了波形参数对测距性能和模型收敛速度的影响。

1 理论模型

1.1 水声信号多域特征提取

声信号的多域特征可归纳为6类：时域波形结构特征、时域包络特征、频域谱特征、基于STFT的时频联合域特征、基于等效矩形带宽的听觉谱特征和基于正弦谐波模型的谐波谱特征[7]。每一类特征均包含了对应谱的多种声音特性，这些特征属性无法用单一尺度进行描述，只有在多维特征空间下才能表示。Peeters等[8]对这些声学特征进行总结，并通过多维标度法提取了合适的声学参数，使之与声信号在每个维度上的坐标呈现较大的相关性。

这些声学参数是基于不同谱表达计算的，其表征的物理含义各有不同，而水下声源物理特征和声场信息主要包含在信号的时域波形、频域能量分布中。因此，本文综合了以上更符合水声信号特点的前4类特征，并将所对应的特征归纳为时域特征和时频联合域特征。

1.1.1 时域特征

水声信号时域波形反映了信道对声信号传播的畸变作用，是获取声源总体特征最直接的来源。为了直接从时域提取特征，自相关系数是一种广泛使用的分类特征。首先是对原始信号s(tn)求自相关系数，tn代表信号时刻，保留前N维的自相关系数(c∈{1,···,N})表示为[9]

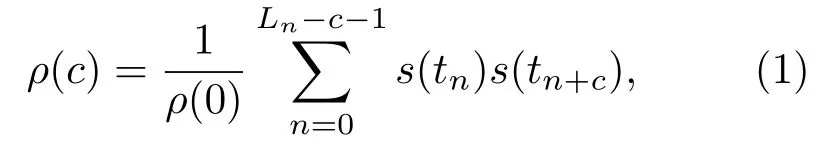
其中，Ln是分帧时的窗长，c代表时间的滞后量。当声源信号为瞬态声信号时，其随时间变化经历ADSR过程，即激励阶段、衰减阶段、稳态持续阶段、释音残响阶段，如图1所示，其中激励阶段到衰减阶段以信号振幅峰值处为分界点，后三阶段统称为下降阶段。

图1 声信号ADSR过程Fig.1 ASDR process of sound signals

声源时域信号的幅度强弱变化和接收距离的相关性较强，为提取描述声源信号幅度变化的特征，对原始信号s(tn)进行Hilbert变换，然后使用截止频率为5 Hz的三阶Butterworth滤波器对振幅信号进行低通滤波，得到信号振幅包络e(tn)。估计信号的起始时间tst、激励阶段和下降阶段的终止时间tAend、tDend，在此基础上定义时域的7个声学参数，如表1所示。其中，为了估计激励过程的时间长度，定义对数激励时间为[10]

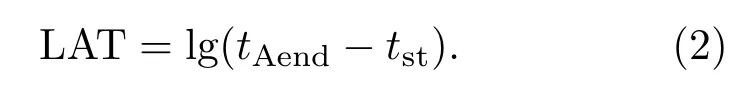
相对应地，将激励阶段和下降阶段能量的平均时间斜率分别定义为激励斜率和下降斜率。估计振幅包络的最大值emax。时间质心给出了信号能量质心所在的时刻，其定义式为[11]

其中，n1和n2为声信号的起始和终止时间对应的索引号，以滤除前后的空白时间。当信号声能量大于一定阈值γemax时，其持续时间定义为信号的有效时间，根据许多经验性的测试，γ取0.4性能较稳定，见文献[8]。除以上参数外，其余参数的公式定义可在文献[8]中一一得到。这些声学参数反映了声源的各种物理属性，例如对数激励时间反映了能量在上升过程中的时间长度，其与声源距离呈正相关，声源距离越远，声信号需达到稳态振动的时间越长。与波形包络相关的特征(激励时间、时域质心等)仅适用于瞬态信号，分析连续声信号时，应提取自相关系数、载波信号调制和后文定义的频域特征。

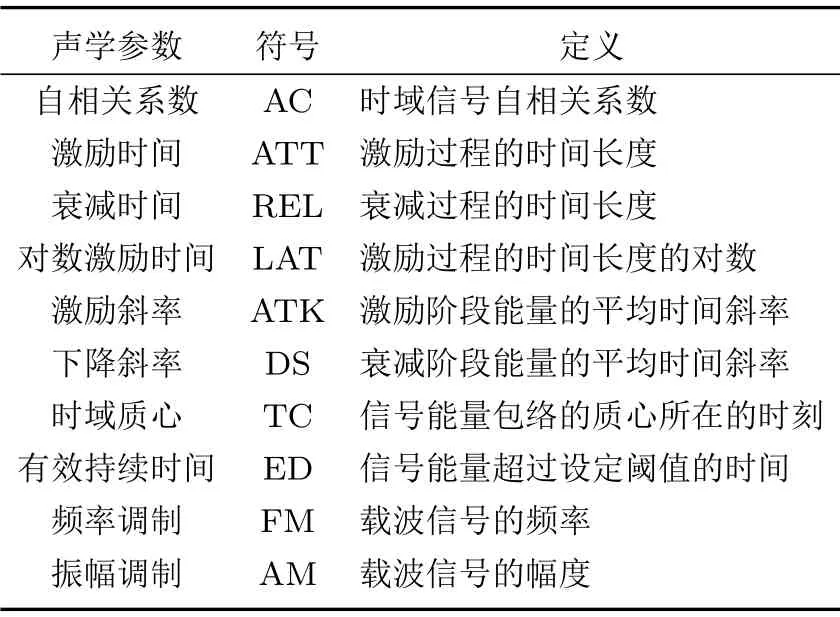
表1 时域特征Table 1 Temp oral features

1.1.2 时频联合域特征

对原始信号进行STFT，把每一帧进行快速傅里叶变换后的频域信号在时间上堆叠起来得到时频谱ak(tm)，其中m代表帧数，k代表频点数。对ak(tm)进行标准化处理：

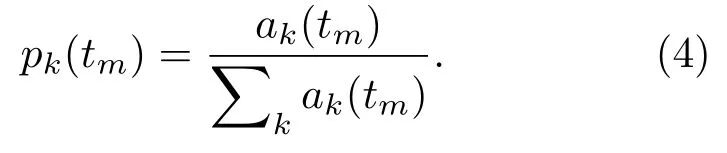
令第k个频点的频率为fk，得到谱的前四阶统计矩，分别定义为谱质心、谱延展、谱斜度和谱峰度[12]，对于第m帧的频谱，表示为

除了频谱的统计特征，根据频谱的斜率特征可以从STFT能量谱中提取谱斜率、谱衰减[8]、谱滚降[13]、谱通量[14]。最后根据线谱特征提取信号的平坦度及谱峰度[8]，其定义和物理含义如表2所示。对于第m帧，上述物理量计算公式分别为

其中，∆f为信号STFT后两点的频率差，fmax为奈奎斯特采样决定的最高频率，是令ak(tm)最大的k(tm)的值。以上参数被证实对声信号的特征识别具有重要作用[15]，被试信号对于它们的变化具有较高的敏感度。

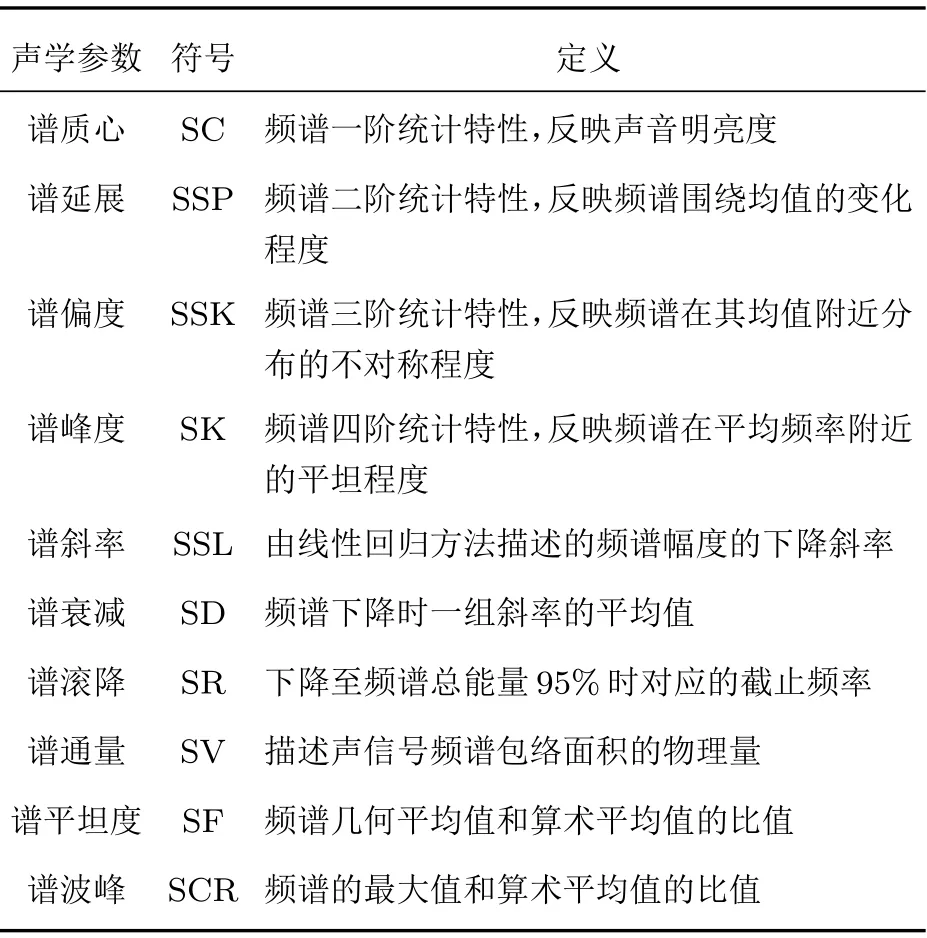
表2 时频联合域特征Table 2 Temp oral-frequency features

1.2 基于mRMR准则的特征选择

以上声学参数作为水声信号的输入特征并不具有鲁棒性，不同任务(如测距、识别)的训练集拥有不同的最佳声学参数。在1.1节中给出的特征中，有些特征可能是冗余的甚至是不相关的，导致机器学习算法的效率降低、性能损失。

最大相关-最小冗余准则(mRMR)是一种综合考虑特征相关度和冗余度的特征重要性评价准则[16]。定义互信息I(A,B)：

其中，变量A和B的概率密度分别是p(A)和p(B)，其联合概率密度是p(A,B)。设样本数量为m，特征向量数量为n，特征向量fi=[f(i,1),f(i,2),···,f(i,m)]T，I(fi,fj)为样本中第i个和第j个特征的相关性，其中i,j=1,2,3,···,n。设Om为类别标签，I(fi,O)为特征与输出类别O的相关性，其中向量O=[O1,O2,O3,···,Om]T。利用最大相关标准式选择出与类别O相关性大的特征集合D：

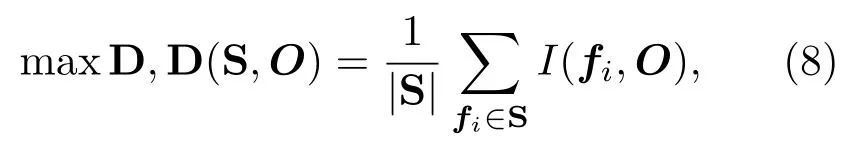
式(8)中，|S|为集合S中所选特征的数量。利用最小冗余标准式剔除特征子集S中的冗余特征的集合R：

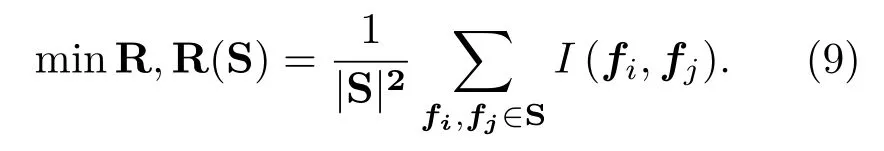
综合以上条件，mRMR方法计算式为

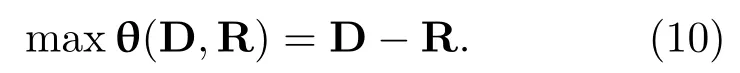
给定具有N−1个特征的集合SN−1，总特征集合为F，计算集合{F−SN−1}中选择第N个特征使得式(10)中的集合θ(D,R)最大：

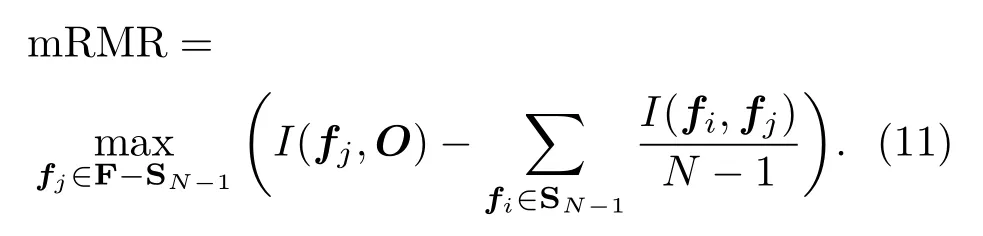
利用mRMR准则对特征空间进行预处理，可以剔除冗余特征，降低计算代价，产生紧凑性和泛化能力更强的模型。算法流程如下：

(1)选择令相关性最大的特征fn，即maxfnI(fn,O)，将所选特性特征添加到空集合S中。

(2)在集合S的补集中找出具有非零相关性和零冗余的特征，如不包含，则转步骤(4)；否则，选出相关性最大的特征fk，即将选中的特征添加到集合S中。

(3)重复步骤(2)，直到S的补集中所有特征的冗余不为零为止。

(4)选择S的补集中互信息熵最大且具有非零相关性和非零冗余的特征fl，即，将选择的特征加入集合S中。

(5)重复步骤(4)，直到S的补集中所有特征的相关性为零。

(6)最后以随机顺序添加与S无关的特征。

1.3 改进的深度神经网络模型

1.3.1 传统前馈深度神经网络

传统的前馈深度神经网络(Feedforward deep neural network,FF-DNN)根据内部的神经网络层可以分为输入层(输入声信号特征的层)、隐含层(所有中间层)和输出层(输出目标距离估计值的层)。单层网络直接相互级联，某一层的任意一个神经元与其上一层的每一个神经元相连。其局部模型可描述为是一个线性运算加上一个非线性转移函数。

设深度神经网络层数为L，l是每一层的索引号，x(l)、y(l)分别是第l层的输入序列和输出序列，网络的输入y(0)=x，w(l)和b(l)为第l层的权重矩阵和偏置向量，f(z)表示非线性转移函数。标准的FF-DNN网络描述如下(对于l∈{0,1,···,L−1层的第i个神经元})[17]：

训练模型时，利用寻优算法对距离估计的代价函数进行迭代优化求极小值，找到合适的线性系数矩阵w和偏置向量b：

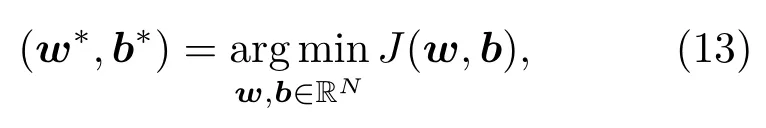
其中，J为代价函数，通常采用输出层输出的目标距离估计值与真实距离之间的均方误差：

其中，N是声信号训练样本数，j是其样本索引号，zj是对应样本的真实距离。关于上述求解优化问题，常使用梯度下降法、共轭梯度法、拟牛顿法等数值优化方法。由于求Hessian矩阵及其逆计算量十分巨大，最常用的优化算法仍然是梯度下降算法。

在声源测距中，传统DNN存在以下缺陷：

(1)测距误差较大。声源距离的代价函数可能高度非凸，迭代过程中容易陷入局部次优解或鞍点。

(2)算法收敛速度慢。梯度下降法的初始学习率和调整策略需人工调节，相同的学习率被应用于各个参数，效率低下。

(3)模型泛化性和鲁棒性弱。全连接网络的模型复杂度过高，参数稀疏度过低，易发生过拟合，以至于对环境变化和信号畸变过于敏感。

要解决以上问题，提高测距性能，重点在于如何改进寻优策略、加快收敛速度、防止过度学习。为此，本文引入1种自适应动态调整学习率的优化方法和2种网络参数稀疏化技术来改进网络模型。

1.3.2 Adam优化算法

由于水下噪声、混响和水声信道的多途干扰，目标距离的代价函数通常为非凸函数且局部次优解，从而需要较大的学习率来跳出局部最优。然而，当在全局最优值附近搜索时，学习率太大会导致过度学习，降低声源测距精度。

Adam算法是一种动态调整参数学习率的自适应优化方法[18]。该方法通过梯度的一阶和二阶矩估计动态调整各网络参数的学习率，在迭代过程中通过偏差纠正使学习率维持在一定范围，从而获得平稳的参数更新，这是解决声源测距问题的理想方法。

设t为迭代次数，w为待估参数，J为代价函数，首先计算梯度的指数移动平均数mt。m0初值为0。综合考虑之前时间步的梯度动量，设系数β1为指数衰减率，有

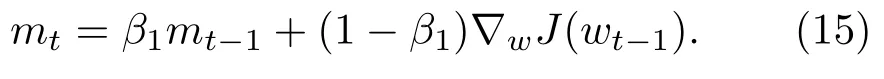
计算梯度平方的指数移动平均数，v0初始化为0。设系数β2为指数衰减率，有

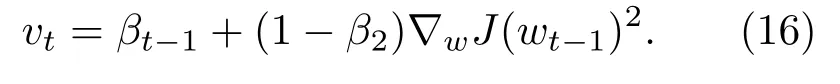
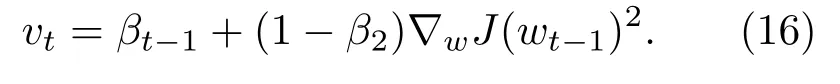
m、v初始化为0会导致mt偏向于0，因此先进行偏差纠正再更新参数：

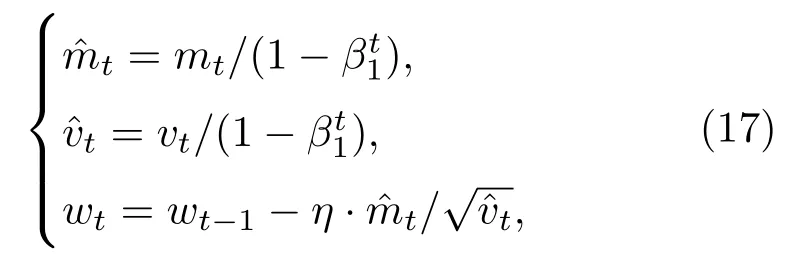
式(17)中，η为初始学习率。算法对更新的步长计算从梯度均值及梯度平方两个角度进行自适应的调节[19]，起到提高迭代效率和测距精度的作用。

1.3.3 网络参数稀疏化

传统的DNN往往受限于特定的水声环境，对环境变化和信号畸变过于敏感，出现过拟合现象。具体表现在迭代过程中训练误差下降到一定程度时，测试误差反而开始增大。为了生成泛用性强的模型，将数据映射到网络特征后，网络特征之间的重叠信息应尽可能少，相关性尽可能低，从而近似于标准正交基。其主要方法是使特征产生稀疏性：稀疏特征有更大可能线性可分，或者对非线性映射机制有更小的依赖[20]。

L2正则化是一种简单且有效的网络参数稀疏化方法。在式(14)加入惩罚项，通过惩罚因子λ控制网络参数稀疏度：

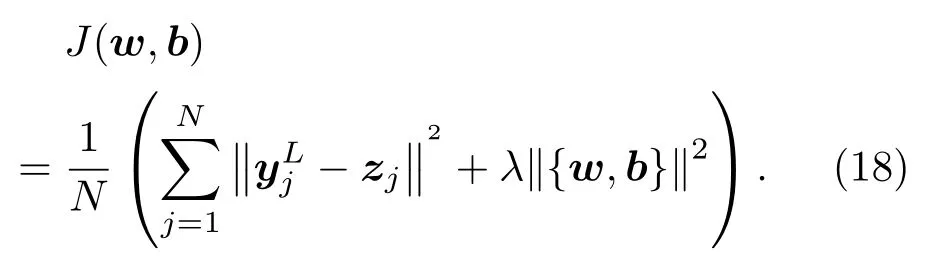
Dropout正则化策略是另一种神经网络稀疏化手段，其核心在于每次权重更新迭代中，对网络的每一层，随机将部分节点对应的权重值置零，使得线性系数矩阵和偏置向量达到稀疏化的效果，在一定程度上避免过拟合的问题。引入Dropout的神经网络描述由式(12)变为[17]：

式(19)中，符号·表示向量点乘，r(l)是一个向量，其元素为服从伯努利随机分布的随机变量，分别以概率P和1−P取1和0为值，参数P是每个神经元的激活概率，通常P取[0.5,1.0]。使用该向量对上一层网络的输出y(l)进行采样，产生一个约减的输出˜y(l)用于下一次网络的输入。这个操作依次进行，从而可以生成一个稀疏的网络结构[17]。这种方法简单易行、节省运算资源，且不会提升优化过程的复杂度。改进后的DNN能够从有效的数据维度上学习到相对稀疏的特征，达到自动提取水声信号关键特征的效果。

2 数值仿真

通过KRAKEN声场计算工具，在声速正梯度浅海环境参数下生成仿真数据。图2描述了本文所使用的环境参数。

图2 环境参数Fig.2 Enviromental parameters

仿真数据包括连续波(Continuous wave,CW)在50 Hz、150 Hz和300 Hz的信号，线性调频(Linear frequency modulation,LFM)信号中心频率为500 Hz、1000 Hz和2000 Hz，频带宽度范围100～1000 Hz，信号长度0.2～1.0 s。将模拟接收信号拷贝100份并分成10组，每一组模拟接收信号分别添加信噪比(Signal-to-noise ratio,SNR)为1 dB、2 dB、3 dB、···、10 dB的高斯噪声。接收点距离分布在1～10 km，深度是分布在5～145 m，网络输入训练集占总样本集80%，由16080个样本组成，剩余20%的数据作为测试集，由4020个样本组成。对生成样本进行多域特征提取，对每一帧得到的特征序列求统计特征，得到均值和方差，对所有帧的自相关系数和频域特征序列求统计特征，得到所有帧的时间均值和时间方差。最终提取到20100个样本的36维特征，作为DNN网络的输入特征，特征空间如图3所示。

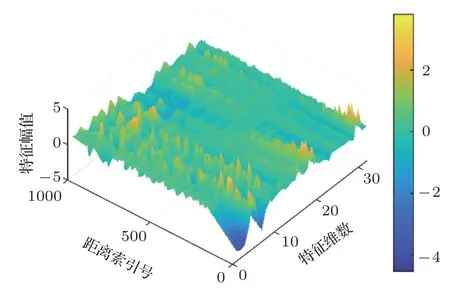
图3 特征空间Fig.3 Feature space

每个特征之间并不完全独立，有些特征与声源距离显著相关，这里根据1.2节中的mRMR算法进行特征选择。基于互信息的mRMR最高效和常用的[21]，在步骤(4)中，输出所选特征的互信息熵作为特征重要性的评价指标，对特征空间上所有特征进行重要度排序，结果如图4所示。

图4中的符号和表1、表2中一一对应，例如DS是下降斜率，SV_Mean是对信号每一帧的谱通量求的平均值；AC_Std是对每一帧自相关系数求的标准差。由排序结果可见与声源距离相关性最强的前3项特征是激励时间、下降斜率和谱通量均值，分别代表激励阶段的时间长度、衰减阶段能量的平均时间斜率和频谱包络面积的均值，这些物理量恰是反映声能量在传播过程中衰减的基本物理量。通常，为了兼顾特征集合的多样性和紧凑性，指标的阈值不宜过大或过小，经测试这里取0.03时，特征子集的维度为29，此时模型收敛性较好。最终得到与声源距离相关性最高的10维时域特征与19维频域特征。

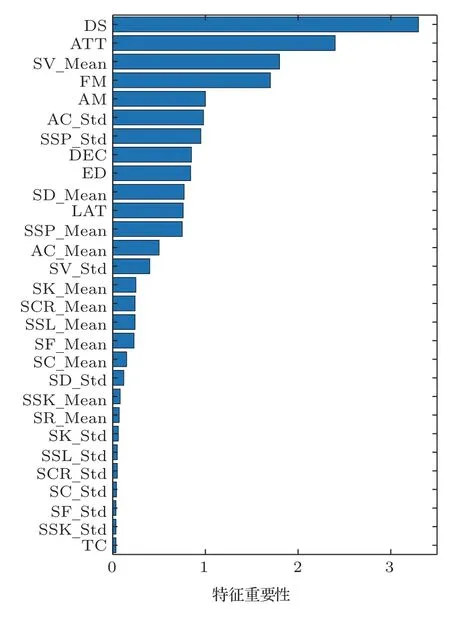
图4 声学参数mRMR重要性排序Fig.4 The mRMR importance ordering of acoustic parameters

神经网络引入Adam优化算法进行网络训练，初始学习率采用0.03，代价函数采用MSE函数，引入Dropout正则化处理，每次迭代神经元激活概率取85%，初始权重由截断高斯分布模型产生，标准差为0.1。经测试双曲正切函数、Sigmoid函数和ReLU函数作为隐含层激活函数均未出现梯度消失现象，其中双曲正切函数在本问题中表现的收敛速度最快，且训练过程中未出现死神经元。隐含层激活函数采用双曲正切函数，输出层采用200个Softmax节点，对应不同的距离的概率，输出值最大的节点对应的距离为距离估计值。网络迭代次数设置为20000次。不同波形参数的单频信号和线性调频信号作为发射信号训练的DNN经20000次迭代后在测试集上的综合测距精确率达到95%以上，最高达到98%以上。以其中一组波形参数(单频信号，f0=150 Hz，zr=35 m，SNR=1～10 dB)的训练和测试结果为例，图5为该组信号的模型训练和测试结果。其中图5(a)给出了训练完成后模型最终在测试集上的距离估计结果，红线代表KRAKEN声场模型中给定的声源距离(即真实距离)，蓝圈代表网络输出的估计距离；图5(b)给出了模型在训练集和测试集上的测量精度随迭代次数的变化曲线。

图5 训练和测试结果Fig.5 The ranging accuracy by iteration times on validation and training sets

以单频信号作为发射信号，改变发射信号频率(f=50 Hz,100 Hz,150 Hz)和声源深度(zS=0～140 m,∆z=20 m)，经10000次迭代，对比不同发射条件下的估计精确率，如图6所示，由图6可见波形参数和声源深度对模型性能的影响小，鲁棒性较好。

图6 不同发射频率下各个深度的测距精确度Fig.6 Ranging accuracy at different depths with different transmission frequencies

以线性调频信号作为发射信号，分析模型的收敛速度和测量精度，经10000次迭代，对不同中心频率(fc=500 Hz,1000 Hz,2000 Hz)、不同频带宽度(fband=100 Hz,300 Hz,500 Hz,700 Hz,900 Hz)和不同时间长度(T=200 ms,400 ms,600 ms,800 ms,1000 ms)的信号源测距结果进行对比。图7～图9给出了不同波形参数的信号的网络训练损失曲线，即训练过程中随着迭代次数增大，测试集上代价函数值的变化曲线。这里的代价函数值为测量的均方误差，下降越快，说明模型收敛速度越快。由此，图7表明模型的收敛速度和测量精度与频带宽度呈负相关，说明频带越宽所含信息越丰富，模型训练需要的时间越长；图8表明模型的收敛速度和测量精度与信号持续时间呈正相关，可见信号持续时间越长，呈现出的特征越明显；图9表明模型的收敛速度与中心频率和测量精度呈负相关，可见浅海中低频的信号特征更加集中，高频信号的特征更加分散，表明模型更适用于远程探测声呐。

图7 信号时长为1.0 s时各频带宽度对应的网络训练损失曲线Fig.7 Network training loss curve with different frequency bandwidth when the signal duration is 1.0 s

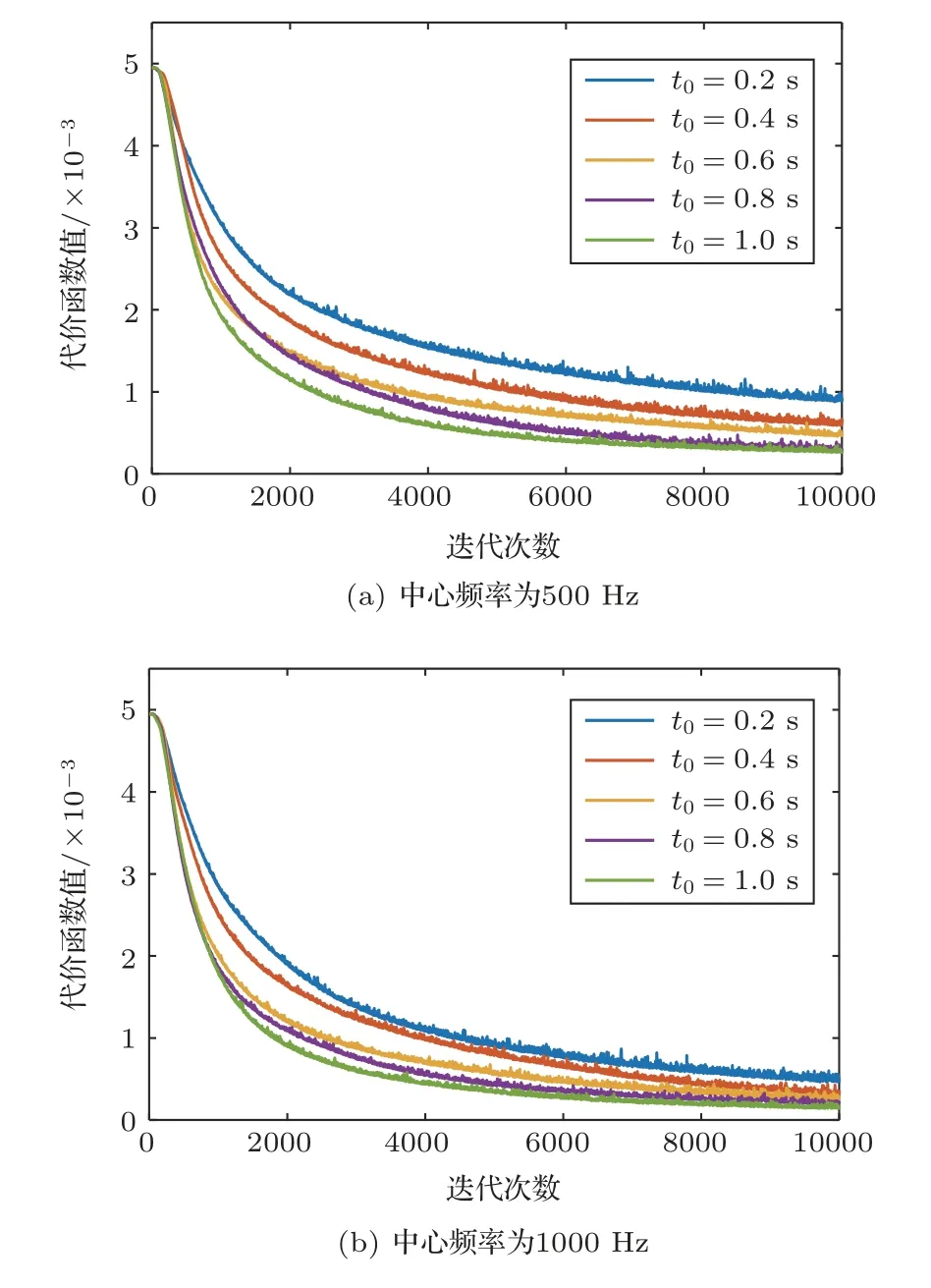
图8 信号频带宽度为500 Hz时不同时间长度对应的网络训练损失曲线Fig.8 Network training loss curves with different time lengths when the frequency bandwidth is 500 Hz

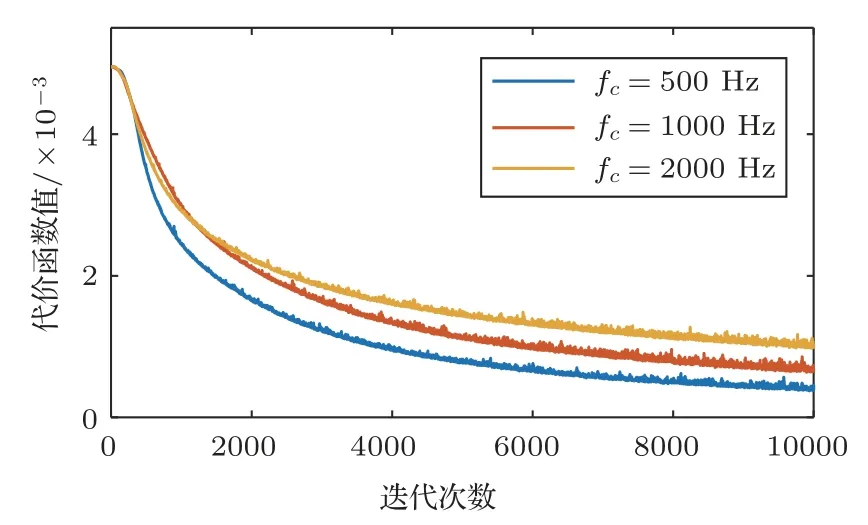
图9 信号频带宽度为500 Hz、时长为1.0 s时不同中心频率对应的网络训练损失曲线Fig.9 Network training loss curves with different center frequencies when the frequency bandwidth is 500 Hz and the duration is 1.0 s

3 讨论和展望

相对已有的深度学习声源测距方法，本文提出的方法可提取信号的多域特征及对特征空间进行筛选，有利于产生紧凑性和泛化能力更强的模型；其次，改进了神经网络模型的寻优算法和参数稀疏化策略，可加快收敛速度并抑制模型过拟合。然而，机器学习是一种监督学习方法，其测距精度以建立功能全、信息丰富的数据库为代价。对于未知的海洋环境、时变的环境参数，需建立大量拷贝数据进行训练并加大网络的复杂度，同时需要已知的声源波形参数，对先验知识和计算资源有较大依赖性。目前已有相关研究[5]通过在真实海洋测试数据的基础上扩充仿真数据，以及采用迁移学习方法来减小深度学习方法对先验知识的依赖性。本文下一步工作将针对海洋测试中远距离测距的实际应用场景，通过建立数据库、优化神经网络结构、提高网络复杂度、增加输出节点数或改进输出层标签形式、增强自学习能力，以提升测距范围和测距分辨率。此外，可通过对数据库进一步扩充与声源目标识别相关的特征和标签，从而在声源被动测距的基础上同时执行目标识别相关的任务，如估计目标材料、形状、运动姿态等，以上需在后续工作中进一步探究。

4 结论

采用一种基于多域特征提取的深度学习方法来实现声源测距，通过浅海环境仿真实例验证了该方法的有效性，并分析了波形参数对测距性能和模型收敛速度的影响。本方法构建了声信号在时、频域的多维感知特征量，采用最大相关-最小冗余准则(mRMR)提取了声源和水下声场的关键信息，在传统深度神经网络的基础上引入自适应矩估计(Adam)优化、L2正则化和Dropout正则化处理，提升模型的收敛速度和泛用性。结果表明：此方法在模型训练过程中收敛速度较快，预测性能较稳定，在所定条件下测试集上声源的综合测距精确率可达到95%以上，能够实现对声源距离的有效估计。此外，对不同发射信号训练效率的对比表明，算法性能对波形参数和声源深度具有良好的鲁棒性，模型收敛速度和测距精度对于带宽较小、持续时间长的瞬态发射信号较高。训练后的模型在单次测距任务中仅需执行毫秒级运算，可实现数据的实时处理。

本文提出采用的声源测距的深度学习方法，紧密结合了和海洋环境、传输距离相关的声源信号时频域多维感知特征，测试集上声源测距精度优良、可信。未来，建立并不断更新充实功能齐全、信息丰富的各种典型海洋环境参数、传输距离及声源信号多域特征大数据库，进一步优化算法和自学习能力后，本方法可望实现实时准确的水下目标被动定位、跟踪和分类识别，是今后深入研究的目标和方向。