基于混合有限元-统计能量分析的箱梁结构噪声特性分析∗

余亮亮 雷晓燕 罗锟

(华东交通大学 铁路环境振动噪声教育部工程中心 南昌 330013)

0 引言

近年来，我国城市轨道交通发展迅猛。然而在城市轨道交通体系中，高架轨道占比只有百分之十几。制约着高架轨道结构在城市交通体系运输中应用的主要原因是高架轨道结构振动和辐射噪声。针对以上问题，国内外对桥梁结构振动噪声都进行了一系列研究，目前主要的方法有理论分析、现场测试等。

理论分析方面，李小珍等[1]采用车-轨-桥耦合理论，讨论了桥梁的竖向振动规律，以及梁体面板的声学贡献率和贡献量。张迅等[2]利用混合有限元-统计能量分析(Finite element-statistical energy analysis,FE-SEA)模型对混凝土箱梁低频结构噪声进行预测并验证。高飞等[3]对桥梁与车辆参数进行了研究，分析了其对高架结构振动噪声的影响规律。罗文俊等[4]基于混合FE-SEA方法对箱梁结构噪声进行预测分析，但仅仅建立了箱梁结构，没有考虑钢轨以及轨道板等结构。李奇等[5]采用有限元法以及模态叠加法对列车-轨道-桥梁动力相互作用的系统瞬态响应进行求解计算，重点分析桥梁高频局部振动。宋雷鸣等[6]根据动力学基本理论，通过建立车-桥耦合模型，将轮轨力作为统计能量分析的荷载输入，研究了高架结构的振动噪声，并进行了相应的实验验证。韩江龙等[7]采用模态叠加法对轨道交通槽型梁进行车-轨-桥耦合动力求解计算，结合SYSNOISE软件解得模态声传递向量，进而计算桥梁的结构噪声。Thompson及其团队[8−11]对铁路环境噪声振动与控制做了大量研究，并开发出相应软件，用于指导铁路相关设计。然而，采用数值分析方法往往对实际情况进行了一定程度的简化，得出的结论具有一定的局限性。

现场实测方面，在早期，Stüber[12]实测了两座钢桥在电气机车以80 km/h的速度经过时的桥梁噪声，表明自重与桥面板阻尼的增加有利于减小结构噪声。Ngai等[13−14]对香港一座混凝土箱形梁的测试表明列车以140 km/h的速度经过时，产生的噪声与振动在20～157 Hz范围内，并且在43 Hz和54 Hz处有峰值。近期，常亮[15]对武汉某25 m箱形梁进行了噪声与振动现场测试，测试发现车辆以50 km/h的速度通过时箱形梁最大振动出现在底板与翼缘板，并且振动频率在40～90 Hz范围内。Li等[16]和Zhang等[17]对高速铁路32 m双线与单线混凝土箱形梁的振动与噪声进行了现场实验研究，实验结果表明，箱形梁振动产生的结构辐射噪声主要是低频率段的噪声，并且在50 Hz与63 Hz存在峰值；箱形梁的结构噪声主要由箱形梁板件局部刚度决定。采用现场实验测试方法研究桥梁结构噪声虽然能获得多因素作用的综合结果，但难以形成系统的规律，同时会影响交通，耗费大量人力、物力资源，并且很难满足规划、设计阶段的具体要求。

模型试验分析主要是通过相似理论建立特定比例的缩尺模型，使原型与模型之间满足一定的相似关系。目前利用模型试验来研究桥梁结构噪声的文献极少，作者及其团队以某高铁32 m箱梁为原型，制作了10:1的缩尺模型，通过模型试验的方法对箱梁结构振动噪声进行了一系列的研究，并取得一系列成果[18−20]。

混合FE-SEA方法能够避免多个模型的分频求解，在保证计算精度的同时能够提高效率，并且保证模型的一致性。但是，基于模型试验的混合FE-SEA方法目前尚未相关学者进行研究。本文将混合FE-SEA方法应用在高架轨道箱梁1/10模型中，旨在为铁路桥梁噪声提供一种准确快速的分析方法。首先，利用商用软件VAONE建立箱梁FE-SEA模型，其中箱梁采用FE模型，轨道结构采用SEA模型，将激振器的荷载激励作为能量输入，并进行频域计算。然后将仿真结果与实验室测试数据进行对比，验证了模型的准确性。在此基础上，对箱梁结构子系统的声贡献量及其振动传递规律进行分析。

1 混合FE-SEA基本理论

Shorter等[21]对混合FE-SEA理论做出了重要的贡献。一般而言，确定性子系统的总体动力方程可以表示为

其中：N为SEA子系统的个数；u为FE子系统全部的自由度；f(k)re表示第k个SEA子系统在边界上对FE子系统产生的混响场荷载(Reverberant force)；fex为作用在FE子系统外部激励；Dto为FE子系统的总体动刚度，可表示为

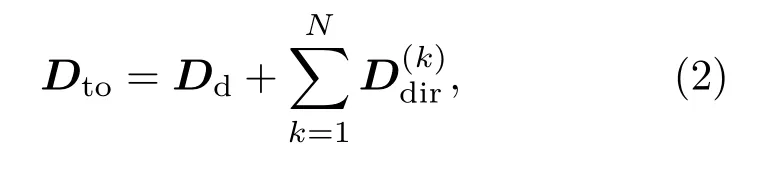
其中：Dd表示边界处FE子系统的自身的动刚度，通常可通过FE分析模型得出；表示第k个SEA子系统对FE子系统的直接动刚度。

由式(1)可知，FE子系统的自由度u可以表示为

当SEA子系统中有足够的参数为不确定性时，耦合边界上的混响力可由扩散场的互易关系表示：

通过式(3)～(4)，可得FE子系统自由度u的互谱矩阵：

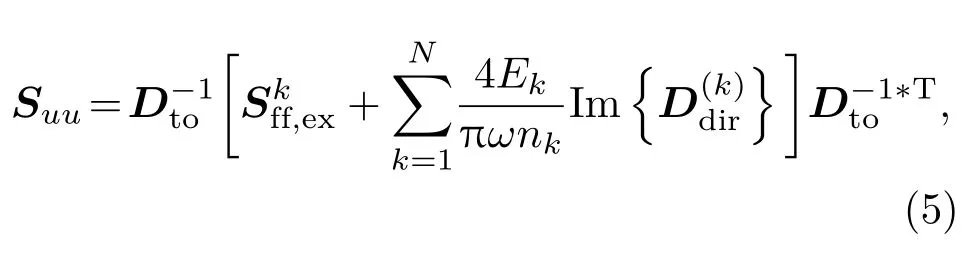
其中，Sff,ex表示作用在FE子系统上的外荷载互谱矩阵；“*”表示共轭运算，“T”表示转置运算。

同时，混合FE-SEA系统的功率平衡方程可表示为

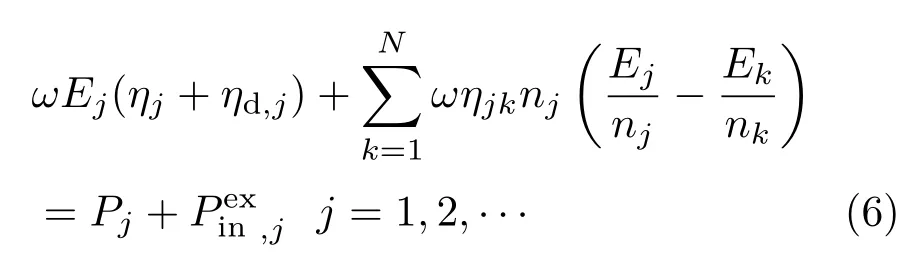
式(6)中：

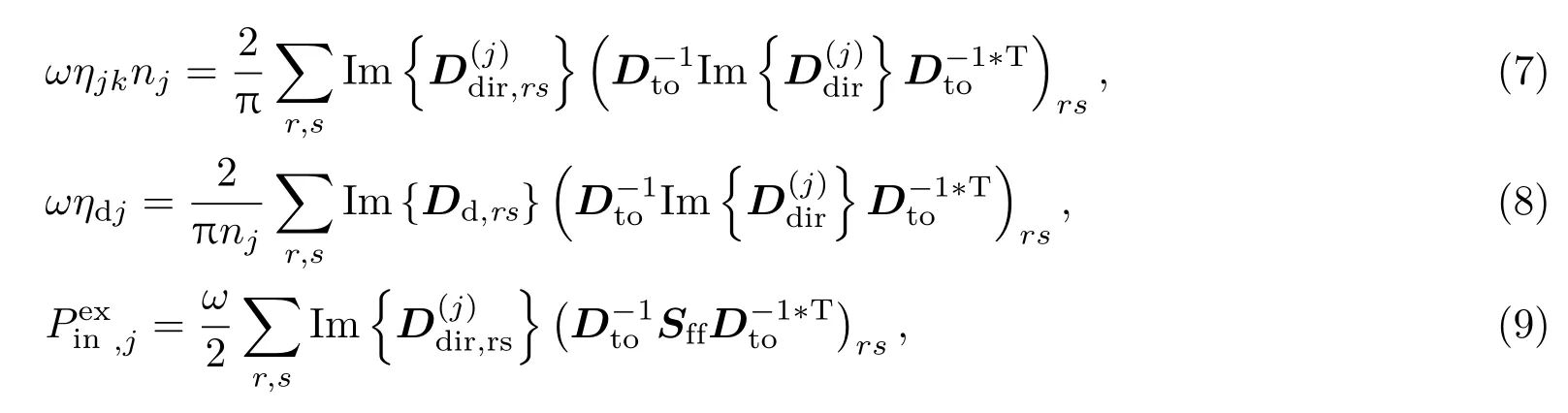
其中，ηjk是在SEA子系统中j和k之间的功率流耦合损耗因子；ηj为结构中SEA子系统与FE子系统j的阻尼损耗因子；Pj为在SEA子系统j上的外界输入功率；是外部激励施加在FE子系统上对第j个SEA子系统产生的输入功率；Sff为施加到FE子系统的力的互谱矩阵。

由公式(6)可以得到各SEA子系统的平均振动能量，再由公式(5)，根据SEA子系统作用在FE子系统上的荷载与SEA子系统的能量响应之间的关系，可得FE子系统的自由度，进一步，可以得到FE子系统的振动速度、加速度等。最后，通过声辐射理论可以求出空气中的任一点的声压。

2 数值仿真分析

2.1 仿真分析流程

首先将实验测试时利用激振器施加的荷载从LMS Test.Lab中导出，通过快速傅里叶变换(Fast Fourier transformation,FFT)把力信号从时域转换到频域，同时，基于波动耦合分析理论，建立混合FE-SEA模型，然后将频域的力导入到VAONE中，以激振器的荷载作为外界能量的输入，加载在箱梁跨中断面的钢轨子系统上。求解得到桥梁结构的振动响应，然后根据声辐射理论求得桥梁轨道结构噪声。具体仿真流程如图1所示。

图1 箱梁轨道结构仿真分析流程图Fig.1 Flow chart of simulation analysis of box beam track structure

2.2 混合FE-SEA模型的创建

VAONE软件作为当前主流的能够用于中高频分析的软件，在国际学术界和工程界得到了广泛应用。如图2所示，利用商用软件VAONE创建基于波动耦合理论的混合FE-SEA计算模型，根据轨道结构的不同性质，主要将其分为3类子系统，其中箱梁结构子系统采用FE子系统，为箱梁系统中的确定性结构。箱梁结构系统中各板(底板、翼板、腹板、顶板)采用板单元(FE-plates)模型；无咋轨道结构子系统采用SEA子系统，利用板单元(SEA-plates)建模；钢轨子系统采用SEA子系统，使用梁(SEAbeams)单元模型；无砟轨道结构子系统和钢轨子系统之间采用手动SEA点连(Manual SEA point Junction)，模拟扣件的连接。箱梁子系统结构在支座位置采用简支约束。无砟轨道结构与箱梁之间采用手动混合连接(Manual Hybrid Junction)。具体流程如图3所示。

图2 箱梁结构混合FE-SEA计算模型Fig.2 Mixed FE-SEA calculation model of box girder structure

图3 混合FE-SEA建模流程图Fig.3 Flow chart of model building with mixed FE-SEA

图4为各子系统间的功率流传递示意图，钢轨结构子系统在外荷载的激励下，产生竖向弯曲振动，当钢轨的振动能量通过无砟轨道结构传给箱梁结构时，根据振动能量传递关系，可以将箱型梁结构子系统划分为左右翼板子系统、左右腹板子系统、顶板子系统以及底板子系统。图4中的方框表示各子系统，子系统之间的连线表示子系统之间的功率传递路径。各子系统的特征如表1所示。其中，序号7为外部虚拟声场，通过连接半无限流体(Semi-infinite fluids)能够预测箱梁轨道结构声辐射。

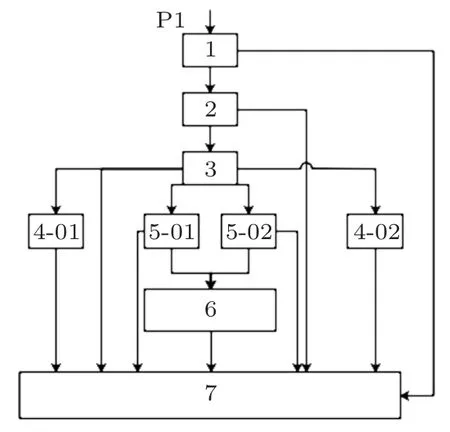
图4 子系统之间的功率流传递示意图Fig.4 Schematic diagram of power f low transfer between subsystems

表1 箱梁结构子系统的分类Table 1 Classification of box beam structural subsystems

2.3 参数选择

采用FE模型对箱梁振动响应及其声辐射问题进行分析时，各单元尺寸不应超过振动波长的1/6。本文对箱梁振动噪声的分析频率为20～800 Hz，单元边长取0.02 m，总共划分为4834个单元。在箱梁的浇筑过程中，制作了相应的试块，并对基本参数(弹性模量、密度等)进行了测试。损耗因子取0.01，为普通混凝土试块的平均值。箱梁的具体参数见表2。

表2 箱梁结构参数Table 2 Structural parameters of box girder

钢轨为由厂家定制的CHN60型钢轨1/10的缩尺模型，其中，钢轨密度为6870 kg/m3，弹性模量为174 GPa，泊松比为0.3。

桥上无砟轨道由3部分组成：轨道板，其长度为645 mm，宽度为255 mm，厚度为30 mm；自密实混凝土模拟层，其长度为3200 mm，宽度为260 mm，厚度为10 mm；底座板，其宽度为295 mm，厚度为19 mm。

利用LMS施加的荷载信号有正弦信号、随机信号等，本文采用猝发随机信号源，能够更好地体现荷载的随机性。激振器所施加的激励如图5所示。

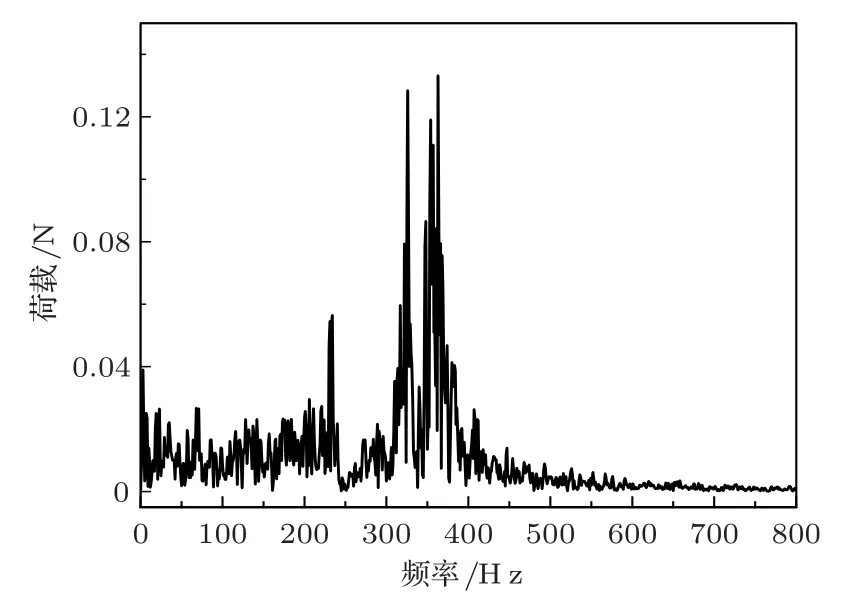
图5 激振器荷载频谱图Fig.5 Vibrator load spectrum

3 预测模型的实验验证

在混合模型的求解过程中，首先对FE系统进行求解，将求解的模态结果作为中间求解，最后求解声辐射响应。因此，进行验证时，首先通过模态测试进行箱梁模态验证，然后对比各场点的声压级，最后将本模型的计算效率与其他文献进行比较。

3.1 实验方案

3.1.1 模态测试

(1)自由模态测试

测试中采用的主要设备有比利时LMS公司310数据采集系统，振动传感器采用PCB356A16型三向加速度传感器，力传感器型号为PCB208C02。

采用LMStest测试软件对模型进行激励，采用随机猝发信号进行测试，信号通过功率放大器，然后通过激振器将力激励作用在模型上，再通过传感器采集结构振动信号，最后通过LMS系统的模态识别模块，对箱梁结构的模态进行识别。

为了准确测得箱梁的自由模态，通过预实验分析确定了一组布置方案：总共布置9个断面，每个断面分别布置8个点，整体箱梁结构共计布置72个拾振点。其拾振点与激振点布置如图6所示。实验时采用自由悬置方式进行垂向激振，实验测试如图7所示。

图6 箱梁模态测点布置示意图Fig.6 Schematic diagram of box beam modal measurement points

图7 箱梁自由悬挂状态Fig.7 The free suspension of the box girder

(2)约束模态测试

约束模态的测试方法与自由模态测试结果大致相同，仅仅是对箱梁结构进行了支座处的焊接处理，用来模拟对箱梁的约束，此处不再赘述。

3.1.2 声学测试

将缩尺箱梁置于半消声室内，在箱梁跨中断面布置声学传感器进行声压级实测，以验证箱梁结构噪声计算模型的准确性。采用的主要仪器设备有：激振器、24通道HEAD噪声采集分析系统以及GRAS声学传感器等。如图8所示，在箱梁结构跨中断面布置3个GRAS声学传感器，包括：底板下方0.3 m的N1处1个，顶板上方0.3 m的N2处1个，翼板下方0.3 m的N3处1个。测试前，做一定的隔声处理，尽可能提高测试结果准确性。测试分5组进行，每组测试时间30 s，实测如图9所示。

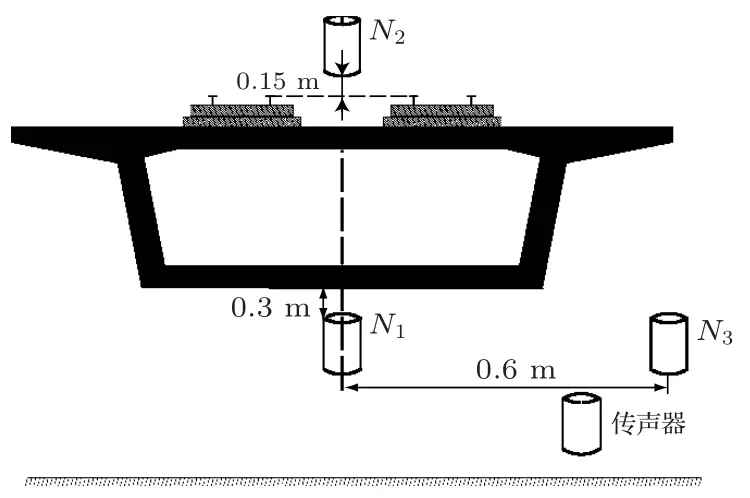
图8 箱梁模型跨中截面测点布置图Fig.8 Layout of measuring points for mid-span section of box girder model

图9 实验室测试照片Fig.9 Laboratory test photo

3.2 结果比较分析

3.2.1 模态分析

图10和图11为箱梁在自由状态和约束状态下的振型图，从图中可以看出在自由状态和约束状态，所建立的模型振型与实测振型基本保持一致。表3为箱梁在前5阶模态的实测与仿真结果，仿真和实测的误差几乎都在合适范围内，第3阶模态尽管误差较大，但实测与仿真的振型仍保持一致。

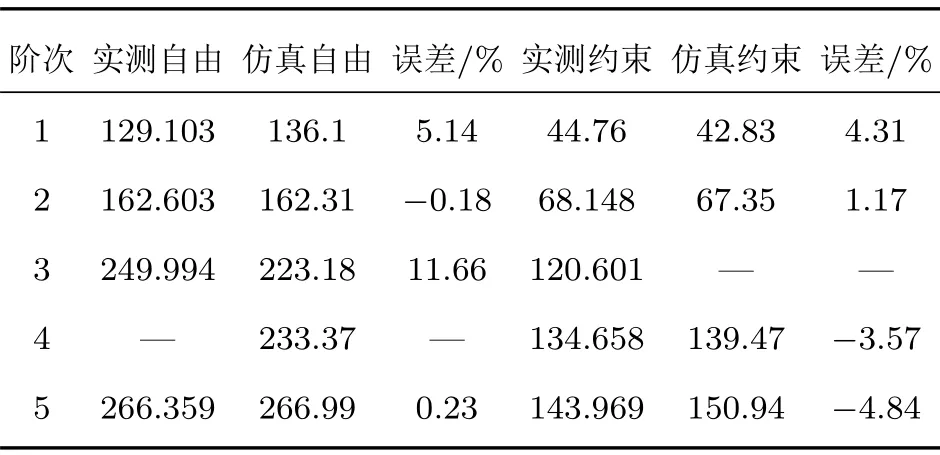
表3 实测与仿真模态对比Table 3 Comparison of measured and simulated modes

图10 约束状态下实测与仿真的1、2、4、5阶模态Fig.10 Measured and simulated 1,2,4,and 5 order modes under the constrained state

图11 自由状态下实测与仿真1、2、5阶模态Fig.11 Measured and simulated 1,2,and 5 order modes in free state

3.2.2 近场声压级对比分析

计算了混合FE-SEA模型的模态之后，计算与实测位置相同的N1、N2、N3点的声压级，并与实测进行比较。图12～14为场点N1、N2、N3的声压级对比图，从图中可以看出各场点的声压级最大值均出现在315～400 Hz附近，这是因为施加的外荷载的激振频率的峰值就在315～400 Hz附近。各点的实测噪声值与仿真结果吻合得较好，都在400 Hz处达到峰值。同时，各场点的实测与仿真的声压级趋势吻合较好，说明本模型是能够准确预测箱梁轨道结构的噪声。

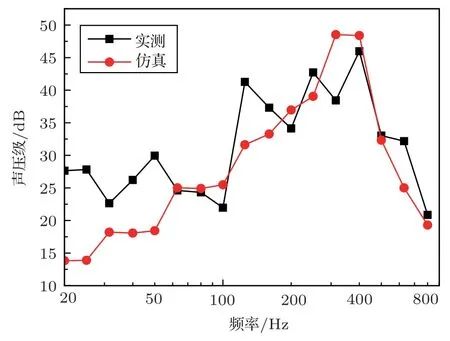
图12 N1点声压级实测与仿真对比Fig.12 Measured and simulated comparison of N1 point sound pressure level

图13 N2点声压级实测与仿真对比Fig.13 Measured and simulated comparison of N2 point sound pressure level

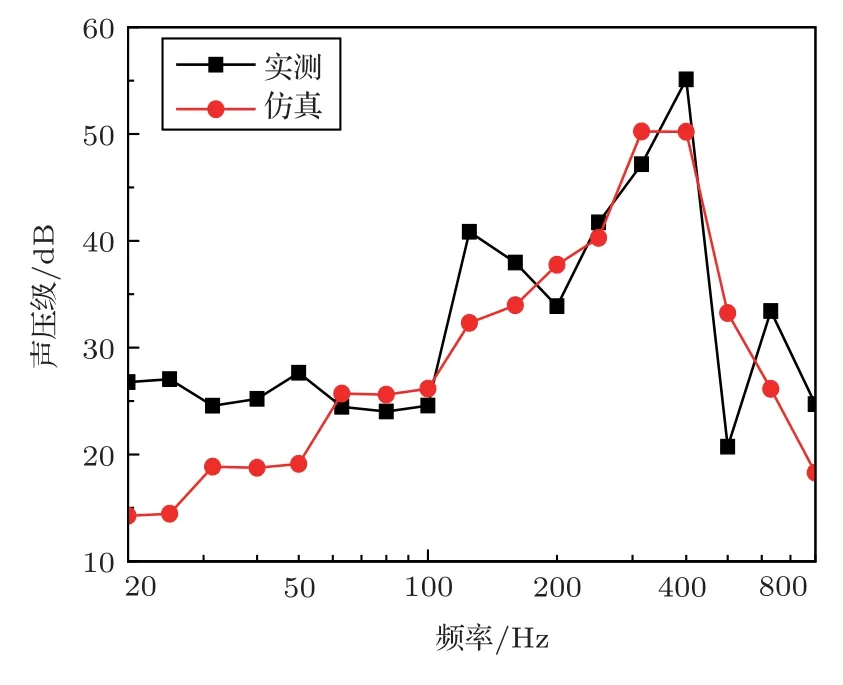
图14 N3点声压级实测与仿真对比Fig.14 Measured and simulated comparison of N3 point sound pressure level

3.2.3 计算效率对比分析

本文采用的是10:1箱梁缩尺模型，单元数是4834，采用混合FE-SEA方法具有较高的计算效率，能够大大缩减计算时间。本模型在采用四核3.0 GHz CPU和12 GB内存容量的情况下，计算时间不到10 min，与其他计算方法(见文献[15])比较效率较高，对于快速预测高架轨道结构噪声具有很大的优势。表4是不同方法的计算效率比较。

表4 不同模型计算效率对比Table 4 Comparison of calculation effi-ciency of different models

4 箱梁声辐射计算和声贡献量分析以及振动传递规律分析

4.1 远场声辐射分析

为了研究远场位置箱梁的声辐射特性，如图15所示，在箱梁的跨中断面布置点P1、P2、P3，其中P1和P2分别距离轨面以上0.35 m和0.12 m；P3距离箱梁底部0.3 m。各点距离轨道中心线的水平距离为2.5 m。由图16可知，点P1、P2、P3虽然距离箱梁的位置各不相同，但是在远场的声压级基本保持一致，说明在远场箱梁结构可以视为点声源。

图15 远场测点位置示意图Fig.15 Schematic diagram of the location of the far-field measuring point

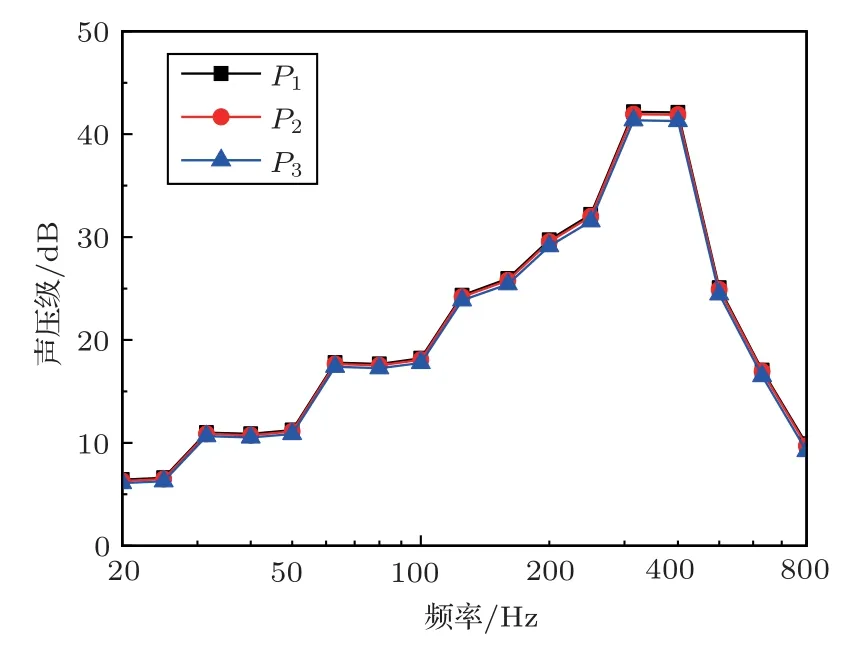
图16 远场位置声压级Fig.16 Far-field position sound pressure level

4.2 声贡献量分析

为了研究远场位置箱梁各部分的声贡献量，箱梁结构可看成由顶板、底板、近轨腹板、远轨腹板、近轨翼板、远轨翼板6个子系统组合而成，图17给出了6块板对场点P1的贡献量。从图中可知各场点的总声压级的峰值频率在315～400 Hz范围内，声压级的峰值为42.17 dB。场点P1处的辐射声压级的峰值频率范围在315～400 Hz。同时，在峰值频率处，声贡献量的大小关系为近轨翼板>顶板>远轨腹板。主要是因为在竖向荷载作用下，翼板和顶板的振动响应剧烈，腹板的振动响应较小。

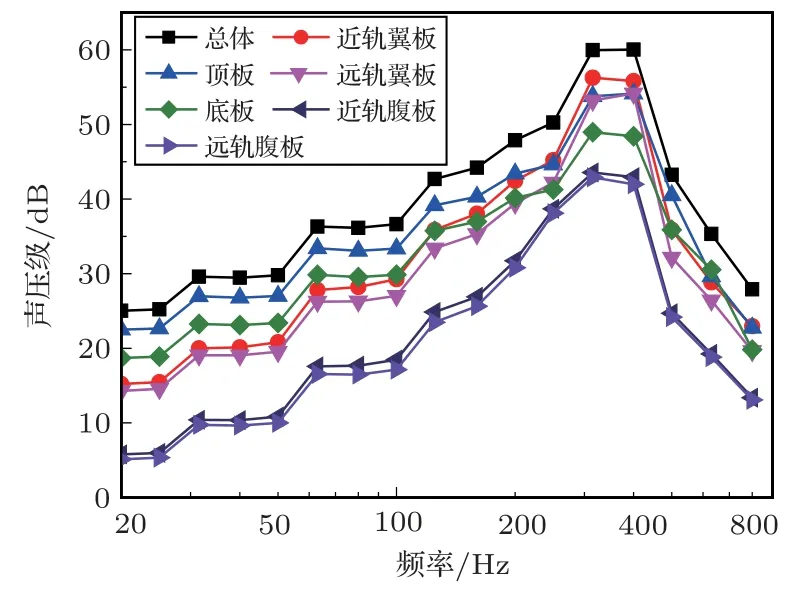
图17 场点P1处箱梁各板声贡献量级Fig.17 Sound contribution level of each plate of box girder at point P1

表5和图18为各场点的声贡献量分析汇总，从图18中可以明显看出顶板和左右翼板的声贡献量高达87.3%，底板贡献量只有8.4%，而左右腹板的声贡献量仅为4.3%。因此顶板和翼板应该为噪声控制的主要对象。

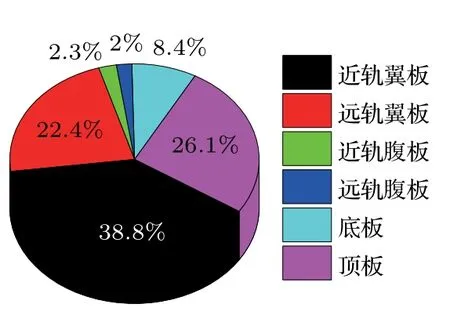
图18 场点P1各板的贡献量Fig.18 The contribution of each board at point P1

对比文献[4]可知，尽管荷载激励形式不一致，但是，在竖向荷载作用下，箱梁结构各子系统的声贡献量的大小规律是一致的，同时箱梁结构噪声的峰值频率也与荷载的激励峰值频率保持一致。

表5 远场声压级各板的声压级贡献量Table 5 Sound pressure level contribution of each plate of far-field sound p ressure level(单位：d B)

4.3 振动及其传递规律

图19为箱梁各子系统的振动加速度级，由图19可知：各板均在315～400 Hz处达到振动峰值，近轨翼板的振动加速度响应最大，远轨腹板的振动加速度响应最小，这与各板声贡献量的规律一致，说明箱梁结构声辐射与板件振动密切相关。

图19 箱梁跨中断面各板块中点的振动加速度级Fig.19 Vibration acceleration level of midpoint of each plate of cross section of box girder

图20为结构的振动功率传递规律，由图20可知：在20～400 Hz的范围内，从钢轨到轨道板结构的传递损失比轨道板结构传递到箱梁结构的损失要小，但在400 Hz以上部分损失规律正好相反；振动传递规律的功率的峰值频率同样也在400 Hz，与箱梁振动噪声的峰值频率保持一致。

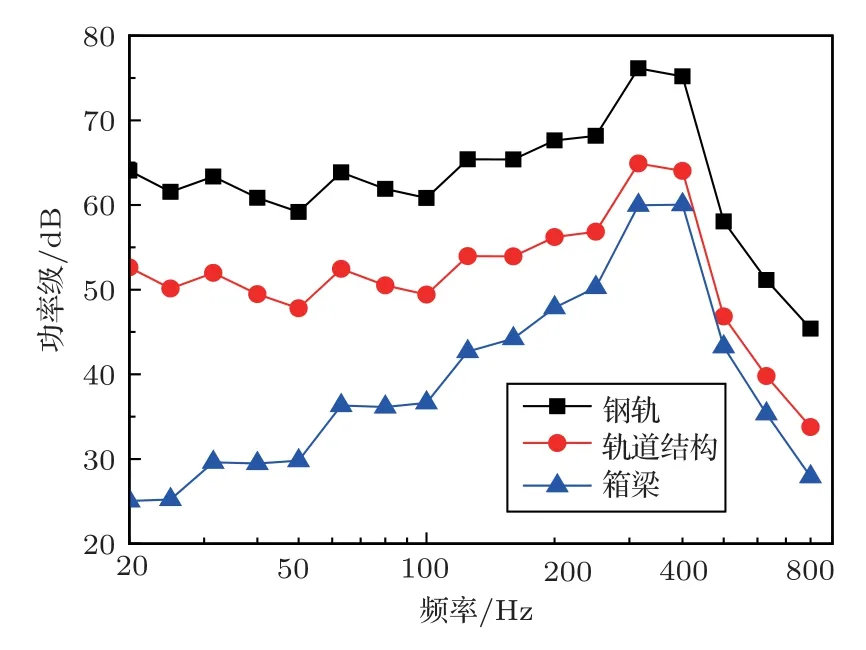
图20 箱梁结构振动功率传递Fig.20 Box beam structure vibration power transmission

图21给出了振动能量，由图21可知：各板的振动能量的峰值频率为400 Hz，在20～200 Hz的范围内顶板的振动能量最大，但在400 Hz的峰值频率处，近轨翼板>远轨翼板>顶板>底板>近轨腹板>远轨腹板。因此在进行减振处理过程中，应该重点关注顶板和翼板的振动。

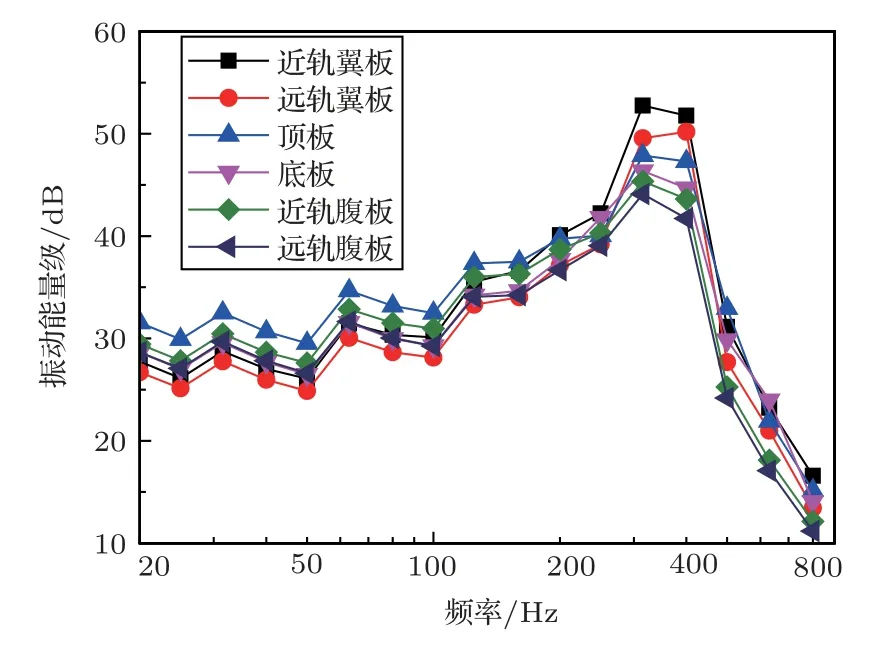
图21 箱梁各子系统振动能量级Fig.21 Vibration energy level of each subsystem of box girder

5 结论

本文采用FE-SEA混合法建立了高架轨道结构箱梁1/10模型，并利用半消声室进行声学实验以及模态测试，并得出主要结论如下：

(1)混合FE-SEA模型得到的箱梁结构辐射的声压级与实验室实测结果吻合良好，说明此方法精度很高。

(2)在随机荷载的激励下，箱梁顶板和左右翼板的声贡献量高达87.3%，而底板和左右腹板的声贡献量仅为12.7%，且与箱梁子系统的振动大小规律一致，因此在减振降噪过程中着重注意顶板和翼板。

(3)外荷载的激励频率的峰值与振动噪声的峰值保持一致，因此在箱梁结构减振降噪过程中，可以从外荷载方面考虑。

(4)利用模型试验的对比分析，能够很好地反应桥梁结构轨道结构噪声的声辐射规律以及声贡献量的大小规律，且与原型桥规律一致，为快速预测高架轨道箱梁结构噪声提供了重要方法。