非高斯环境下的深度学习脉冲信号去噪与重构∗

李悦 马晓川 王磊 刘宇

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院水下航行器信息技术重点实验室 北京 100190)

(3 中国科学院大学 北京 100049)

0 引言

近年来，为顺应现代海战的演进趋势，水下对抗正朝着体系化、无人化、智能化方向发展。在有关海区及时侦测未知声呐发射的脉冲信号，并分析其性能是水声对抗的重要任务之一。由于声源位置的远近未知，加上海洋环境变化多端，致使接收信噪比较低，因此需要利用适当的去噪方法对脉冲信号进行增强，以便进行后续的信号处理与分析。

脉冲信号持续时间较短，传统的自适应滤波去噪方法难以在脉冲持续时间内有效收敛，并且传统方法中大多基于环境噪声为高斯分布的假设，经过研究，实际应用中的海洋环境噪声还常常表现为非高斯分布。α稳定分布的脉冲噪声以及非平稳的行船噪声是海洋环境中两种常见的非高斯噪声。当假设背景噪声为高斯噪声时，可利用水声信号的二阶或高阶统计量进行信号处理，由于分数低阶的α稳定分布不存在有限的二阶及以上各阶统计量[1]，此类算法在这种情况下会发生性能下降，另外非平稳行船噪声也会为传统的基于自适应滤波的去噪方法收敛带来困难。

短时傅里叶变换(Short time Fourier transformation,STFT)是一种线性时频分析方法，其算法实现简单高效，并且不会产生交叉项，在工程实践中得到了广泛的应用。随着深度学习领域的蓬勃发展，近年来出现了大量利用深度学习方法进行语音增强的研究，这些研究利用语音信号STFT幅值特征进行语音信号去噪与重构。文献[2–3]利用卷积神经网络(Convolutional neural network,CNN)学习带噪信号STFT幅值与纯净信号STFT幅值之间的映射关系实现去噪，文献[4–5]利用循环神经网络(Recurrent neural network,RNN)建立各帧数据上下文之间的关系，利用前后序列的相关性进行去噪，也取得了较好的结果。相较于RNN，CNN网络参数更少，并且不存在RNN网络的长期依赖问题，更易于训练。CNN语音增强模型利用增强语音幅值特征与原带噪语音谱的相位分量来重构信号。语音信号的去噪仅对幅值谱进行处理，是因为相位对于语音信号的可懂度影响不大[2]，然而对于水声脉冲信号其相位与幅值特征均是重要的信息。文献[6]提出一种DnCNN的图像去噪网络，可在未知背景噪声级的情况下实现盲去噪，利用残差学习(Residual learning,RL)和批标准化(Batch normalization,BN)提升模型性能。经研究，深度神经网络模型相较于恒等映射更易于学习残差映射，因此本文借鉴DnCNN，利用残差学习的思想，学习带噪信号STFT特征和带噪信号与纯净信号STFT特征值残差之间的映射关系，与之前提到的CNN语音增强网络不同的是，本文脉冲信号去噪网络的输入包含STFT特征的实部和虚部两个通道，并不仅是幅值特征，学习的目标是残差的实虚部两通道分量。文献[7]指出批标准化仅在高斯分布噪声条件下具备良好的性能，本文训练集噪声包括高斯及另外两种非高斯噪声，为提升模型在复杂噪声场景中的泛化性，模型去掉批标准化层。本文模型相较于传统去噪方法主要有以下优点：首先，深度学习可以通过训练使模型适用于多种类型脉冲信号及环境噪声，再者，传统方法如自适应滤波方法对参数设置如权值初值、更新步长等较为敏感，而训练完毕的神经网络仅根据输入带噪数据进行计算，无需人为设定参数。

本文针对两种常见的非高斯环境中脉冲信号的去噪问题，提出一种基于深度学习的处理手段。首先对接收带噪信号进行STFT，提取其实部与虚部分量，之后建立全卷积的水声脉冲信号去噪网络，实现多种环境噪声中的多种脉冲信号的增强，最后通过逆变换重构脉冲信号的时域序列。本文仿真3种常见脉冲信号：连续波(Continuous wave,CW)信号、线性调频(Linear frequency modulation,LFM)信号、双曲调频(Hyperbolic frequency modulation,HFM)信号，添加高斯噪声、α稳定分布噪声以及非平稳行船噪声，生成不同信噪比或广义信噪比下的样本，用以训练模型。通过在仿真测试集以及实测样本上的测试，并对比传统去噪方法，验证本文方法在脉冲信号去噪与重构任务中的有效性。

1 非高斯噪声

常见的声呐发射脉冲信号有CW信号、LFM信号、HFM信号等。实际水声环境中的噪声常呈现非高斯分布。由于工业活动、地震风暴及海洋生物等因素的影响，会存在大量的脉冲干扰，这种噪声可用α稳定分布来描述[8]。另外行驶船舶也会产生一种非平稳噪声，本文主要研究高斯噪声和这两种非高斯环境噪声中的脉冲信号增强。

1.1 α稳定分布噪声

α稳定分布又称非高斯分布、重尾分布。α稳定分布的概率密度函数除少数特例外并不存在统一、封闭的解析表达式，一般使用特征函数来描述其分布特性[9]。

若随机变量X服从α稳定分布，当且仅当其特征函数满足

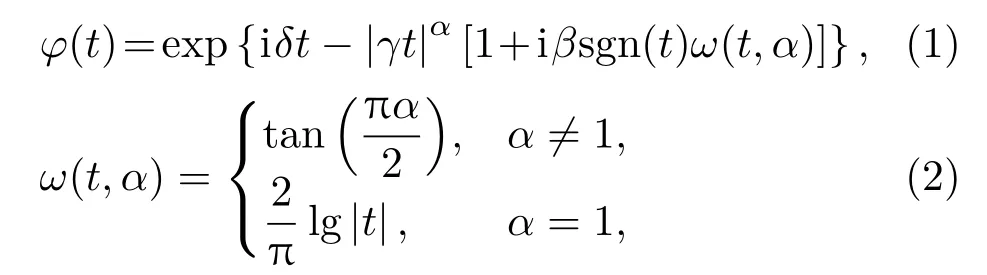
其中，0<α≤2，−1≤β≤1，γ>0，−∞<δ<∞。

α稳定分布用4个基本参数来描述其主要特征。特性指数α决定概率密度函数的拖尾厚度，α越小拖尾越厚重，冲击性越强。偏斜参数β是分布对称程度的度量，当β=0时，分布对称；β<0时，分布具有右偏态；β>0则表示分布具有左偏态。尺度参数γ表示分布偏离均值的离散程度，类似于高斯分布中的方差。位置参数δ类似于高斯分布中的均值，表示了分布的位置[10]。

由于α稳定分布噪声不存在有限的二阶统计矩，无法表示其方差，因此将传统意义上的信噪比进行重定义，称为广义信噪比(Generalized signal-tonoise ratio GSNR)[11]，如式(3)所示：

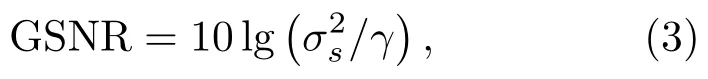
1.2 非平稳行船噪声

行驶船舶的辐射噪声是一个非平稳的随机过程，可以用局部平稳过程来拟合[12]，文献[13]利用如下的信号模型仿真行船噪声：

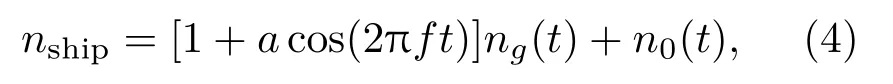
其中，ng(t)表示高斯白噪声，n0(t)表示环境噪声，为体现舰船噪声的非平稳性，调制幅度a可随机变化。

2 脉冲信号去噪卷积神经网络模型

针对多种复杂背景噪声中的3种脉冲信号(CW，LFM，HFM)的去噪及重构问题，本文提出一种基于深度学习的方法，系统流程图如图1所示。首先对传感器接收信号x(t)进行STFT，获得STFT复数谱X(m,k)并输入去噪卷积神经网络中，输出去噪信号复数谱S(m,k)，最后通过逆变换可获得去噪信号的时域序列(t)。

图1 系统流程图Fig.1 System f low chart

2.1 特征提取

传感器接收信号x(t)为纯净脉冲信号s(t)与环境噪声n(t)之和，即：

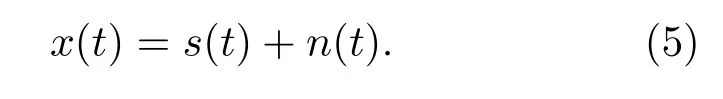
已知STFT为一种线性时频分析方法，因此对接收信号x(t)进行时频分析有

其中，X(m,k)、S(m,k)、V(m,k)分别为被噪声污染的声呐接收信号、纯净信号以及噪声的STFT复数谱，m和k分别为时间帧和频率帧的序号。

X(m,k)包含实部分量Xr(m,k)与虚部分量Xi(m,k)，如式(7)所示：

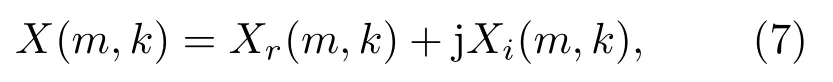
其中，j为虚数单位。

本文建立深度去噪网络完成接收信号STFT谱X到其与纯净信号STFT谱S之差V的映射，获得估计的残差谱，利用残差学习能够加速网络训练并且取得更好的效果。去噪后信号时频谱，如式(8)所示：

图2和图3分别为信噪比或广义信噪比为0 dB情况下脉冲信号时域序列和时频图。可以看出，高斯噪声在时间域和时频域上的分布都较为均匀，脉冲信号特征较为明显。非平稳行船噪声在时间上表现出起伏的特征，此例中中间段信噪比较小，而两端较大，时域图中靠近中间段的脉冲被淹没，而时频域上脉冲特征仍较为明显。α稳定分布噪声某些时刻出现能量较强的脉冲噪声，在时频图上表现为平行于频率轴的亮线，在时域和时频域上信号特征都相对较弱，更难以检测。

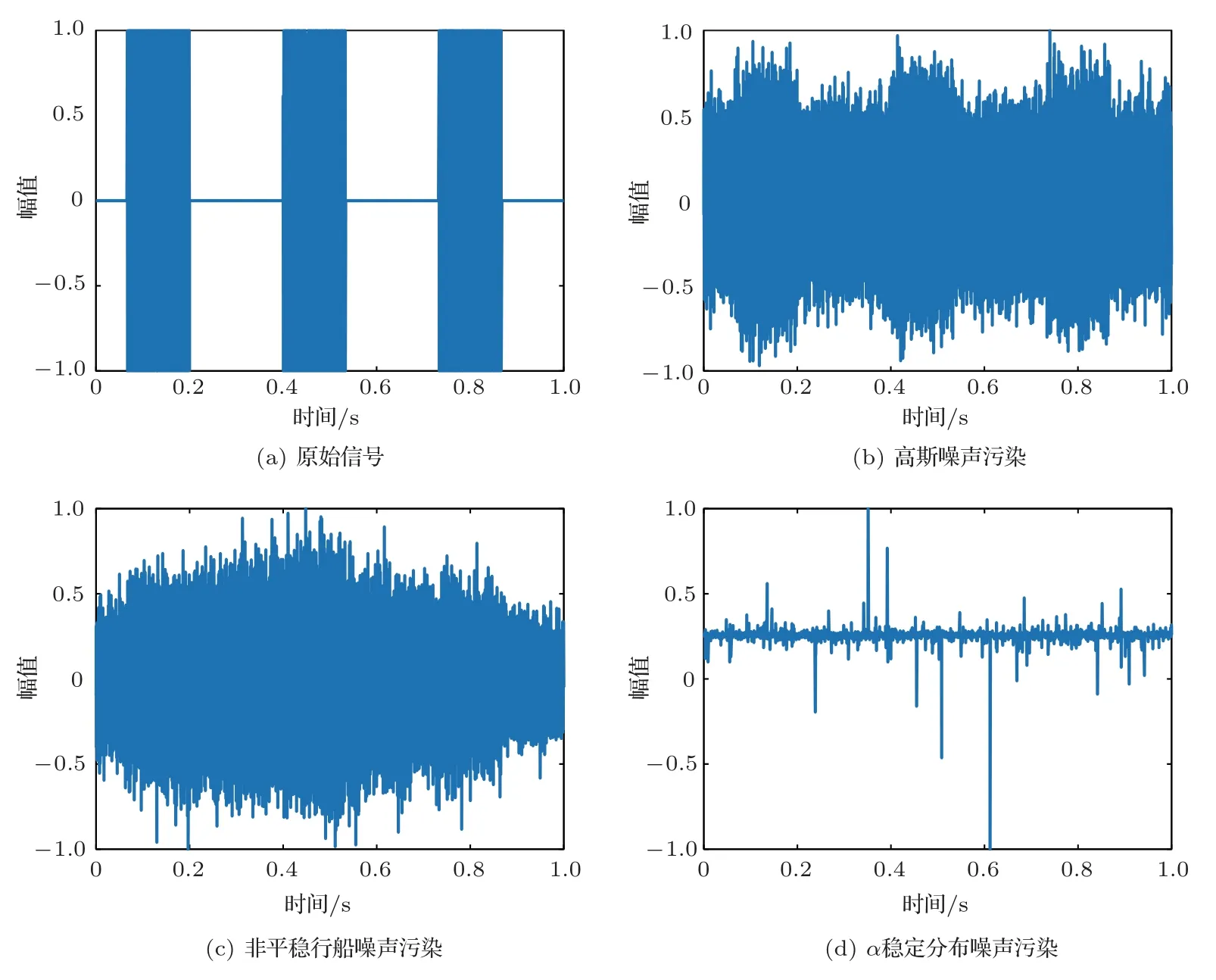
图2 信号时域序列Fig.2 Time-domain sequence of signals

图3 信号时频图Fig.3 Spectrogram of signals

2.2 网络模型与参数设置

本文中脉冲信号去噪网络采用全卷积的网络结构，模型结构如图4所示，参数设置如表1所示。去噪网络共15层，第1层到第14层中各层包含一个卷积层和一个ReLU非线性激活层，最后一层仅包含一个卷积层。除最后一层，各卷积层均采用64个卷积核来提取特征，最后一层的卷积核数目为2，与输出通道数相同。网络输入特征共两个通道，分别为接收信号STFT谱X的实部分量Xr和虚部分量Xi，网络输出特征包括残差信号的实部分量r和虚部分量i。

图4 脉冲信号去噪网络Fig.4 Pulse signal denoising neural network

表1 脉冲信号去噪网络参数设置Table 1 Parameter setting of pulse signal denoising neural network

去噪网络的损失函数如式(10)所示：

其中，M、K分别表示STFT时间帧和频点的总数，B为批大小。

3 仿真实验与分析

此小节利用仿真数据对脉冲信号去噪模型进行训练，并与传统的基于最小均方误差(Least mean square,LMS)的自适应滤波方法进行性能对比。

3.1 仿真数据集

本文的目标是在复杂噪声背景下对脉冲信号进行去噪。实际接收信号中有可能存在多个甚至不同类型的脉冲信号，并且脉冲信号可能出现在任意时刻，处于任意频段。因而在生成仿真数据集时，一条样本中需要仿真一到多个脉冲信号，并且脉冲信号的类型随机产生。为简化问题，将一条样本中含有的脉冲数上限置为2，即一条样本中至多含有两个脉冲信号。脉冲信号的起止时间、起止频率均随机产生。仿真信号各项参数如表2所示。

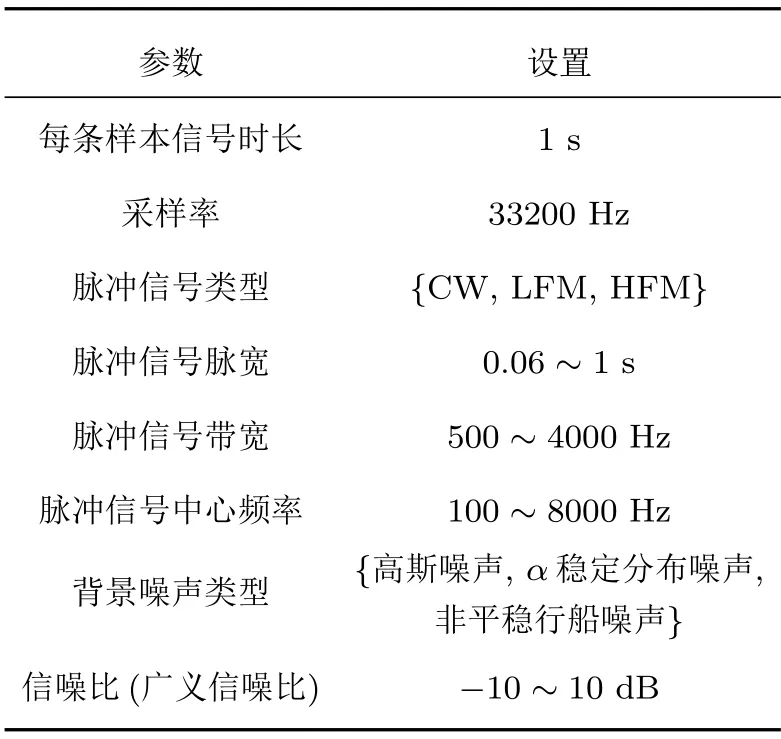
表2 仿真信号数据集参数设置Table 2 Parameter setting of simulation signal data set

对仿真得到的时域样本信号进行STFT，设定窗长为512，窗与窗之间有50%的重叠，去除冗余保存128个频点，因此1 s的数据可以得到128×128×1的三维STFT复数特征。提取STFT谱的实部分量与虚部分量，并归一化，作为网络的输入。在产生仿真数据时，保留纯净信号的时频域特征，将接收信号与纯净信号幅值谱残差作为去噪网络的输出。

仿真数据集包含5000条样本，划分数据集为训练数据集和测试数据集，比例为9:1。

3.2 去噪性能分析

图5(a)和图5(b)分别为测试样本的纯净信号时域序列和时频图，其中包括两条脉冲信号分别为CW信号和LFM信号。图5(c)～图5(h)为纯净信号经过高斯噪声、非平稳船噪声以及α稳定分布噪声污染后的信号时域序列和时频图。

图6展示了经过本文模型去噪与重构后信号的时域序列与时频图，可以看到，在3种噪声条件下，本文模型均能取得较好的去噪结果。尤其是在α稳定分布噪声样本中，对比图5(g)、图5(h)与图6(e)、图6(f)，本文模型去除了α稳定分布噪声中的能量很强的宽带脉冲噪声，增强了目标脉冲信号，极大地提高了信噪比。对时域图进行放大如图7所示，本文模型重构的脉冲信号与原始信号近乎重合，对信号特征保留完整。

图5 仿真测试样本示例Fig.5 Examples of simulation test samples

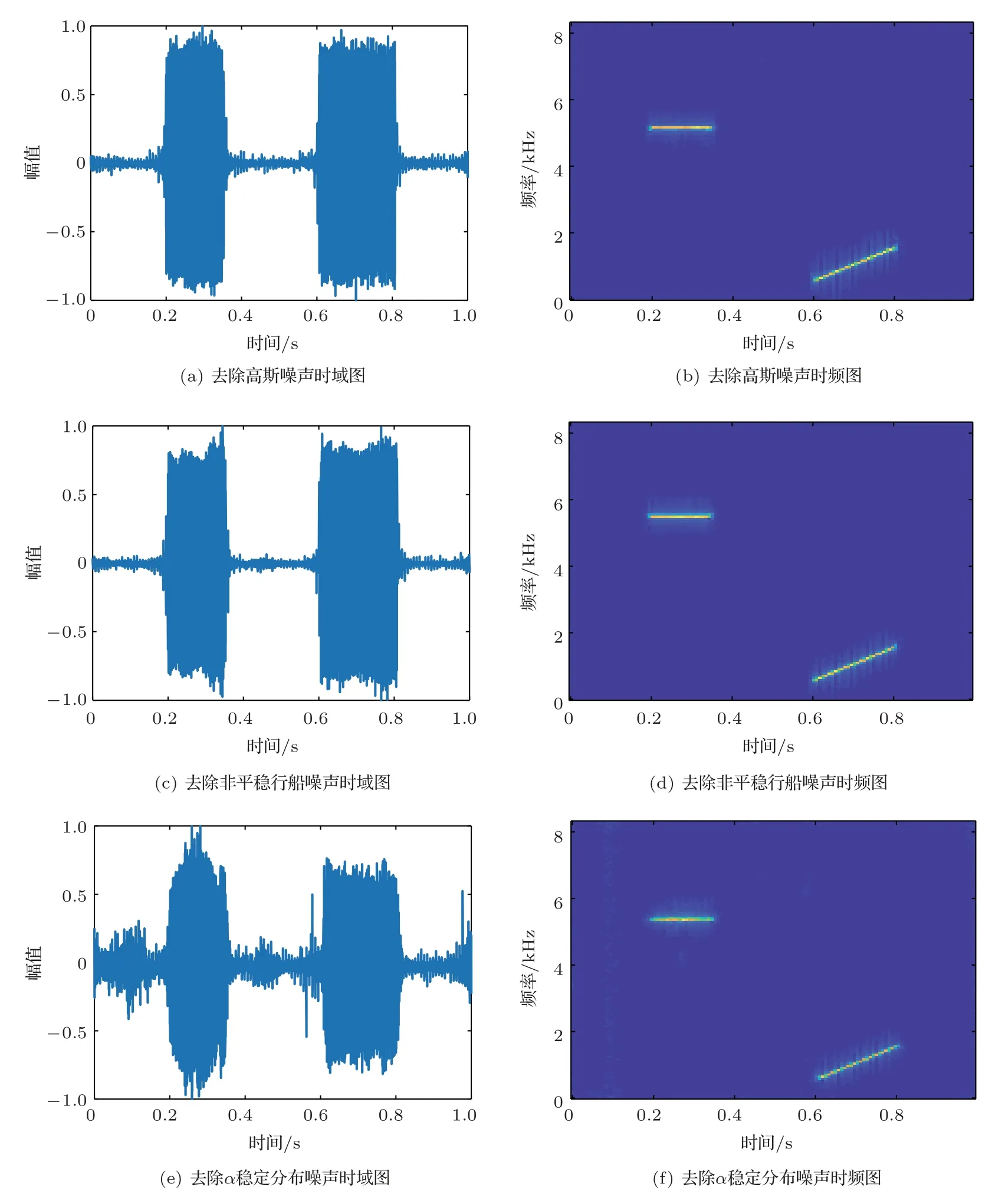
图6 本文模型去噪结果Fig.6 The denoising results of the neural network model

图7 本文方法重构信号时域放大图Fig.7 Zoomed diagrams of signal sequence reconstructed by denoising neural network

图8为LMS滤波方法在高斯噪声和非平稳行船噪声背景下，通过时域滤波获得去噪信号的时域图及其对应的时频图。可以看到，在高斯噪声下，LMS滤波获得的结果尚可接受，图8(c)、图8(d)中，由于背景噪声非平稳，第2个脉冲之后的背景噪声仍然有较多残余。去噪信号时域图中，去噪信号与原始信号差异较大。

图8 LMS滤波去噪结果Fig.8 The denoising results of LMS

图9为LMS滤波在α稳定分布噪声下的去噪结果。可以看到LMS滤波受到强噪声影响较大，与图5(g)、图5(h)进行比较，时域图和时频图上出现的能量较强的信号均为强噪声信号，脉冲信号完全被滤除。主要原因是，LMS滤波是基于二阶统计量的方法，对于α稳定分布噪声下的信号处理失效。

图9 LMS滤波去噪结果Fig.9 The denoising results of LMS

对比本文提出的深度学习去噪方法与传统的LMS滤波方法，本文在3种噪声分布中的去噪性能均优于LMS滤波，能够有效抑制噪声，提升信噪比，并且能够较为完整地重构信号，恢复信号幅度和相位特征，在多种噪声场景中的多种脉冲信号去噪任务中表现出良好的性能和泛化能力。

4 实测数据验证

截取某实验中接收的两段脉冲样本，一条为CW信号，一条为LFM信号，如图10所示。实际实验中，无法获得接收信号的纯净样本，然而由于本次实验的条件较为理想，可以将接收信号近似作为纯净脉冲信号。截取美国国家公园采集的冰川湾水下声响中的“中度风(Moderate Winds)”样本作为环境噪声样本[14]，如图11所示，可以看到此例中的风噪声体现出一定的α稳定分布特性。在实测脉冲中添加噪声，使信噪比为−1 dB，如图12所示，可以看到在时域图中脉冲信号被噪声淹没，待检测的脉冲在时频谱图中能量也相对较弱。经过去噪模型增强，可得到处理后脉冲信号，如图13所示，可以看到非高斯噪声被有效抑制，各个脉冲信号相较处理前被显著增强。对比图13(b)与图10(b)可以看到本文方法增强的信号比截取实测脉冲信号更加纯净，脉冲信号之外时段与频段的噪声分量都得到了有效的抑制。放大重构信号中0.008 s数据，如图14所示，重构后的信号近似贴合截取脉冲。实验结果体现了模型在实测数据上良好的泛化性，预示着良好的应用前景。

图10 实测脉冲信号Fig.10 Actual measured pulses

图11 实测噪声信号Fig.11 Actual measured noise

图12 实测脉冲添加实测噪声Fig.12 Measured pulses add measured noise

图13 本文模型去噪结果Fig.13 The denoising results of the neural network model

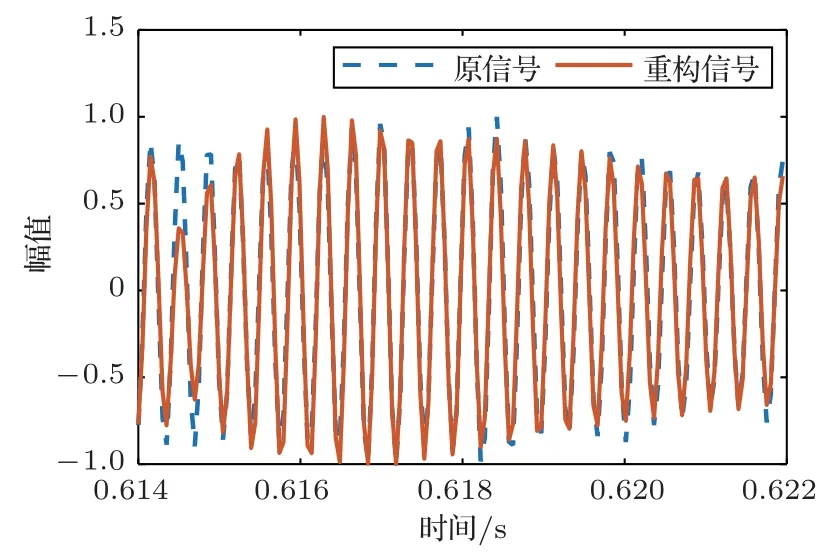
图14 本文方法重构信号时域放大图Fig.14 Zoomed diagram of signal sequence reconstructed by denoising neural network

5 结论

本文提出一种基于深度学习的能够在高斯和非高斯环境噪声中增强与重构水声脉冲信号的方法。通过建立全卷积的脉冲信号去噪模型，学习接收信号STFT特征与接收信号和纯净信号STFT特征残差之间的映射，实现噪声抑制，最后通过逆变换重构脉冲信号。仿真实验结果显示，模型可在3种背景噪声中有效实现脉冲信号的去噪与重构，相较传统的LMS滤波方法获得了更加优越的性能。通过在实测数据上的测试，模型显示了在实测数据上较好的泛化性，体现了一定的工程应用前景。