利用k-Wave计算超声在腹壁组织的声辐射力∗

乔玉配 宫门阳 汪海宾 李楠 刘杰惠 毛一葳 何爱军 刘晓宙

(1 近代声学教育部重点实验室 南京大学声学研究所 人工微结构科学与技术协同创新中心 南京 210093)

(2 江苏科技大学理学院 镇江 212003)

(3 南京大学电子科学与工程学院 南京 210093)

0 引言

声辐射力一般定义为声波对介质施加的周期平均力[1]。声辐射力的研究始于1902年Rayleigh提出“声辐射压”的概念[2]，已经有百年历史[3]。1991年，Wu[4]首先提出了声镊子的概念并进行了实验，实现了利用声辐射力对物体的操控。利用声辐射力不仅可以操控生物细胞和粒子，也可以用于探索内部解剖结构并获取诊断信息。声波属于机械波，利用声辐射力进行的操控对介质的导电性、透光性等没有特殊的要求，可以实现对粒子和生物组织的无创、非接触、无标记、多功能性等操控[5−7]，且其相应的设备简单易集成和微型化，因此，声辐射力在精密制造、精准医疗医学诊断，评估生物组织和液体的黏弹性特性、弹性成像等生物医学领域具有广泛的应用，尤其是在弹性成像领域[8−12]。弹性成像能够获得生物组织的弹性信息，可以检测出生物体内部与周围组织弹性不同的区域，进而根据此差异判断相应组织或器官可能发生的病理改变以及其位置、形状和大小。声辐射力弹性成像是一种新的无创弹性成像方法，是利用声波产生的声辐射力对组织施加压，通过采集组织被激发前后的超声图像进行运动估计，或检测组织在声辐射力终止后不同时间点的应变，或检测声辐射力激发组织而产生的剪切波的传播进行成像来反映生物组织的弹性(或硬度)[13]。因此，声辐射力是弹性成像技术有效性和精确性的关键核心，对其预测和研究至关重要。

数值模拟是计算声辐射力最直接和直观的方法。k-Wave可以用于复杂和真实组织介质中的时域声学和超声模拟，是模拟声辐射力的一种精确而有效的工具。它结合了有限差分法的简单性和在任何非均匀介质中模拟的灵活性，具有快速、易用的特点[14−17]。本文基于腹壁组织图像，利用k-Wave对超声波在腹壁组织区域传播时的声场进行数值模拟，通过模拟得到其声场分布，进而计算求得其声辐射力的分布。

1 理论

声波在介质中传播时，压力、密度、温度、颗粒速度等都会发生动态变化，这些变化可以用一系列基于介质内质量、动量和能量守恒的一阶耦合偏微分方程来描述。当能量足够高的声波在各向异性介质中传播时，声波的传播不再是线性的，其一阶耦合方程组为[17]

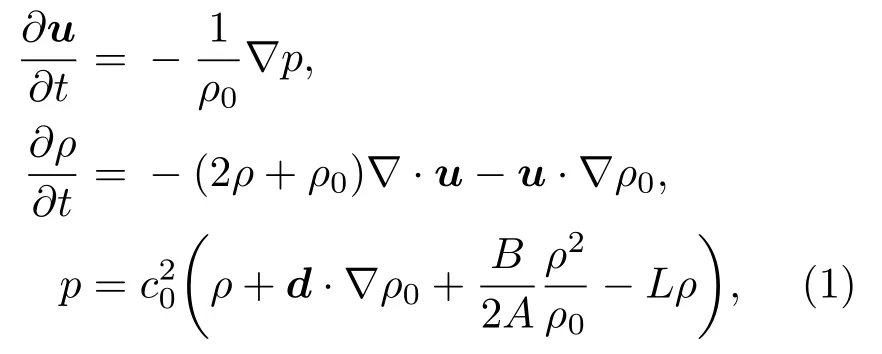
其中，u是介质质点速度，ρ0是介质静态密度，p为声压，ρ是密度，是一个与空间有关的物理量，t为时间，c0是等熵声速，d介质质点位移，B/A为非线性参数，L说明了遵循频率幂律的声学吸收和色散，可以表示[18]其中，τ、η为吸收和色散比例系数，y1为幂律指数。注意，当这些公式作为耦合方程被求解时，u·∇ρ0和d·∇ρ0被取消[19]，因此，为了提高计算效率，这些项不包括在下面给出的离散方程中。

为了减少精确模拟所需的内存和时间步数，k-Wave使用k-space伪谱法离散化耦合声学方程组(1)，空间导数的频谱计算使用快速傅里叶变换，每个声波波长只需要两个网格节点即可达到可接受的精度，能够快速高效地实现生物组织中非线性超声传播的模拟，计算得到其声辐射力。k-Wave中基于k-space伪谱法离散化耦合声学方程组(1)得到其离散形式如下：

式中的Nξ是在ξ方向的网格点数。

方程(3)中的离散方程使用时间步长∆t=CFL∆x/cmax迭代求解，为了能够平衡准确性和计算效率之间的关系，CFL≤c0/cmax。在弱异构介质，通常CFL=0.3能够为精度和计算速度之间提供很好的平衡[19]。在每个时间步长，可以通过在计算域内的适当网格点添加源值来引入质量或力源。类似地，模拟的输出可以通过在特定网格点的每个时间步长记录声学变量来获得。

声辐射力的一般表达式为[14−15,20−21]

式(4)用到扰动分析以及

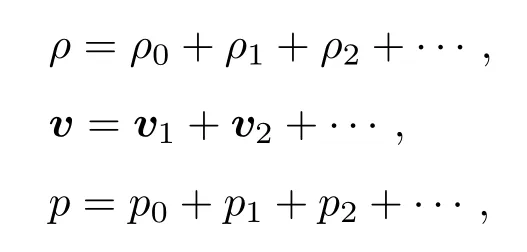
其中，ρ、p、v分别表示介质的密度、声压、质点速度，n为面S的法向矢量，〈〉表示时间平均，下标0、1、2分别代表静态、一阶、二阶微小量。

对于体积元(N/m3)的声辐射力，公式(4)可以表示为

虽然公式(4)和公式(5)是无黏性流体情况得到的，严格地说只适用于在不存在剪切且剪切模量为零的流体中的传播，但它考虑了由黏性衰减和不均匀性可能造成的散射而导致的波动量在封闭面内体积沉积，而且在医学超声应用的实际环境中，软组织具有相当低的吸收和散射特性，组织中的体模量远大于剪切模量，压缩应力比剪切应力更容易出现，因此，公式(4)和公式(5)计算腹壁组织的声辐射力是合理的，对本文的问题仍然适用。基于公式(5)计算的声辐射力所用的声压和质点振速是由k-Wave运算过程中记录的声压和非交错网格中的质点振速。

2 仿真模型的建立

本文的声场是由100个阵元组成的线性相控阵换能器，如图1(a)所示；其相应的物理参数示意图如图1(b)所示。仿真中设置计算区域为(Nx×Ny×Nz)，沿x方向的网格数Nx=88，沿y方向的网格数Ny=108，沿z方向的网格数Nz=44，阵元宽度为1个网格，阵元长度为12个网格，阵元中心距离为0，换能器的中心频率为1MHz，换能器放置在yz平面中间位置，声波沿x方向传播，其聚焦点在x方向距离换能器Nx/2×dx。为了能够保证较高的精度和计算速度取网格大小dx=dy=dz=1.5×10−4m和CFL=0.1。生物组织样品(腹壁组织)放置在声场中，其横截面图如图2所示，包含结缔组织、肌肉、脂肪、水等主要成分，其相应的参数值如表1所示。图2中的Lx=Nx×dx，Ly=Ny×dy，Lz=Nz×dz。另外在仿真计算时在计算区域的周围添加PML边界层来模拟无限大区域。

图1 线阵换能器示意图Fig.1 Schematic of the linear array transducer

图2 组织横截面图[22]Fig.2 Cross-sectional tissue map[22]

表1 组织中各成分对应的参数[22]Table 1 Parameters of comp onents in tissue[22]

3 数值仿真

3.1 有效性验证

为了验证k-Wave计算的正确性，首先利用公式(5)对放置在平面波声场中液体柱的声辐射力进行了仿真计算，并与已有的结果进行对比，液体柱内声速为930 m/s2，其密度为1000 kg/m3[23]，半径为7.5 mm，其声场情况如图3所示。图3(a)为平面波入射示意图，图中的圆表示柱形粒子，从图中可以看出平面波向前传播，遇到液体柱发生散射、折射等现象，从而使液体柱受到声辐射力的作用。图3(b)展示了时间t=40µs时其声场情况，图3(c)则是转化成频域中其声场情况。平面入射频率为0.5 MHz，其余参数设置和文献[24]一致。通过k-Wave计算所得无量纲化声辐射力为0.0039，理论计算为0.0042，误差为7.1%，在可接受范围内，验证了k-Wave计算的正确性。

图3 平面波入射到液体柱时的声场分布Fig.3 Sound field distribution when a plane wave incident on a liquid cylinder

3.2 腹壁中的声辐射力

为了计算生物组织(腹壁)的声辐射力，首先用k-Wave对其声场进行仿真，记录整个空间中的声压以及声速，之后用来计算其声辐射力。仿真模型以及计算中所需信息如第2节所述。仿真得到该组织的归一化声压振幅空间分布如图4(a)～图4(c)所示。图4(a)给出了换能器中心频率分别为1 MHz、3 MHz时，其归一化声压振幅随声波主传播轴x的变化；图4(b)～图4(c)为换能器中心频率为1 MHz、3 MHz时，xy平面内归一化声压振幅分布。另外，为了分析腹壁组织的非均匀性对声场的影响，在图4(d)～图4(f)中给出了均匀介质的归一化声压振幅空间分布作为对比。图4(d)为换能器中心频率为1 MHz、3 MHz时，均匀介质中归一化声压振幅随声波主传播轴x的变化；图4(e)～图4(f)为换能器中心频率为1 MHz、3 MHz时，均匀介质中xy平面内归一化声压振幅分布。从图4中可以看出，声压振幅在聚焦点的位置达到最大值。对比腹壁组织和均匀介质中声场情况可以看出，声波在非均匀介质中传播，由于介质密度和声速等的变化而产生散射、反射等现象。对于同一种组织、不同的频率激发下，产生的声场不同。

图4 腹壁和均匀介质中归一化声压振幅空间分布Fig.4 Spatial distribution of the normalized pressure amplitude in abdominal wall tissue and homogeneous media

在计算声辐射力时，得到了在三维空间网格每个点上的力的3个时变分量，然而，在实际的应用中，仅使用零仰角平面(xy平面)内的力作为输入。该平面是力最大的平面，也是用于实际建立弹性图[15]的平面。因此，基于公式(5)计算得到其声辐射力如图5所示，图中声辐射力采用最大声辐射力进行了归一化。

图5 腹壁组织中归一化声辐射力Fig.5 The normalized acoustic radiation force in abdominal tissue

图5分别为归一化的轴向声辐射力、横向声辐射力以及总声辐射力在xy平面的分布。从此图中可以清楚得知声辐射力的分布和大小，在实际的应用中可以更加有效、快捷地使用声辐射力对生物组织施压，以探测生物体的弹性，从而判断生物体是否发生病变。声辐射力的研究为弹性成像技术奠定了基础，使得弹性成像技术更加精准、高效。

另外也可以通过声辐射力的等值面了解到声辐射力的分布，图6给出了在−20 dB、−10 dB处的声辐射力等值面。由声辐射力等值面可以识别具有相同大小的力的所在位置。通过查看相邻等值线的间距可以大致了解力的大小的分布层次。等值面使声压的分布一面了然。

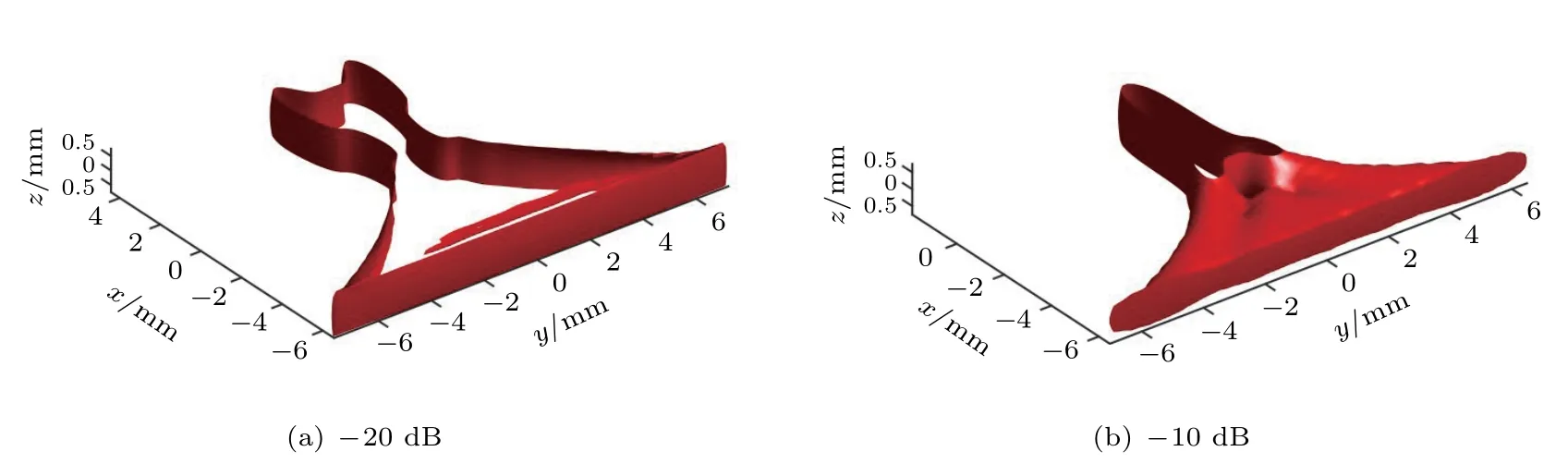
图6 腹壁组织中归一化声辐射力等值面Fig.6 The normalized acoustic radiation force isosurface in abdominal wall tissue

最后对面阵换能器的阵元宽度、间距、阵元个数以及工作频率等参量对声辐射力的影响进行了计算与分析，如图7～10所示。

图7为不同阵元宽度时腹壁组织中沿x方向的归一化声辐射力。图7(a)和图7(b)分别对应阵元间距为0时，不同阵元宽度的轴向和横向声辐射力。为了避免换能器宽度带来的影响，阵元宽度为0.15 mm和0.30 mm时的阵元个数分别取100和50个以保证换能器的宽度相等，此时换能器的宽度都为15 mm。图7(c)和图7(d)分别对应阵元间距为0.15 mm时，不同阵元宽度的轴向和横向声辐射力。同样的，对阵元宽度为0.15 mm和0.30 mm时的阵元个数分别取30和20个以保证换能器的宽度相等，对应的换能器的宽度都为9 mm。从图7可以看出，换能器宽度不变的情况下，阵元间距为0时，阵元宽度对声辐射力几乎没有影响。阵元间距为0.15 mm时，随着阵元宽度的增大，声辐射力变大。这是因为，在阵元间距为0时，不管怎么改变阵元的宽度，面阵换能器实际起作用的面的范围没有改变，其激励下产生的声场没有改变。当阵元之间有间距时，随着阵元宽度的增大，换能器实际起作用的面的范围变大，其激励下产生的声场强度变大，从而使得组织所受的声辐射力增大。

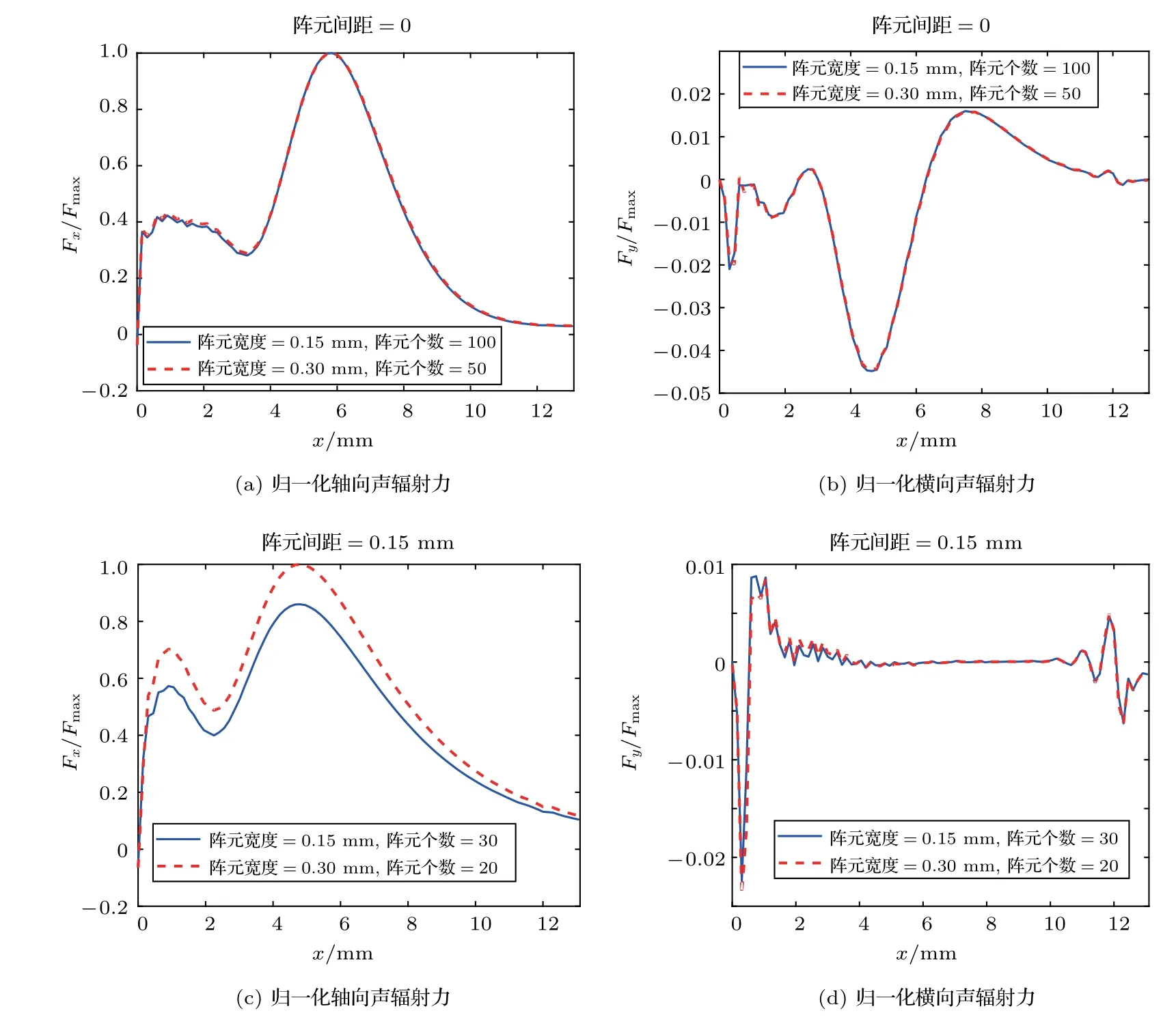
图7 不同阵元宽度时腹壁组织中沿x方向的归一化声辐射力Fig.7 The normalized acoustic radiation force on abdominal wall tissue with different element widths along x direction

图8为不同阵元间距时腹壁组织中沿x方向的归一化声辐射力。图8(a)和图8(b)分别对应阵元宽度为0.15 mm时，不同阵元间距的轴向和横向声辐射力。阵元间距为0和0.15 mm时的阵元个数分别取100和50个以保证换能器的宽度相等，此时换能器的宽度都为15 mm。从图8可以看出，随着阵元间距的变大，轴向声辐射力变小，横向声辐射力变大。

图8 不同阵元间距时腹壁组织中沿x方向的归一化声辐射力Fig.8 The normalized acoustic radiation force on abdominal tissue with different element spacing along x direction

图9为不同阵元个数时腹壁组织中沿x方向的归一化声辐射力。图9(a)和图9(b)分别对应阵元间距为0、阵元宽度为0.15 mm时，阵元个数取100和50个时对应的轴向和横向声辐射力。从图9可以看出，阵元个数的改变使得声辐射力出现峰值的位置发生了偏移。这是由于在阵元间距和宽度不变的情况下，随着阵元个数的改变，换能器宽度发生了改变，使得声场分布发生改变，从而导致声辐射力分布发生改变。

图9 不同阵元个数时腹壁组织中沿x方向的归一化声辐射力Fig.9 The normalized acoustic radiation force on abdominal wall tissue with different number of elements along x direction

图10为不同中心频率时腹壁组织中沿x方向的归一化声辐射力。图10(a)和图10(b)分别对应阵元间距为0、阵元宽度为0.15 mm时，阵元个数为100、频率为2 MHz和3 MHz时对应的轴向和横向声辐射力。从图10可以看出，换能器工作频率不同，声辐射力的大小不同。这是因为不同工作频率的换能器激发的声场强度不同。

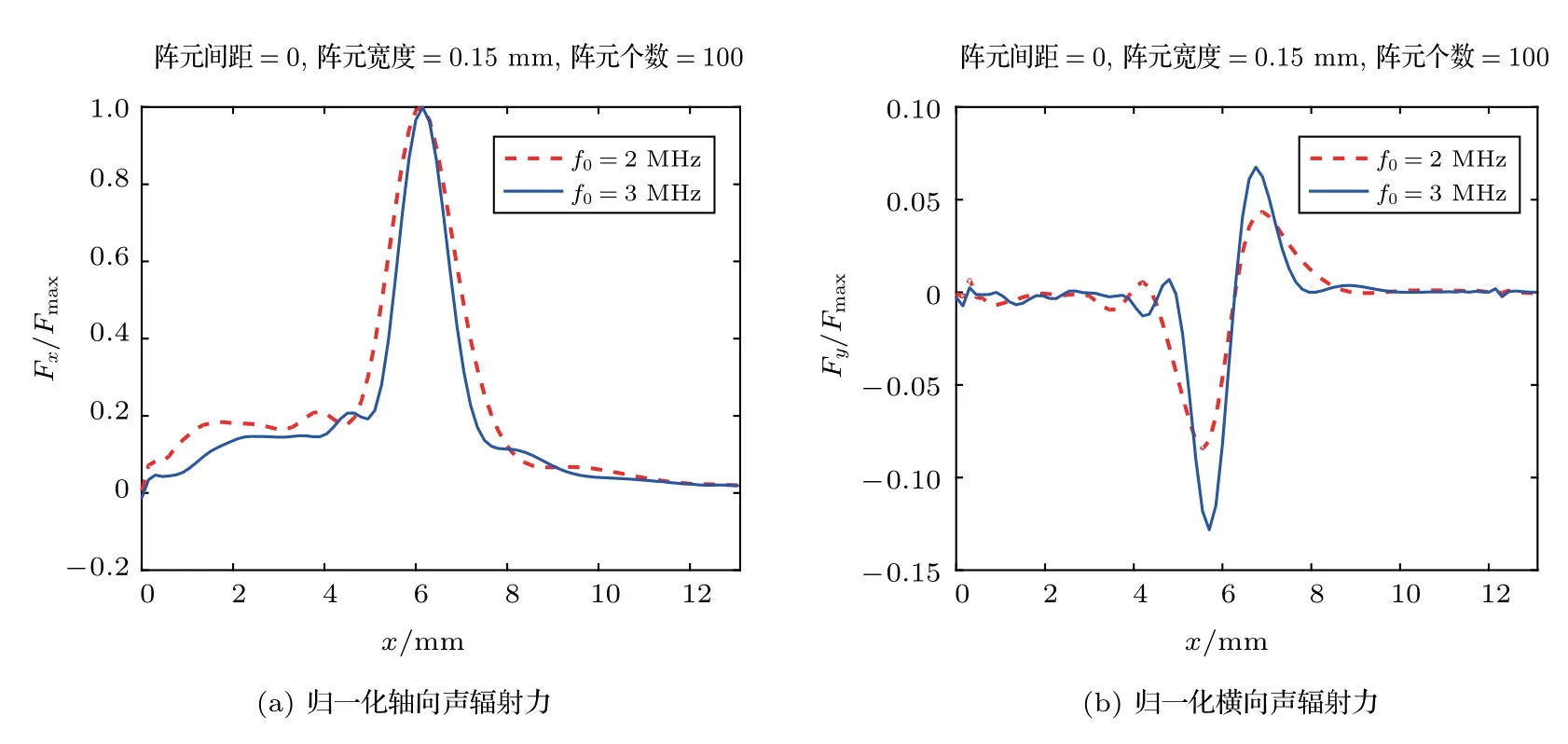
图10 不同中心频率时腹壁组织中沿x方向的归一化声辐射力Fig.10 Thenormalized acoustic radiation forceon abdominal tissuewith different center frequencies along x direction

从以上分析可知，在声辐射力弹性成像中，可以根据需求对阵换能器的阵元宽度、间距、阵元个数以及工作频率等参量进行调节，从而使该弹性成像技术更加精确、高效。

4 结论

利用声辐射力对粒子和生物组织的无创、非接触、多功能性等的操控是一项具有实际应用前景的技术，尤其是在弹性成像领域。分析操控需求，预测相应的声辐射力大小和分布使其应用技术更高效、精确。数值模拟是计算声辐射力最直接和直观的方法。而k-Wave可以用于复杂和真实组织介质中的时域声学和超声模拟，是模拟声辐射力的一种精确而有效的工具。它结合了有限差分法的简单性和在任何非均匀介质中模拟的灵活性，具有快速、易用的特点。本文基于腹壁组织图像，利用k-Wave对超声波在腹壁组织区域传播时的声场进行数值模拟，得到其声场和声辐射力的分布。对面阵换能器的阵元宽度、间距、阵元个数以及工作频率等参量对声辐射力的影响进行了计算与分析，在声辐射力弹性成像中可以按实际需要进行选择和调整这些参量，使该弹性成像技术更加精确、高效。本文研究为声辐射力在弹性成像技术中的应用奠定了基础，为实现精密制造和精准医疗提供核心技术支持。