运用画图策略发展学生推理能力

（晋江市内坑教委办，福建晋江 362200）

推理能力体现在以敏锐的思考分析、快捷的反应、迅速地掌握问题的核心，在最短时间内作出合理正确的选择。《义务教育数学课程标准（2011 年版）》明确指出，应将推理能力作为学生综合能力发展的一项核心任务，并在整个教学进程中注重学生推理能力的培养。推理既是数学学习的内容，也是思考的方式。［1］由于小学生的思维正处于以具体形象思维为主，逐步向抽象逻辑思维过渡的阶段，这决定了发展学生推理能力需要利用画图策略。许多数学问题，可以借助画线段图、列表格、画平面图或立体图形等策略，架“桥”铺“路”，直观地帮助学生理解数学知识，沟通知识的前后联系，充分思考与表达，感悟数学思想方法。

一、清晰理解题意

除了数学本身的逻辑特点，让学生感觉抽象难以理解外，更多的是与数学问题的呈现方式相关。许多数学问题的表述虽然简洁，但多以纯文字的方式呈现，枯燥乏味，且有的题目数量关系比较隐蔽，导致学生常常不能理解题意。根据小学生爱涂鸦的天性，从低年级开始，注重让学生画一画，借助图形、线段、符号等图像表征，弥补文字描述无法呈现或难以清晰呈现的思考路径，使学生读懂、理解题意。这是解决数字问题的关键，也是培养学生推理能力的前提。

例如，教学三年级上册《里程表（二）》一课时（见图1），针对很多学生把160 千米当作是星期一一天行驶的里程数，将表格中的每个数据理解为每天行驶的里程数这一情况，设计以下教学环节：

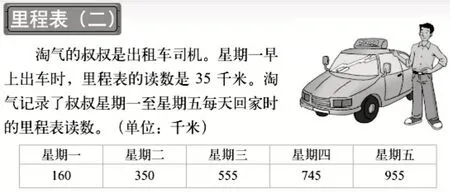
图1

师：160 千米是星期一一天行驶的里程数吗？

生1：表格中的数据表示淘气的叔叔星期一当天的里程数为160 千米，如果将其理解为当天行驶了160 千米，是错误的。

师：两种表述有什么区别？

生1：星期一的里程数是160 千米，不仅包括星期一当天行驶的里程数，还应该包括星期一出车前的35千米。若理解为星期一当天行驶了160 千米，则表示他当天行驶的里程为160 千米。

师：是不是有点难以理解？你能画图说明吗？

师：小宣同学画了线段图（见图2），谁看懂了？

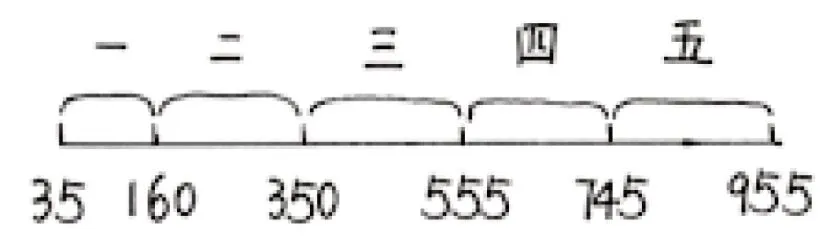
图2

生2：我看懂了。这样画图，我们就能很清楚地知道，35 千米是星期一出发前的读数，不是星期一这一天行驶的，160 千米是包括星期一出发前与星期一当天在内的里程数，而星期一当天的里程数的计算列式为：160-35=125（千米）。

生3：我也看懂了。比如星期四的745 千米里，包含了前面的里程数，要将星期四当天的里程数计算出来，则列式为：745-555=190（千米）。

师：这道题一开始不好理解，画了线段图后，就能清楚理解题目的意思，画图这种方法真实用。

直观图的应用价值广泛，能把隐性的数学关系显性化，使抽象的文字形象化。当数学问题不易理解时，可以让学生画图，把文字信息“画”成图形信息，用“图”将数量关系直观、形象地体现出来，帮助筛选有用信息，理解题目意思，找到解决问题的策略，起到支撑和辅助学生分析和理解抽象数学知识的作用。

二、沟通知识联系

小学数学的教材内容是按不同层次，分知识领域、分板块单元编排的，各版块之间既有纵向发展的知识体系，又有横向的联系与拓展，呈现出纵横相连的网状结构。教学中，不能仅停留于教会学生掌握某个知识点，还要引导学生弄清知识点的前引后伸，沟通理解知识之间的内在联系，才能真正把握数学知识的本质。通过画图，可以直观地对比，打通知识的联系通道，让数学知识串点成线，联结成块，帮助学生形成系统的知识结构，从而发展推理能力。

例如，教学“0.2×3=？”时，得出计算结果后，教师追问：“0.2×3=0.6 这个结果是怎么算的？”学生经过思考，从不同的角度展示各自的计算方法：

①0.2×3 表示3 个0.2 相加，0.2+0.2+0.2=0.6（乘法的意义）

②0.2 元=2 角，2×3=6 角，6 角=0.6 元（借助人民币换算，转化为整数）

③0.1×2×3=0.6（数一数有几个相同的计数单位）

④（0.2×10）×3÷10=0.6（积的变化规律）

⑤画图理解（见图3）

图3

“仔细观察，这些方法之间有什么联系吗？”教师继续追问，不仅仅停留在展示交流环节就结束教学。通过画思维导图（见图4），启发学生思考知识之间的关联，找到知识之间的本质共性，对这些方法进行对比、分析和梳理。“乘法的意义、积的变化规律、运算律”，都是基于对“运算的意义”方面来解决问题的；用“单位换算、计数单位、分数”这些方法，是基于对“数的认识”；而画图则更加直观，融合了这两种认识。

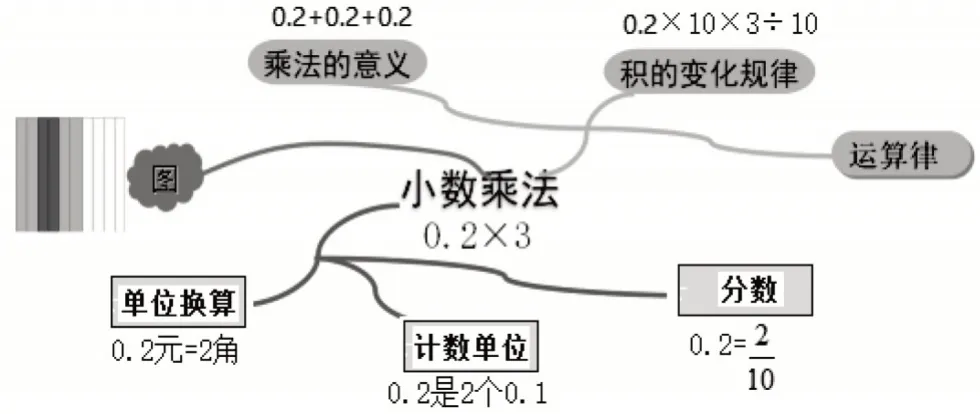
图4

借助思维导图，学生体会到，这些不同的方法都体现“数一数有多少个这样相同的计数单位”这个数学本质。这样“画龙点睛”，让学生的思维渐趋渐明，知识脉络直观清晰，从而真正深刻地理解小数乘以整数的意义，也为小数乘法的后续学习提供丰富的研究经验。“知识联通”，直指数学知识的本源，有利于学生将知识结构化，进一步促进推理能力的提升。

三、有序思考表达

曹培英认为，思维习惯会影响推理能力。若遇到问题后，学生做到有理有据的推测与思索，那么首先会以语言等多种表述形式，将自己所思考的内容进行表达。小学生的数学思维具有明显的形象性，在表达的思维过程时，往往缺乏条理性和层次性，不能扣紧本质，不能将自己的想法作清晰完整的数学表达。通过画图，为学生搭建表达的脚手架，结合规范的数学表达句式，可帮助学生轻松直观地分析问题，做到表述的准确、完整与有条理，逐步提高学生的逻辑表达与推理能力。

例如，“鸡兔同笼，有9 个头，26 条腿，问鸡兔各几只？”这一问题，对于大部分学生来说比较抽象，特别是用假设法解答时，很多学生更是云里雾里，不知所云。如果让学生列表格、画图形，给予充分的表达交流的时间，就会呈现不一样的精彩。

1.列表格，在有序思考中推理表达

①将鸡或兔按“从少到多”或者“从多到少”的按顺序来列表（见表1），只需几步就知道鸡和兔各有几只。②列表的过程中，关注数据的变化情况，是否存在什么规律？引导学生充分意识到，每增加1 只鸡，兔的数量则减少1 只，总腿数则减少2 条的数量变化，根据规律，对数据进行适当调整。③让学生充分地表达推理、思考的过程。

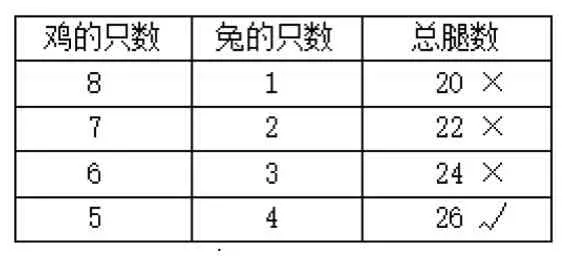
表1

2.画图形，借助关联句式，完整表达推理过程

①选取有代表性的图形进行表达交流。鸡兔总共9 只，可用简单的图形代替鸡兔的头和腿，如用圆圈“○”表示头，用竖线“|”表示腿。②推理表达时，尽量使用推理的关联句式，完整地表达思考推理的过程。［2］如使用“先……再……”“如果……那么……”“根据……可以……”“因为……所以……”等关联句式进行数学表达：

生：我先画9 个圆圈表示9 个头，每只配上2 条腿看鸡，还剩8 条腿，再把每只鸡添上2 条腿变成兔，8 条腿可以换4 只兔，一看图就得到一共有4 只兔和5 只鸡（见图5）。

图5

生：如果把1 只鸡和1 只兔看作一组，一组一组地画，画到4 只鸡和4 只兔时，还剩下1 个头2 条腿，那么剩下的就是1 只鸡，所以总共有5 只鸡和4 只兔。（见图6）

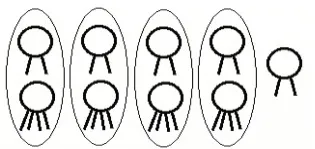
图6

借助画“图”和丰富的数学语言，引导学生把“动手画、动口说”有机结合起来，用清晰的数学语言，有条理地表述获取知识的思维过程，实现多种形态数学语言的自然转换与不断抽象，以“说”促“思”，培养和发展学生的推理能力。

四、感悟推理思想

在数学知识学习过程中，进行推理思想的渗透，进而发展学生的推理能力，是数学教育的重要任务之一。若将数学知识看成是一条明线，推理思想则是数学知识中隐藏的暗线，需要学生通过思维进行分析与感悟，才能将其找出。教师如果能够运用画图策略，引导学生直观感悟，长期不断地渗透，有利于帮助学生形成良好的推理习惯。

例如，教学二年级上册“6 的乘法口诀”前，通过前测，发现大部分学生都已经知道6×7=42，能背诵“六七四十二”的口诀，但对“为什么6 乘7 得42”的道理解释不是很清晰。基于此，可借助“点子图”，让学生在圈一圈、画一画中感悟算理。

1.设问：6×7=42，你能借助点子图“圈一圈”，说明这句口诀表示的意义吗？学生呈现思考过程（见图7）：［3］

图7

2.对比：观察这些不同的圈法，你有什么发现？①都是表示7 个6，都把7 个6 分成几个6 相加。不同的是，有的分成两部分，有的分成三部分。②都是将新口诀转变为旧口诀来辅助计算。

3.小结：通过圈一圈、画一画，得到“六七四十二”这句口诀，这样把新知识变成以前学过的知识，利用旧知学习新知的方法叫作“转化”，是数学学习中重要的思想方法（板书：新知—转化—旧知）。

该教学模式的应用，将数学的几大要素（口诀、图形与公式）等彼此衔接，让乘法口诀涵盖的内容更丰富，学生对口诀意义也产生更全面深入的了解。在寻找新旧口诀联系的过程中，渗透“转化”这一推理思想，也为今后学习乘法分配律奠定了扎实的基础。