形式三角矩阵半环的导子与高阶导子*

张源野， 谭宜家

(福州大学数学与计算机科学学院,350108,福建省福州市)

0 引 言

半环理论是代数理论研究的一个重要内容，应用很广泛[1,2].半环上的导子是半环理论中的重要研究内容之一[3-5].1993年，Coelho和Milies[6]证明了C-代数A上的上三角矩阵环的导子可以表示成一个内导子和一个A上C- 导子诱导的导子之和.2006年，谢乐平和曹佑安研究了形式三角矩阵环上的导子,给出了形式三角矩阵环上导子的结构形式[7]；2013年，Lu等学者研究了形式三角矩阵环上的高阶导子,给出了形式三角矩阵环上高阶导子的结构形式[8].

三角矩阵环、形式三角矩阵环都是特殊的形式三角矩阵半环.本文在上述基础上进一步研究形式三角矩阵半环的导子和高阶导子,证明了三角矩阵半环Tri(R,M,S)的任一导子可由半环R,S的导子和(R,S)-双半模M的一个拟同态来表示；半环Tri(R,M,S)的任一高阶导子可由半环R,S的高阶导子和(R,S)-双半模M中满足一定条件的一族可加映射来表示.

1 基本概念

定义1.1[1]一个半环是一个代数系统(R,+,·),其中(R,+)是一个带有恒等元0的交换幺半群,(R,·)是一个带有恒等元1R的幺半群,乘法对加法满足左右分配律.同时,对于任意a∈R,0a=a0=0.0≠1R,元素0,1R分别称为半环R的零元和单位元.

一个半环R称为加法可消半环[1]，如果对于任意a,b,c∈R,由a+b=a+c可推出b=c.

设(R,+,0)是一个交换幺半群,a∈R.a称为可反的,如果存在b∈R,使得a+b=0,此时b称为a的一个反元.不难验证,如果元素a有一个反元,那么这个反元是唯一的,a的反元记为-a.如果a,b∈R,且b是可反元,我们定义a-b=a+(-b).不难验证,对于半环R中的任意元a,b,如果b是可反元，那么a(-b)=-ab，(-b)a=-ba.显然，一个半环R是一个环当且仅当R的每一个元都是可反元.

半环是丰富的.例如,每一个带有单位元的环是一个加法可消半环；每一个布尔代数、每一个有界分配格都是半环；又如，整数环Z(有理数域Q,实数域R)的正锥Z0(Q0，R0)是一个加法可消半环；再如Max-Plus 代数 (R∪{-∞},max,+)[9]是一个半环.

定义1.2[1]半环R上的一个左半模(简称左R-半模)是一个交换幺半群(M,+,0)，并且存在一个映射R×M→M，(r,m)→rm，满足对于任意r,r′∈R,m,m′∈M，均有

(1)r(m+m′)=rm+rm′； (2)(r+r′)m=rm+r′m； (3)(rr′)m=r(r′m)；

(4)1Rm=m； (5)r0=0=0m.

类似地，可定义半环S的右S-半模.一个交换半群(M,+)如果既是左R-半模又是右S-半模，并且∀a∈R,m∈M,b∈S，均有(am)b=a(mb)，则称M为(R,S)-双半模.

定义1.3[1]设R是一个半环，d：R→R是一个映射.d称为R的一个可加映射,如果对于任意x,y∈R,均有d(x+y)=d(x)+d(y)；d称为R的一个导子,如果d为R的一个可加映射，并且对于任意x,y∈R,均有d(xy)=d(x)y+xd(y).

注1.1 不难验证,对于半环R的任意一个导子d,均有d(0)=0.

定义1.4 设R,S是两个半环，M是(R,S)-双半模.dR,dS分别是R,S的导子,f：M→M是一个映射.f称为双半模M的一个(dR,dS)-拟同态,如果f是M的可加映射，并且对于任意r∈R,m∈M,s∈S,均有f(rm)=dR(r)m+rf(m),f(ms)=f(m)s+mdS(s).

定义1.5[10]设R,S是两个半环，M是(R,S)-双半模,则集合

在通常的矩阵加法和乘法下构成一个半环，称之为形式三角矩阵半环.

2 导 子

(2.1)

证明充分性.通过直接计算可得d是半环Tri(R,M,S)的一个导子.

必要性.设d是Tri(R,M,S)的任一导子.对于任意x,y∈Tri(R,M,S),设

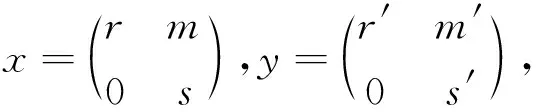
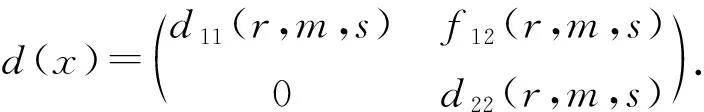
(2.2)

(2.3)

d11(0,m,s)=0.

(2.4)

d11(r,m,s)=d11(r,0,0)+d11(0,m,s)=d11(r,0,0).

(2.5)

式(2.5)说明d11(r,m,s)不依赖于m与s．类似可证d22(r,m,s)不依赖于r与m．

现将d11(r,m,s)和d22(r,m,s)分别记为dR(r)和dS(s)，于是得到两个映射dR:R→R和dS:S→S．下证映射dR:R→R与dS:S→S分别是半环R与S的导子.

由式(2.2),得

dR(r+r′)=dR(r)+dR(r′),dS(s+s′)=dS(s)+dS(s′),

由式(2.3),得

dR(rr′)=dR(r)r′+rdR(r′),dS(ss′)=dS(s)s′+sdS(s′)．

所以dR与dS分别为半环R与S的导子.于是dR(0)=0,dS(0)=0(根据注1.1)．这样式(2.3)变为

(2.6)

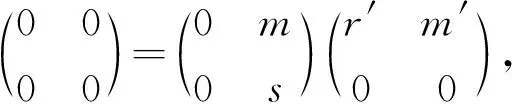
记m1=f12(1R,0,0),则m1是M的可反元,且f12(0,0,1S)=-m1.

f12(r,0,0)=rf12(1R,0,0)=rm1.

(2.7)

f12(0,0,s)=f12(0,0,1S)s=-m1s.

(2.8)

由式(2.2)，(2.7)，(2.8),得

f12(r,m,s)=f12(r,0,0)+f12(0,m,0)+f12(0,0,s)=rm1-m1s+f12(0,m,0).

记f12(0,m,0)=f(m)，那么得到映射f:M→M,并且f12(r,m,s)=rm1-m1s+f(m).所以

下证f:M→M是(R,S)-双半模M的一个(dR,dS)-拟同态.

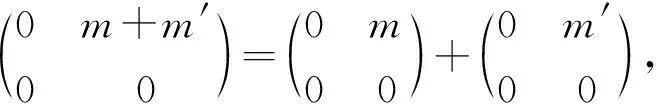
f(m+m′)=f(m)+f(m′).

f(rm)=f12(0,rm,0)=dR(r)m+rf12(0,m,0)=dR(r)m+rf(m).

类似可证f(ms)=f(m)s+mdS(s).所以f是M的一个(dR,dS)-拟同态.证毕.

3 高阶导子

定义3.1[11]设R是一个半环,D={dn|n∈}是R到自身的一族可加映射.D称为R的一个高阶导子,如果对于任意n∈与任意x,y∈R,均有

其中d0表示R的恒等映射IR,表示非负整数集.

引理3.1 设R是一个半环,D={dn|n∈}是R的一个高阶导子.那么

(1)对于任意n∈,dn(0)=0；

(2)如果R是加法可消的,那么对于任意正整数n,dn(1R)=0.

证明(1)当n=0时,d0(0)=IR(0)=0,结论成立.假设对于小于n,(n≥1),时结论成立.那么对于n,由归纳假设,知

(2) 当n=1时,d1(1R)=d1(1R1R)=d1(1R)1R+1Rd1(1R)=d1(1R)+d1(1R).由于R是加法可消的,所以d1(1R)=0.

假设对于小于n,(n≥2),时结论成立.那么对于n,由归纳假设,知

因为R是加法可消的,所以dn(1R)=0.

定理3.1 设R，S是两个加法可消半环，M为(R,S)-双半模,D={dn|n∈}是形式三角矩阵半环Tri(R,M,S)到自身的一族映射.那么D是Tri(R,M,S)的高阶导子当且仅当存在R的高阶导子}，S的高阶导子},(R,S)-双半模M的一族可加映射F={fn|n∈}以及M中的一族可反元M0={mn|n是正整数}，使得对于任意n∈,均有

(3.1)

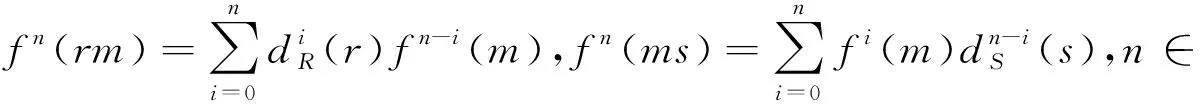
证明充分性.通过直接计算可得D是半环Tri(R,M,S)的一个高阶导子.

必要性.设D={dn|n∈}是Tri(R,M,S)的高阶导子.

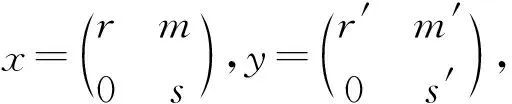
(3.2)

(3.3)

(3.4)

(3.5)

(3.6)

(3.7)

为了证明必要性,我们先用归纳法证明.

对于任意n∈，不依赖于m与不依赖于r与m．

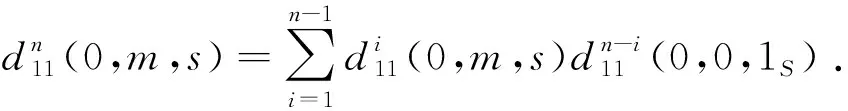
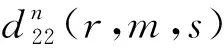
对于任意n∈，将记为将记为则得到映射和

于是,对于任意n∈，由式(3.7)，得

(3.8)

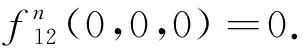
在式(3.8)中,令r=1R,r′=0,m=m′=0,s=0,s′=1S，由引理3.1(2)得

在式(3.8)中,令r′=1R,m′=0,s′=0，由引理3.1(1)得

(3.9)

类似地,在式(3.8)中,令r=0,m=0,s=1S，得

(3.10)

由式(3.4),(3.9),(3.10),得

(3.11)

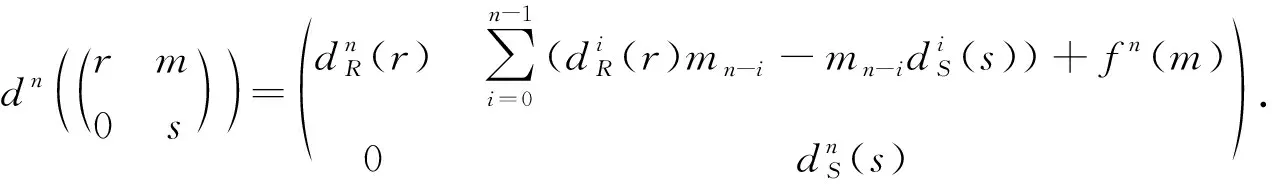
下证fn:M→M是可加映射且满足对于任意r∈R,m∈M,s∈S，均有

首先,在式(3.4)中,令r=r′=0,s=s′=0，得fn(m+m′)=fn(m)+fn(m′).