基于距离离群点数据挖掘技术的防窃电算法研究

陈永健

(仰恩大学 福建泉州 362014)

在经济由高速向高质量发展的今天，居民生产生活及制造业用电量日益激增，稳定的电力供应保障支撑着社会正常的经济秩序。但是，科技的发展也让窃电技术更为隐蔽，窃电种类和手段层出不穷。据现有数据统计，每年全国因窃电造成的经济损失至少达200万亿以上[1]，不仅严重影响了我国电量供应质量和电量营销管理模式，也危及了社会经济秩序的正常运行。目前，根据窃电原理分析，主要的窃电种类包括与计量设备有关的欠电压欠电流法、扩差法、移相法和与计量设备无关的私自增容、改装计量表、绕越计量表等窃电方式。与计量设备有关的窃电手段较为突出，传统的基于分类算法、决策树算法和单纯式离群点检测算法很难准确地锁定窃电用户。离群点数据挖掘技术原本应用于股票等金融市场，在防窃电领域的应用已经成为新的研究热点，具有广泛的研究价值[2]。本算法的核心是利用电量波动率进行数据分析并采用距离算法的离群点挖掘技术，该算法有效地解决了程超等[3]单纯采用离群点算法存在的计算量复杂、准确率不高，且只适用于欠电压、欠电流窃电法的问题。

1 距离离群点挖掘算法模型

距离离群点数据挖掘是在大量的用电量数据中剔除不符合窃电实际异常偏高的数据，根据质心的确定按一定规则自动选取数据的过程。假定有一个N个对象的数据集或知识集X，写作X(N)。期望的对象离群点数为K，从数据集X中剔除不利数据后确定质心N0，必能找到与质心存在显著不同的数据K0。算法模型归纳为两个概念：距离离群点和距离离群点的数据挖掘方法。

定义1 在电量数据集对象X中,以质心N0为基准参照距离，存在第K个对象使得距离D(K)与D(N0)的距离最大，X(K)为距离离群点。

如果对电量数据集中所有对象X进行归一化数据变换，至少存在部分对象X(X∈[0，1])与对象Y的距离大于D，那么对象Y就是基于距离D的离群点。反之，必然存在有(1-X)个对象与对象Y距离小于D。

离群点数据挖掘方法应用于防窃电领域在现有文献资料中主要有5种：基于决策树的数据挖掘[4]，对采集的数据要进行重复扫描、排序、处理，数据算法效率低；基于簇的数据挖掘[5]，适用场合有限，需要定义簇平均值，对分类属性不适合；基于距离离群点数据挖掘[6]，解决经典K均值算法未考虑孤立点问题，孤立点正是基于距离的，是在给定的数据集中自动找出与均值距离最大的点，但此算法数据计算量大；基于SVM向量机数据挖掘[7]，多应用于多维数据算法，比较复杂；基于K近邻分类数据挖掘[8]，对采集样品的容量相差较大时不适合，而且计算量很大。因此，综合以上5种数据挖掘方法，本算法先对采集的数据进行电量波动率分析处理，转化为一维数据，再运用离群点数据挖掘算法，让算法更加简便高效。

2 距离离群点挖掘算法分析

2.1 电量数据变换

对采集用户的用电量数据一般用电量波动模型进行分析，通过电量波动率找出与用户日用电量之间的特征关系。研究用电量数据集合之间的关系即数据波动情况，一般用方差、方均根值、标准偏差[9]等方法进行描述。其中，标准偏差在描述数据离散程度中应用最多。标准偏差法对于采集同一样本的电量数据,在不同时间下的波动情况很难做出比较。此外，当采集的样本初值不一样，均值不相同，这样也无法比较它们的离散程度。因为本算法是要在不同时间或日期下对采集的电量数据进行比较，确定波动率大小，用标准偏差法显然无法实现。因此，本算法提出了一种新的电量波动描述方法，即利用变异系数CV[10](Coefficient of Variation)对采集数据进行变换形成界于(0，1)区间的一维简化数据，并用它来描述电量波动的离散程度，这种方法巧妙地化解了以上难题。

(1)

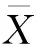
通过大量数据采集与现场排查比对得出：CV<20%时，电量波动处于合理区间；20%≤CV≤50%时，为正常允许范围内；50%80%时，疑似高度窃电行为，需进行入户排查。CV变异系数(离散系数)一般是用来分析平均值不同的数学问题，广泛应用于股票、基金等金融市场指数算法[11]。目前应用于电力领域的研究比较少，本文通过大量数据采集分析计算变异系数，并结合不同用户的类型设置合理的波动范围，验证了窃电识别算法的准确性与高效性。

2.2 分析算法原理

距离离群点数据挖掘算法原理是对采集的用户电量数据首先按一定规则进行清洗和处理，接下来对筛选下来的数据再按电量波动模型确定离群点。最后，计算离群点两两之间的距离来判断不同数据对象之间的近似程度。距离越大的，两者相似度就低；距离越小的，两者相似度就高。

采集用户的日用电量数据组成数组A{y1,y2,...,yn},显然，A是一个一维数组，判断数组中对象之间的相似程度用距离来描述，因此，数组A所有数据间的距离用相似度矩阵来表示：

(2)

图1 电量波动模型距离离群点的检测流程

式(2)中，Dij表示第i和j个数据之间的距离，dij=|yi-yj|≥0，且dij=dji，dji趋近于0时，数据间的相似度高；dji偏离0越大，相似度就越低。同时，距离矩阵以对角线为基准具有对称性。通过对称矩阵确定距离离群点后，建立电量波动模型，计算电量波动率对离群点进行挖掘。电量波动模型距离离群点的检测流程如图1。

电量数据处理并不是简单地剔除不利数据或异常数据，而是要进行数据预处理和清洗，即对数据属性不完整、异常偏高、负值等进行剔除，然后，对电量数据进行归一化处理。

每天的实际用电功率计算方法：

Pi'=Pi-Pi-1

，

(3)

式(3)中，Pi'为某一天的实际用电功率，即正向有功功率。由于电表功率累积计算，当天的用电功率为当天的抄表数减前一天的抄表数。

可见，对于规模化数据直接利用正向有功功率数值，不利于算法处理，为简化算法分析对所有采集处理的数据进行归一化处理[12-13]。

(4)

式(4)中，G(i)归一处理后的电量数据在0～1之间，minP(n)为数据处理后的最小数，max(P(n))为数据处理后的最大数。

图2 距离离群点算法流程图

定义3 比例系数K用来体现存在不合理数据的个数对变异系数的影响程度。K取值过大会误剔除部分有用数据影响算法的精度，K取值过小未能全部剔除不合理数据导致算法误差大，在计算质心时K的合理取值应为1.2，K的不同取值影响变异系数如下：

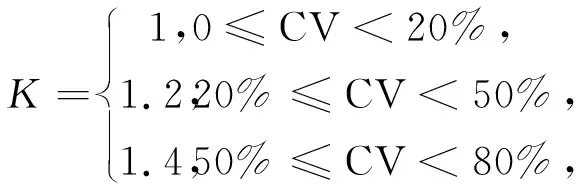
(5)

式(5)表明当CV≥0.8时，说明电量数据波动率远远超过允许范围，这种情况可直接进行现场窃电检查。这证明了引入电量波动率能够更加有效地提高离群点检测效率。

电量波动率质心确定后，下一步就是进行距离离群点算法分析，图2为距离离群点算法流程图。图2中，寻优参数α可调，即可以控制输出结果在一定的范围内。假设A≤α≤B，在这个范围内可以设置α=A+0.01λ，λ为寻优次数，由上限值A和下限值B确定。本算法流程中，λ是自动循环寻优的次数，通过循环寻优可获取距离离群点的挖掘数据，窃电嫌疑对象也就是最优挖掘对象，即最优的α值。

3 仿真分析

3.1 MATLAB仿真

t/d 图3 某纺织公司上半年计量有功数据

为验证本算法在实际窃电检测中的准确性，建立MATLAB仿真。首先对电力公司用电信息采集的数据按一定规则进行清洗处理，下面以福建晋江某纺织公司为例。该公司2018年1～6月共183 d实际用量数据如图3所示。图中计量功率反应了该公司上半年用电量的真实数据，计量功率随着公司每天的用电量累计增加，当公司处于正常的生产用电时曲线趋向于一条直线，斜率也基本上趋于固定。如果公司存在窃电行为，某一天或某一段时间计量功率必然减小，导致该时间段曲线的斜率下降。因此，仅从计量功率曲线很难准确判断公司半年内是否存在窃电行为，或者哪一天存在窃电行为。

为准确锁定窃电数据，判定窃电时间，下面运用本算法对采集数据进行窃电分析。首先，根据公式(3)计算每天的用量功率数据。如图4所示，圆点带黑色填充的数据就是利用电量波动率计算欧式距离检测出来的离群点。可见，离群点在距离上明显区别于大部分点，在所有数据中只占一小部分，这与“距离离群点”的定义相符合，从欧式距离很明显地被区分出来。

t/d 图4 算法分析前的离群点检测结果

t/d 图5 算法分析后的离群点检测结果

根据定义2的计算方法可得出该公司1～6月的电量波动率：CV1=0.028，CV2=0.192，CV3=0.186，CV4=0.557，CV5=0.179，CV6=0.185。可见1月份的波动率最小，2、3、5、6月波动率都小于20%，数据都比较平稳，只有4月份波动率超过50%。

再通过质心计算并结合公式(5)计算可得出CVmax=0.557,K=1.2,剔除不利数据前的质心avg1=48.955，剔除不利数据后的质心avg2=44.886，因此，质心avg2更能代表数据的整体水平，证明了质心选择的合理性。

图4为未进行算法分析前的离群点检测，因为并未考虑窃电行为，所以会造成用电量比正常值偏低。异常高于质心的点在本算法中不具有现实意义，干扰算法分析，在分析计算前应先将这部分异常离群点剔除。图5是进行算法分析后的离群点检测，离群点集中于4月底，检测结果与先前1～6月的电量波动率计算结果相吻合。从图5可知，离群点检测结果符合窃电原理，4月的电量波动率最大，出现窃电的可能性也最大。本算法检测的窃电时间点正是出现在4月，证明了离群点检测的准确性。可见，采用电量波动模型的距离离群点检测与其他窃电检测方法相比具有简便高效的优势。

在仿真过程中，考虑到实际用电过程中1～2 d时间数据异常并不能确定为窃电行为，可能是某些特殊原因(如停电)等造成。因此，在算法分析过程中增加了窃电报警条件判别，可以根据需要设置第3天为连续窃电报警，这样筛选后的离群点与最终的结果一致，如图5所示。需要指出的是，仿真过程中寻优参数α取0.866，至少存在K=0.866×183≈158个数据与离群点之间的距离D(K)大于D(N0)(D(N0)=8.256)，符合定义1所规定，说明检测的离群点可信度比较高。

3.2 验证算法检测结果

本算法的检测结果可以为一线稽查人员提供入户排查的理论依据，根据这一结果帮助排查人员快速锁定窃电嫌疑用户和具体窃电时间。

如表1所示，以下是应用本算法和常见的3类防窃电算法检测结果与实际稽查结果比较，数据结论对比证明了应用本算法进行窃电检测达到的准确度较为理想。为便于比较，分别采集了纺织厂、机加工厂和酒店等10家公司半年内的数据进行分析。结果表明，当算法判别度大于60%或低于50%时，算法分析结果与实际稽查结果一致；当算法判别度介于50%～60%时，仅出现一组数据与稽查结果不一致，判别准确度达到90%。在表1中，同样用这10个公司上半年的用电量数据应用单纯的离群点算法准确度为80%，决策树和分类算法准确度都为70%，可见，上述3种算法的误报率和漏报率相对偏高，证明本算法判别准确度有明显优势，相比较至少提高了10%以上。实验证明，通过电量波动率下的质心计算方法，再增加或细化数据的采集量，比如采集一整年以上的数据或增加窃电分析对象的数量，更能精确锁定代表大部分数据的质心点。然后，在距离离群点算法中增加自动寻优次数λ，更能准确锁定离群点，这样解决了算法判别度介于50%～60%时出现误报的问题，进一步提高本算法的准确度，达到更好的窃电判别效果。

表1 不同窃电算法判别与实际稽查结果对比

4 结论

本文提出一种基于距离离群点数据挖掘技术的防窃电算法模型，该模型结合电量波动率进行数据分析，是针对用户用电量信息的新的窃电判别方法。此算法提出利用变异系数来描述电量波动率，再根据电量波动率计算质心点，通过质心与离群点的定义应用欧氏距离计算筛选出距离离群点，从大量数据中挖掘出窃电嫌疑对象。本算法把复杂的数据处理简单化，分析效率高，不同于其他仅仅依靠离群点定义来筛选的离群点算法，也不同于传统依靠电压、电流、相位等参数来判别窃电的算法。尽管本算法解决了其他窃电算法计算量复杂、效率不高、判别准确度低等问题，但该算法仍然存在缺点，即筛选离群点的寻优参数调节次数有限，对于规模化数据处理，寻优参数不能达到最优，因此算法模型有待进一步改善。