运载火箭POGO主动抑制的LQR控制器设计

赵旺 刘锦凡 谭述君 毛玉明 吴志刚

运载火箭POGO主动抑制的LQR控制器设计

赵旺1,2刘锦凡3谭述君1,2毛玉明3吴志刚1

（1 大连理工大学工业装备结构分析国家重点实验室，大连，116023；2 大连理工大学辽宁省空天飞行器前沿技术重点实验室，大连，116023；3 上海宇航系统工程研究所，上海 201109）

针对传统蓄压器难以满足大型捆绑火箭的Pogo抑制要求的问题，本文提出了基于LQR控制器设计的Pogo主动抑制方法。以采用低温液氧／煤油补燃循环发动机的某运载火箭为研究对象，建立了Pogo主动控制单元模型，导出了Pogo控制系统的状态空间模型；以泵入口压强最小为指标，设计了LQR全状态反馈控制器和部分状态反馈控制器，实现运载火箭Pogo振动的主动抑制；进而研究了控制器尺寸及安装位置对控制效果的影响。最后通过对某型号运载火箭Pogo主动抑制设计的稳定性分析和时域仿真，表明所设计的Pogo主动抑制器有效地提高了系统阻尼、抑制了Pogo振动，对模型偏差具有很强的鲁棒性，优于传统的蓄压器设计；并且对控制器尺寸和安装位置不敏感，有利于工程实现。

Pogo振动；稳定性；主动抑制；LQR；鲁棒性

0 引言

Pogo振动问题由来已久，最早出在“大力神－双子座”的无人飞行中[1]，在1960年~1962年间的Thor/Agena和Titan II上出现之后，命名为Pogo[2]，是著名的液体运载火箭振动问题。其产生机理一般认为是发动机产生的随机振动，激起结构的纵向振动，而结构振动又会进一步导致输送管路的液体压力脉动，进一步使推力产生脉动，推力脉动再加剧结构振动的一个正反馈过程[3]。推进系统和结构系统都不是造成这一结果的原因，而问题的根源是这两系统的相互作用[2]。Pogo振动问题使运载火箭的安全性和可靠性受到很大的威胁，不但会对人体造成伤害，甚至会导致发射失败[4]。Titan II[2]、Titan Ⅲ、Delta、Thor/Agena[5]、Saturn V[6]和中国的CZ－2F[1]等运载火箭以及航天飞机[7]都出现过不同程度的Pogo振动现象。

对于Pogo抑制问题，传统的方法是在泵入口处设置蓄压器，通过设计蓄压器的参数使其达到最佳的状态[8]。国外火箭多采用注气式蓄压器[9-10]，而我国一般采用贮气式蓄压器[11-15]。针对各种蓄压器的抑制效果，国内外学者开展了大量的研究[16-18]。但是不论哪种蓄压器，都属于被动控制措施[19]。随着航天技术的发展，运载火箭规模越来越大[19]，特别是捆绑火箭的出现，箭体的结构动力学特性变得越加复杂，一方面箭体出现低频的密集模态，另一方面大量的模态呈空间分布，在纵横扭方向上均存在明显的投影，结构的纵向、横向和扭转模态都有可能与推进系统耦合而引起振动不稳定。传统膜盒蓄压器无法满足大型捆绑火箭的Pogo抑制要求[19]，一方面其柔性在飞行过程中不可调，无法满足火箭在不同飞行时刻对蓄压器的变柔性要求；另一方面受结构设计的限制，其气腔的工作容积和工作压力不能太大，当膜盒压缩量较大时，膜盒刚度会急剧增大，这会降低蓄压器的实际柔度，变频降幅能力受到一定限制，严重限制了Pogo振动的抑制效果。随着大型液体捆绑火箭技术的发展，需要一种能够满足空间分布模态，有效频率范围宽，并且随时间可调的Pogo抑制方式。

Pogo主动抑制作为不同于蓄压器的抑制方法，最早在航天飞机研制中被提出[20]，Lock和Rubin[21]等人考虑了各种主动抑制系统设计在航天飞机系统中的应用，论证了Pogo主动抑制理念的可行性，并基于LQR控制，设计了针对航天飞机的Pogo主动抑制器[8]。但是上述研究仅是针对航天飞机。国内，胡久辉等[20]使用“积分+PI控制”的方法进行Pogo主动抑制，有效的提高Pogo系统的结构阻尼比，实现系统稳定。本文以采用低温液氧／煤油补燃循环发动机的某运载火箭为研究对象，进行主动Pogo抑制设计。为更好地描述Pogo特性，本文结合先进的状态方程建模方法，建立了主动控制单元模型，并以泵入口压强最小为指标，设计LQR控制器，通过仿真分析了控制器效果。最后，还研究了控制器尺寸及安装位置对控制效果的影响，获得相应的规律性研究结果。

1 液体火箭POGO控制模型

1.1 推进系统

推进系统可分为传统推进系统单元部分与三通—控制器单元部分，其中三通—控制器单元采用“改进Rubin”[23]的思想建模，它的推导及建立是本节的重点。

1） 传统推进系统单元

传统推进系统采用改进的Rubin模型，这部分包括：贮箱、可压缩管、可压缩管—五通、预压泵、泵、泵后管—阀门、燃气系统和气—液型推力室。其中贮箱、可压缩管、可压缩管—五通、预压泵、泵、泵后管—阀门等属于传统推进系统单元中的液路部分。这些单元需要建立状态空间模型，写成相应的二阶状态空间方程的形式。推导过程在文献[23]中已经给出，本文不再赘述，直接给出上述单元的动力学方程。

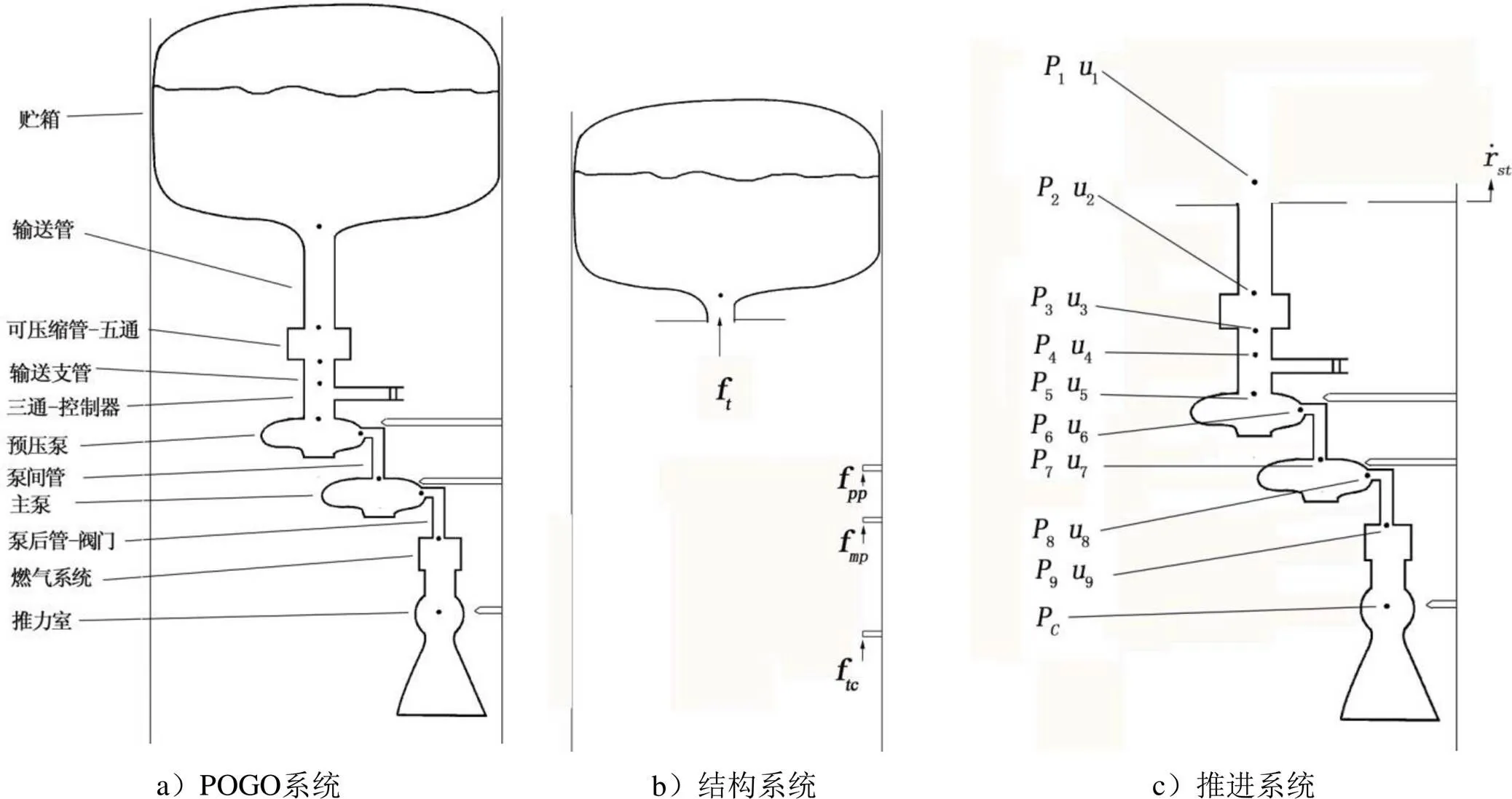
图1 Pogo回路示意图

贮箱单元的动力学方程如式（1）所示

可压缩管-五通的动力学方程如式（2）所示

预压泵的动力学方如程式（3）所示

泵的动力学方程如式（4）所示

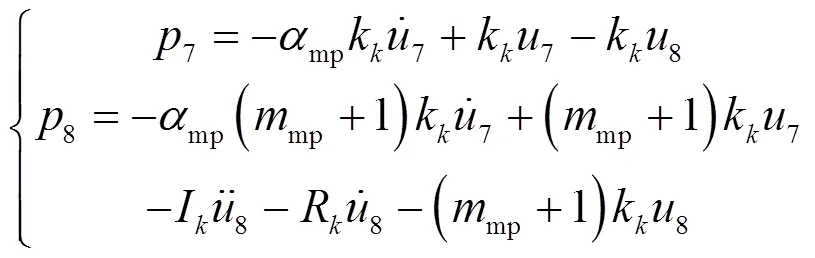
泵后管—阀门的动力学方程如式（5）所示

输送管、输送支管、泵间管等单元的动力学方程如式（6）所示，他们均属于可压缩管，因此动力学方程的形式相同

除液路部分外，传统推进系统单元还有燃气系统和气—液型推力室，燃气系统包括预燃室、燃气导管和涡轮等组件，根据文献[20]，燃气系统和气—液型推力室可分别简化为

2）三通-控制器单元

由Pogo振动的机理可知，推进系统中的流量脉动是造成耦合不稳定的主要因素，文献[21]指出，Pogo振动可以通过在泵入口处安装主动抑制器得到有效抑制。本文在预压泵入口处设计控制器，以一定的幅度和相位向推进系统注入流量，通过改变推进系统特性进而改善耦合系统稳定性。这与文献[20]中的控制器原理是相同的，本文给出的控制单元示意图如图2所示。

图2 三通-控制器超单元

由于推进系统各单元均采用状态方程法建模，为了将控制器单元纳入状态方程法描述的推进系统中，需导出控制器的状态方程模型。本文采用“改进Rubin模型”的建模思想[23]，首先建立三通和控制管路的动力学方程，然后将三通和控制管路结合构成超单元“三通-控制器”，作为主动抑制装置的控制单元。推导过程如下，建立三通的动力学方程如式（9）、（10）所示

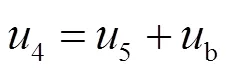
与三通相连的控制管路为可压缩管，它的动力学方程如式（11）、（12）所示

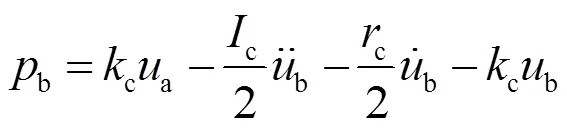
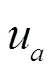
1.2 结构系统

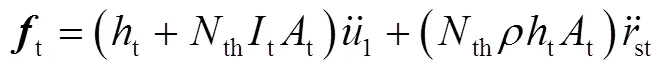
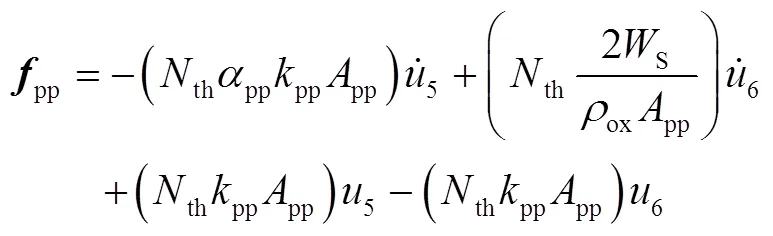
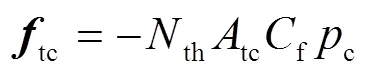
1.3 Pogo控制系统模型

2 LQR控制器设计

本节首先介绍LQR控制器设计原理，然后介绍Pogo系统的LQR控制器设计。

标准的控制系统状态方程可写为下式的形式

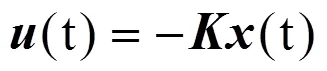
使得下列二次型控制性能指标达到最小值

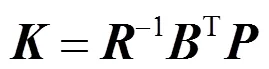
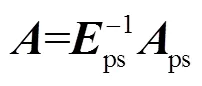
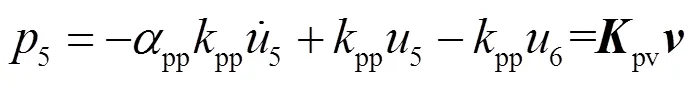
将式（26）代入式（25），即得到（22）式所示的标准形式

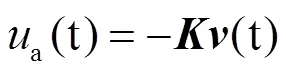
3 仿真与讨论

本节以某型号运载火箭第2秒点的Pogo模型为研究对象，选取合适的控制参数来设计LQR控制器，采用全部状态进行反馈构成全状态反馈控制器；并根据设计结果，保留主要反馈增益值的部分状态进行反馈，构成更加简洁的部分状态反馈控制器。通过稳定性分析和时域仿真来验证LQR控制器效果和有效性。最后简单讨论控制器管路的尺寸及安装位置对Pogo主动抑制效果的影响。

3.1 控制器设计

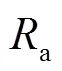
计算式（29）的广义特征值，系统特征值可以由闭环系统的阻尼比和频率表示为式（30）所示的形式

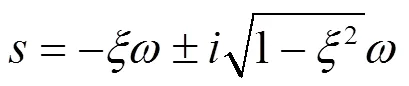
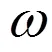
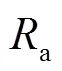
其中第13、14、15、42和43号状态分别代表：氧预压泵入口管入口处的脉动位移，氧预压泵入口处的脉动位移，氧预压泵出口处的脉动位移，结构第1阶模态位移，结构第2阶模态位移。

图3 控制参数R对阻尼比的影响

Fig.3 The influence of parameter R on damping ratio

图4 Ra=1011时的状态反馈增益

3.2 控制器效果分析

图5(a)和(b)给出了不同结构模态质量偏差下，未控时、采取被动抑制器（蓄压器）和主动抑制器（全状态反馈控制和部分状态反馈控制）对结构第1阶和第2阶阻尼比的控制效果。可以看出，模型偏差没有使第2阶结构阻尼比变小，主要使结构第1阶阻尼比变小。未控时Pogo系统的结构第1阶阻尼比随着结构质量模态偏差增大而逐渐降低为负的阻尼比，意味着Pogo系统逐渐失稳；而主动抑制控制器与蓄压器都显著提高了结构系统的第1阶阻尼比，但是提高程度各不相同：全状态反馈器提高结构第1阶阻尼比的程度最高，部分状态反馈控制器次之，蓄压器最差，这体现了所设计的Pogo主动抑制器的优越性。蓄压器虽然相比未控时显著提高了结构第1阶阻尼比，但是随着偏差的增大系统阻尼比明显下降并逐渐失稳，说明蓄压器的鲁棒性较差；而主动抑制控制器作用下，从第1阶阻尼比随着偏差的增大而增大可以看出，系统并没有出现失稳的趋势，体现了Pogo主动抑制很好的鲁棒性。

图5 第2秒点偏差模型控制效果

阻尼比分析结果显示，当结构模态质量为原模态质量1/10时，结构第1阶阻尼比已经降低为负阻尼比，即出现Pogo现象。我们对此时的模型进行时域仿真验证。当全状态反馈控制器作用时，Pogo系统的结构第1阶与第2阶模态位移响应的仿真结果图6和图7所示；当部分状态反馈控制器作用时，结构第1阶与第2阶模态位移响应的仿真结果如图8和图9所示。

图6 全状态反馈控制下结构第1阶模态位移响应

图7 全状态反馈控制下结构第2阶模态位移响应

由图6和图7可以看出，未控时第1阶结构模态位移响应幅值随时间增长而逐渐发散，第2阶模态没有发散；当全状态反馈控制器作用于系统时，结构第1阶模态位移响应幅值明显收敛，结构第2阶模态位移响应振幅大大减小。

可以看出，当部分状态反馈控制器作用时，与全状态反馈控制时相比，结构第1、2阶模态位移响应在降幅效果上略有下降，但是Pogo现象仍然得到有效的抑制，此时结构第1阶模态位移响应幅值明显收敛，第2阶模态位移响应幅值仍明显下降，这也说明了部分状态反馈控制在工程实现上是可行的。而阻尼比分析结果也显示了系统在全状态反馈控制和部分状态反馈控制的作用下都能趋于稳定，且全状态反馈控制的效果优于部分状态反馈控制，时域仿真结果与阻尼比分析结果一致，验证了阻尼比分析结果的正确性，说明全状态反馈控制与部分状态反馈控制是有效的。

图8 部分状态反馈控制下结构第1阶模态位移响应

图9 部分状态反馈控制下结构第2阶模态位移响应

3.3 控制器管路尺寸及安装位置的影响

下面讨论控制器安装位置对控制效果的影响。将控制器安装在推进系统中不同的位置，观察控制器位置的变化对Pogo系统的影响。其中安装位置用数字1-8表示，代表8个不同的安装位置，分别为：贮箱后，第一段管路后，第二段管路后，5通后，输送支管后（原位置），预压泵后，泵间管后，主泵后。结构阻尼比随控制器安装位置的变化如图11所示。可以看出，控制器的安装位置对Pogo系统结构阻尼比几乎没有什么影响，只有从位置4（5通后）到位置5（输送支管后）有细微变化。这说明所设计的Pogo主动抑制器对安装位置不敏感。

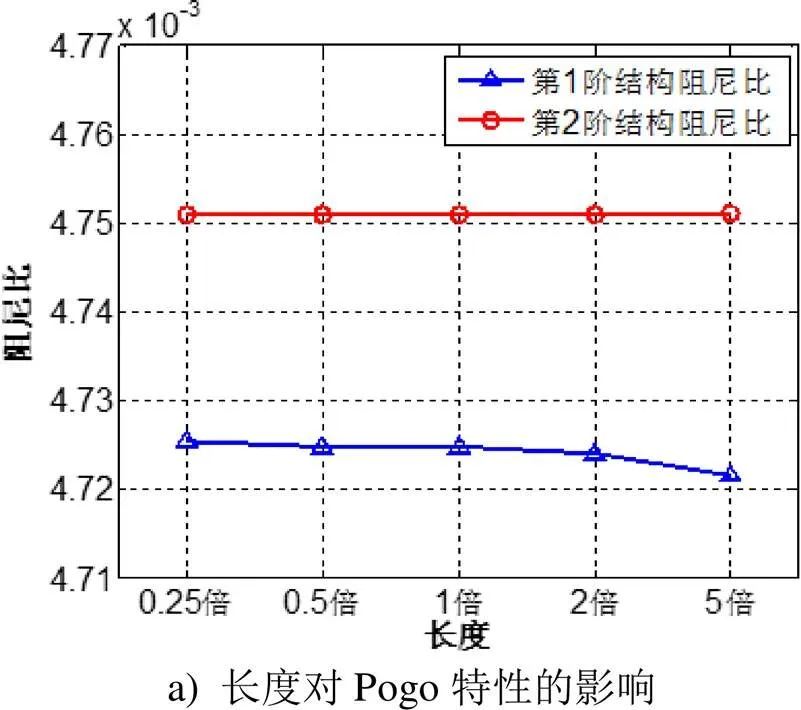
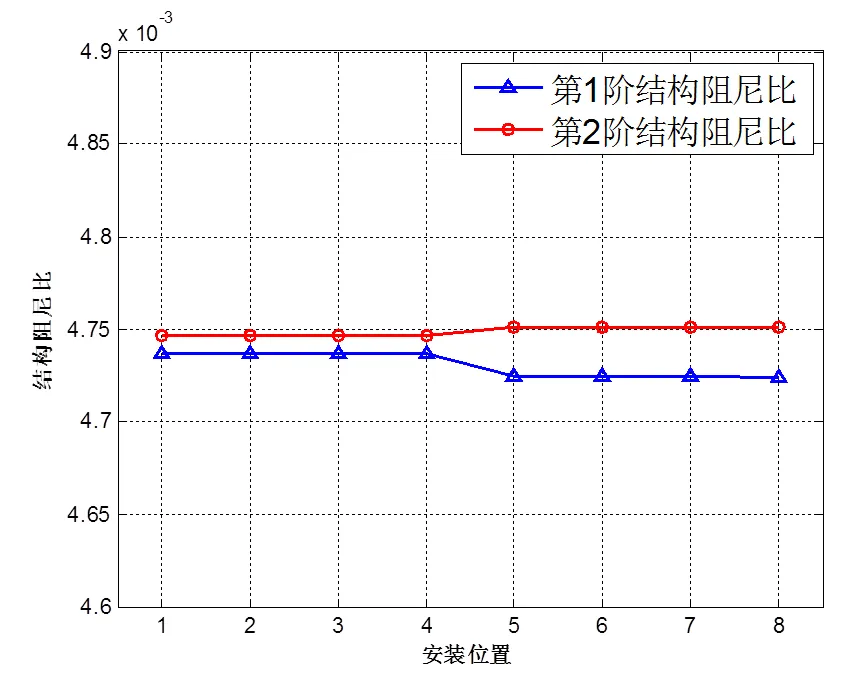
图11 Pogo系统结构阻尼比随控制器安装位置的变化

综合以上分析，主动抑制控制器的尺寸及安装位置对Pogo主动抑制效果的影响不明显，非常有利于工程应用。

4 结论

本文以液氧煤油补燃循环发动机的某型运载火箭为研究对象，建立了主动控制单元模型，从而导出了Pogo控制系统的动力学模型，并选取泵入口流量最小为指标，设计LQR控制器，采用稳定性分析和时域仿真对控制器效果进行了验证，进一步研究了控制器尺寸及安装位置对控制效果的影响。主要结论如下

1）以泵入口流量最小为指标设计的LQR全状态反馈控制器与部分状态反馈控制器对Pogo主动抑制是有效的。

2）所设计的全状态反馈控制器效果最好，部分状态反馈控制器次之，都优于传统的蓄压器抑制效果，对模型偏差具有很强的鲁棒性。

3）所设计的LQR主动抑制器具有一定的工程可实现性。首先主动抑制控制器的尺寸及安装位置对Pogo抑制效果的影响不明显，此外本文提出了只提取关键的状态变量设计部分状态控制器的方法，并验证了这种方法有效性，这些都有利于工程实现和应用。而工程实现中的难点主要是状态变量的获取。对于这一问题，Kalman滤波可以作为获取难以直接测量的状态变量的手段在今后的研究中发挥作用，这也是我们后续继续研究的方向。

[1] 荣克林, 张建华, 马道远, 等. CZ-2F火箭POGO问题研究[J]. 载人航天, 2011, 17(4): 8-18. [Rong Kelin, Zhang Jianhua, Ma Daoyuan, et al. Research on POGO problem for CZ-2F rocket[J]. Manned Spaceflight, 2011, 17(4): 8-18.]

[2] Oppenheim B W, Rubin S. Advanced Pogo stability analysis for liquid rockets [J]. Journal of Spacecraft and Rockets, 1993, 30(3): 360-373.

[3] 荣克林, 王帅. 航天装备结构动力学问题总结[J]. 强度与环境, 2016, 43(2):1-8. [Rong Kelin, Wang Shuai. Summary of structural dynamics of space equipment[J]. Structure Environment & Engineering, 2016, 43(2): 1-8.]

[4] 谭述君, 王庆伟, 吴志刚. 临界阻尼比法在POGO振动稳定性分析中的适用性[J]. 宇航学报, 2015, 36(3): 284-291. [Tan Shujun, Wang Qingwei, Wu Zhigang. Applicability of critical damping ratio method on POGO stability analysis [J]. Journal of Astronautics, 2015, 36(3): 284-291.]

[5] 严海. 液体火箭的纵向耦合振动（POGO）研究[D]. 哈尔滨工业大学, 2009.[YAN Hai. Research of POGO vibration in liquid rockets [D]. Harbin Institute of Technology, 2009.]

[6] 赵治华. 液体火箭POGO振动的多体动力学建模及稳定性分析[D]. 清华大学, 2011. [Zhao Zhihua. Multibody dynamic approach of modeling liquid rocket for POGO stability analysis [D]. Tsinghua University, 2011.]

[7] Rubin S, Wagner R G, Payne J G. POGO suppression on space shuttle-early studies[R]. CR-2210, NASA, 1973.

[8] Lehtinen B, Lorenz C F. Space shuttle active-pogo-suppressor control design using linear quadratic regulator techniques[R]. NASA, 1979.

[9] Swanson L, Giel T. Design analysis of the Ares I Pogo accumulator[C].45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference &Exhibit. 2009: 4950.

[10] Ransom D, Doiron H. Experimentally Validated Pogo Accumulator Flow Resistance Model[C].47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. 2011: 5774.

[11] 汤波, 于子文, 张青松. 利用稳定性相图进行的POGO抑制设计[J].强度与环境, 2009, 36(1): 32-38.[Tang Bo, Yu Ziweng, Zhang Qingsong. POGO suppression design by the stability phase diagram [J].Structure &Environment Engineering, 2009, 36(1): 32-38.]

[12] 任辉, 任革学, 荣克林, 等. 液体火箭Pogo振动蓄压器非线性仿真研究[J].强度与环境, 2006(03):1-6.[Ren Hui, Ren Gexue, Rong Kelin, et al. A nonlinear model on the simulation of pogo vibrations in liquid rockets [J]. Structure & Environment Engineering, 2006, (3):1-6.]

[13] 满满, 张婷, 司徒斌, 等. 蓄压器POGO抑制机理的向量表示及阻抗分析法[J]. 导弹与航天运载技术, 2018(4):113-115. [Man Man, Zhang Ting, Si Tubin, et al. Vector representation and impedance analysis method on POGO suppression of accumulator[J]. Missiles and Space Vehicles, 2018(4): 113-115.]

[14] 司徒斌, 高普云. 低温运载火箭POGO抑制系统研究[J]. 低温工程, 2006(2): 58-64.[Si Tubin, Gao Puyun. Research on POGO prevention system of low temperature carrier rocket [J].Cryogenics, 2006(2): 58-64.]

[15] 王庆伟, 王小军, 张青松, 等. 液体火箭POGO振动抑制蓄压器参数优化设计[C]. 中国力学学会.中国力学大会-2017暨庆祝中国力学学会成立60周年大会论文集（A）.中国力学学会, 2017: 1397-1406.

[16] 黄怀德. 蓄压器的作用及其设计和实验[J].国外导弹技术, 1980(9):86-101.[Huang Huaide. The function of accumulator and its design and experiment [J]. Missiles and Space Vehicles, 1980(9): 86-101.]

[17] 王小军, 于子文, 张兵, 等. 国内外运载火箭POGO抑制技术研究进展[J]. 中国科学:技术科学, 2014, 44(5): 492-503.[Wang Xiaojun, Yu Ziwen, Zhang Bing, et al. Research progress of POGO suppression technology of carrier rocket at home and abroad [J]. Scientia Sinica (Technologica), 2014, 44(5):492-503.]

[18] Lock M H, Rubin S. Passive suppression of POGO on the space shuttle[R].CR-132452, NASA, 1974.

[19] 张智, 容易, 秦曈, 等. 重型运载火箭总体技术研究[J]. 载人航天,2017, 23(01):1-7. [Zhang Zhi, Rong Yi, Qin Tong, et al. Research on overall technology of heavy launch vehicle[J].Manned Spaceflight, 2017, 23(1): 1-7.]

[20] 胡久辉, 唐一华, 张青松, 等. 基于振动加速度反馈的POGO主动抑制方法研究[J]. 强度与环境, 2016, 43(5): 7-16.[Hu Jiuhui, Tang Yihua, Zhang Qingsong, et al. Investigation of active POGO suppression based on vibration-acceleration feedback[J]. Environment Engineering, 2016, 43(5): 7-16.]

[21] Lock M H, Rubin S. Active suppression of POGO on the space shuttle[R].CR-134749, NASA, 1974.

[22] 张卫东, 刘锦凡, 余延生, 等. 基于补燃循环低温液氧/煤油火箭的POGO稳定性分析[J]. 上海航天, 2016, 33(S1): 36-42. [Zhang Weidong, Liu Jinfan, Yu Yansheng, et al. Analysis of POGO stability for liquid launch vehicle based on LOX/Kerosene staged combustion cycle engine system [J]. Aerospace Shanghai, 2016, 33(S1): 36-42.]

[23] 谭述君, 陈宇, 王庆伟, 等. POGO回路建模新方法及稳定性分析[C].中国力学大会-2017暨庆祝中国力学学会成立60周年大会论文集（B）, 中国力学学会, 2017: 1671-1683.

Design of LQR Controller for Active POGO Suppression of Launch Vehicle

ZHAO Wang1,2LIU Jin-fan3TAN Shu-jun1,2MAO Yu-ming3WU Zhi-gang1

(1 State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116023, China; 2 Liaoning Key Laboratory of Aerospace Advanced Technology, Dalian University of Technology, Dalian 116023, China; 3 Aerospace System Engineering Shanghai, Shanghai 201109,China）

Aiming at the problem that traditional accumulators cannot meet the requirements for Pogo suppression of large strap-on launch vehicles., an active Pogo suppression method based on LQR controller design is proposed.The active control unit model of Pogo systemic established for a launch vehicle with low temperature liquid oxygen/kerosene refuel cycle engine, by which the state space model of Pogo control system isderived. With the minimum pump inlet pressure as the performance index, the LQR full state feedback controller and partial state feedback controller are designed to realize active Pogo suppression, respectively. Furthermore, the influence of controller size and installation position on the control performance is studied. Finally, the stability analysis and time-domain simulation of the active Pogo suppression design of a certain launch vehicle are implemented. Results show that the proposed active Pogo suppression design has strong robustness and is superior to the traditional accumulator design. And the control performance is not sensitive to the controller size and installation position, which is beneficial to engineering implementation.

POGO vibration; Stability; active Pogo suppression; LQR; robustness

V475.1

A

1006-3919(2021)01-0047-10

10.19447/j.cnki.11-1773/v.2021.01.007

2020-08-15；

2020-09-21

国家自然科学基金面上项目（11972101，11872381），中央高校基本科研业务费（DUT18GF111）

赵旺（1994—），男，博士生，研究方向：航天器动力学与控制；(116023)辽宁省大连理工大学综合1号实验楼409A.