一种基于不确定Petri 网的推理算法

申 鑫，李孝忠

(天津科技大学人工智能学院，天津300457)

Petri 网是一种适合知识表示与推理的异步并发建模工具，具有严格的数学定义和直观的图形表示[1].传统Petri 网利用其异步并发的特性，可以在确定知识的基础上进行更加有效的精确推理.在实际生活中，通常是在信息不完善、不确定的情况下进行思维、求解问题，因而在不确定环境下讨论知识的表示与推理具有重大的意义.Looney[2]提出了模糊Petri网(FPN)模型，用于基于模糊规则系统的模糊推理.此后，FPN 模型逐渐用于模糊的知识表示与模糊推理中，并得到了广泛和深入的研究与应用.Chen等[3]提出了一个更通用的模糊Petri 网模型模拟知识并描述了一个模糊算法自动执行知识推理.Yeung等[4]通过引入阈值和权重的知识参数对上述模糊Petri 网模型进行了改进.Chen[5]对文献[3]的工作进行了扩展，主要描述基于知识的系统的模糊后向推理算法，其中模糊Petri 网被用于在专家系统的知识库中表示模糊产生式规则.之后，也有学者对FPN 模型做出了改进，提出了模糊推理Petri 网(FRPN)模型[6]以及一致性模糊Petri 网(CFPN)模型[7]，用于含有否定命题的模糊产生式规则的表示与推理.

因为FPN 模型的图形表示与动态处理能力，使其被广泛应用于解决各种工程问题.为了给拆卸设备结构的计算机辅助进行快速设计提供理论指导，苏开远等[8]提出了一种基于Petri 网构建功–构映射模型的方法，为得到最优的废旧产品拆卸装备的设计方案，引入了模糊数对设计方案进行评价.为了提高电机的维护效率，实现电机实时故障诊断功能，程学珍等[9]提出了一种具有自适应性的神经模糊Petri 网故障诊断方法，该方法能够准确地诊断出三相异步电动机的故障.

FPN 模型在解决具有不确定性的知识表示与推理的问题上取得了极大的进步.但根据Chen 等[3]提出的模糊推理执行规则，FPN 模型在使用此执行规则解决以下类似问题时可能会出现错误结果.假设一辆车通过桥梁的可能性为0.9，该车要连续穿过30座桥梁，当采用FPN 模型进行推理时，得出该车连续通过30 座桥梁的可能性为300.9=0.042，即该车几乎不能连续穿过30 座桥梁，这与主观经验判断该车能够连续通过30 座桥梁相矛盾.因此，当使用FPN 模型进行推理时，会使一个能够发生的命题被判断成不会发生，导致出现与主观判断相反的结果.

Liu[10]提出了具有规范性、单调性、自对偶性、可列次可加性和乘积测度公理的不确定理论，用于刻画主观不确定性.不确定理论可以代替模糊数学处理问题，而且在刻画主观不确定现象时，不会产生上述的矛盾和悖论，因此得到了广泛的认可和应用.本文结合Petri 网与不确定理论，提出了不确定Petri 网模型(Uncerainty Petri Net，UPN)，用于不确定产生式系统的表示与推理，能够有效避免把可以发生的命题判断成不会发生，产生与主观判断相矛盾的结果.

1 预备知识

假设Г 是一个非空集合，L 为Г 上的σ–代数.每个元素Λ∈L 都称为事件，对每个事件Λ 都分配一个数值 M { }Λ ，用于表示人们相信事件Λ 发生的信度.并且，信度不是随机分配的，其必须具有某些数学属性，为了合理处理信度，不确定测度M 应满足Liu[10]提出的如下3 条公理.

公理1(规范性)对于全集Γ，有 M ( Γ) =1.

公理2(自对偶性)对于任何事件Λ，都有

公理3(次可加性)对于任意可数的事件列Λ1,Λ2,…,Λi都有

定理1[11](Chen-Ralescu)假设X1, X2,…,Xn是独立的不确定命题，并且分别具有真值 α1,α2,… ,αn，则对于Boolean 函数f，不确定命题Z =f ( X1, X2,…, Xn)具有真值

其中ix 取值为0 或1，iv 的定义为

不确定假言推理[12]：设A 和B 是独立不确定命题.假设A 和A→B 分别具有真值a 和b.A 和B 的真值分别用符号1α 和2α 表示.

由不确定蕴含模型[12]式(3)可知，不确定假言推理的蕴含模型可以表示为式(4).

2 不确定产生式规则及其Petri网表示

知识是客观世界中事物之间关系的反映，具有相对正确性、不确定性、可表示性和可利用性[13].产生式表示法用于描述事物之间存在因果关系的知识，描述一个事件的存在而导致另一个事件的产生.用符号方法表示为IF A THEN B（ 或A→B） .其中，A 表示前提命题，B 表示结论命题.

2.1 不确定产生式规则

不确定产生式规则用于表述真实世界中不确定事件之间的因果关系.

不确定事件可以看成一个不确定命题，不确定命题是一个句子，其真值是用不确定测度量化的[10].真值是不确定命题为真的不确定测度.不确定命题的真值可以用定理1 进行计算.

设R ={R1, R2,…,Rn}是一个不确定产生式规则的集合，推理规则的表示符号为Ri:Xj→Xk(CF = ci).其中，Xj和 Xk表示含有不确定变量的不确定命题，并且具有范围为从0 到1 的真值，其真值越大表示该命题越可能为真.ic 表示规则iR 的信度，其范围为从0到1，其信度越大表示该规则越被人们相信.

由Looney 等[14]所述，结合不确定理论可以得出不确定产生式规则在推理中可以分为如下4 种类型.

其中：αi表示规则 Ri中命题Xi的真值，ci表示规则Ri的信度.

类型四的规则由于没有具体含义，所以并不适合推理演绎.因此，本文不考虑类型四的规则.

2.2 不确定产生式规则的Petri网表示

Petri 网是知识表示中常用的一种方式，因此可以利用Petri 网结构表示不确定产生式规则的3 种类型.其中，命题相当于Petri 网中的库所，在图中用圆圈表示，每个库所可以包含托肯或不包含托肯，在图中用点表示此库所有托肯，托肯值的范围为从0 到1，表示命题的真值，其取值越大则该命题越真.规则相当于Petri 网中的变迁，在图中用竖线表示，规则信度的取值范围为从0 到1，表示对此规则相信的程度，其取值越大则该规则越被相信.规则的推理过程可以用Petri 网的变迁触发表示.变迁触发后输入命题的托肯不会被移除，这是因为规则的执行仅仅是命题真值的传播，命题真值不会因为变迁被触发而消失，命题真值大小仅代表该命题被相信的程度.命题之间的因果关系可以用Petri 网中的库所和变迁之间的弧类比表示.

根据以上规则，不确定产生式规则的3 种类型用Petri 网结构表示如图1—图3 所示.

图1 类型一的Petri网表示Fig. 1 Petri net representation of type one

图2 类型二的Petri网表示Fig. 2 Petri net representation of type two

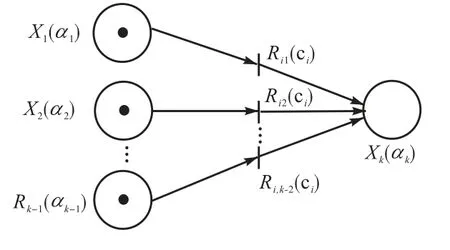
图3 类型三的Petri网表示Fig. 3 Petri net representation of type three

类型三规则在用Petri 网表示前需要先转化成规范式，为

3 不确定Petri网

3.1 不确定Petri网的定义

不确定Petri 网是在定义1 的基础上，结合不确定理论，对传统Petri 网进行了扩展，用于不确定知识的表示与推理，其定义如下.

c 是一个关联函数，表示从变迁到实数的映射，得到规则 Ri的信度，其范围是从0 到1；其信度大小是由专家根据不确定测度给出的数值.

α 是一个关联函数，表示从库所到实数的映射，得到命题Xi的真值，其范围是从0 到1.其真值大小是命题为真时的不确定测度.

β 是一个关联函数，表示库所与命题之间双向映射.

3.2 UPN的执行规则

与传统的Petri 网类似，UPN 的执行规则包括变迁是否具有发生权以及是否能被触发.

如果规则 ri∈ R是能够发生的，当且仅当Xi(Xi是ri的输入命题)是被标记的，即其具有托肯.

根据式(5)可知，对于能够发生的规则ri，当输入命题的真值与规则的真值之和小于1 时，其没有可行解，真值无法被分配，即该规则ri无法被触发，所以要得到触发，则必须满足 T ( Xi)+T ( ri) ≥ 1.

采用FPN 模型进行推理时，其执行规则借助模糊理论中的模糊推理，根据前文提出一辆车连续穿过30 座桥梁的例子可知，使用该规则进行推理可能会使一个能够发生的命题被判断成不会发生.

本文借助不确定理论中的不确定假言推理执行推理规则，对不确定产生式规则的3 种类型进行推理，从而得到所需命题的真值.

4 不确定推理

不确定推理是通过不确定集理论从人类知识中得出结果的过程，需要做到从已知的不确定命题的真值中，通过变迁的触发，得到其他命题的真值，从而建立不确定Petri 网的动态推理模型.基于UPN 的推理算法如下：

(1)判断变迁 ti是否具有发生权，若有则转到第二步，否则继续寻找下一变迁进行判断，直到无变迁能够发生，则推理结束.

(2)根据Chen-Ralescu 定理，得到具有发生权的变迁 ti的输入命题Xi的真值θ.

(3)判断变迁 ti的信度 ci与输入命题Xi的真值θ的和是否大于等于1，若是则该变迁能被触发，进行第四步，否则转到第一步，寻找下一个具有发生权的变迁.

(4)根据不确定假言推理的蕴含模型进行计算，由式(5)得到该变迁的输出命题的真值，如果该命题由多个变迁触发，则根据最大不确定原则，选择最接近0.5 的值为该命题的真值.

(5)回到第一步，寻找下一个具有发生权的变迁，继续计算新的命题真值，直到没有新的具有发生权的变迁，推理结束.

5 案例分析

以燃气轮机故障诊断推理系统为例[15]阐述不确定Petri 网模型，进行基于UPN 的推理，最终得到燃气轮机各个部位发生故障的信度，以便相关人员制定检测维修策略，保障燃气轮机正常工作.设X1表示机组功率过低，X2表示机组耗油量过高，X3表示涡轮前燃气温度过高，X4表示涡轮效率过低，X5表示压气机叶片断裂，X6表示压气机气流通道零件磨损，X7表示涡轮叶片磨损，X8表示压气机喘振.根据燃气轮机经常出现故障的因果关系，可得以下不确定产生式规则为

并且已知命题X1的真值为1.0，命题X2的真值为0.20，命题X3的真值为0.30，命题X4的真值为0.80，由此根据基于UPN 的推理算法得出其他命题的真值.

(1)命题X1—X9用库所(圆圈)表示，规则R1—R4用变迁(竖线)表示，命题之间的因果关系用库所和变迁之间的弧表示，用库所(圆圈)中的点表示命题X1—X4具有真值.则案例的不确定产生式规则可以由图4 所示的不确定Petri 网表示.

图4 不确定产生式规则的UPN表示Fig. 4 UPN representation of uncertain production rules

(2)根据基于UPN 的推理算法，推理过程如下：

f. 再继续寻找下一个具有发生权的规则，命题X6由变迁 t1触发，获得托肯值，所以规则R4具有了发生权，根据触发规则，得出变迁 t4的信度与其输入命题真值的和大于1，所以规则R4可以被触发，经计算得T ( X8) =0.90.由于命题X5不具有托肯，所以规则R3不具有发生权，推理结束.

据此得出出现压气机气流通道零件磨损的故障信度为0.50，出现涡轮叶片磨损的故障信度为0.80，出现压气机喘振的故障信度为0.90.本案例用模糊Petri 网进行推理，得出的结论是出现压气机气流通道零件磨损的故障可能性为0.16，出现涡轮叶片磨损的故障可能性为0.64，出现压气机喘振的故障可能性为0.144.其数据对比见表1.

表1 不确定推理与模糊推理的结果数据对比Tab. 1 Comparison of the result data of uncertain reasoning and fuzzy reasoning

实际上，根据专家经验，如果燃气轮机的机组功率很低且涡轮效率也很低，那么涡轮叶片会出现很大程度的磨损.如果机组功率特别低，而其耗油量不太高以及涡轮前燃气温度微高，则压气机气流通道零件会出现一定程度的磨损.如果压气机气流通道零件出现磨损，那么压气机会有很大可能出现喘振故障.与模糊推理得出的可能性数据相比，本文的不确定推理得出的信度更符合实际情况.

6 结 语

(1)基于不确定理论提出不确定产生式规则，该产生式规则的前提和结论都是不确定命题，规则本身也有信度.

(2)结合不确定理论与Petri 网，提出不确定Petri网模型，对传统Petri 网中的元组进行扩充、对变迁引发规则进行重新定义，提出不确定Petri 网的定义，用于表示不确定产生式系统.

(3)提出不确定推理算法，把不确定产生式规则转换成UPN 表示，通过UPN 的执行规则进行不确定推理，用于解决具有不确定性的知识表示与推理.

(4)将不确定推理算法应用到燃气轮机故障诊断推理系统中，得出该算法可以并行、有效地执行推理过程，得到所求命题的真值，并且有效地弥补了使用模糊Petri 网解决此类问题中出现的不足.