考虑局部屈曲的H 形截面钢构件单轴压弯恢复力模型研究

陈乐川，程 欣，陈以一

(1. 太原理工大学土木工程学院，山西 030024；2. 同济大学土木工程防灾国家重点实验室，上海 200092)

本文将宽厚比较大的板件，即不满足截面分类准则中塑性截面(S1 级截面)要求的板件，称为薄柔钢截面。如果限定相同的单位长度重量，则薄柔截面钢构件相对塑性截面钢构件具有更大的抗弯刚度、屈服弯矩以及弹性整体稳定性，经济性能指标较高，可大量用于轻量化低多层钢框架体系中[1]。陈以一等[2-6]对薄柔截面钢构件压弯作用下的抗震性能研究显示薄柔截面钢构件的塑性性能是可以考虑应用在结构设计中的。然而由于板件宽厚比较大，局部屈曲的提前发生阻碍了塑性铰的形成，被我国抗震规范排除在外，认为抗震设防区不适宜使用这类结构[7]。为贯彻国家提出的“鼓励用钢，合理用钢”的经济政策，我国钢结构抗震设计的一个重要发展趋势是从采用单一化的高延性结构转向针对不同延性等级的性能化抗震设计，以减少结构的用钢量[8]。基于性能化抗震设计的理念，将薄柔钢构件应用于抗震结构中是十分经济可行的。而提出该类构件的恢复力模型是将其推广应用于抗震设计的重要基础。

Kato[9-10]基于简化的双翼缘模型和简化的材料本构关系得到了较厚实截面的弯矩-曲率关系。Wu 等[11]提出了一种混合仿真模型计算方法，并通过一个足尺框架模型验证了该计算方法下所提出的截面本构模型的有效性。王萌等[12-14]采用了不同的模型研究了强震作用下结构发生局部屈曲造成损伤对钢框架结构抗震性能产生的影响，提出了能够考虑累积损伤、刚度和强度退化的钢材等效本构模型。Kumar 和Usami[15]对薄壁焊接箱形截面钢构件的滞回性能进行了研究并提出了考虑局部屈曲累积损伤的构件恢复力模型。赵静[16]提出了可以较好的考虑薄柔板件局部屈曲的弹塑性轴向弹簧层次恢复力模型。上述研究结果表明，目前已有学者从多个层次对薄柔截面钢构件恢复力模型展开了研究，但对考虑局部屈曲的截面层次恢复力模型的研究还较为有限，且集中在绕强轴压弯的恢复力模型，对绕弱轴的情况研究较少。截面层次的恢复力模型适用于不同构件长度、受力状态、边界条件等，具有广泛的适用性，因此有必要对薄柔构件截面层次的恢复力模型展开研究。

本文通过对不同宽厚比及轴压力组配下的H 形截面钢构件进行参数分析，建立了单轴压弯作用下考虑局部屈曲破坏的H 形截面恢复力模型，准确地描述H 形截面各项性能的退化情况，为研究不同边界条件和受荷方式下H 形截面的刚度变化及滞回性能提供理论依据。

1 有限元模型的建立与校核

1.1 已有试验研究

Chen 等[17]和Cheng 等[18-19]分别对不同宽厚比和轴压比组配下的薄柔H 形截面钢构件进行了绕强轴和弱轴压弯的循环加载试验，试件板件宽厚比组配如图1 所示。Cheng 等[17-18]采用在常轴压力和分别沿两主轴方向的循环水平荷载作用下的悬臂构件作为基本加载模式，如图2(a)和图2(b)所示。其试验装置如图2(c)所示，试件平躺于反力框架中，轴向千斤顶提供恒定的轴向力，通过控制200 kN 伺服作动器实现柱顶的往复水平加载，侧向支撑保证对试件另一方向的位移约束。在千斤顶和伺服作动器的底部分别设有跟动装置，保证试件在发生大位移后仍然可以实现轴力和水平荷载的方向不变。千斤顶和伺服作动器在柱顶处采用万向球铰与试件相连，以释放柱顶转动约束。

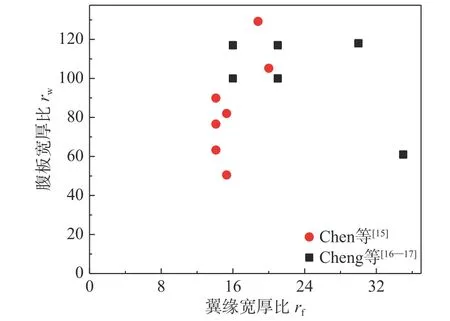
图 1 试件组配情况Fig.1 Width-to-thickness ratio of test specimens

图 2 加载条件与试验装置Fig.2 Loading condition and test setup

基于局部屈曲的发展与构件塑性变形能力的关系，阐释了板件宽厚比、轴压比及加载方向对构件强度、延性以及耗能等滞回特性的影响机理。得到以下重要结论：1)靠近柱底区域的局部屈曲破坏是所有试件的主要破坏模式；2)局部屈曲的发生将导致截面达到最大抗弯承载力，因此将滞回曲线划分为非退化(屈曲前)阶段和退化(屈曲后)阶段；3)翼缘和腹板的宽厚比及轴压比是影响H 形截面压弯作用下各阶段滞回性能的主要因素；4)在退化阶段，强度、卸载-重加载刚度均会受到局部屈曲引起的累计损伤影响而退化，且各项滞回特性均受到板件屈曲相关作用的影响；5)绕弱轴压弯时不同的腹板屈曲模式导致了不同的滞回响应，其中当翼缘宽厚比较大、腹板宽厚比较小且轴压比较小时，翼缘屈曲而腹板不发生屈曲，此时恢复力曲线会在位移较大时出现刚度随着位移增大而增大的现象，本文称之为刚度滞升现象。

结合相关试验结果，在本文模型研究中着重考虑以下几点：1)考虑各项参数相关作用的影响；2)着重关注截面在退化阶段的各项性能；3)对于有不同滞回特性的部分应当明确其界限并使用不同的模型。

rf和rw分别为考虑屈服强度影响的翼缘和腹板的宽厚比，n 为轴压比。主要参数定义为：

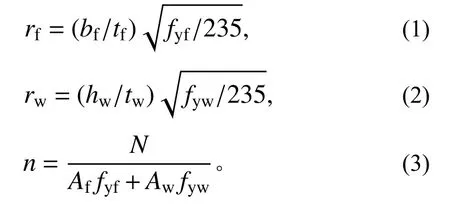
式中：fyf和fyw分别为翼缘和腹板的屈服应力；bf和tf分别为翼缘的宽度和厚度；hw和tw分别为腹板的宽度和厚度；Af和Aw分别为翼缘和腹板的面积；N 为轴压力。如图3 所示。

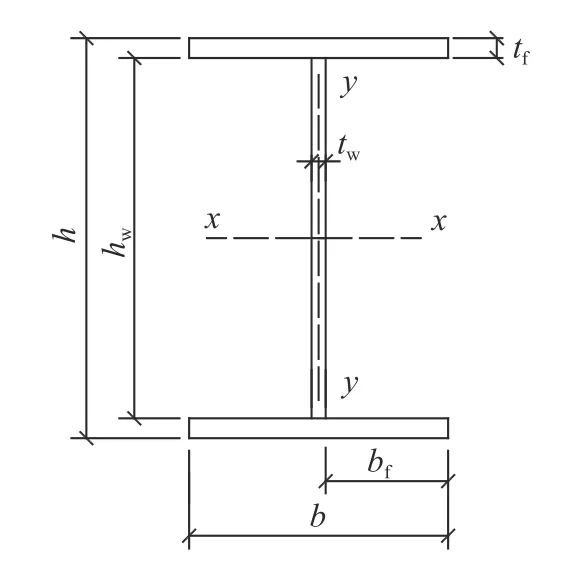
图 3 H 形截面定义Fig.3 Definition of H-section

1.2 ABAQUS 有限元模型的建立

为了确定恢复力模型的各项参数，现有的试验结果远远不够。因此，本文通过ABAQUS 有限元软件建立H 形截面钢构件分别绕强轴和弱轴压弯的非线性有限元模型。

本文在Cheng 和Chen[20]建立有限元模型的方法的基础上，将单调加载扩展为循环加载。网格划分和边界条件如图4 所示。Cheng 和Chen[20]利用已有的试验结果对有限元模型进行了校核，有限元模型可以模拟试件的极限抗弯承载力、累积耗能以及各项退化性能。校核结果显示所建模型与试验相比基本准确，可以用于本文对恢复力模型研究的参数分析中。

图 4 网格划分和边界条件Fig.4 Mesh generation and boundary condition

1.3 参数分析

参数分析时，钢材采用三折线模型，如图5所示，其中屈服强度fy=345 MPa，极限强度fu=500 MPa，弹性模量E=2.06×105MPa，强化段应变硬化率取Eh/E=0.01，采用随动强化准则。加载时，对构件施加恒定的轴向荷载，然后分别沿强轴和弱轴施加包括每级一圈和每级三圈的水平往复荷载，直至完全破坏，加载制度如图6 所示。

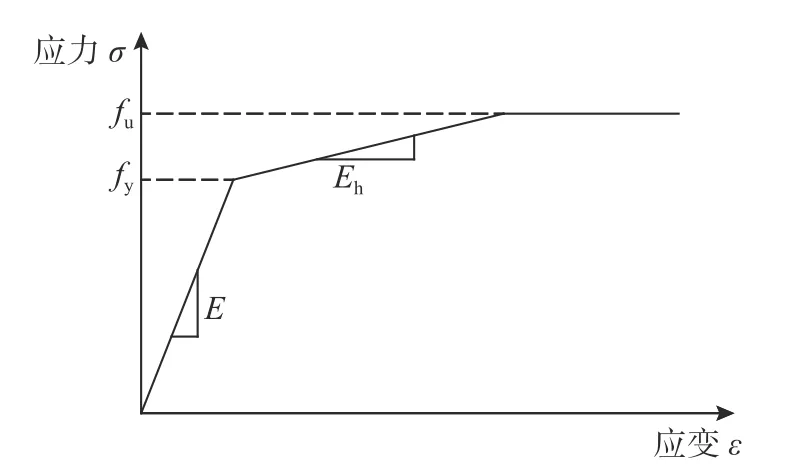
图 5 参数分析材料模型Fig.5 Material model for parametric analysis

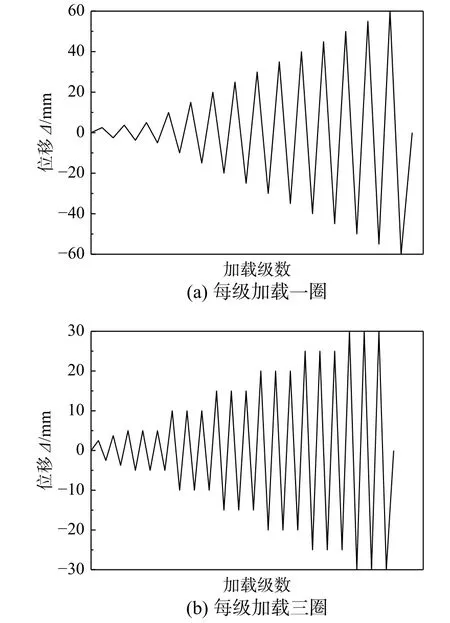
图 6 加载制度Fig.6 Loading protocol

参数分析时采用截面等高(h=300 mm+tf)、等宽(b=200 mm)和构件等长(L=1500 mm)的H 形截面悬臂构件。通过改变板的厚度(tf和tw)和轴向力N 来实现主要参数rf、rw和n 的变化，绕两主轴方向的压弯均采用相同的参数，通过建模时不同的加载方向区分。

关键参数列于表1，每个不同参数的试件均按所绕不同主轴和每级循环一圈或三圈，共建立了600 个有限元模型，有限元模型以S(strong axis)/W(weak axis)-n-rw-rf-Ci(i=1,3)的形式命名。以W-0.2-80-25-C1 为例，表示每个加载级绕弱轴循环一圈，n=0.2，rw=80，rf=25 的模型。

1.4 基于铰区模型的截面层次的M-φ 曲线

在试验结果和有限元模拟的结果中，只能得到特定长度及加载条件下构件层次的力-位移曲线。为了将其应用于其他长度、受力状态、边界条件的构件或结构体系中，笔者[21]提出了铰区内截面层次的弯矩-曲率曲线的计算方法。其中铰区弯矩M 为：

表 1 关键参数取值Table 1 Key parameter value

铰区曲率的计算原则如图7 所示，将构件(L)分为弹性区(Les)和铰区段(Lh)，水平位移Δ 由铰区位移Δh和弹性段位移Δes组成。假定铰区范围内曲率相等，那么铰区的平均曲率为：

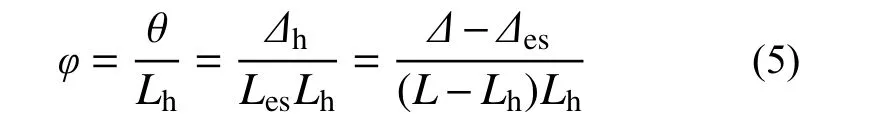
图 7 悬臂构件变形分解图Fig.7 Decomposition of deformation of a cantilever member

绕强轴压弯铰区长度Lh为：

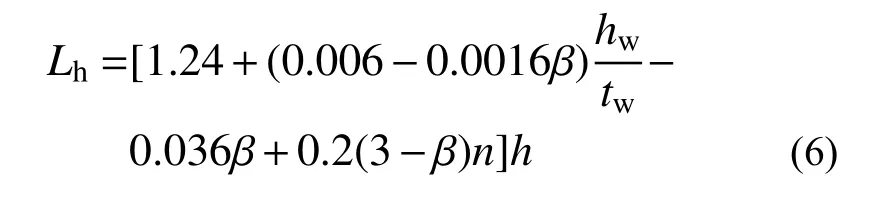
绕弱轴压弯铰区长度Lh为：

2 单轴压弯恢复力模型

恢复力模型主要包含骨架曲线和滞回规则两个方面，骨架曲线是循环加载幅值渐增时滞回曲线峰值的连线，滞回规则是表征卸载-重加载时的非线性性能。本文在参数分析的基础上分别得到了H 形截面绕强轴和绕弱轴压弯的恢复力模型。

2.1 恢复力模型的一般描述

2.1.1 恢复力模型

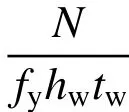
图 8 一般退化模型Fig.8 General degradation model

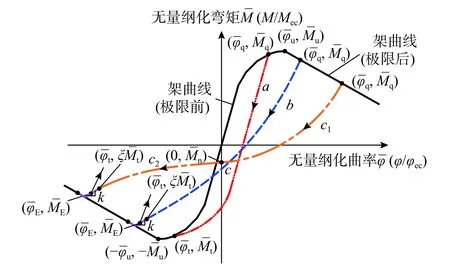
图 9 刚度滞升模型Fig.9 Increased reloading stiffness model

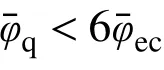
2.1.2 骨架曲线

骨架曲线是滞回曲线的包络线，包含三个阶段：弹性阶段(OA)，此阶段弯矩曲率曲线呈线性关系；强化阶段(AB)，此阶段塑性应力重分布，弯矩增大，刚度减小；极限后阶段(BC)，此阶段由于板件局部屈曲变形的累积，刚度和强度均减小，如图10。

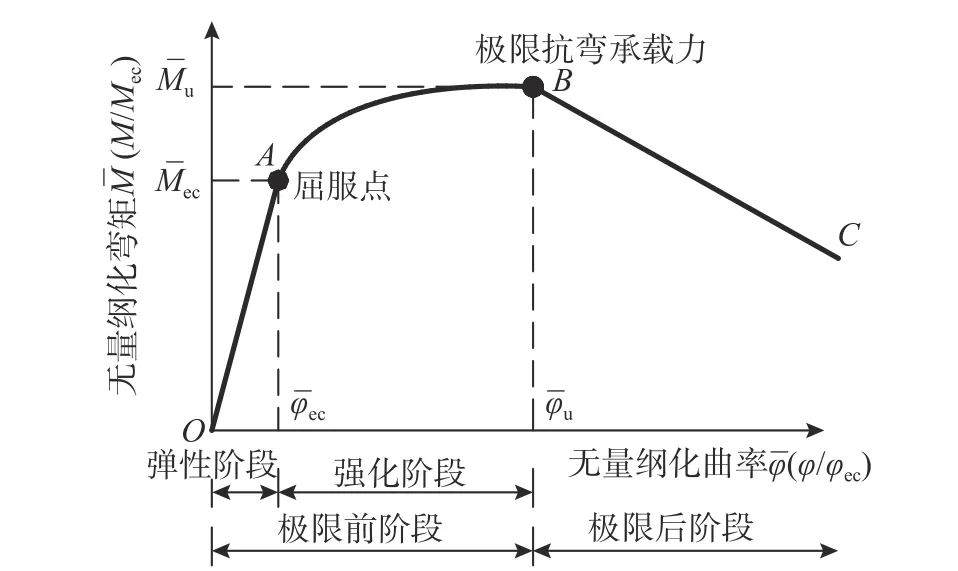
图 10 骨架曲线Fig.10 Backbone curve

骨架曲线由B 点分为非退化阶段和退化段。其中非退化段曲线(OB)采用了Ramberg-Osgood方程[22]，退化曲线(BC)由线性函数描述。根据反对称原理，可以简单推导出反方向的计算公式。

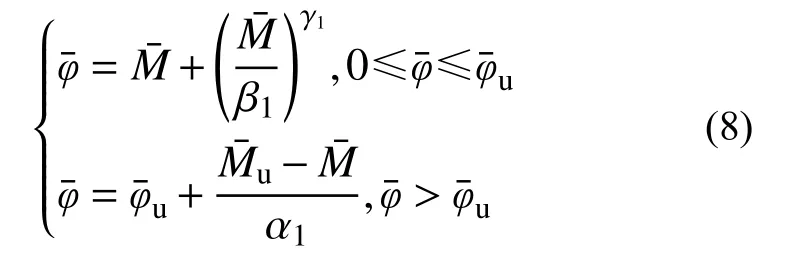
其中，极限曲率为：

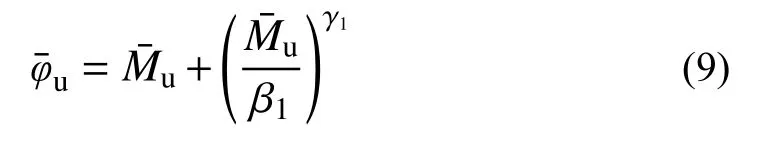
2.1.3 滞回规则

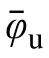
滞回规则的一般描述如下：

1)首次加载沿着骨架曲线进行。

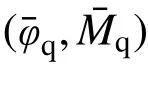
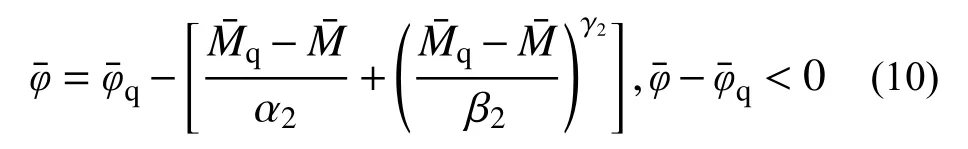
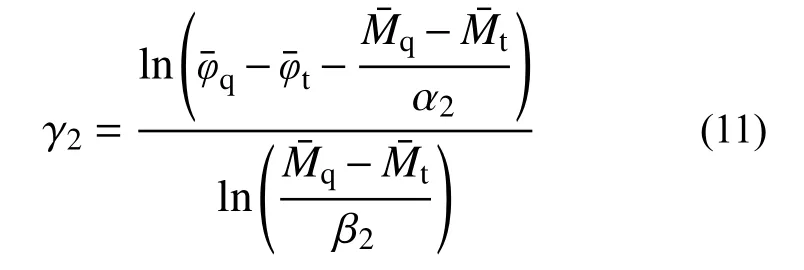
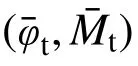
2.2 模型参数的确定

本节利用对H 形截面的试验研究和参数分析的结果，对模型的各项待定参数进行了确定和校核。

2.2.1 骨架曲线

通过参数分析，基于最小二乘法的误差分析原则，确定了骨架曲线表达式(8)的各项待定参数，如下。

绕强轴压弯时：

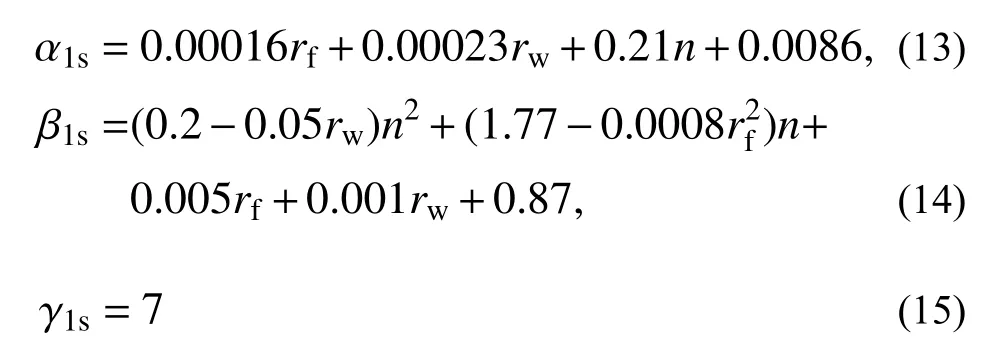
绕弱轴压弯时：

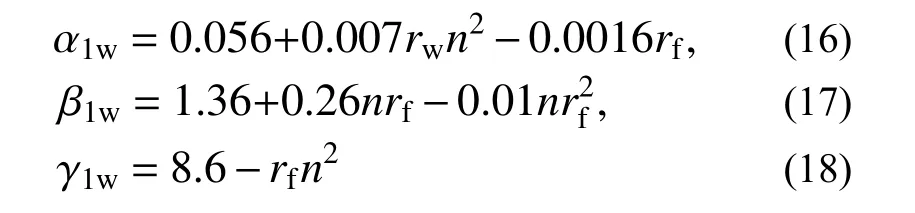
2.2.2 曲线a 的表达式

曲线a 适用于在非退化段卸载及重加载的情况，此时的主要力学行为是无局部屈曲的塑性应力的逐渐扩张。在此阶段，卸载刚度与弹性刚度相同，即α2=1。

曲线a 的表达式(10)进一步改写成：

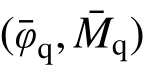
2.2.3 曲线b 的表达式

曲线b 适用于构件绕强轴压弯和无刚度滞升的绕弱轴压弯情况，在退化阶段卸载-重加载的过程。在这一阶段的主要力学行为是由板件局部屈曲带来的损伤累积。滞回环的主要特征量(强度、卸载和重加载刚度)均随着曲率的增大而降低。

根据参数分析，绕强轴和绕弱轴压弯恢复力模型的折减系数的回归表达式分别为：绕强轴压弯时，α2与β2的回归表达式为：

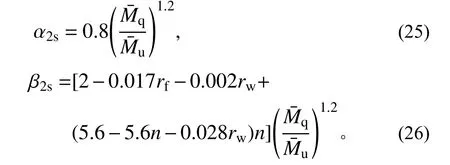
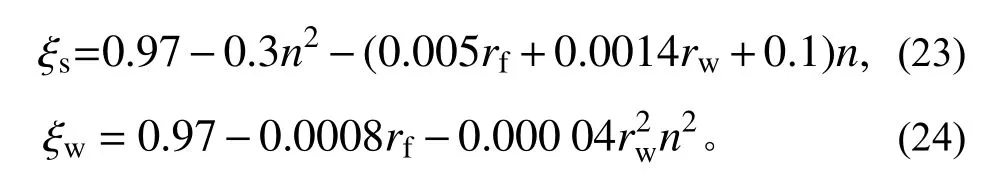
绕弱轴压弯且腹板无屈曲时，α2与β2的回归表达式为：

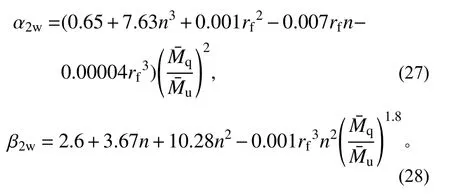
参数γ2可由式(12)求得。

2.2.4 曲线c 的表达式

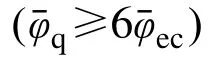
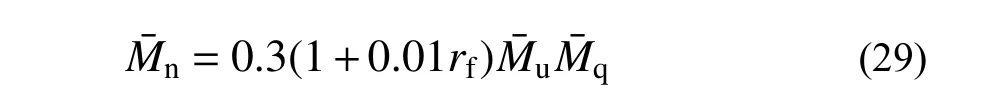
卸载阶段的曲线c1的出发点为(φ¯q, M¯q)，目标点为(0, M¯n)。c1的表达式为：

其中：

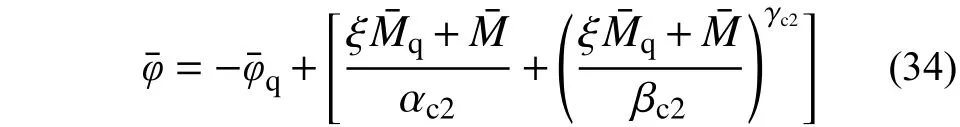
其中：

2.3 恢复力模型的流程图

H 形截面恢复力模型的完整操作流程见图11，根据以下步骤，即可得到给定截面以及加载条件下的全过程恢复力曲线。

第一步：输入截面尺寸信息b、h、tf、tw等；输入截面材料信息fyw、fyf等；输入加载信息：弯矩作用方向、轴压力N、以及加载制度等；通过计算得到截面的特征参数rf、rw、n、Mec、φec等；

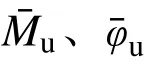
第三步：求得骨架曲线与各滞回规则曲线的参数；

第四步：求得骨架曲线；

第五步：求得滞回规则。

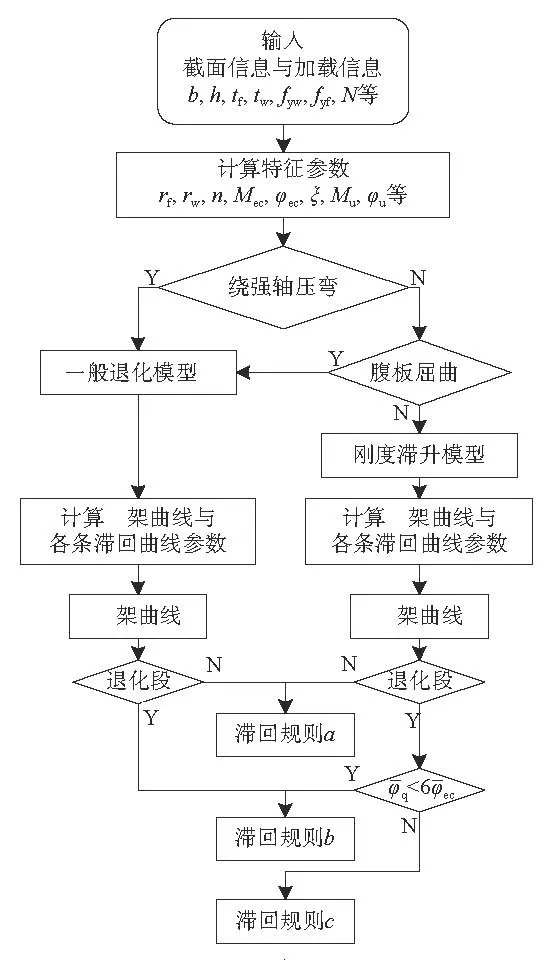
图 11 恢复力模型计算流程图Fig.11 Flow chart of constitutive model calculating

3 模型评价

通过将本文恢复力模型计算结果与试验结果和有限元分析结果的对比，分别验证了所提出的H 形截面绕强轴与弱轴压弯恢复力模型的可靠性。

3.1 滞回曲线的比较

通过该模型预测的弯矩-曲率曲线与Cheng 和Chen[18-19]进行的试验所得的弯矩-曲率曲线进行比较，如图12 所示。并将模型计算所得的弯矩-曲率曲线与H 形截面钢构件绕强轴压弯与弱轴压弯作用下的参数分析结果进行比较，典型模型的比较结果见图13。结果表明，本文所提恢复力模型所得的弯矩-曲率曲线与试验及有限元模型所得的弯矩-曲率曲线具有较好的一致性。

3.2 误差分析

通过与ABAQUS 有限元分析结果的对比，对恢复力模型的极限抗弯承载力、强度、变形和耗能进行了误差分析，进一步验证了滞回模型的正确性。

首先，将有限元分析结果的所有截面模型的极限抗弯承载力Mu,FEA与由PEM 推算的极限抗弯承载力Mu,pred进行比较，如图14 所示。PEM 计算结果与有限元分析结果吻合较好。可见PEM 法对极限抗弯承载力的预测具有较高的准确性。其次，将恢复力模型确定的整个加载过程的耗散能量Et与有限元结果进行比较。用总耗能量的误差来量化模型的整体稳定性，比较结果如图15。表明所提出模型的耗能能力具有较高的准确度。将本文模型与有限元模型计算结果的比值进行统计，统计分析结果列于表2 中，说明了本文模型的整体可靠性。

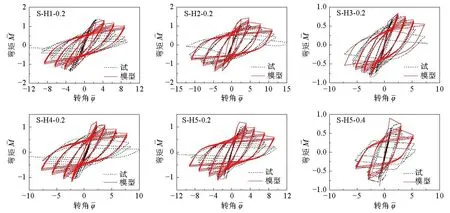
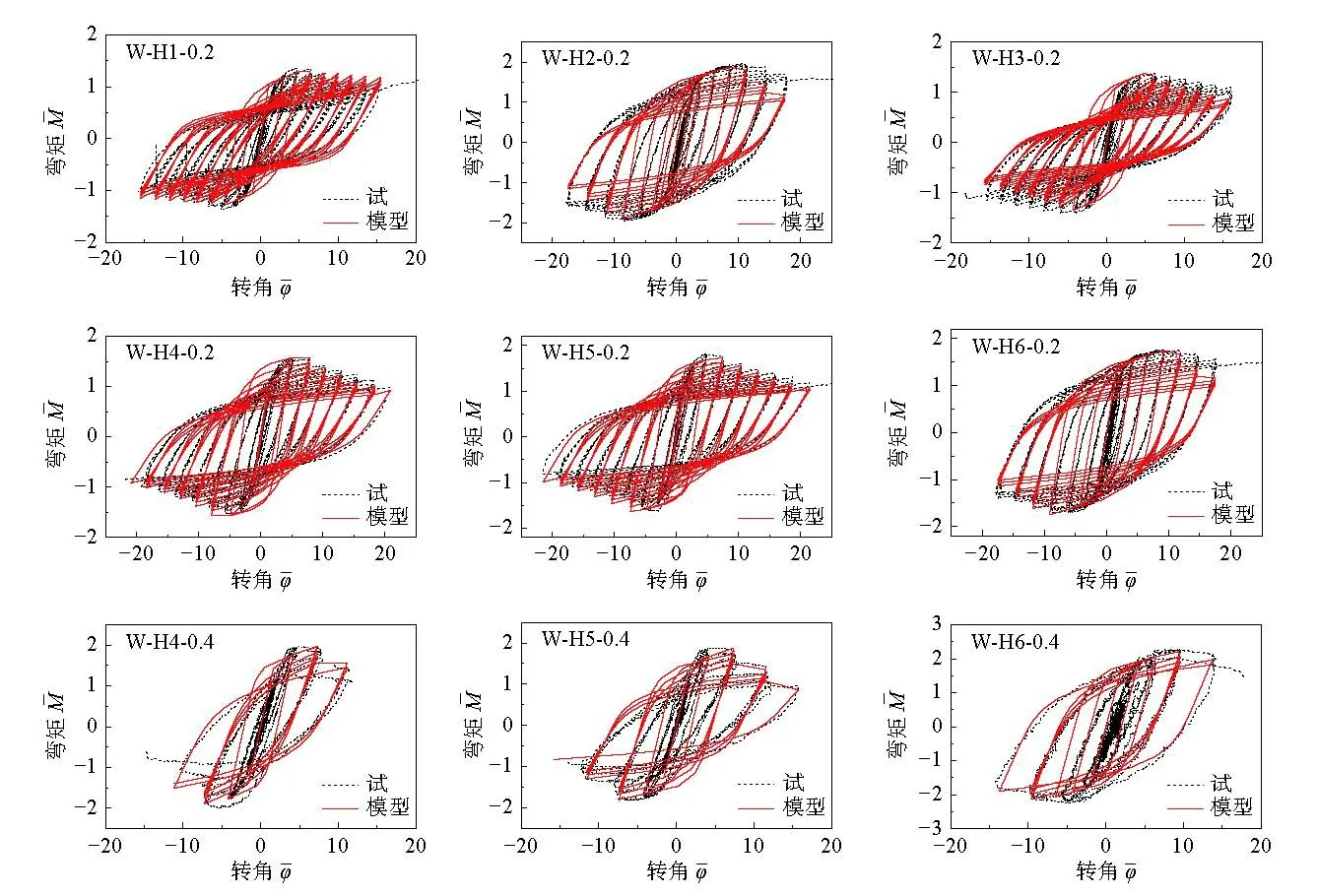
图 12 单轴压弯试验结果与模型滞回曲线的比较Fig.12 Comparison of hysteresis curve between test results and constitutive model

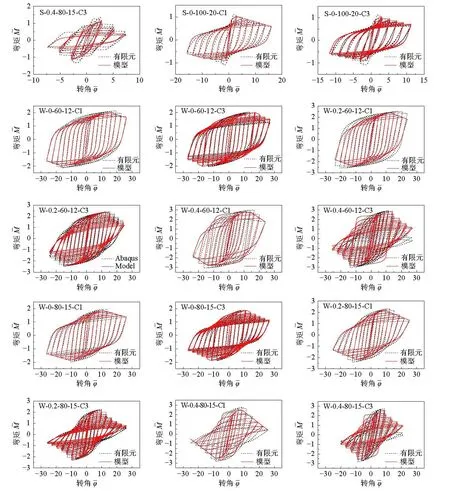
图 13 有限元分析结果与模型滞回曲线的比较Fig.13 Comparison of hysteresis curve between FEA results and constitutive model

3.3 对恢复力模型的评价

以上比较结果从以下几个方面证明了所提出的恢复力模型的有效性：1)能够准确地预测极限抗弯承载力与对应的极限曲率；2)能较好地预测

非退化段的滞回性能；3)通过引入折减系数来考虑局部屈曲引起的累积损伤，可以较准确地反映强度、卸载和重加载刚度的退化；4)能准确区分重加载刚度减小或增大的退化阶段；5)研究了翼缘与腹板宽厚比、轴压比和加载历史对截面非弹性性能的影响。

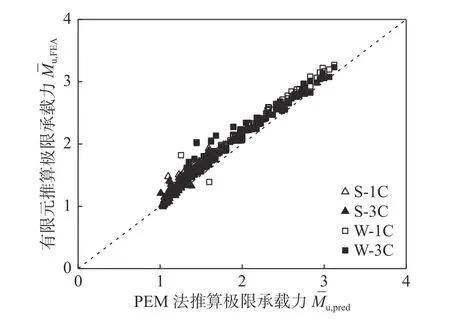
图 14 有限元模型与本文模型的极限抗弯承载力比较Fig.14 Comparison of ultimate strength between FEA results and constitutive model

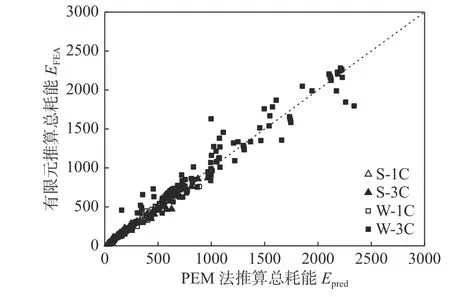
图 15 有限元模型与本文模型的总耗能比较Fig.15 Comparison of total energy dissipation between FEA results and constitutive model

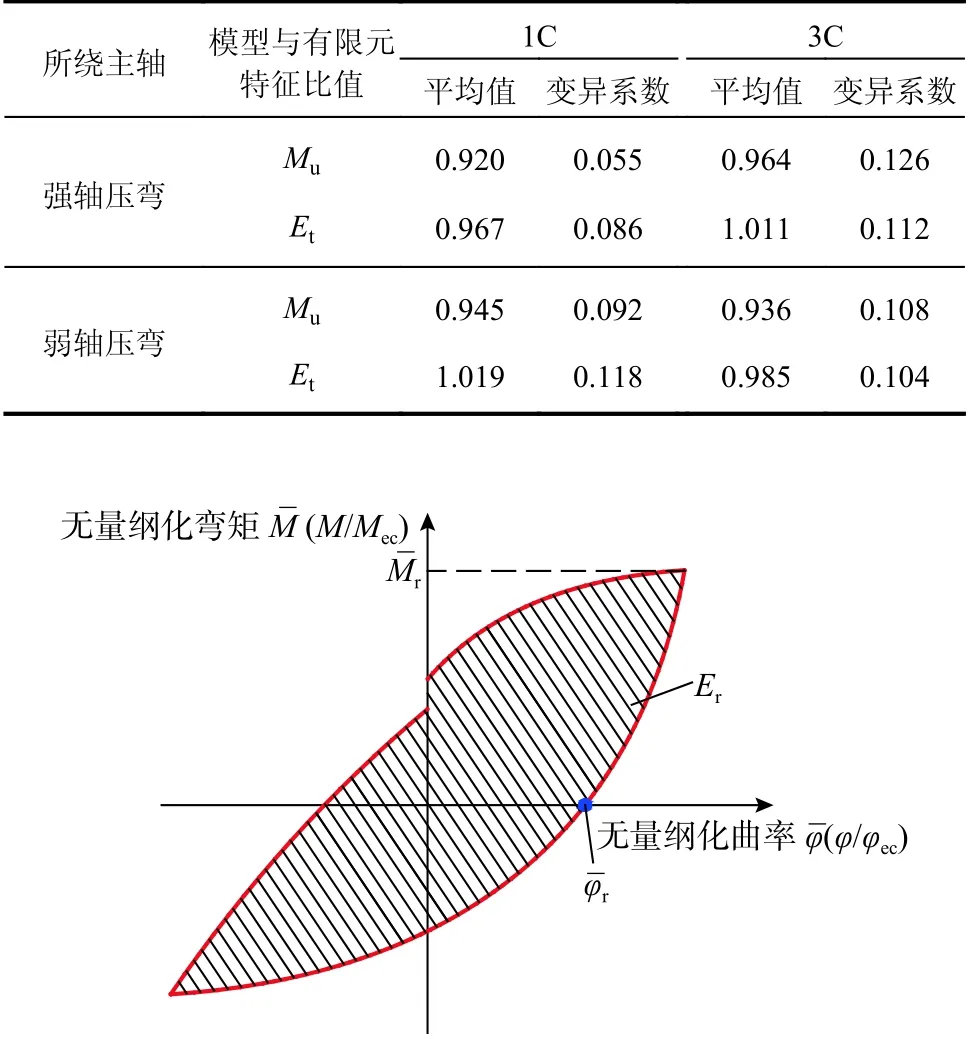
表 2 加载全过程误差分析Table 2 Error analysis in the whole process

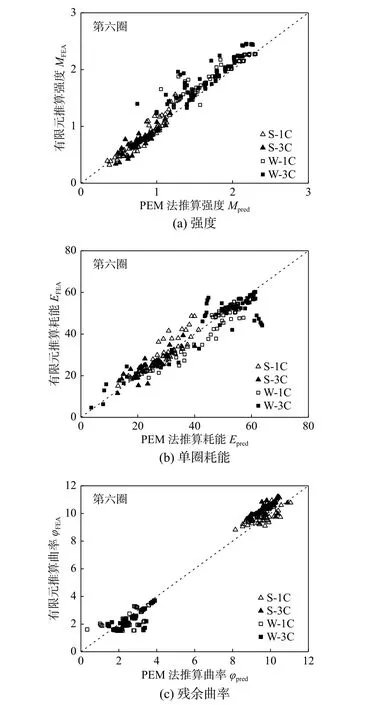
图 17 有限元模型和本文模型的比较Fig.17 Comparison results of 6th loading cycle between FEA results and constitutive model

表 3 第六加载级误差分析Table 3 Error analysis in the 6th cycle

本恢复力模型适用于轴压比为0～0.4，翼缘宽厚比为9～30，腹板宽厚比为45～120，同时受常轴压力和绕强轴或弱轴的单轴弯曲的H 形截面钢构件。

4 结论

本文对不同腹板翼缘宽厚比及轴压比组配下的薄柔H 形截面钢构件进行了参数化分析。提出了一种考虑局部屈曲破坏的截面层次的恢复力模型，通过建立数学表达式来描述薄柔H 形截面钢构件在单轴压弯作用下的弯矩-转角关系，得到了以下结论：

(1)该模型充分考虑了H 型截面绕单轴压弯的滞回特性。基于绕不同的主轴与不同的屈曲模式，提出了多种恢复力模型。恢复力模型包括骨架曲线和滞回规则，这些滞回规则与相应的卸载-重加载路径相匹配。

(2)基于Ramberg-Osgood 方程，采用参数α2、β2、γ2来模拟刚度退化。并用折减系数ξ 来考虑局部屈曲累积损伤引起的强度退化。

(3)确定了在考虑板件相互作用影响下的模型中的所有识别参数。

(4)通过误差分析，该模型能较好地模拟薄柔H 形截面钢构件的非线性行为，所提出的恢复力模型考虑了循环荷载作用下的几乎所有重要影响因素。虽然本模型的适用范围仅限于H 型截面，但基本概念可以扩展到其他类型的薄壁截面。