海上风电大直径单桩的修正p-y 曲线模型

孙毅龙，许成顺，杜修力，杜秀萍，席仁强

(1. 北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124；2. 保定市水利水电勘测设计院，河北，保定 071000)

单桩基础是海上风电常用的基础形式之一，由于海洋荷载环境的复杂性和特殊性，海上风电单桩基础常承受较大的水平荷载，从而导致桩基发生水平位移[1]。基础水平位移过大会影响海上风机的正常运营，因此研究水平荷载作用下海上风电单桩基础的位移反应具有重要意义。

为研究水平荷载作用下桩基的水平变位规律，许多学者开展了大量的研究工作。Reese 等[2]开展了砂土场地下钢管桩的水平加载试验，基于柔性桩模型(长细比为24)试验结果提出了p-y 曲线模型，此方法应用简单且可以较好地反映土体的非线性，因此API、DNV 推荐用p-y 曲线法进行水平受荷桩的承载力设计。近年来，随着海上风电单桩基础桩径的增大，桩基长细比减小，Wiemann[3]通过开展有限元计算发现，对长细比较小的刚性桩，p-y 曲线存在高估初始地基刚度的缺陷；且随着深度的增加，初始地基刚度被高估的更为严重。因此造成海上风电单桩基础设计过于保守，增加建设和运营成本。朱斌等[4]通过开展单桩基础模型试验，再次发现传统p-y 曲线法具有偏大的初始刚度和偏小的极限土抗力。Ashford 等[5]开展桩基水平振动试验，发现初始地基刚度与桩土相对刚度有关，并修正了初始地基模量的计算方法；结果表明，基于Terzaghi 推荐的地基反力模量计算的桩基自振频率与试验实测结果吻合较好。Pender 等[6]开展大量的有限元计算，探究桩基桩径对初始地基刚度的影响，研究结果表明，桩基的桩径影响对地基刚度的影响不可忽略。Abdel-Rahman[7]、Sφrensen 等[8]的研究表明，在极端荷载作用下，p-y 曲线法低估了桩顶水平位移。Kallehave 等[9]对p-y 的初始刚度进行修正，并应用于某风电场计算，结果表明，桩基桩径影响对桩-土间的初始地基刚度影响显著。Sφrensen[10]基于FLAC3D开展了一系列大直径钢管桩的水平荷载数值计算，验证了钢管桩的桩径影响对桩-土初始地基刚度的影响，并发现地基模量与深度之间为非线性关系。朱斌等[11]通过开展大直径单桩水平受荷离心机试验，确认了地基反力模量与深度之间是非线性的。Otsmane 等[12]的研究结果再次表明当前的p-y 曲线中的初始地基刚度存在缺陷。Achmus 等[13-15]结合前人的研究，对当前p-y 曲线的适用性进行了探讨，认为桩径的变化对初始地基模量的影响不可忽略。

实际上，在不同砂土场地，桩径对初始地基模量的影响规律不同，但以往的研究未考虑场地的变异性。本文将开展超密、密实、中密、松散和非常松散五种典型砂土场地下的大直径桩的水平加载数值研究，基于数值计算结果，从土体深度、桩径两方面对初始地基刚度进行修正，在此基础上，对现有的p-y 曲线模型进行修正。最后，通过案例分析对修正的p-y 曲线的正确性进行了验证。

1 现有p-y 曲线模型

海上风电基础承受较大的水平荷载，桩体会发生较大的水平位移，桩周土体将由弹性区进入塑性区。为了模拟桩周土体的弹塑性特性，一般采用API 推荐的p-y 曲线。骨架曲线如图1所示。

式中：P/kN 为土的水平土抗力；y/m 为桩的水平变位；A=(3.0-0.8H/D)≥0.9；k/(kN·m-3)为初始地基模量；H/m 为深度；Put/(kN·m-1)为深度H 处的极限承载力(浅层土下Pus=(C1D+ C2D)γH，深层土下Put=C3DγH，其中C1、C2、C3为随内摩擦角变化的系数，D/m 为桩径，γ/(kN/m3)为土体的有效重度。

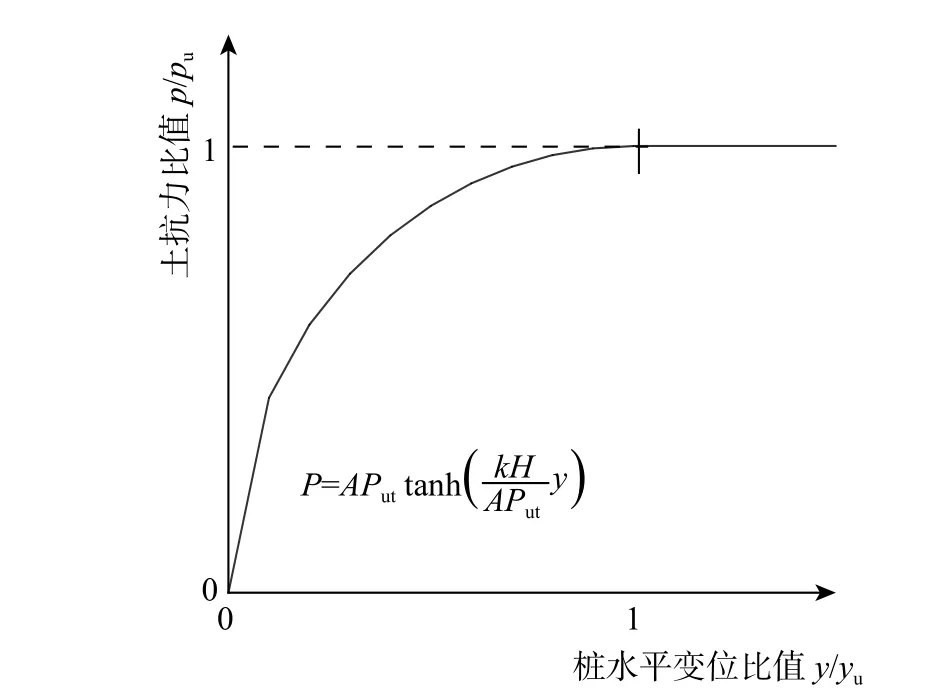
图 1 砂土的p-y 曲线[16]Fig.1 p-y curves for sand[16]

现有p-y 曲线模型的初始地基刚度为：

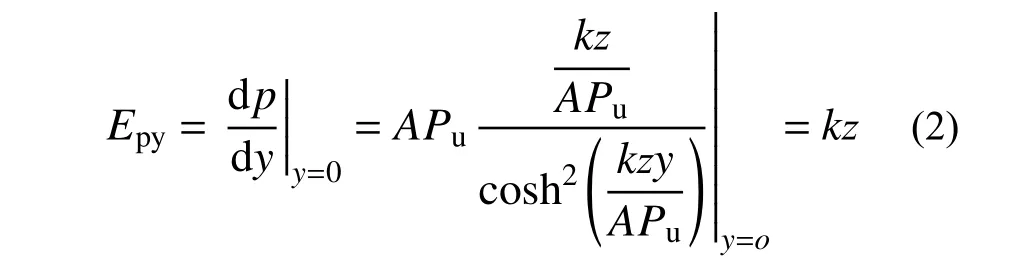
式中，初始地基反力模量常数k 是由砂土的内摩擦角、相对密实度决定的，如图2 所示。

2 修正p-y 曲线模型的初始地基模量

图 2 地基模量常数k 与相对密实度的函数关系(API)[16]Fig.2 Constant of subgrade reaction k versus relative density (API)[16]

许多桩基模型试验证明了在刚性桩的水平位移计算中，API 规范中的p-y 曲线模型存在诸多缺陷[17]。许多学者针对p-y 曲线模型开展了大量研究，经过对比分析，发现现有p-y 曲线模型高估初始地基模量是计算结果不准确的主要因素，所以对现有p-y 曲线模型的初始地基模量进行修正。已有学者的研究考虑的场地条件较为单一，导致确定的修正参数较为绝对化，如表1 所示。因此本节详细探讨了桩径、土体深度、土体弹性模量对p-y 曲线的初始地基模量的影响机理，并建立初始地基模量的修正公式。

2.1 桩径对初始地基模量的影响

桩径的变化引起土体应变水平的变化[18]，如图3 所示。依据弹性理论，Terzaghi[19]发现初始地基模量与桩径、土体弹性模量有关，并建立了初始地基模量的计算公式：

式中：Es/kPa 为土体弹性模量；d/m 为桩径；k/(MN/m3)为地基模量常数，表2 为Terzaghi 推荐的砂土的地基反力模量值。

表 1 已有的p-y 曲线初始刚度修正理论17Table 1 Previously proposed modified methods for initial stiffness of p-y curve17

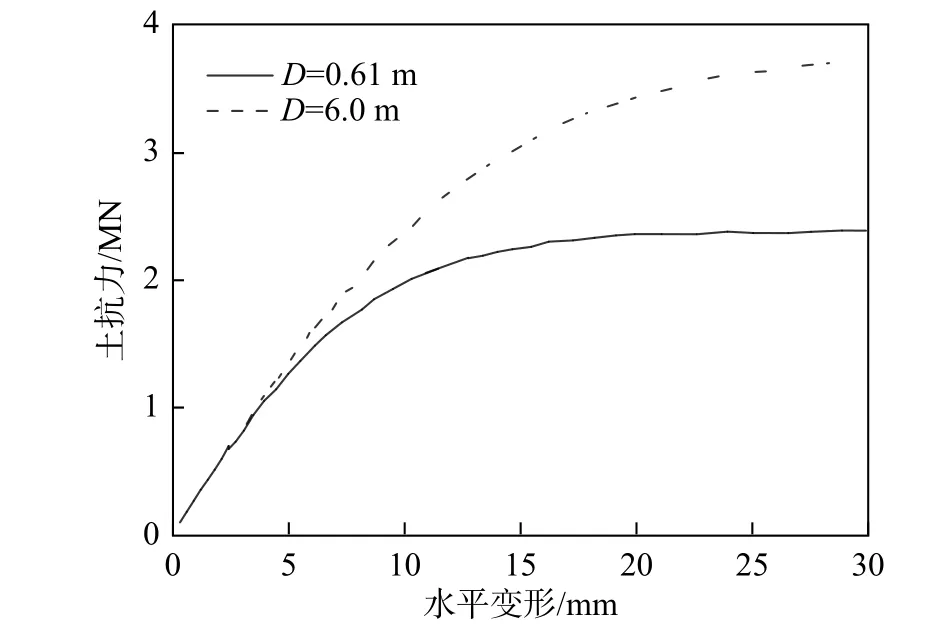
图 3 砂土中深度8 米处的桩的p-y 曲线：(虚线)桩径6 m 和(实线)桩径0.61 m[18]Fig.3 p-y curves at 8 m depth of plies in sand: (dashed line)D=6 m and (solid line) D=0.61 m[18]

由式(3)可知，桩径的变化会影响初始地基模量，杨敏等[20]、Negro 等[21]的研究表明，随着桩径的增大，桩径对初始地基模量的影响增大，即桩径D>2 m 时，桩基的桩径对初始地基模量影响显著。本文基于Stevens 等[22]的研究，结合大直径桩桩径对桩端阻力、桩侧摩阻力的影响规律[23]，确定桩径对初始地基模量的影响表达式为：

表 2 地基反力模量常数k 值[19]Table 2 Constant of modulus of subgrade reaction k[19]

式中：D0为相对桩径，取1 m；m 为桩径影响指数。

2.2 深度对初始地基模量的影响

砂土的弹性模量与土的相对密实度和上覆土的压力密切相关，许多学者通过室内试验验证了弹性模量与砂土密实度和小主应力的函数关系，具体如下[24]：

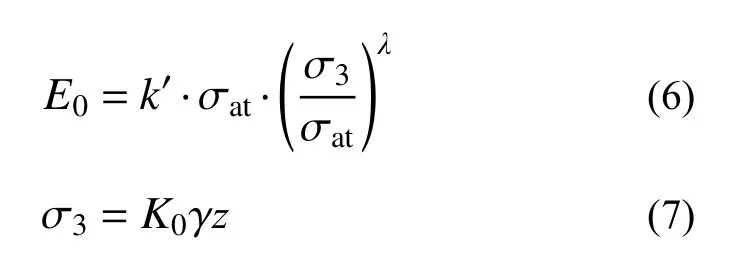
结合式(6)、式(7)得：

式中： E0/kPa 为土体的初始弹性模量；k′与λ、n 由土体的土体密实程度决定； σ3/kPa 为土体的小主应力；K0为土体的静止土压力系数； σat/kPa为参照应力取大气压力；z/m 为土体深度；z0为相对深度，取2.5 m[9]。

2.3 建立初始地基刚度的修正公式

综合桩的桩径、土体深度对p-y 曲线模型的初始地基模量的影响，本文在Kallehave 等[9]提出的修正方法的基础上对现有p-y 曲线模型的初始地基模量进行修正，见式(9)。桩的桩径影响指数和深度影响指数的取值与砂土的密实度和内摩擦角密切相关，本文将在3.2 对m、n 的取值进行分析和定义。

3 确定地基模量修正公式中的参数

基于FLAC3D有限差分计算平台，开展大直径钢管桩的水平承载特性分析。根据计算结果，确定初始地基模量修正公式中的参数m、n。

3.1 数值模型的建立与验证

为验证FLAC3D数值计算模型的有效性和准确性，将数值计算结果与Li 等[25]开展的钢管桩的水平加载模型试验的实测数据进行对比。

3.1.1 FLAC3D数值模型的建立

表 3 Li 模型试验钢管桩参数Table 3 Parameters for pile of Li experiment[27]

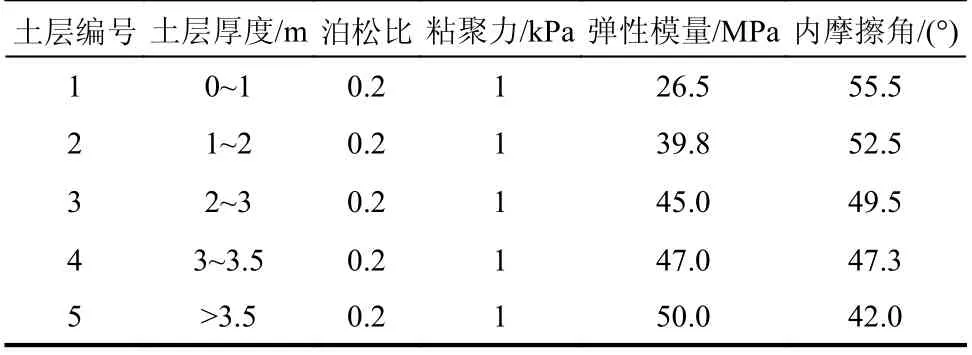
表 4 Li 模型试验土层参数[27]Table 4 Parameters for soil of Li experiment[27]

图 4 Li 模型试验模型(FLAC3D)Fig.4 Numerical model of Li experiment (FLAC3D)

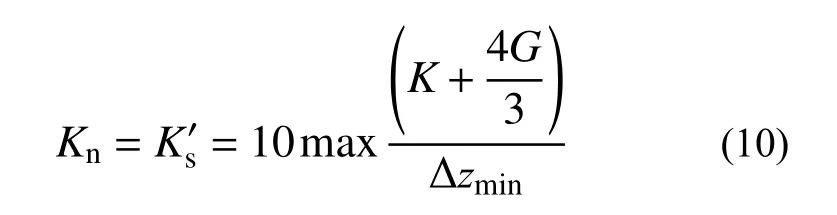
式中：K/MPa 为桩周土体的体积模量；G/MPa 为桩周土体的剪切模量；Δzmin为接触面法向连接区域上的最小尺寸。

3.1.2 FLAC3D数值模型的验证

在高于地面0.4 m 的桩截面施加0 kN～100 kN的水平荷载，将FLAC3D数值模型计算的桩顶水平位移-荷载的关系曲线、不同深度的p-y 曲线与试验结果、现有p-y 曲线的计算结果进行对比分析，如图5、图6 所示。

由图5 可知，现有p-y 曲线模型计算的桩顶水平位移偏小；但FLAC3D数值计算结果与试验实测结果吻合较好。由图6 可知，API 推荐的p-y 曲线高估了初始地基刚度，使得在小荷载情况下，API 推荐的p-y 曲线计算的桩的水平变位较实测值偏小；而FLAC3D数值模型提取的p-y 曲线与实测值基本吻合。

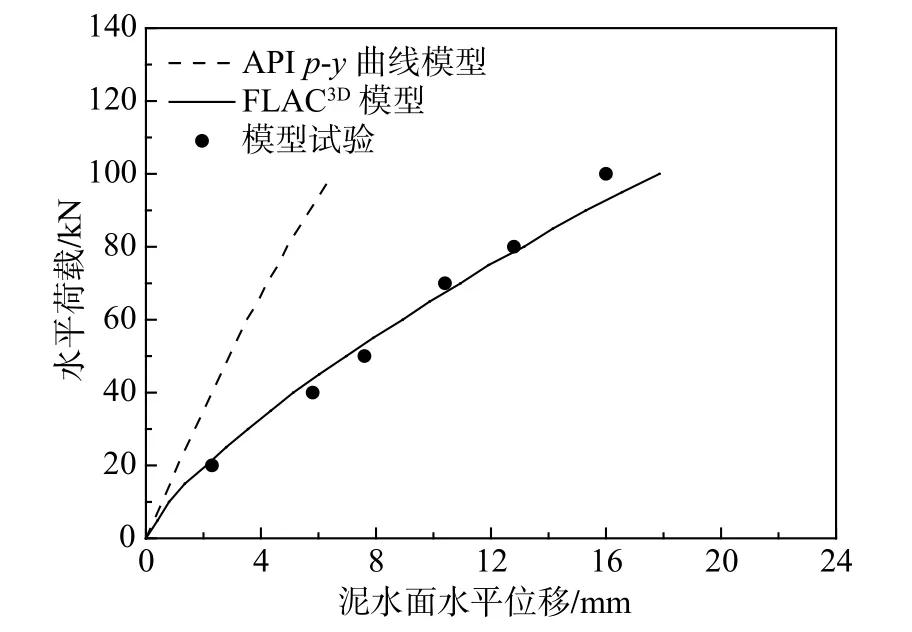
图 5 数值模拟与试验数据的对比[27]Fig.5 Comparison of numerical simulation and test data[27]

基于上述FLAC3D数值模型，在高于地面0.4 m 处的桩顶，施加水平位移荷载10 cm、16 cm 和20 cm，根据数值计算结果提取深度0.68 m(2D)、1.02 m(3D)、2.04 m(6D)的p-y 曲线进行对比，如图7 所示。由图可知，加载荷载的大小对提取的p-y 曲线初始刚度几乎无影响。因此，后续数值计算中桩顶水平位移荷载均取16 cm，方便计算结果的对比。

3.2 修正参数的确定

本节开展了非常松散、松散、中密、密实、超密的五种砂土场地下数值计算，具体土层参数如表5 所示；钢管桩长细比为6，桩径为2 m～8 m，壁厚为50 mm～80 mm。数值模型中，桩体采用弹性模型；土体采用Mohr-Coulomb 模型，同时为考虑土体弹性模量随深度的非线性，将式(5)引入土体模型中。

3.2.1 桩径影响指数的确定

提取数值模型计算中同一深度不同桩径的p-y曲线，以桩径2 m 的地基刚度K2为基准，根据式(11)对计算结果进行无量纲处理，如图8～图12所示。

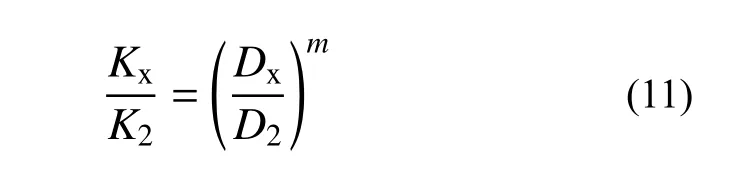
式中，Kx为桩径为Dx下的初始地基刚度。

由图8～图12 可知，超密、密实、中密场地下，无量纲地基刚度的桩径影响指数为0.5；松散、非常松散场地下，无量纲地基刚度的桩径影响指数为0.6。结果表明，桩径的改变导致桩周土体的地基模量的改变，进而引起桩周土体的应变水平的改变。

3.2.2 深度影响指数的确定

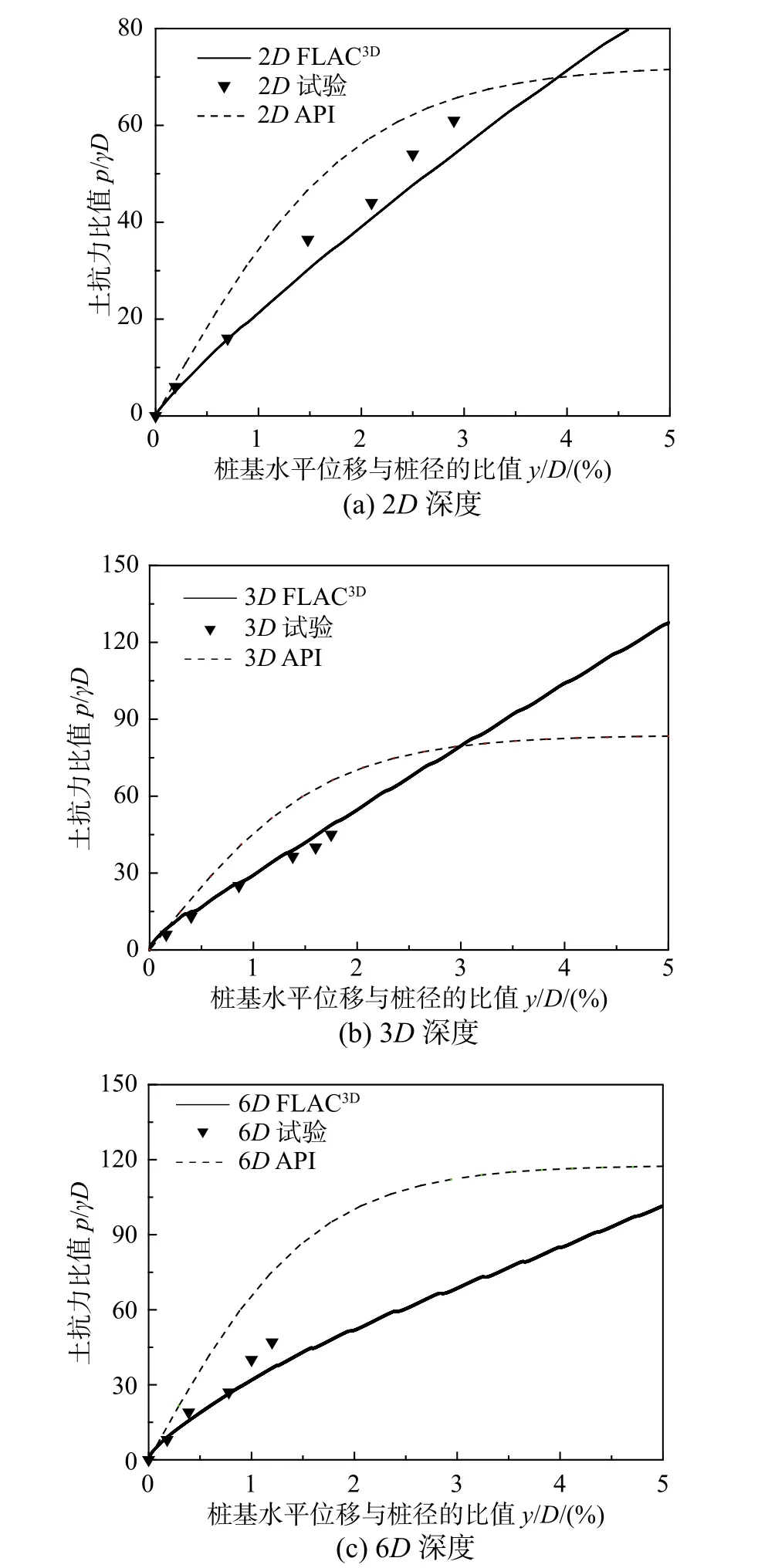
图 6 API、FLAC3D、Li 模型试验不同深度p-y 曲线的对比Fig.6 Comparison of p-y curves for API, FLAC3D, Li experiment at different depths

对提取的同一桩径不同深度的p-y 曲线，以深度1 m 的地基刚度K1为基准，根据式(12)对计算结果进行无量纲处理，同时取表5 中的弹性模量系数λ 确定的无量纲函数拟合不同场地的无量纲刚度，如图13～图17 所示。

式中：K1为深度z1为1 m 的初始地基刚度；Ky为桩径为zy下的初始地基刚度。

由图13～图17 可知，超密、密实场地下，无量纲地基刚度的深度影响指数为0.5；中密场地下，深度影响指数为0.6；松散、非常松散场地下，深度影响指数为0.65。结果表明，地基刚度的深度影响指数与表4 中的弹性模量系数λ 基本吻合，再次证明了地基刚度与弹性模量的正相关性。

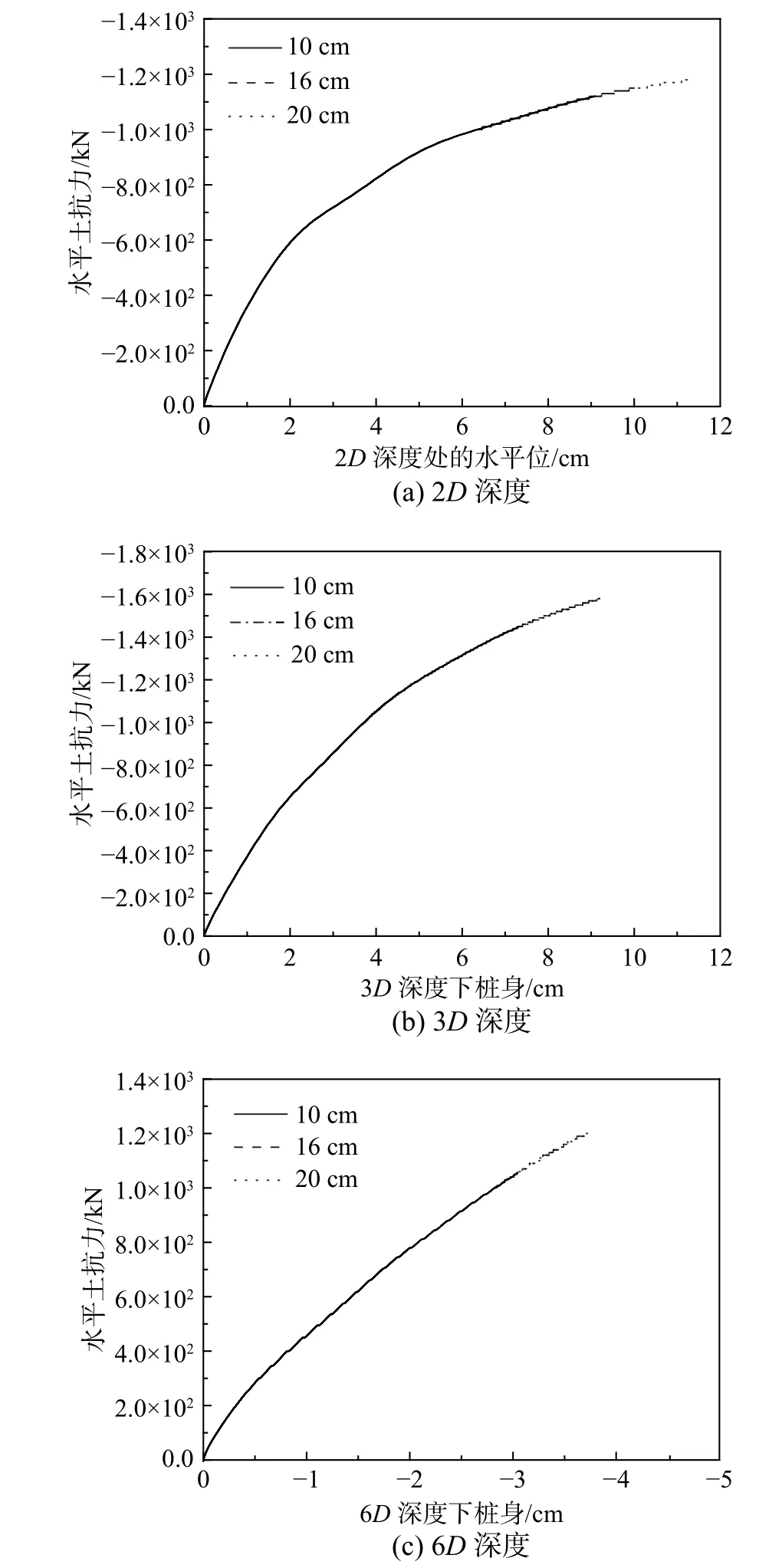
图 7 不同位移荷载下的p-y 曲线的对比Fig.7 Comparison of p-y curve under different displacement loads

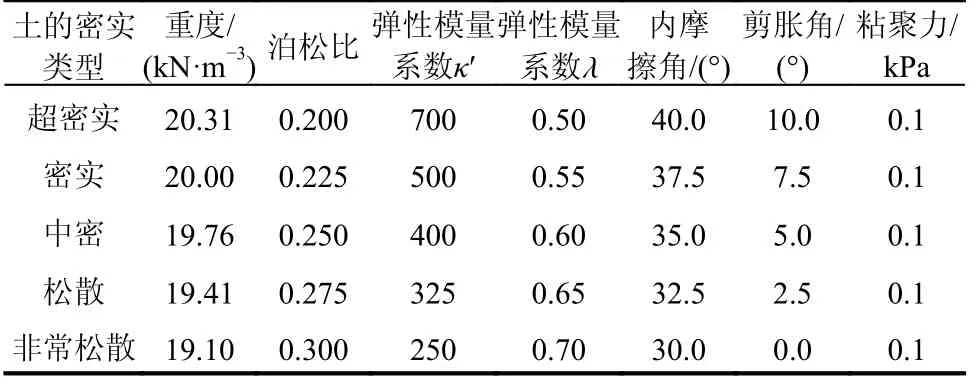
表 5 数值模拟模型中的土层参数[28]Table 5 Soil parameters of numerical simulation model[28]

3.3 修正的p-y 曲线模型

基于前述确定的修正参数建立初始地基刚度的修正模型，如表6 所示。

图 8 超密砂土场地下桩径影响指数的拟合Fig.8 Fitting value of diameter effect index under very dense sand

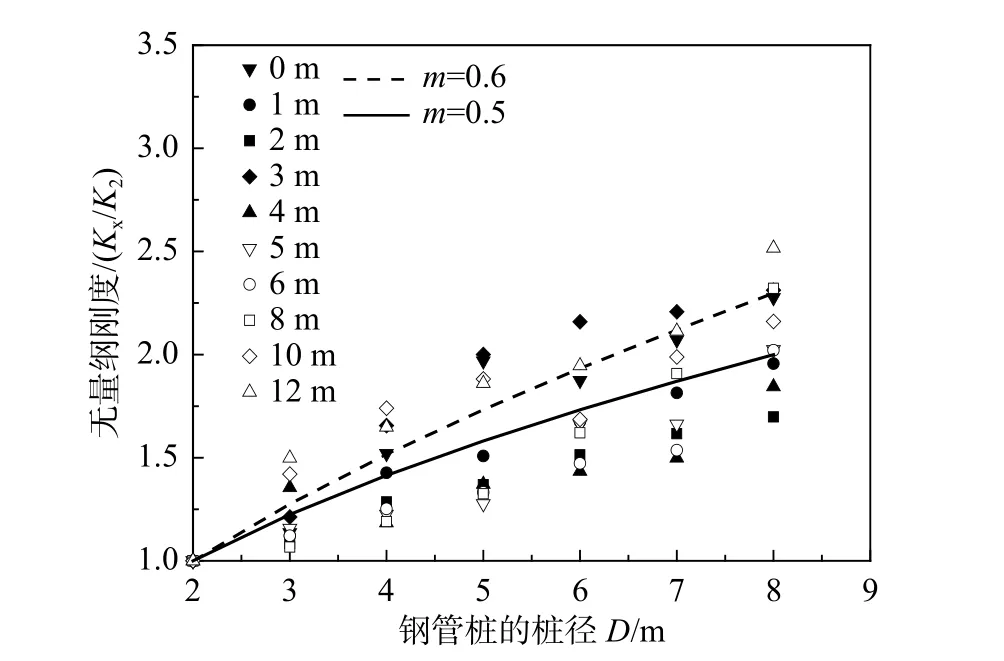
图 9 密实砂土场地下桩径影响指数的拟合Fig.9 Fitting value of diameter effect index under dense sand

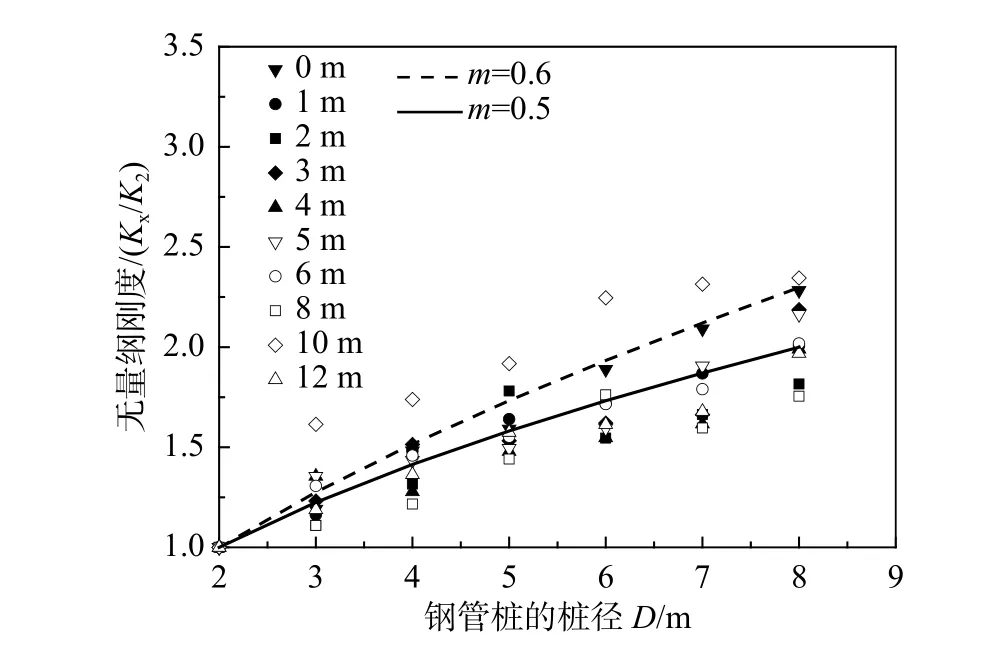
图 10 中密砂土场地下桩径影响指数的拟合Fig.10 Fitting value of diameter effect index under medium dense sand

图 11 松散砂土场地下桩径影响指数的拟合Fig.11 Fitting value of diameter effect index under loose sand

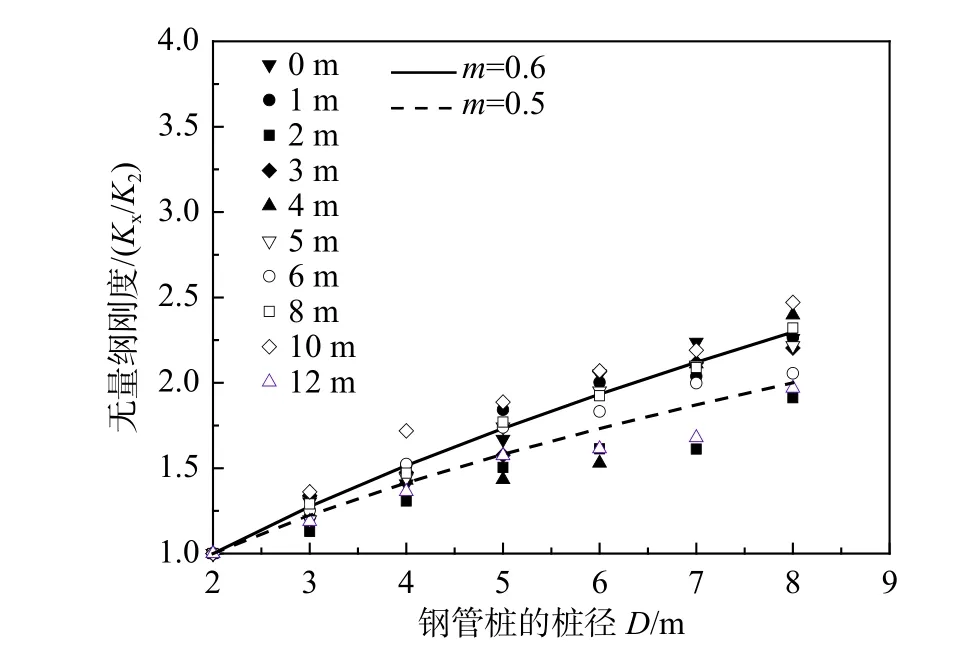
图 12 非常松散砂土场地下桩径影响指数的拟合Fig.12 Fitting value of diameter effect index under very loose sand

图 13 超密砂土场地下深度影响指数的拟合Fig.13 Fitting value of depth effect index under very dense sand

将表6 中的修正地基刚度替换式(1)的现有地基刚度，形成修正的p-y 曲线模型，具体如下：

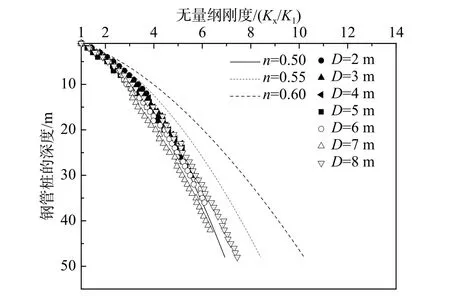
图 14 密实砂土场地下深度影响指数的拟合Fig.14 Fitting value of depth effect index under dense sand

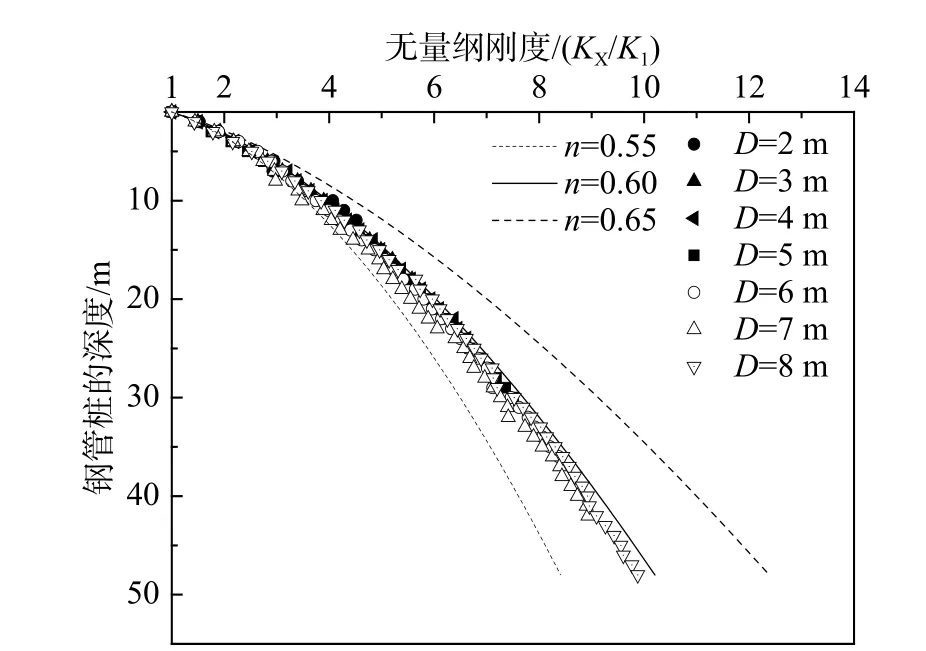
图 15 中密砂土场地下深度影响指数的拟合Fig.15 Fitting value of depth effect index under medium sand

图 16 松散砂土场地下深度影响指数的拟合Fig.16 Fitting value of depth effect index under loose sand

4 修正p-y 曲线模型的验证

初始地基反力模量的选取直接影响了p-y 曲线模型的计算值，Georgiadis 等[29]、Kim 等[30]通过试验验证了表2 中Terzaghi[19]推荐的地基反力模量取值的合理性。因此本文初始地基刚度的计算采用表2 中的地基反力模量推荐值。

本文采用MATLAB 编制了修正初始地基刚度后的p-y 曲线模型的有限元计算程序，分析了两个砂土场地的模型试验，并与模型试验实测结果、API 推荐的p-y 曲线模型进行了对比分析。

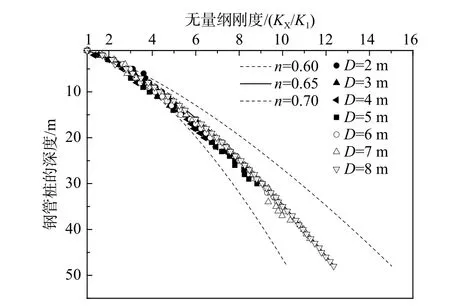
图 17 非常松散砂土场地下深度影响指数的拟合Fig.17 Fitting value of depth effect index under very loose sand

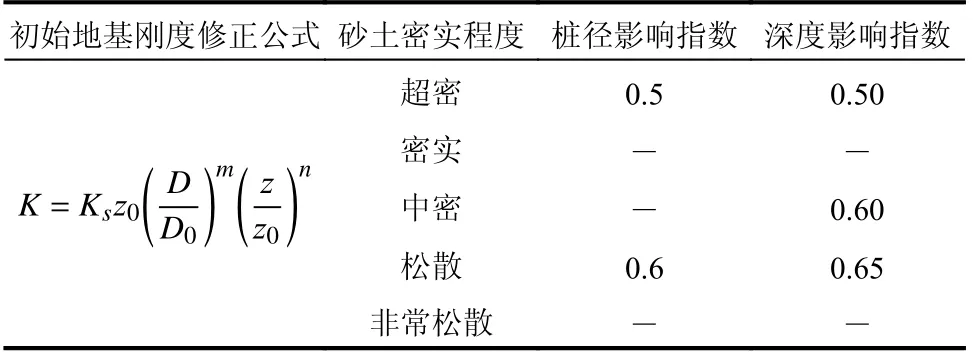
表 6 初始地基刚度的修正模型Table 6 Modified model of initial stiffness of subgrade

4.1 案例验证1

Prasad 和Chari[31]在直径1.83 m、高2.00 m的圆柱形模型中，开展了相对密实度25%、50%、75%三种不同场地下的刚性桩模型试验。其中钢管桩桩径0.102 m、埋深0.612 m，钢管桩弹性模量210 GPa。

相对密实度为25%的土体内摩擦角为33.3°，土体重度为16.5 kN/m3；相对密实度为50%的土体内摩擦角为39°，土体重度为17.3 kN/m3；相对密实度为75%的土体内摩擦角为43°，土体重度为18.3 kN/m3。计算结果如图18 所示。

由图18 分析可知，在荷载较小情况下，API采用的p-y 曲线模型计算的位移小于实测值，随着荷载的增大，API 采用的p-y 曲线模型计算结果与实测结果差异越来越显著；而修正p-y 曲线模型与实测结果基本吻合；在密实度75%的场地下，本文修正模型与已有的修正模型相比，本文修正模型与实测结果吻合较好。

4.2 案例验证2

Sφrensen 等[32]在内径2.1 m、高度2.5 m 的圆柱形模型箱中，开展了长细比为5 的刚性桩模型试验。模型试验中，钢管桩桩径为0.1 m、壁厚为0.005 m、弹性模量为210 GPa；土体相对密实度为80%，土粒相对密度为2.64。计算结果如图19所示。

图 18 修正p-y 模型与实测结果的桩顶变形对比[31]Fig.18 Comparison of modified p-y model and measured results for pile head deflection[31]

图 19 桩顶荷载-变形曲线的对比[32]Fig.19 Comparison of pile head force-deflection curves[32]

由图分析可知，API 采用的p-y 曲线模型计算结果与试验实测结果差异较大；且与已有修正模型相比，本文修正p-y 曲线模型与实测结果吻合较好。

4.3 案例验证3

Ubilla 等[33]开展了加速度为 70 g 的水平受荷钢桩离心试验。其原型为桩径4.4 m、抗弯刚度为8.2×108kN/m2，桩周土体为12 m 密实度50%的砂土、5 m 软粘土、8 m 密实度为75%的砂土。该模型桩为刚性桩且粘土层位于旋转点附近，因此上下砂土层的水平土抗力对该桩基的水平承载能力起控制作用。采用本文修正模型计算该模型桩的桩顶水平位移，并与已有修正p-y 曲线模型、API p-y 曲线模型进行对比，如图20 所示。

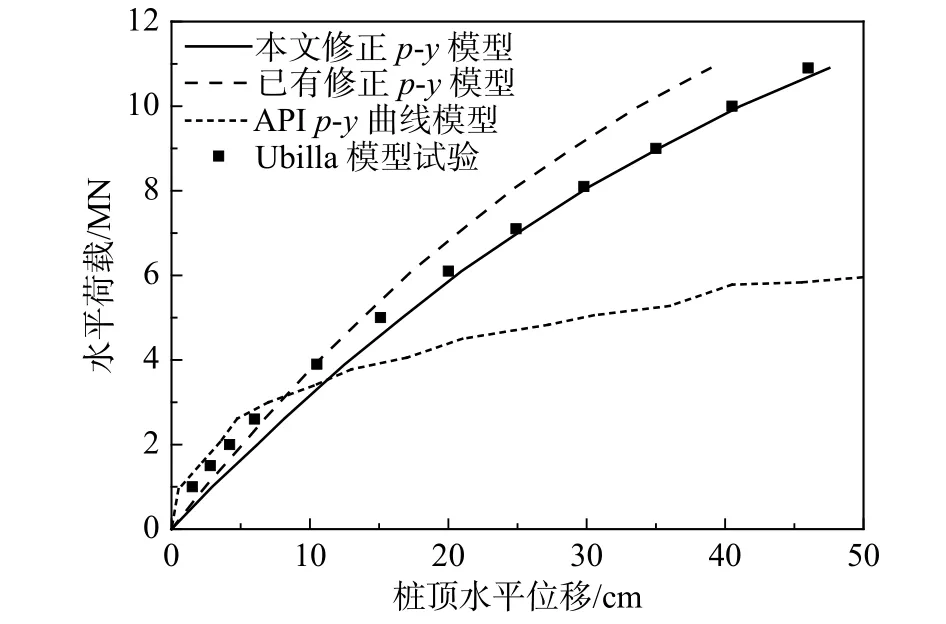
图 20 修正模型的桩顶荷载-变形曲线与实测结果对比[33]Fig.20 Comparison of modified model and measured results for pile head force-deflection curves[33]

由图20 分析可知，现有p-y 曲线模型计算结果与试验实测结果差异较大；在荷载较大时，已有修正模型计算结果与试验实测结果误差较大，而本文修正模模型与实测结果吻合较好，这是由于已有修正模型未考虑场地变异性的影响，上下两层砂土的地基模量的修正参数均取0.5、0.6；而本文修正模型地基模量修正参数上层砂土取0.5、0.6，下层砂土的地基模量修正参数取0.5、0.5。

5 结论

为克服传统p-y 曲线模型计算刚性桩荷载-位移关系的不足，本文结合既有的研究，探讨了桩的桩径影响、土体的深度对传统p-y 曲线的影响机制。基于FLAC3D整体桩-土数值计算模型，系统地分析了超密、密实、中密、松散、非常松散五种场地下的p-y 曲线，从而建立了修正的p-y 曲线模型，并通过案例验证了本文修正模型的合理性。通过本文研究，得出以下结论：

(1)在刚性桩的水平荷载-变形关系计算中，传统p-y 曲线模型对初始地基刚度的高估是引起计算误差的主要因素。

(2)桩径的变化引起土体应变水平的变化，是大直径桩的桩径变化对地基刚度产生影响的主要原因。超密、密实、中密场地下，桩径影响指数为0.5；松散和非常松散场地下，桩径影响指数为0.6。

(3)土体地基刚度与弹性模量存在正相关性。超密、密实场地下，地基刚度的深度影响指数为0.5；中密场地下，深度影响指数为0.6；松散、非常松散场地下，深度影响指数为0.65。

(4)通过FLAC3D 数值计算，反算出桩的桩径影响指数和土体深度影响指数，建立了修正的py 曲线模型，且修正模型的计算结果更加接近实测值，改善了传统p-y 曲线对大直径钢管桩的计算误差。

(5)本文建立的修正的p-y 曲线模型，未考虑加载、卸载、荷载循环效应对桩-土相互作用的影响，对循环荷载作用下大直径单桩基础的水平变形特性有待进一步深入研究。