基于长短时记忆神经网络的大跨拱桥温度-位移相关模型建立方法

郑秋怡，周广东，刘定坤

(河海大学土木与交通学院，南京 210098)

大跨桥梁在长期服役过程中，环境作用与运营荷载的耦合作用，导致结构性能不断退化甚至出现灾变垮塌，因此，如何保证大跨桥梁服役安全是桥梁工程领域的重要任务[1-2]。位移能够表征大跨桥梁由于局部损伤或构件破坏引起的受力性能变化，是评估大跨桥梁服役安全的有效指标[3-5]。然而，不仅损伤会导致大跨桥梁位移变化，温度也会引起显著的位移变化。已有研究表明，日本明石海峡大桥单位温度变化引起的挠度可达68.7 mm[6]，香港青马大桥由温度产生的竖向位移波动年幅值超过2000 mm[7]。由此可见，错误估计温度引起的位移不仅会降低大跨桥梁安全评估结果的可靠性，甚至可能得出错误的结论。因此，有必要深入研究温度引起的大跨桥梁位移响应。

基于同步实测的温度和位移数据，建立温度与位移的关联模型，是估计大跨桥梁热位移的理想途径。然而，引起大跨桥梁热位移的温度变量，不仅有构件截面的有效温度，还有构件之间的温差，呈现多元性[8]。不仅如此，温度和位移之间还可能具有非线性特征。这些因素使得线性拟合、非线性拟合等传统方法难以准确估计温度与位移的映射关系。神经网络具有很强的非线性映射、高度自学习和自适应能力，是建立多元温度-位移相关模型的有效方法。近年来，国内外学者采用神经网络对温度-位移相关模型进行了初步研究。陈德伟等[9]采用误差反向传播(BP)神经网络建立了大佛寺长江大桥温度和挠度的相关模型，验证了神经网络预测桥梁挠度的可行性。胡铁明等[10]利用BP 神经网络建立了辽河特大桥温度和支座位移的模型，并将其应用于结构损伤预警。Zhou 等[11]采用平均影响值法提取主要热变量，基于BP 神经网络建立了大跨拱桥竖向变形与温度变量的相关模型。虽然单隐含层神经网络可以模拟任何非线性连续函数，但随着数据量的增大，增加隐含层的数量可以有效提高模型的预测精度。Wen 等[12]采用双隐含层BP 神经网络预测了温度作用下桥梁的挠度行为。Zhao 等[13]提出了一种基于三隐含层BP 神经网络的挠度预测方法。另外，戴建彪等[14]提出了一种径向基神经网络模型，用于预测苏通长江大桥的温度变形。

虽然已有研究在温度-位移相关模型建立方面探索到了一些途径，但是这些模型不能有效计入位移的时滞效应[15]，导致模型的误差难以接受。同时，在面对大跨桥梁多年累积的超长数据序列时，这些模型存在训练难度高、计算效率低的缺点。长短时记忆(LSTM)神经网络具有描述时间序列延迟特征和处理超长数据序列的能力。Kok 等[16]基于LSTM 神经网络，利用物联网智能城市数据来预测未来智能城市的空气质量值；曲悦等[17]采用LSTM 神经网络建立了气象数据-PM2.5 相关模型，预测了未来一小时的PM2.5 污染值；张冬雯等[18]以空气污染物为输入，空气质量指数为输出，建立了LSTM 神经网络空气质量预测模型；Awan 等[19]以空气污染、大气参数和交通强度作为LSTM 神经网络的输入层，实现了交通流的准确预测；王国松等[20]选取21 个变量作为预报因子，利用LSTM 神经网络对中国近海5 个代表站进行了风速预测。已有研究结果表明，LSTM 神经网络是解决时滞效应和海量监测数据的有效方法。但是其在温度-位移相关模型建立方面的应用，还未见报道。

本文以LSTM 神经网络为基础，并进一步利用自适应矩估计方法对网络进行优化，再引入丢弃正则化技术提升网络的预测能力，提出了一种基于LSTM 神经网络的大跨桥梁温度-位移相关模型建立方法，并将其应用于一座三跨连续系杆拱桥的热位移分析。研究结果可为大跨桥梁温度-位移相关模型的建立和基于位移的大跨桥梁性能评估提供帮助。

1 温度-位移相关模型建立方法

1.1 LSTM 神经网络

传统BP 神经网络包括输入层、隐含层和输出层，仅在不同隐含层之间建立权连接，通过激活函数控制输出，无法挖掘时间序列数据的内部模式，在长距离传递信息时容易产生梯度消失和梯度爆炸等问题，适用于处理前后没有关联的数据[21]。

LSTM 神经网络包含输入层、LSTM 层(隐含层)和输出层，通过在同一隐含层神经元之间增加权连接引入定向循环，其输出不仅依赖于当前的输入，还与前期的输入(又称记忆)有关。因此，LSTM 神经网络通过捕捉不同变量之间的长期依赖关系，不仅有效提升了网络的精度，还能够处理和预测时间序列中的延迟事件[22]，特别适合处理前后存在关联的超长数据序列，比如长期实测温度序列、长期实测位移序列等。

LSTM 神经网络的结构如图1 所示，LSTM 细胞是隐含层的核心部分，用来记忆长时间的输入信息，并通过输入门、遗忘门和输出门控制信息流。将LSTM 细胞按时间展开，可以清晰展示LSTM 细胞的结构，如图1 所示[23]。输入门、遗忘门和输出门通过非线性激活函数进行控制，输出值在0～1 之间，0 表示不通过任何信息，1 表示信息全部通过。LSTM 细胞的输入包含上一时刻的细胞状态ct-1、上一时刻的细胞输出ht-1和当前时刻的网络输入xt，输出包含当前时刻的细胞状态ct、当前时刻的细胞输出ht和当前时刻的网络输出yt。LSTM 细胞工作时，首先读取xt和ht-1，经过遗忘门后输出ft，ft再与ct-1相乘得到第一个中间结果at；然后，xt和ht-1经过输入门后输出it，同时xt和ht-1经过tanh 激活后，与it相乘得到第二个中间结果bt，两个中间结果at和bt相加得到ct；最后，xt和ht-1经过输出门后输出ot，ot与经过tanh 激活后的ct相乘得到ht，ht通过激活函数拟合目标输出yt。正向传播结束后，LSTM 细胞以最小化损失函数为目标，基于优化方法反向传播误差更新权值。在t 时刻，LSTM 细胞的更新规则如下式所示：

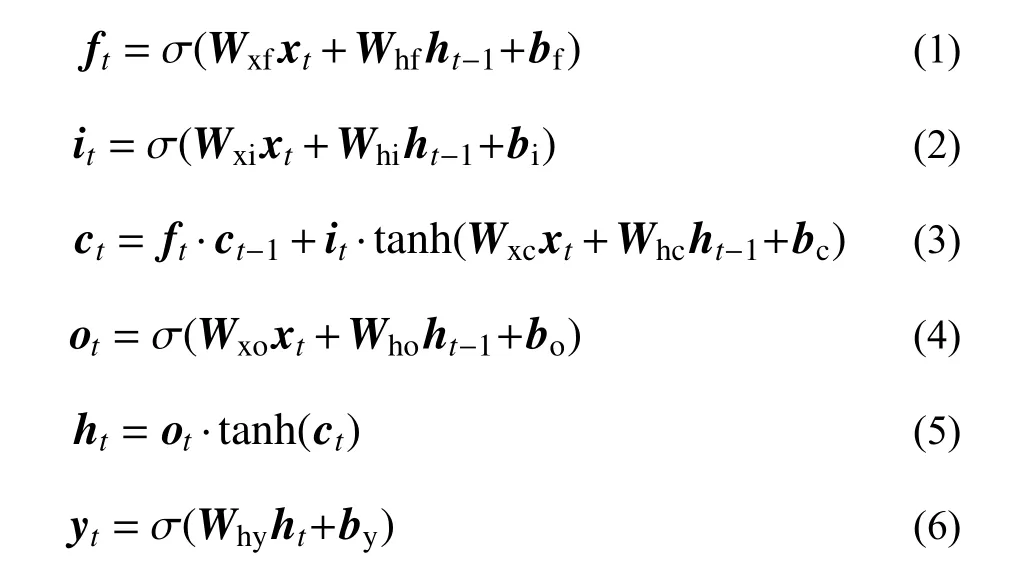
式中：下标f 、 i 、 o分别为遗忘门、输入门和输出门；σ(·)为非线性激活函数，一般选择sigmoid 函数；Wxf、Whf、Wxi、Whi、Wxc、Whc、Wxo、Who和Why为权重矩阵； bf、 bi、 bc、 bo和 by为偏置矩阵；ht-1和 ht分别为LSTM 细胞上一时刻和当前时刻的输出； xt为当前时刻的网络输入； yt为当前时刻的网络输出；tanh(·)为双曲正切函数。

图 1 LSTM 神经网络结构图Fig.1 Structure diagram of LSTM neural network

1.2 LSTM 神经网络超参数优选

1.2.1 损失函数

损失函数用来衡量预测值与实测值之间的差异程度，是更新网络参数的重要依据。常用的损失函数有均方误差和平均绝对误差。当神经网络训练集中存在异常值时，均方误差会给异常值赋予很大的权重，导致模型的预测能力下降。相比之下，平均绝对误差对异常值具有更好的鲁棒性，定义如下[24]：

式中： W 为LSTM 神经网络中所有权重矩阵的集合；n 为训练样本长度；yi为第i 个实测值；f(xi)为第i 个预测值。损失函数的值越小，表明模型的拟 合程度越好。

1.2.2 优化器

优化器直接影响网络的预测能力。传统的随机梯度下降法在网络训练过程中很难确定合适的初始学习率，只能根据预先指定的规则进行调整，且相同的学习率被应用于所有参数。自适应矩估计方法可以动态调节每个参数的学习率，具有很高的计算效率和较低的内存需求。该方法的参数更新公式如下[25]：

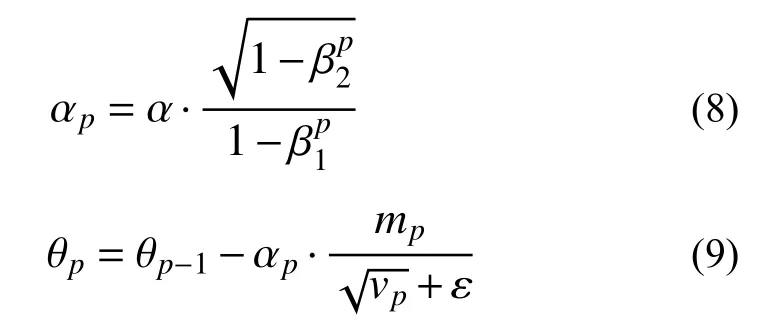
式中： p 为迭代次数； α为初始学习率； β1和 β2为指数衰减率，可取为0.9 和0.999； θ为网络中待更新的权重和偏置； ε为调整系数，可取为10-8；mp和 vp分别为梯度的一阶和二阶矩估计。

1.2.3 正则化

过拟合是神经网络在处理大量数据时经常出现的问题，会大幅降低网络的预测能力。与L1、L2 正则化不同，丢弃正则化通过改变网络本身，而不依赖于损失函数的修改，能够显著提升神经网络的预测精度。丢弃正则化通过在不同网络层中添加丢弃层并设定丢弃概率而实现。丢弃概率模型为[26]：

式中， r(l)为第l层中服从伯努利分布Bernoulli(η)的随机变量集合。

在神经网络训练过程中，将 r(l)和第l层的输出向量相乘，使得输出向量中的部分元素变为0，然后将此结果作为第l+1层的输入向量，最后经过非线性激活函数，得到第l+1层的输出向量，其公式如下：

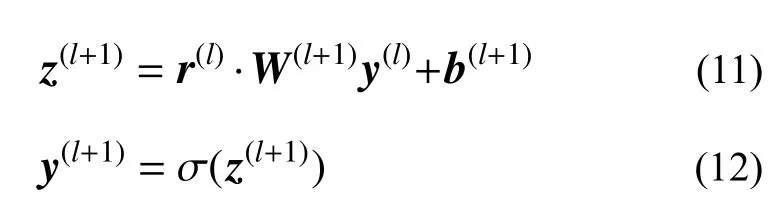
式中：z(l+1)为第l+1层的输入向量； y(l)和y(l+1)分别为第l层和第l+1层的输出向量；W(l+1)、b(l+1)分别为第l+1层的权重和偏置矩阵。

1.3 温度-位移非线性模型建立流程

温度-位移LSTM 神经网络模型建立流程如图2 所示。

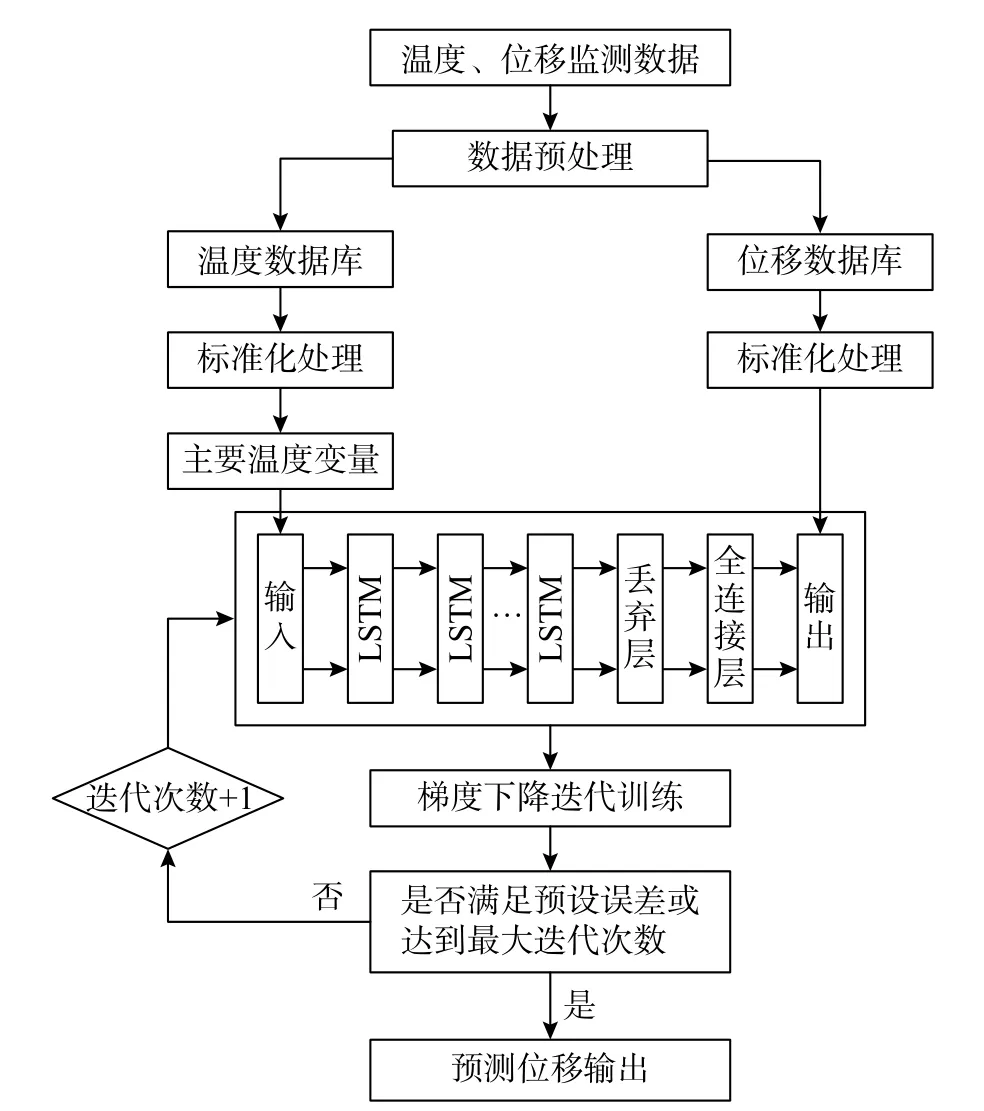
图 2 LSTM 神经网络预测流程图Fig.2 LSTM neural network prediction flow chart

1) 预处理温度和位移原始监测数据，主要包括剔除异常数据、建立温度和位移样本数据库；

2) 利用z-score 函数对实测数据进行特征标准化处理，消除样本数据量纲的影响：

式中： x 和 x*分别为原始数据和标准化数据； μ和s分别为每列数据的均值和标准差；

3) 提取主要温度变量，降低温度变量间的信息重叠性，提升模型运行效率；

4) 建立由LSTM 层、全连接层和丢弃层组成的温度-位移LSTM 神经网络，选取合适的参数进行网络初始化；

5) 以主要温度变量作为输入、位移作为输出，采用自适应矩估计方法进行梯度下降迭代训练，不断更新权重和偏置矩阵；

6) 利用平均绝对误差作为损失函数来评价网络的误差。若误差小于预先设定的阈值或迭代次数达到最大迭代次数，则结束训练，输出预测位移值。否则，返回第5)步继续训练，直至满足终止条件。

2 算例分析

以一座三跨连续系杆拱桥的温度和位移同步监测数据为例，讨论了影响该桥热位移的主要温度变量，并分别采用本文的LSTM 神经网络和BP神经网络建立温度-位移相关模型，通过对比分析验证本文方法在重构精度和预测能力方面的优势。

2.1 温度和位移同步监测

该三跨连续系杆拱桥每跨210 m，上部结构由主拱、副拱、吊索和横向支撑形成空间受力体系，如图3 所示。为了准确把握该桥的运营状态，安装了一套包括300 余只传感器的健康监测系统，用于监测运营环境(包括风、温度、湿度和地震动)和结构响应(包括振动、应变、变形和索力等)[27]。结构温度监测子系统包含60 只温度传感器，分别安装在主梁、主拱和吊索上，布设位置如图4 和图5 所示。

图4 中下标数字表示监测截面编号，括号内的数字表示传感器数量；图5 中下标表示传感器编号。温度传感器的分辨率为0.0625℃，测量范围为-55℃～125℃，采样周期为1 min。主梁竖向位移采用压力变送器进行监测，布设位置如图6所示。20 个压力变送器对称放置于主梁两侧，既可以监测竖向变形，又可以监测扭转变形。共分为两组，每组配置一个参考传感器，参考传感器位于竖向位移几乎为零的拱脚位置。压力变送器量程为1000 mm，精度为0.065%，采样频率为0.1 Hz。

图 3 某三跨连续系杆拱桥Fig.3 A three-span continuous tied arch bridge

图 4 温度传感器的布设位置Fig.4 Layout of temperature sensors on bridge

图 5 温度传感器布设位置细节图Fig.5 Detailed layout of temperature sensors

图 6 主梁竖向位移传感器的布设位置Fig.6 Layout of vertical displacement sensors on main girder

2.2 数据预处理

实测竖向位移为温度变化引起的位移、风荷载引起的位移、车辆荷载引起的静态位移、车辆荷载引起的动态位移、环境振动引起的位移、测量噪声之和。由于该座大跨拱桥刚度较大，且处于内陆地区，选取5 m/s 作为临界风速。当10 min平均风速小于5 m/s 时，认为风速引起的竖向位移可忽略不计。当风速大于5 m/s 时，同时删除温度和位移数据，从而剔除风荷载的影响。考虑温度和热位移的慢变特征，以10 min 为基本时距，对实测温度和位移进行平均，消除车辆荷载引起的动态位移、环境振动引起的位移和测量噪声的影响，同时保持温度数据和热位移数据长度的一致性[28]。进一步地，建立该桥的有限元模型并进行修正，利用动态称重系统获得的车辆荷载数据作为输入，计算车辆荷载引起的竖向静态位移，据此剔除车辆荷载引起的静态位移。

选取中跨跨中截面2013 年7 月28 日-2014 年6 月26 日共13824 组温度和位移同步监测数据作为神经网络的数据集，采用中跨跨中截面冬季(2013 年12 月20 日-25 日)和 夏季(2014 年6 月21 日-26 日)共1728 组数据作为神经网络的测试集，余下12 096 组数据作为神经网络的训练集。

计算主梁、主拱、吊索的截面有效温度(ET)、截面温度梯度(TG)和构件间温差(TD)共13 个温度变量，如表1 所示。其中，有效温度为某一桥梁构件横截面上分布的平均温度，定义如下[29]：

式中：A 为横截面面积；T(x,y)为横截面上的温度分布；x 和y 分别为横截面水平方向和竖直方向的坐标。

表 1 温度变量Table 1 Thermal variables

同一横截面上常常布置多个温度传感器，为了简化计算，根据传感器布置将横截面划分为多个区域，每个区域内布置一个传感器，并假定每个区域内的温度相同且等于相应传感器的测值，有效温度的计算可以简化为[29]：

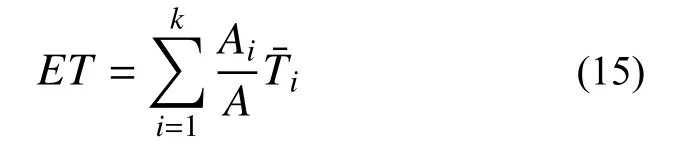
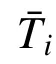
2.3 温度-位移相关性分析

图7 给出了该座大跨拱桥中跨跨中截面上游侧2013 年8 月3 日～9 日的主拱有效温度和竖向位移时程图。由图可见，随着主拱有效温度的升高，竖向位移也逐渐增大。同时，竖向位移达到最大值的时间滞后于主拱有效温度，存在明显的时滞效应。

图 7 大跨拱桥温度和竖向位移时程曲线Fig.7 Time history of temperature and displacement on long-span arch bridge

同步监测的温度和位移数据表明，拱桥主梁跨中竖向位移与有效温度有显著的非线性相关性，竖向位移随着有效温度的升高而增大，如图8所示。这主要是由于随着主拱、吊索和主梁有效温度的升高，主拱轴线、吊索和主梁伸长，主梁的预拱度被释放，同时迫使两个拱脚向外移动，进而拉低拱顶，引起主梁跨中的竖向位移。

拱桥主梁跨中竖向位移与温差呈线性相关性，竖向位移随着温差的增大而增大，如图9 所示。其原因在于，吊索与主梁之间的正温差使得吊索伸长，主拱与主梁之间的正温差导致主拱轴线伸长，进而引起主梁跨中的竖向位移。

拱桥主梁跨中竖向位移随着主拱温度梯度的增大而增大，具有线性相关特征，如图10 所示。拱桥主梁跨中竖向位移与主梁温度梯度的相关性较弱。主拱温度梯度导致主拱上表面伸长，进而拉伸主拱的轴线，使得两个拱脚向外移动，主梁的预拱度减小，引起主梁跨中的竖向位移。

由于有效温度、温差和温度梯度对竖向位移的影响程度未知，传统线性拟合和非线性拟合难以给出温度与位移的多元非线性关联模型。

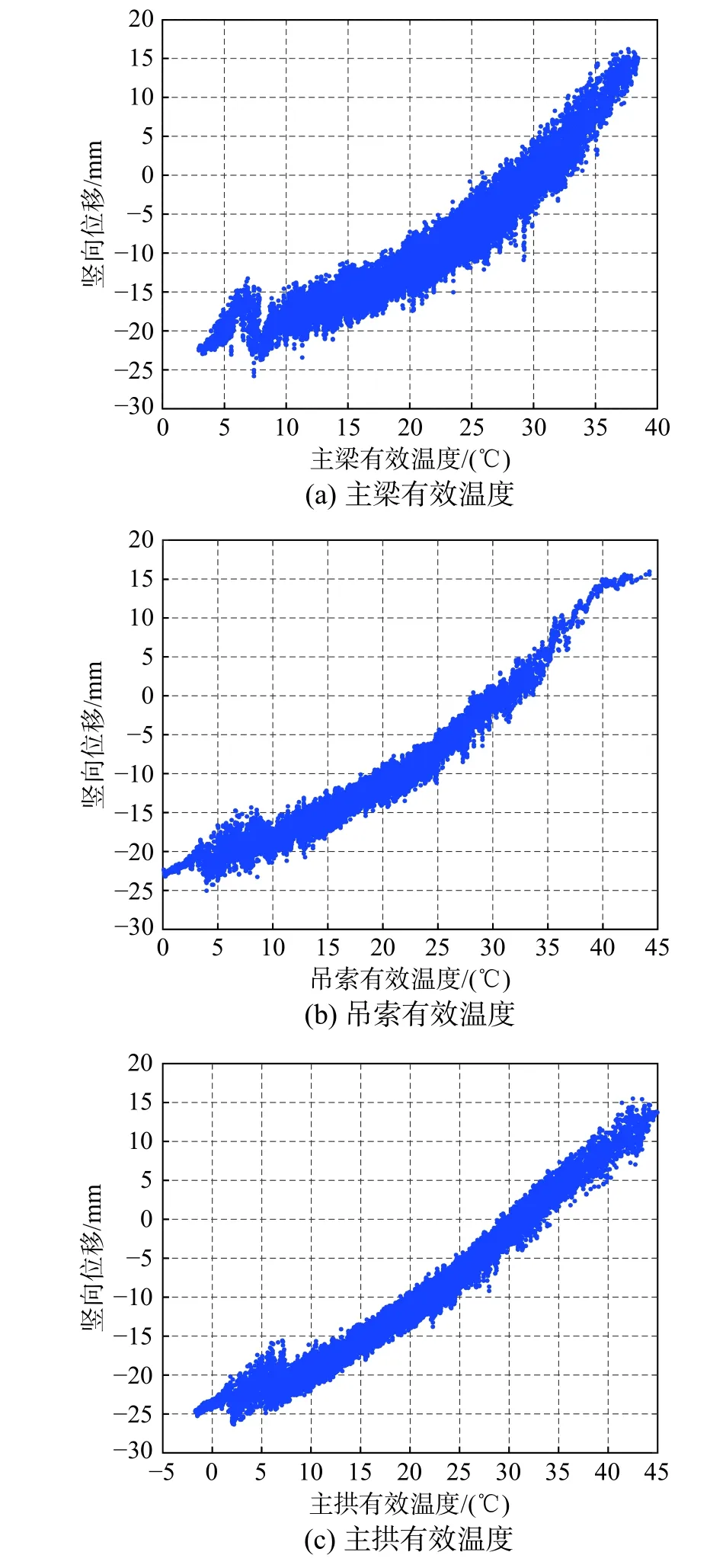
图 8 有效温度与竖向位移的相关性Fig.8 Correlation between effective temperature and vertical displacement

图 9 温差与竖向位移的相关性Fig.9 Correlation between temperature difference and vertical displacement

图 10 温度梯度与竖向位移的相关性Fig.10 Correlation between temperature gradient and vertical displacement

2.4 大跨拱桥主要温度变量筛选

利用皮尔逊相关系数对表1 中的13 个温度变量进行相关性分析，各变量间的相关系数如图11所示，取值范围在-1～1 之间。由图可见，左上方区域主梁有效温度、主拱有效温度和吊索有效温度的相关系数均接近1，呈高度正相关关系；主拱与主梁的温差和有效温度的相关系数在-0.8～-0.5 之间，呈显著负相关关系。由此可见，13 个温度变量中，某些变量之间存在较强的相关性。

图 11 不同温度变量的相关系数Fig.11 Correlation coefficient between different thermal variables

由于温度变量之间的相关性，并不是所有温度变量都对位移有重要影响。因此，找出影响主梁竖向位移的主要热变量，并进行针对性监测，可以有效降低健康监测系统的成本。以13 个温度变量作为输入，中跨跨中的竖向位移作为输出，建立多元温度-位移的LSTM 神经网络模型。采用预测结果的平均绝对百分比误差作为评价指标进行主要温度变量筛选。平均绝对百分比误差的计算公式为：

表2 列出了删除不同温度变量后，温度-位移LSTM 神经网络模型的平均绝对百分比误差以及平均绝对百分比误差的增幅。其中，第一组为全部温度变量作为输入时温度-位移LSTM 神经网络模型的平均绝对百分比误差。将误差增幅2%作为筛选阈值，由表2 可得，ETA1、ETA2、TDAG1、TDAG2为影响主梁竖向位移的主要温度变量。

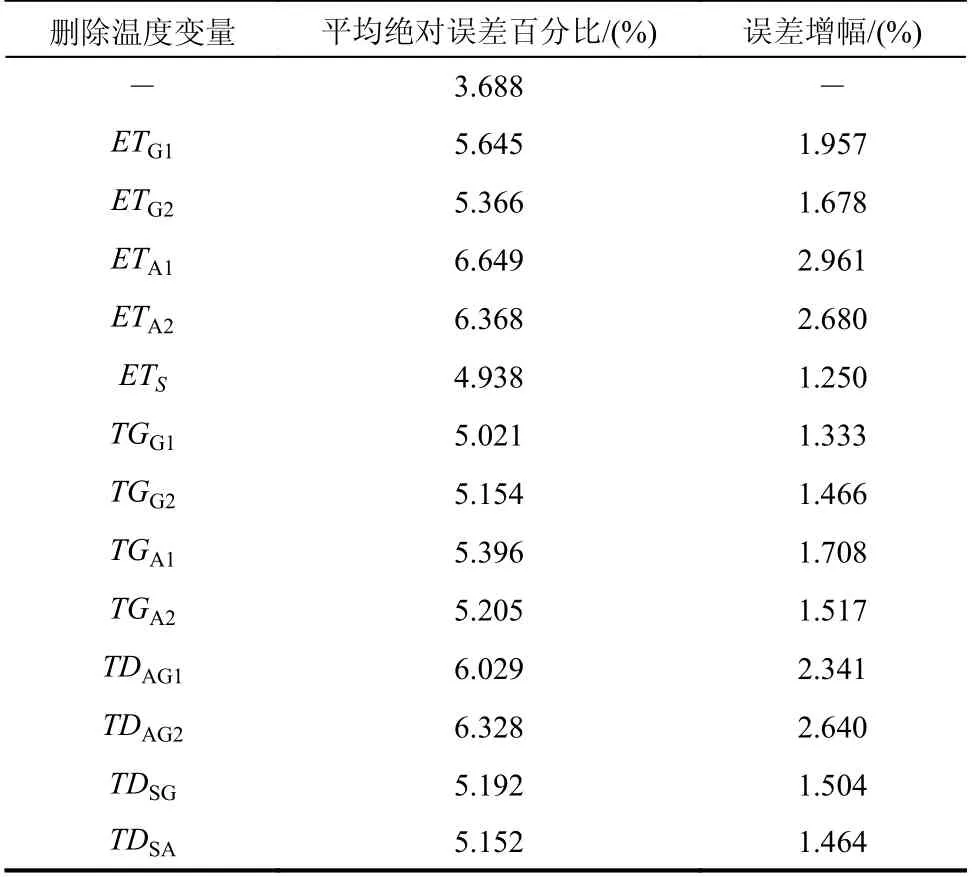
表 2 不同温度变量对位移预测值的影响程度Table 2 Influence of different thermal variables on predicted displacement values

2.5 模型的重构能力

以ETA1、ETA2、TDAG1、TDAG2作为输入，中跨跨中的竖向位移作为输出，分别建立多元温度-位移的LSTM 神经网络模型和BP 神经网络模型。采用第1 节的方法，建立包含2 个LSTM 层、1 个全连接层和1 个丢弃层的LSTM 神经网络模型。采用平均绝对误差作为损失函数进行梯度下降迭代训练，初始学习率设为0.001。丢弃层在训练中按照伯努利分布以50%的概率随机断开LSTM 层和全连接层中15 个神经元的连接，防止过拟合。每层输出进行批量标准化处理，设定每个批量为64 组数据。BP 神经网络模型包含2 个隐含层，每个隐含层含有10 个神经元，采用L-M算法进行训练，引入提前停止技术防止过拟合。

选取冬季(2013 年12 月1 日-6 日)和夏季(2014 年6 月3 日-8 日)共1728 组数据评价模型的重构能力。图12 为LSTM 神经网络模型和BP神经网络模型计算得到的重构位移值。从图中可以看出，LSTM 神经网络模型的重构位移值与实测位移值吻合良好，而BP 神经网络模型的重构位移值与实测位移值存在较大的偏差。进一步采用均方根误差、平均绝对误差、平均相对误差和相关系数对模型的重构能力进行定量评价[30-31]，计算结果如表3 所示。两种神经网络模型的相关系数均接近1，表明重构位移值和实测位移值均具有很好的相关性。两种模型在夏季的平均相对误差均超过了10%，这是由于夏季桥梁的上拱和下挠会经过位移零点，较小的预测误差也会产生巨大的相对误差。但是，相比于BP 神经网络模型，LSTM神经网络模型冬季的均方根误差、平均绝对误差、平均相对误差分别降低了47.5%、43.9%、44.7%，夏季的均方根误差、平均绝对误差、平均相对误差分别降低了41.9%、46.5%、48.9%。因此，LSTM神经网络模型具有更强的重构能力。

图 12 两种模型的重构能力对比Fig.12 Comparison of reproduction capability between two models

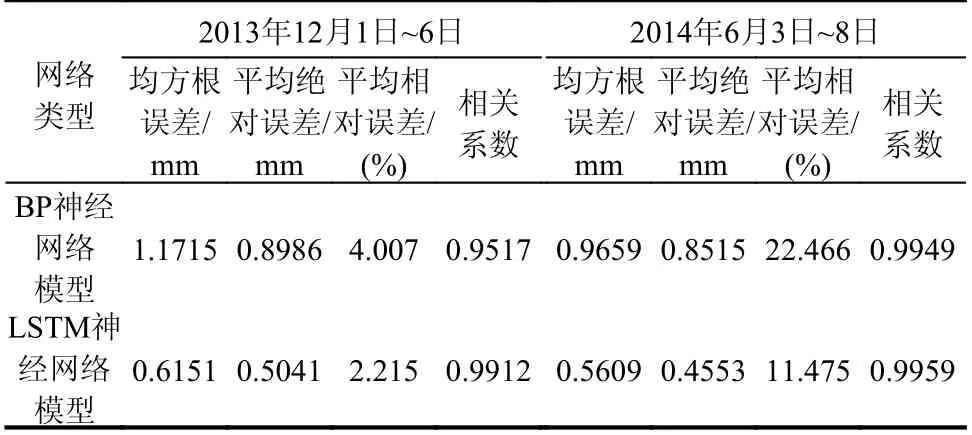
表 3 两种模型重构结果的误差及与实测结果的相关性Table 3 Error and correlation between reproduced and measured values of two models

2.6 模型的预测能力

两种温度-位移相关模型计算得到的预测位移值如图13 所示。从图中可以看出，LSTM 神经网络模型的预测位移值明显优于BP 神经网络模型的预测结果。在夏季第四天峰值位移处，BP 神经网络模型的相对误差高达74.1%，而LSTM 神经网络模型的相对误差仅为3.0%。同样采用均方根误差、平均绝对误差、平均相对误差和相关系数来评价模型的预测能力，其结果如表4 所示。LSTM神经网络模型的相关系数更接近1，冬季的均方根误差和平均绝对误差比BP 神经网络模型分别降低了41.4%和36.7%，夏季的均方根误差和平均绝对误差比BP 神经网络模型分别降低了44.7%和47.8%，两个季节的平均相对误差均在5%以内，表明LSTM 神经网络模型的预测误差更小，具有更强的预测能力。

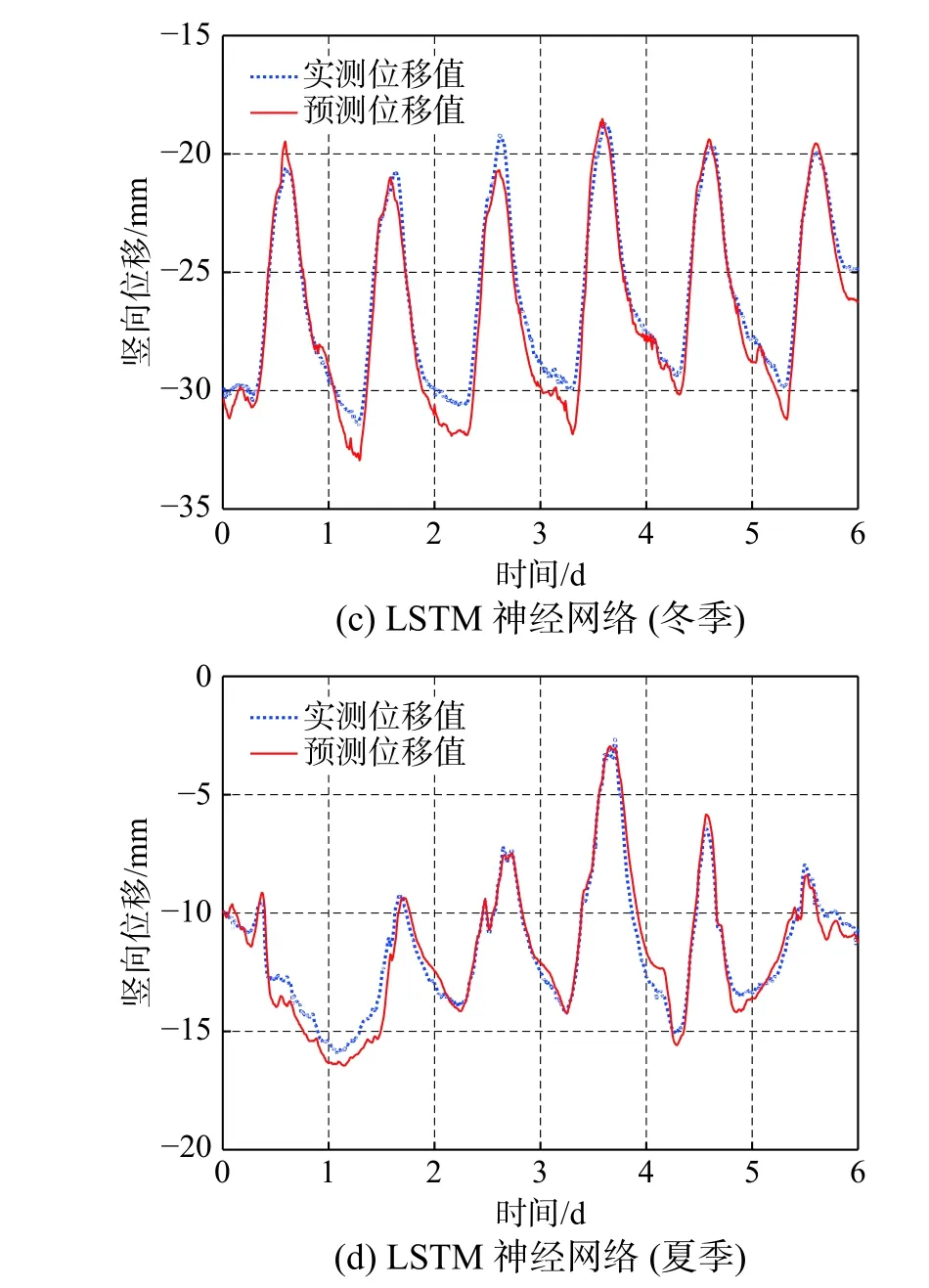
图 13 两种模型的预测能力对比Fig.13 Comparison of prediction capability between two models

表 4 两种模型预测结果的误差及与实测结果的相关性Table 4 Error and correlation between predicted and measured values of two models

进一步分析LSTM 神经网络模型预测误差的统计特征，如图14 所示。冬季的预测误差范围为-1.981 mm～1.265 mm，80%的误差集中在-1.3 mm～0.4 mm 区间内，夏季的预测误差范围为-1.621 mm～2.218 mm，75%的误差集中在-0.9 mm～0.7 mm 区间内，完全满足工程需求。由此可见，虽然LSTM神经网络模型只利用主要温度变量作为输入，却依然保持了较高的预测精度。因此，在量化温度对位移的影响时，只需计入ETA1、ETA2、TDAG1、TDAG2这4 个温度变量；在进行大跨拱桥温度监测时，仅需在主拱和主梁上布设温度传感器。

图 14 LSTM 模型预测误差概率统计图Fig.14 Probability statistical chart of predicted error of LSTM model

3 结论

大跨桥梁在服役期间的位移变化不可避免地会受到温度的影响，建立温度-位移相关模型能够将温度引起的位移从实测总位移中剔除，凸显结构损伤或劣化引起的位移改变，从而更敏感地发现结构的异常状态。本文提出了一种基于LSTM神经网络建立多元温度-位移相关模型的方法，主要结论有：

(1) 大跨拱桥实测温度和位移数据分析表明，温度作用下的位移响应具有显著的时滞效应，主梁竖向位移随着主拱、吊索和主梁有效温度的升高而增大且构件有效温度与主梁竖向位移具有明显的非线性关系，构件间温差和主拱温度梯度与主梁竖向位移呈线性相关性。

(2) LSTM 神经网络模型可以准确描述多元温度与位移的非线性映射关系，主拱有效温度和主梁与主拱之间的温差是影响大跨拱桥主梁竖向位移的主要温度变量。

(3) LSTM 神经网络能够捕捉时序数据中的长期依赖关系，可以基于温度的当前和先前信息预测当前的竖向位移。自适应矩估计方法和丢弃正则化技术能够显著提升温度-位移神经网络模型的预测精度。与BP 神经网络模型相比，LSTM 神经网络模型具有更高的重构精度和更低的预测误差。

本文仅给出了多个温度变量输入、一个温度位移输出的LSTM 神经网络模型建立方法。对于多个温度变量输入、多个温度位移输出的LSTM神经网络模型的构建，其网络结构和参数的选择，还需要进一步研究。