基于Pearson相关系数的集输管道流动腐蚀主控因素分析

宫彦双 谷坛 安超 张爱良 廖柯熹

1.中国石油塔里木油田分公司油气工程研究院2.中国石油天然气股份有限公司规划总院 3.西南石油大学石油与天然气工程学院

天然气管道在输送过程中受管道周围环境影响而发生变化,如管道沿线地形起伏变化、管道外温度、压力变化、腐蚀、自然灾害、第三方破坏、管材缺陷等因素会严重影响管道的正常运行[1-2]。尤其对于集输气管道特别容易出现腐蚀问题[3-4],腐蚀会对管道的安全运行产生巨大威胁,造成难以估量的损失。由于油气介质具有易燃、易爆等特性,所以集输管道发生事故产生的危害会更严重[5]。专家学者统计表明,腐蚀是造成管道失效的主要因素[6-8]。集输管道内部气体成分复杂,水含量、流速等都可能导致腐蚀现象发生[9-12]。因此,确定影响管道腐蚀的主控因素是一个重要的课题。

根据油气田集输管道的特点,建立管道多相流计算模型,确定不同节点流动参数的变化规律。采用Pearson相关系数,分析腐蚀速率与因素之间的相关性,确定影响集输管道的主控因素。

1 多相流计算模型

目前,许多学者对气液两相管流机理模型方面进行了相关研究,取得了一定的成果。如在接近水平管的水力计算模型方面,Xiao等提出了针对性的解决方法[13-14]。在直井和斜井水力计算模型方面,Kaya等提出了对应的计算方法[15]。王盼峰等[16]通过分析,提出了适用于海底多相流管道内腐蚀速率预测的PCAPSO-SVM 模型,通过40多组数据对模型进行拟合,并且用10多组数据对拟合出的模型进行了验证,结果表明:温度对海底多相流管道内腐蚀速率的影响相对较大,压力对其的影响相对较小;使用PCA-PSOSVM 组合模型对海底多相流管道内腐蚀速率预测的平均绝对误差仅为1.848%,模型训练时间仅为3.17 s,这两项数据均小于其他预测模型,由此可看出,PCA-PSO-SVM 组合模型对于海底多相流管道的腐蚀预测具有很好的效果。夏婧等[17]以流体的基础数据,根据SH/T 3035-2007《石油化工工艺装置管径选择导则》中两相流型的计算模型,设计了一个适用于石化装置牛顿性流体的管道两相流流型判断及管径计算软件。然而,这些模型都存在以下两方面的问题:

(1)流型转化模型和水动力模型之间的分离。

(2)模型是为不同流型、倾斜角度、流量或持液率等气体参数而建立。

对此,Zhang等通过大量的研究,建立了从水平到所有倾斜角度的流型转变、压力梯度、持液率和段塞特征的通用气液两相水力学模型[18]。

1.1 水动力模型

针对段塞流的工况,可以构建连续性方程和动量方程。

(1)连续性方程。对于充分发展的段塞流,流入和流出液膜区控制体的质量流量应该相等,据此推导出连续性方程:

同理,可列出气相的连续性方程:

将式(1)和式(2)相加可得:

针对段塞流的单元体,有如下的等量关系:

段塞长度满足以下关系:

泰勒气泡中关于液体夹带率的计算如式(7)所示:

式中:ρl为液体密度,kg/m3;A为控制体截面积,m2;Hls为液弹持液率,无量纲;Hlf为液膜持液率,无量纲;HlT为泰勒气泡持液率,无量纲;ws为液弹气液混合物速度,m/s;wT为泰勒气泡速度,m/s;wf为液膜区速度,m/s;wt为液体段塞前速度,m/s;wsl为液相的速度,m/s;wsg为气相的速度,m/s;Lu为段塞单元长度,m;Ls为液弹区长度,m;Lf为液膜区长度,m。

(2)动量方程。动量方程的控制体为液膜。在段塞流的充分发展阶段,控制体的受力应该处于平衡状态。因此,液膜动量方程如式(8)所示:

同理,气泡的动量方程如式(9)所示:

式中:p2为泰勒气泡的上游压力,Pa;p1为泰勒气泡的下游压力,Pa;ρT为泰勒气泡密度,kg/m3;τl为液膜与管壁间剪切应力,Pa;τf为气液界面剪切应力,Pa;τT为泰勒气泡与管壁间剪切应力,Pa;Sl为液相与管壁之间的湿周,m;Sf为气液相间湿周,m;ST为泰勒气泡与管壁间的湿周,m;g为重力加速度,取值9.8 m/s2;ρg 为气泡密度,kg/m3;θ为管流控制体倾角,rad。

泰勒气泡的密度定义为:

联立式(8)、式(9)、式(10),可得计算压降的动量方程:

对于分层流的动量方程,可由段塞流的方程转化得到,其方程为:

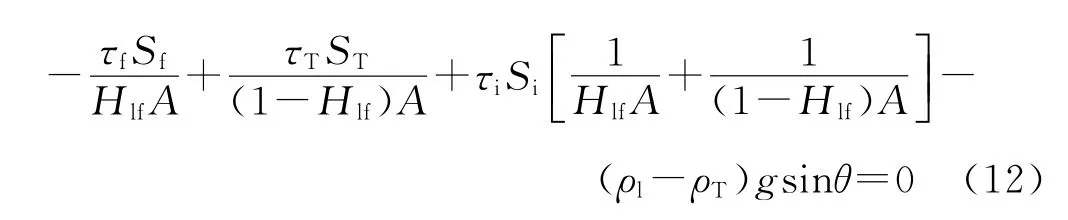
环状流的处理方法类似,但其特殊之处在于环状流的气泡和管壁相互隔离,所以,环状流的动量方程如式(13)所示:

对于分层流或环状流,其液相和气相的表观速度计算式如下:

气泡流包括分散气泡流和泡状流。计算分散气泡流的持液率和压力梯度是基于气液相混合均匀。对于泡状流,必须考虑相对于液体的气泡上升速度。

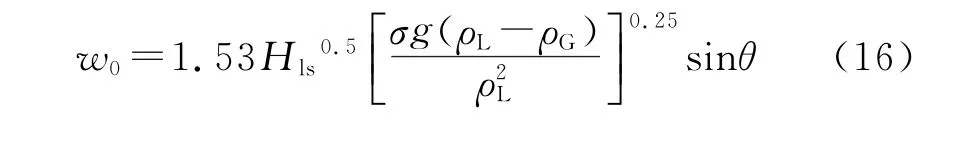
为了更好地求解,采用Zhang-Sarica水力学模型,具体求解过程如图1所示[18]。

1.2 OLGA计算模型

目前,国内外对于多相流的分析常用OLGA 软件进行处理,该软件由挪威的ScandPower(SPT)公司开发,在多相流分析中得到了广泛的应用与验证。OLGA软件可以模拟多相流的运动状态,并且对于油气管道的流动保障问题有很好的实践效果。

OLGA 软件的模型中除了包括气相和液相外,还包括一个液滴场,是一个扩展的双流体模型,物理模型为:

(1)气体、边界层液体、液滴的连续性方程。

气液两相流连续性方程:

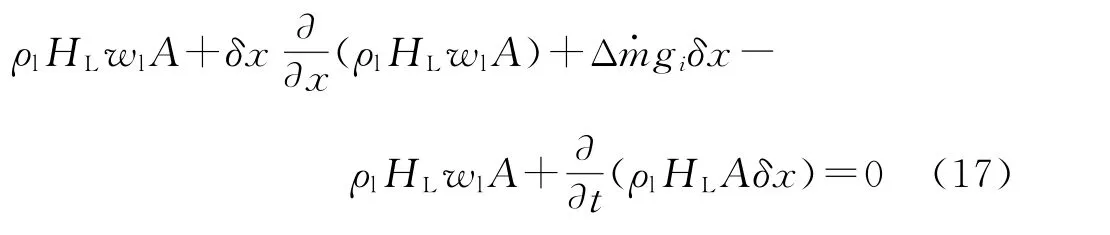
液相:

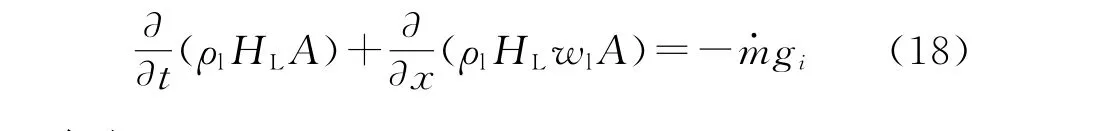
气相:

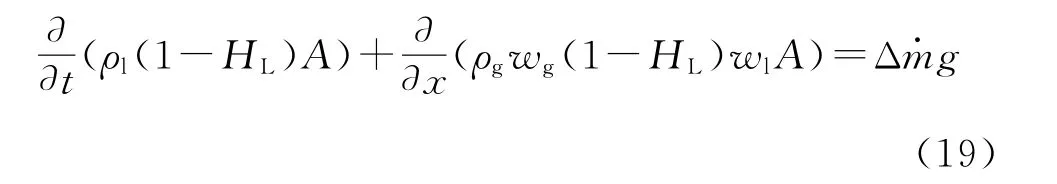
气液相混合:

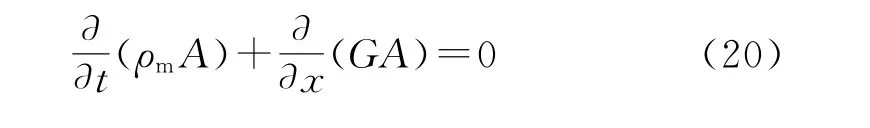
(2)两个动量方程。两个动量方程分别是气相和液相的动量方程。

液相:

气相:

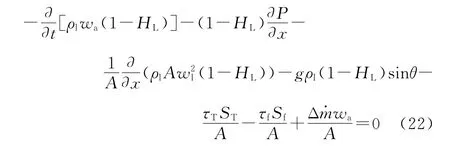
(3)混合的能量方程:

式中:ρl 为液体密度,kg/m3;ρg为气泡密度,kg/m3;ρm为气液混合物密度,kg/m3;A为控制体截面积,m2;Hl为持液率,无量纲;wt为液体速度,m/s;wg为气体速度,m/s;wa为混合物速度,m/s;t为时间,s;Δm为质量变化率,kg/s;G为通过单位面积的质量流量,kg/(s·m2);p为压力,Pa;y为质量含气率,无量纲。

通过3个连续性方程的运算,可以得到相应的压力方程。同时,相对压力和相对速度可以由压力方程和动量方程一起联立求得。

2 Pearson相关系数

Pearson Correlation Coefficient(PCC)方法是一种统计学方法,可以定量地衡量变量之间的相关关系[19-20]。PCC是一种准确度量两个变量之间的关系密切程度的统计学的方法。通过多相流模拟可以得到若干组数据,记为(x i,y i)(i=1,2,…,n)其表达式为[21]:

式中:r为相关系数值;x i为变量x对应的不同数值为变量x的平均数;y i为变量y对应的不同数值;为变量y的平均数;n为变量个数。

相关系数的取值范围介于-1～1之间。其具体判断见表1。

表1 相关系数取值表[22-24]

由于通过样本数据计算相关系数r,数值受到样本抽取的随机性和样本数量的影响。因此,需要进行样本相关系数的可靠性验证。首先,假设H0是与样本无关的估计。其次,计算检验的统计量,通常情况下采用t分布检验,其表达式为:

最后,根据给定的显著性水平α和自由度d f=n-2,利用t分布表查出tα/2(n-2)的临界值。若|r|＞tα/2|r|,则拒绝原假设H0,表明总体两个变量之间存在显著的线性关系。

文中主要关注于相关性分析,可以通过式(25)而不是相对明显的水平α来计算统计量,并通过t分布表获得满足拒绝H0的α值。PCC方法已经在社会学科、医疗学科、机电学科等领域进行广泛的运用,借鉴此方法分析集输管道腐蚀速率与介质组分和流动因素之间的相关性,确定影响集输管道的主控因素。

3 目标管道多相流动参数主控分析

3.1 多相流参数的计算

目标管道全长43.4 km,内径219.1 mm,壁厚8.8 mm,材质为L360NB,于2001年开始投产。管道的里程-高程见图2,气质组分见表2。

国内外石油集输管道均采用专业的OLGA 多相流瞬态仿真模拟软件,建立管道的里程-高程模型,按照内腐蚀直接评价标准,将管道按照≤50 m 为标准,将目标管道划分为12444个节点。以管道进出口压力温度与实际相符为原则,通过对实际生产状况的模拟,得出每条管道不同工况下的沿程温度、压力、流型流态、持液率、壁面剪切力、气液相流速等流动参数。

表2 目标管道天然气组成 y/%

温度:从起点到终点,温度从30.00 ℃变化到18.62 ℃,每千米温降0.26 ℃。压力:从起点到终点,压力从2.94 MPa 变化到1.55 MPa,每千米压降0.032 MPa。壁面剪切力:从起点到终点,气体壁面剪切力从1.09 Pa上升到2.03 Pa。液体壁面剪切力从1.43 Pa上升到4.37 Pa。流速:从起点到终点,气体流速从4.74 m/s上升到8.77 m/s。液体流速从0.19 m/s上升到0.31 m/s。持液率:从起点到终点持液率从0.0007下降到0.0006。

通过模拟,目标管道运行稳定后沿线温度、压力、壁面剪切力、持液率、气液相流速的变化见图3。随着里程的增加,温度、压力和持液率呈现降低的趋势,气液壁面剪切力和气液流速呈现逐渐升高的趋势。

根据高程测绘数据和流场分析数据,选取12处开挖点进行开挖直接检测。开挖直接检测采用的检测方式为超声波测厚,检测结果见表3。检测结果表明,目标管道抽检部位壁厚为7.58～9.85 mm。

表3 开挖直接检测结果统计表

根据超声波测厚结果,确定了目标管道的腐蚀速率。根据目标管道的特点,将管道分为两段,得到每段管道的温度、压力、流型、壁面剪切力、流速和持液率的平均值与内检测缺陷腐蚀速率的关系,温度、压力、壁面剪切力、流速和持液率与腐蚀速率均相关(见表4)。

3.2 主控因素的分析

针对目标管道的多相流模拟结果和超声波测厚结果,共取12个数据点,当CO2含量约为2.826%(摩尔分数),腐蚀速率在0.007～0.064 mm/a范围内时,采用Pearson相关系数法分析集输管道腐蚀速率与温度、压力、壁面剪切力、流速和持液率等因素的相关性,确定影响集输管道腐蚀的主控因素。

根据Pearson相关系数以及多相流模拟计算温度的结果,流动参数与腐蚀速率的相关系数见表5。温度、压力、气体壁面剪切力、液体壁面剪切力、气体流速、液体流速、持液率与腐蚀速率的相关系数都大于0.4,说明它们之间有相关关系。

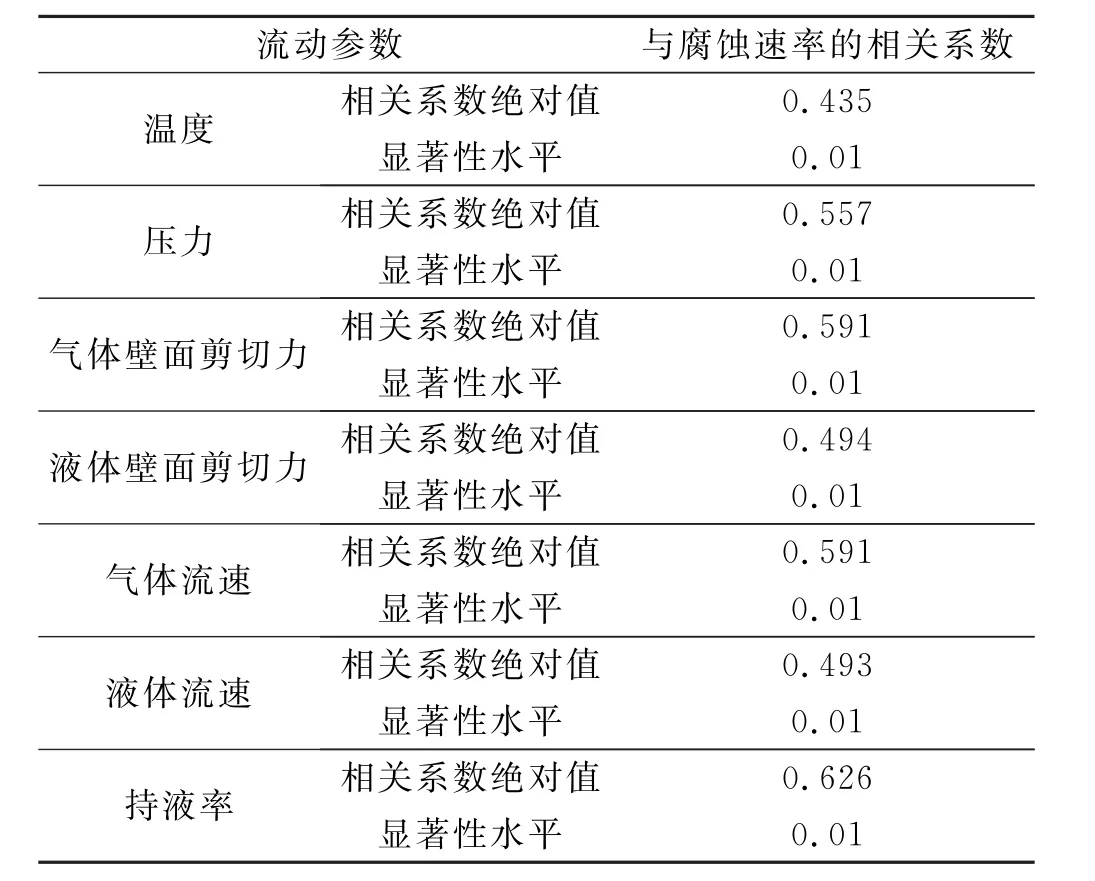
表5 目标管道流动参数与腐蚀速率的相关系数绝对值

流动参数与腐蚀速率的关联度分析如图4所示。管道的温度、压力和持液率与腐蚀速率规律呈现正相关,但壁面剪切力和流速的整体规律与腐蚀规律呈现负相关。

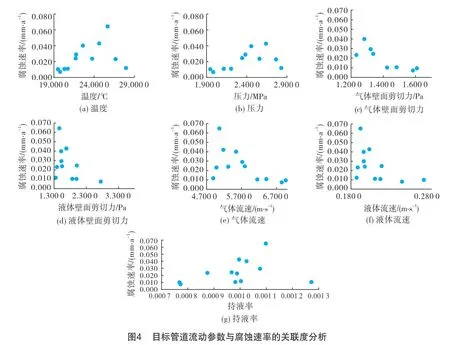
通过PCC分析得到集输管道中腐蚀速率与温度、压力、壁面剪切力、流速持液率等因素的相关性排序为:持液率(0.626)＞气体流速(0.591)=气体壁面剪切力(0.591)＞压力(0.557)＞液体壁面剪切力(0.494)＞液体流速(0.493)＞温度(0.435)。由此可知,影响集输管道腐蚀主要的因素是持液率,其次是气体流速。

4 结论

通过建立目标管道的OLGA 模型,模拟计算得到集输管道的流动参数,采用Pearson相关系数方法分析影响腐蚀的主控因素,得到以下结论:

(1)随着里程的增加,温度、压力和持液率呈现降低的趋势,气液壁面剪切力和气液流速呈现逐渐升高的趋势。

(2)管道的温度、压力和持液率与腐蚀速率规律呈现正相关,但壁面剪切力和流速的整体规律与腐蚀规律呈现负相关。

(3)影响集输管道腐蚀主要的因素是持液率(0.626),其次是气体流速(0.591)。