关于路的k-方图的邻点可区别-边全染色和第一类弱全染色

严谦泰

(安阳师范学院 数学与统计学院，河南 安阳 455000)

1 研究背景

图的染色问题具有重要的实际意义和理论意义。由计算机科学和信息科学等所产生的一般点可区别边染色[1]、邻点可区别边染色[2-6]、邻点可区别全染色[5]等都是十分困难的问题。在此基础上，张忠辅等人提出了邻点可区别-边全染色[6]和第一类弱全染色的概念，并得到一些重要的结论。本文给出了路的k-方图的邻点可区别-边全染色数和第一类弱全染色数。

定义1[3]图G(V，E)的一个正常全染色f:V∪E→{1,2,…,k}，如果满足：

1)对任意的uv∈E有f(u)≠f(v),f(u)≠f(uv),f(v)≠f(uv)

2)对任意的uv,vw∈E有f(uv)≠f(vw)，且C(u)≠C(v)

则称f是图G(V,E)的一个邻点可区别全染色，简记为k-AVDTC。在k-AVDTC中最小的数k称为图G(V,E)的一个邻点可区别全染色数，记为χat(G)=min{k|k-AVDTC}。

定义2[6]对于简单图G(V，E)，若映射f:

V∪G→{1,2,…,k}满足：

1)对任意的uv∈E有f(u)≠f(v),f(u)≠f(uv),f(v)≠f(uv)

2)对任意的uv∈E有C(u)≠C(v)

则称f是图G(V,E)的一个邻点可区别-边全染色，简记为k-AVD-ETC，且称

为G的邻点可区别-边全染色数，其中色集合C(u)={f(u)}∪{f(uv)|uv∈E(G)}。

定义3[7]设G=(V,E)是阶至少为2的连通图。 映射f:V(G)∪E(G)→{1,2,…,k}，k是正整数。如果f满足：

1)对任何uv∈E(G)有f(u)≠f(v)

2)对任何uv∈E(G)，vw∈E(G)，u≠v，有f(uv)≠f(vw)

则称f为G的第一类弱全染色，简记为FWTC，记χfwt(G)=min{k|k-FWTC}为G的第一类弱全染色数。

定义4 对于简单图G=(V,E),定义G的k-方图Gk如下:

V(Gk)=V(G)

E(Gk)=E(G)∪{uv|d(u,v)=k，u,v∈V(G)}

其中k是一个大于1的正整数,d(u,v)表示u和v之间的距离。

2 主要结论

引理2[6]对任意的简单图G有

引理3[6]对于n阶圈Cn有

引理4[7]对任意的简单图G有，χfwt(G)≥max{χ′(G),χ(G)}

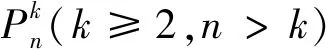
f(vi)=1,i≡1(mod 2)

f(vi)=2,i≡0(mod 2)

f(vivi+1)=3,i=1,2,…,n-1

f(vivi+k)=3,i=1,2,…,n-k

情形2.1 当k≡1,2(mod 3)时，

f(vi)=1,i≡1(mod 3)

f(vi)=2,i≡2(mod 3)

f(vi)=3,i≡0(mod 3)

f(vivi+1)=4,i=1,2,…,n-1

f(vivi+k)=4,i=1,2,…,n-k

情形2.2 当k≡0(mod 3)时，将顶点分段，每段中有k+1个顶点，即{v1,v2,…,vk+1}，{vk+2,vk+3,…,v2(k+1)}，…，每段中顶点如下染色：用1，2，3循环染色，最后一个顶点染色2，例如{v1,v2,…,vk+1}中的顶点v1,v2,…,vk用1，2，3循环染色，最后vk+1染色2。所有的边均染色4。

综上可知，

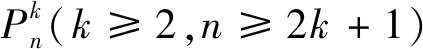
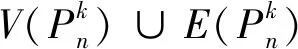
f(vi)=1,i≡1(mod 2)

f(vi)=2,i≡0(mod 2)

f(vivi+1)=1,i≡1(mod 2)

f(vivi+1)=2,i≡0(mod 2)

f(vivi+k)=3,i≡1(mod 2)

f(vivi+k)=4,i≡0(mod 2)

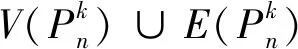
情形2.1 当k≡1,2(mod 3)时，

f(vi)=1,i≡1(mod 2)

f(vi)=2,i≡0(mod 2)

f(vivi+1)=1,i≡1(mod 2)

f(vivi+1)=2,i≡0(mod 2)

f(vivi+k)=3,i≡1(mod 2)

f(vivi+k)=4,i≡0(mod 2)

情形2.2 当k≡0(mod 3)时，将顶点分段，每段中有k+1个顶点，即{v1,v2,…,vk+1}，{vk+2,vk+3,…,v2(k+1)},…,每段中顶点如下染色：对其前k个顶点，用1，2，3循环染色，最后一个顶点染色2，例如{v1,v2,…,vk+1}中的顶点v1,v2,…,vk用1，2，3循环染色，最后vk+1染色2。

f(vivi+1)=1,i≡1(mod 2)

f(vivi+1)=2,i≡0(mod 2)

f(vivi+k)=3,i∈{tk+1,tk+2,…,tk+k}，t=0,1,2,…

f(vivi+k)=4,i∈{tk+k+1,tk+k+2,…,tk+2k}，t=0,1,2,…