高压对Gd掺杂ZnO的电子结构和磁性影响研究*

宋 永，赵晓雨

(1. 阿坝师范学院 电子信息与自动化学院，四川 汶川 623002；2. 阿坝师范学院 应用物理研究所，四川 汶川 623002)

0 引 言

ZnO是Ⅱ-Ⅵ族内最为直接的宽带隙氧化物半导体材料，在室温状态下的能隙宽度约为3.37 eV，拥有60 meV的高激子束缚能[1-2]。ZnO拥有光电、压电、透明导电、气敏等优异性能，在太阳能电池板、电脑显示器及透明导电薄膜等方面具备十分广阔的应用前景，已经成为氮化镓(GaN)元素后短波长半导体材料研究的关键目标[3-5]。

以透明导电薄膜为例，由于本征ZnO存在较多的本征点缺陷，未掺杂的ZnO薄膜通常电阻率较高，性能极不稳定[6]。稀土元素因其特有的电子层结构而拥有良好的能量转换性能，可以完成稀土离子的高效光致发光，达到1.54 μm波段的近红外发射，提升ZnO的气敏特征，达到光电改性目标[7]。

利用改变外场条件驱使材料产生结构改变，已经变成发现新结构、调控材料性能的可靠途径，其中可通过压力效应作用更改材料晶体结构，展现出不同的物理性质[8]。压力对材料的作用，从微观视角来看可理解成促进各成键原子间的化学键缩小，引发物质晶体和电子结构变化；从宏观上则呈现出相应物理化学性质的改变，并在压力作用下产生相变，得到新的优异性能[9-10]，由此本文采用高压实验，对高压下Gd掺杂ZnO的电子结构和磁性影响展开深入探究。

众所周知，高压物理的发展取决于高压实验技术的发展，而高压实验技术的应用为科学及工业界提供了一个除温度和组分以外的新维度[11]，在矿物科学、地球科学、食品、生物、制药等领域均有着广阔的应用前景。处在压力作用下，物质内部分子及原子之间的距离会产生变化，更改了物质内部电子分布及能带结构状况，宏观上影响了材料的力、热、电等物理性质。在给予的能量高于物质自身化学键能量情况下，化学键会解离构成新的化学键，导致物质产生晶体结构和电子结构相变，组成拥有特殊性质的新材料[12]。由此看出，高压实验技术已成为一种研究物质在高压作用下结构平稳性和物质新规律的有效方法。

本文基于高压实验技术[13]，把高纯ZnO当作原料，将Gd掺杂进ZnO中，通过固相反应法获得试样，在高压处理下完成实验，并运用密度泛函理论下的第一性原理计算方法，了解Gd掺杂后分子实时变化情况，得到准确的高压下稀土ZnO电子结构与磁性变化情况。

1 实 验

1.1 高压基础制备

高压基础制备是成功完成实验流程的根基。本文计算的基本思路是在密度泛函理论(density functional theory，DFT)第一性原理前提下展开的，并使用Materials Studio4.4软件包内的CASTEP运算程序。在倒易K空间内，平面波终止能量为300 eV。系统能量总和与电荷密度在Brillouin区的积分计算采用Monkhorst-Pack模式，网格点大小是5×5×5，以保障体系能量与构型的收敛。

1.2 实验设备

金刚石对顶砧压机(diamond anvil cell，DAC)是现代高压实验技术内最为关键的设备之一，其根本原理为使用两个金刚石的砧面对样品腔实施挤压，让样品腔内生成高压。本文使用改进型对称式DAC高压装备，其机身厚重、强度高、导向面积大、平行度高，可运用在超高压力实验中，是现阶段最为常用的金刚石对顶砧压机高压设施。原理为利用旋拧两组对称左右旋转螺丝，凭借旋转螺丝挤压弹簧垫片令垫片生成张力，让固定于压机的活塞与圆筒内的两块金刚石互相挤压，生成高压。

1.3 实验方法

首先，在两个金刚石对应的砧面中间放置一块圆形密封垫片，材质为T301钢片；其次，拧动旋转螺丝，密封垫片受压时，在金刚石周边生成环形山状突起，可对金刚石侧面产生支撑作用；接着，在密封垫片直径为60～90 μm的大小孔隙内放入实验样品和传压介质，让压腔中维持稳定持续的静水压力；最后，增大压力，在高压处理下完成实验。

具体实验方法如下：将高纯ZnO作为原材料，并将重稀土Gd掺杂进ZnO中，通过充足研磨与混合后，利用固相反应法获得实验所需样品，再将样品通过高压处理，压力实验在金刚石对顶砧压机上进行，两面顶是利用两个同样的压砧同时挤压正方体合成块实现高压效果，具备液压系统稳定，保压性能良好等优势。把样品依次加压至3，6，9和12 GPa，保压15 min，通过高压处理后的样品色泽显著变深，硬度也随之增强。

2 基于密度泛函理论的第一性原理计算

为便于了解高压下Gd掺杂ZnO内部分子的变化，使用基于密度泛函理论的第一性原理计算定义原子核与电子间的作用，平衡计算速率与精度间的矛盾，该方法在材料性质、结构评估等方面取得巨大成功[14-15]。本文将此计算方法融入高压对Gd掺杂ZnO的结构变化中，计算过程如下。

明确密度函数理论时，首先要了解物质变分原理[16]。可以将变分原理当作一个趋近于求解薛定谔方程的初始点，从试探波函数φt获得的体系哈密顿预期值总是高于或等于体系基态能量ε0，且ε0可以利用体系基态波函数φ0计算体系哈密顿预期值进行求解，得到

(1)

对随机正交归一的试探波函数而言，体系哈密顿预期值为

(2)

体系波函数φn为体系哈密顿完备的本征函数，因此试探波函数可运用波函数进行拓展

(3)

(4)

密度泛函理论基础概念是认定原子、分子及固体等基态物理性能可采用电子密度进行定义[17-18]，总结为如下定理：不计自旋的全同费密子系统基态能量为粒子数密度函数ρ(r)的唯一泛函；能量泛函E(ρ)在粒子数固定条件下对正确的粒子数密度泛函ρ(r)取极小值，且与基态能量相同。

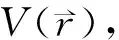
(5)

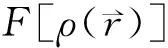
(6)

(7)

(8)

(9)

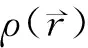
(10)

式中，

(11)

(12)

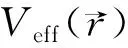
(13)

式(10)的关键点在于，使用无互相作用的电子系统动能替换有互相作用的粒子系统动能，把由互相作用的电子系统所有其余作用统一归结于交换关联互相作用泛函Exc[ρ]。和Hartree-Fock方程对比[19]，密度泛函推导出的单电子方程是严谨的，在考虑交换互相作用的同时，也纳入了关联互相作用理念。

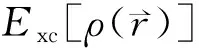
(14)

若固体内的电子不被约束在单个原子内，而是在全部固体中运动，进行此种运动的电子被叫作公有化电子，Bloch定理提供了周期势场内运动的公有化电子波函数形态[22]，记作

(15)

(16)

(17)

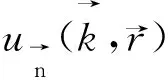
能带运算中，假如使用全电子态来求解，运算量较多，且不易收敛[23]。一般情况下，运算中较为重要的点为固体内的价电子。原子组合成固体过程中，化学环境的改变对价电子形态有着较大改变。为降低运算量，研究人员设计出赝势理念，也就是将实际的离子库仑吸引势中添加一个短程虚拟排斥势，两项总和就是赝势[24]。

赝势在原子核周边会变得比较平坦，即便赝势是人为组建的，但利用赝势运算获得的本征能量与价电子波函数和实际值是相等的，具体如图1所示。

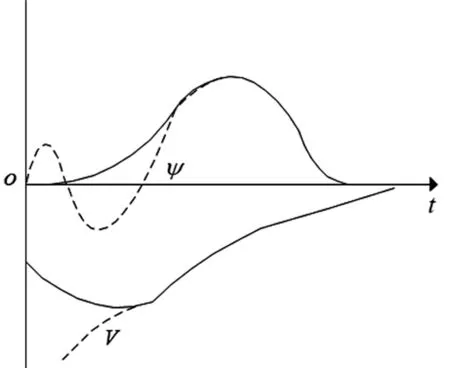
图1 赝势原理图Fig 1 Pseudo potential principle diagram

从图1可以看出，ψ为赝电子波函数正交项趋向，V为真实势能项。波函数正交项趋向于抵消真实势能项，从而给出一个有效势，比真实的晶体势弱很多，即称为赝势。由于赝电子波函数在整局空间内的改变速率较慢，所以可使用较少的平面波近似拓展，有效降低运算时间，提升ZnO分子动态演算速率。

3 结果与讨论

3.1 高压对Gd掺杂ZnO电子结构的影响分析

图2为加入Gd含量为3%(质量分数)的ZnO依次在常压、3，6和9 GPa下的XRD衍射图。从图2可以看出，伴随压强不断上升，ZnO衍射峰逐步向高衍射角转移，并且试样的每个峰值均为下降趋势。但从常压改变成压力为3 GPa的过程中，每个衍射峰反而往低衍射角移动，晶面之间的距离也是最高的，同时有新的衍射峰存在(图内方块点位置)。在仪器检测灵敏度范围中，没有出现Gd衍射峰，由此认定在掺杂含量较少时，加入的Gd占据ZnO的Zn位或者缝隙位。这是因为在合适压力下，为让Gd元素更为充分地掺杂进ZnO内，Gd元素的掺杂会引发衍射峰向小角度方位转移。Zn离子半径低于Gd离子半径，Gd原子替代Zn原子位置会引发晶格微小改变，晶格膨胀导致晶面间距变大，通过布拉格定律可以看出，半衍射角θ会逐渐变小。但在高压情况下，ZnO材料有显著的压致晶粒碎化反应，导致材料晶面间距在一定范围中减少，θ随之变大。在压强<3 GPa状态下，此种碎化反应依旧不能抵挡Gd原子引发的晶格膨胀，所以在3 GPa高压下，试样衍射峰依然会往低角方向转移。但在压强>3 GPa时，晶粒碎化反应更为显著，致使每个波谱的衍射峰往高衍射角转移。

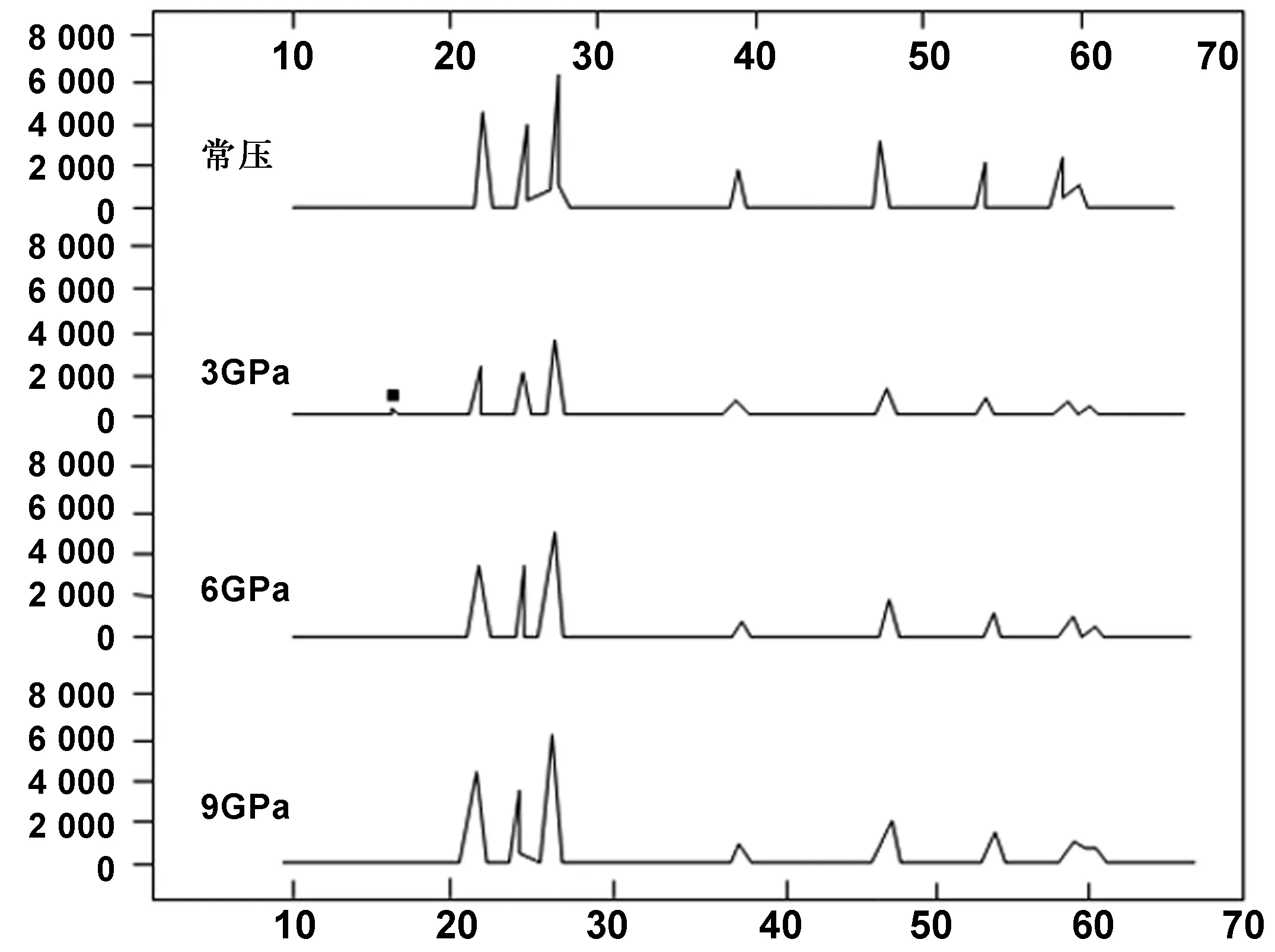
图2 Gd掺杂ZnO在不同压力下的XRD衍射示意图Fig 2 XRD patterns of Gd doped ZnO under different pressures

3.2 高压对Gd掺杂ZnO磁性影响分析

A. A. Dakhel等[25]研究发现，比较不同Gd掺杂浓度的ZnO样品磁性强度与对外加磁场的依赖关联可知，在Gd掺杂ZnO系列试样中，掺杂浓度较少(﹤3%(质量分数))的试样会出现较为显著的铁磁性；掺杂浓度较高(>3%(质量分数))的试样中即便有很多Gd磁性离子，并在低温中也有相当数量的铁磁有序，可在常温下Gd磁性离子没有构成长程铁磁有序。对以上现象的解释为：空穴浓度的增多能够让试样获得较高的居里温度。在居里温度运算模型内，在磁性离子浓度较少时，一般能够省略反铁磁性互换作用对居里温度的影响[26]。反铁磁性互换作用对居里温度的影响和磁性离子浓度及空穴浓度的比值有紧密关联，空穴浓度较少情况下，反铁磁性互换作用对居里温度有明显的影响。合理增添空穴浓度，降低磁性离子和空穴浓度比值，可有效提升居里温度。本文选取Gd含量为3%(质量分数)的ZnO掺杂样品，依次在15和400 K下测验试样的磁化强度和外加磁场间的耦合惯量。

图3为Gd含量为3%(质量分数)的ZnO掺杂试样分别在常压、4和7 GPa压力处理后，在T=15 K下的磁滞回线。由图3可知，在T=15 K下，试样磁化强度伴随不同的高压模式产生明显变化。处于低温区时磁化强度M最高达到0.055 Am2/kg，并拥有磁滞回线，说明试样为铁磁有序。从图3还可以看出，通过4 GPa高压的试样磁化率要高于常压下的试样，通过7 GPa高压的试样磁化率低于常压下的试样。

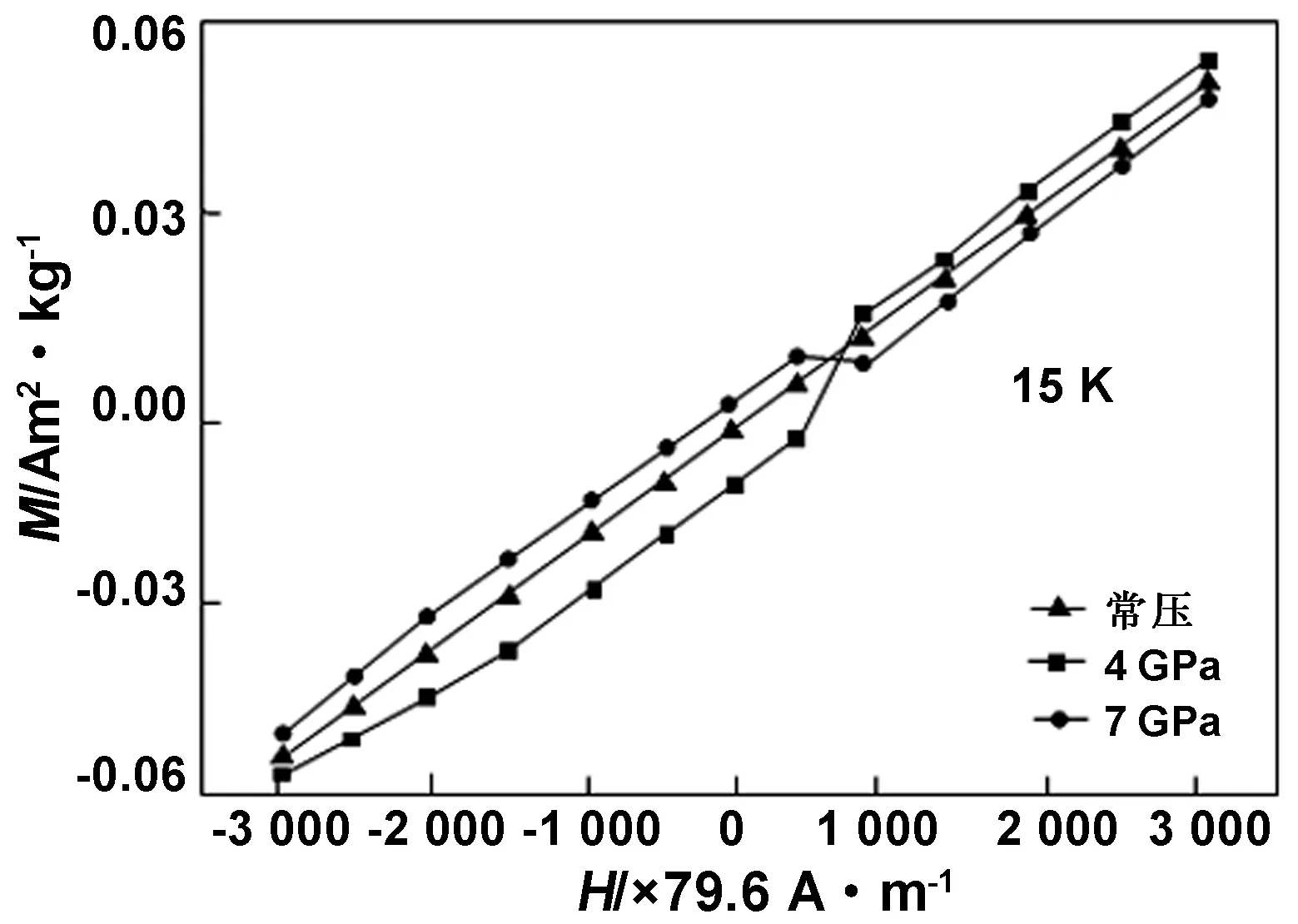
图3 Gd掺杂ZnO试样在不同压力及T=15 K下的磁滞回线Fig 3 Hysteresis loops of Gd doped ZnO under different pressures and T = 15 K

图4为Gd含量为3%(质量分数)的ZnO掺杂试样分别在常压、4和7 GPa压力处理后，在T=400 K下的磁滞回线。从图4可以看出，在T=400 K的情况下，试样的磁化强度M均高于0，所以可以断定试样的居里温度高于室温。对比图3和4，试样的磁滞回线具有显著改变，但试样的磁性能变化具有部分相似性。由图4可知，通过4 GPa高压处理试样的M值要高于其余两种试样，3类试样的磁化率大小依次为4 GPa处理试样大于常压处理试样大于7 GPa处理试样。3类试样的矫顽力与剩余磁化强度均不相同，4 GPa处理下的试样拥有最高剩磁，7 GPa处理下的试样矫顽力最高。

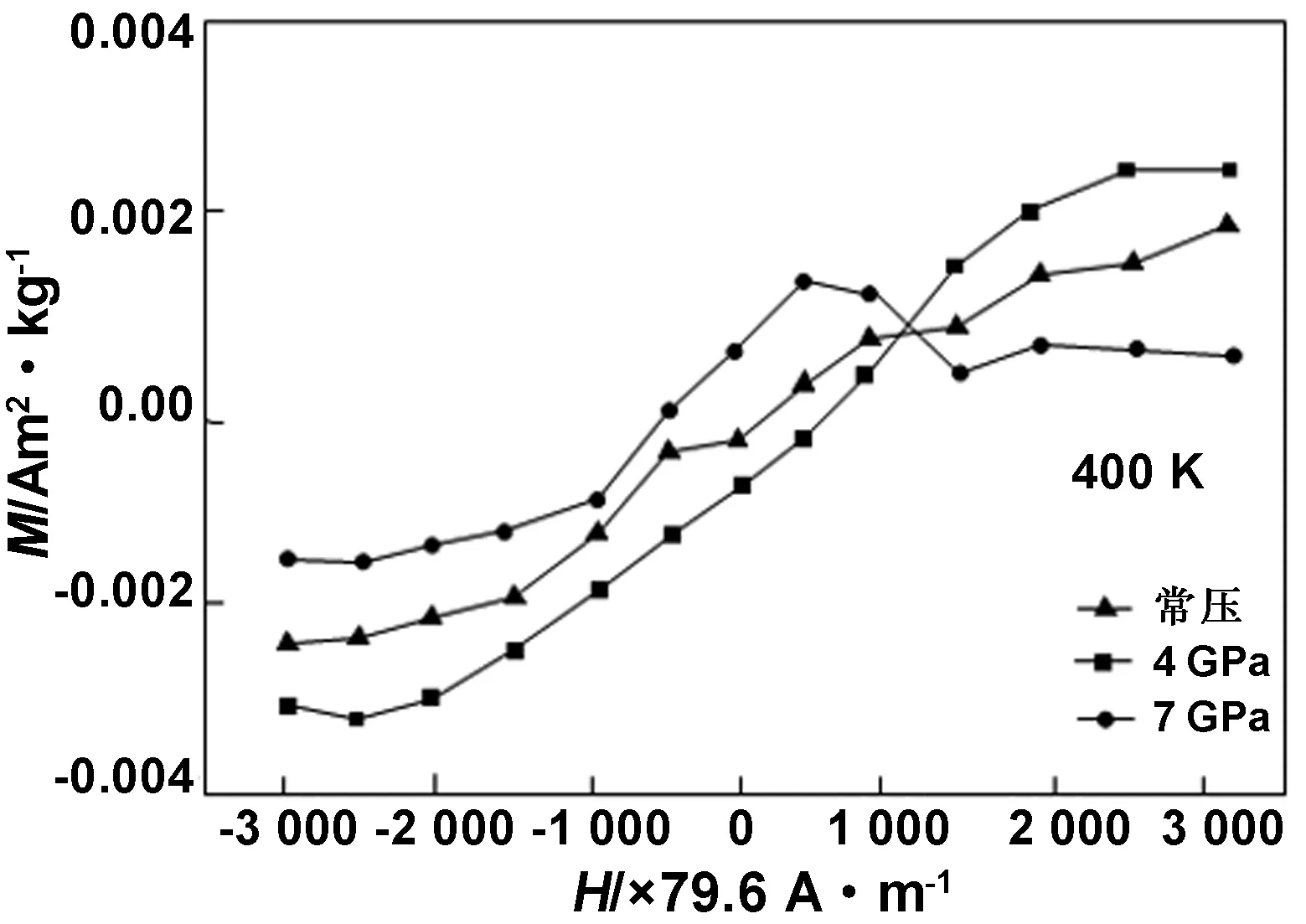
图4 Gd掺杂ZnO试样在不同压力及T=15 K下的磁滞回线Fig 4 Hysteresis loops of Gd doped ZnO under different pressures and T = 400 K

由图3和4分析可知，Gd含量为3%(质量分数)的ZnO掺杂样品通过不同高压处理后在T=15和400 K下的电子结构及磁化强度发生明显改变，原因可能是Gd掺杂进ZnO试样后，随压强持续增大，ZnO衍射峰会向高衍射角转移，且试样每个峰值均呈现下降趋势，电子结构发生明显变化；不同高压对试样的铁磁性产生影响，4 GPa高压处理试样能很好地增强材料的磁性能，让其饱和磁化强度与磁化率得到显著提升；但7 GPa高压处理试样会对材料磁性产生不良影响，让材料的各项磁性能反不如常压下的试样。由此可知，利用高压方式能够在一定标准下促使Gd元素在ZnO内的掺杂溶解，可过度压力也会影响试样内的空穴浓度，因此需要精准把握高压强度，让其对ZnO全局性能的提升产生积极作用。

4 结 论

使用金刚石对顶砧压机和Materials Studio4.4软件包中的CASTEP运算程序，并融合密度泛函理论下第一性原理计算方法，对高压下Gd掺杂ZnO试样的电子结构与磁性影响进行深入研究。得出如下结论：

(1)基于密度泛函理论的Gd掺杂ZnO试样的第一性原理计算中，利用赝势运算获得的本征能量与价电子波函数和实际值是相等的，由于赝电子波函数在整局空间内的改变速率较慢，所以可使用较少的平面波近似拓展，有效降低运算时间，提升ZnO分子动态演算速率。

(2)XRD分析可知，Gd掺杂进ZnO试样后，Gd占据ZnO的Zn位或者缝隙位，随压强持续增大，ZnO衍射峰会向高衍射角转移，且试样每个峰值均呈现下降趋势，在压强>3 GPa时，Gd掺杂ZnO试样的电子结构生成晶粒碎化显著，致使每个波谱的衍射峰往高衍射角转移。

(3)不同高压对Gd掺杂ZnO试样的铁磁性产生影响，4 GPa高压处理试样能很好地增强材料的磁性能，让其饱和磁化强度与磁化率得到显著提升；但7 GPa高压处理试样会对材料磁性产生不良影响，让材料的各项磁性能反不如常压下的试样。因此适当高压处理可增强材料的铁磁性，但压力超出一定值后，材料磁性能出现下降。