层数对二维SnS的晶体结构及电子结构的调控
孙 梦, 武晓倩, 刘亭亭, 苏宁宁
(中北大学 理学院, 山西 太原 030051)
0 引言
SnS是典型的层状半导体材料,由于具有较高的热电优值[1]和较大的光吸收系数以及环保、无毒且地球储量丰富[2,3]等优点在半导体探测器[4]、光伏器件和热电器件[5,6]等领域具有广阔的应用前景.常压下,稳定的SnS具有正交结构(Pnma).
近年来,随着石墨烯通过机械剥离的方法从母体中直接分离出来,并且展现出异于体材料的热学、光学和电学等性质[7-9],二维SnS便激起了很多理论和实验工作者的研究兴趣.理论上,Fei和Wu等[10-12]通过第一性原理计算分别提出了二维单硫系化合物特有的巨大压电效应和强大的平面内铁电性;Li等[13]通过第一性原理计算,提出杂化层间耦合可以优化二维SnS的电子及电热性能;Tritsaris等[14]通过第一性原理计算提出SnS的光学性质及能带结构对层数有一定的依赖性.
实验上,Sarkar等[15]通过液相剥离法制备了超薄的SnS,发现其具有更高的温度敏感性和良好的非线性光学特性;Brent等[3]通过液相剥离法制备了单层到几层的SnS,并通过光吸收实验观察到带隙对层数具有很强的依赖性;Tian等[16]通过物理气相沉积法合成了厚度约6 nm(~10层)的SnS纳米片,发现此纳米片具有Pnma结构,且面内存在很强的异向性;Zhang等[17]用单源前体法合成出了厚度约20 nm的SnS纳米片,发现此纳米片是pbnm的正交结构.
可见,有别于物理机械剥离方法,当采用化学合成时,由于各结构的形成能不同,二维的SnS会呈现出不同于体材料的晶体结构.而物质的结构对性质具有决定作用,那么当SnS的厚度减少到极少层时,合成的SnS将具有怎样的晶体结构和电子结构将直接决定少层SnS的热学、光学和电学等性质.
Crystal Structure Analysis by Particle Swarm Optimization (CALYPSO)是一种基于粒子群优化算法的晶体结构预测程序[18-22],在二维层状材料的结构预测上已经取得了很多成果.如Gao等[23]通过CALYPSO软件成功预测出了氢化石墨烯以及氧化石墨烯的最佳结构;Zhang等[24]通过CALYPSO软件结合密度泛函理论对二维化合物Bx/2Nx/2C1-x(0 据此,本文将通过CALYPSO软件,对块体SnS晶体及纳米单层、双层和三层SnS进行结构搜索,并通过Vienna Ab-initio Simulation Package (VASP)软件对预测出的结构进行结构优化和电子结构性质的计算,进而分析层数对二维SnS的晶体结构和电子结构的调控性.本文的研究将对极少层SnS的合成以及少层SnS在太阳能电池和热电领域的应用提供理论指导. 本文采用了基于粒子群优化算法的CALYPSO软件,对纳米单层、双层、三层和体材料SnS分别进行结构搜索.其中,对单层、双层和三层SnS晶体沿着Z轴设置了40 Å的真空层,分子式设置为单倍胞.对搜索出来的结构用VASP软件包进行结构优化,并用MedeA软件中的VASP[27]模块完成能带、态密度、电子局域密度及Bader[28]电荷转移的计算,采用广义梯度近似(GGA)[29]下Perdew-Burke-Emzerh(PBE)[30]交换关联泛函来描述结构中电子间的交换关联势能.赝势采用全电子投影缀加平面波[31]方法. Sn原子的价电子为5s25p2,S原子的价电子为3s23p4.为了计算精确,平面波的截断能选择350 eV.第一布里渊区积分采用网格间距为0.02 nm-1的Monkhorst-Pack[32]网格方法.优化过程中,在确保空间群不变的情况下,采用10-5eV为自洽能量收敛的最小值,优化的应力收敛设置为0.001 eV/Å,温度设定为0 K. 物质的稳定程度可通过吉布斯自由能的大小来判断,吉布斯自由能越小物质越稳定.由公式G=H-TS(G为吉布斯自由能,H为焓,T为温度,S为熵)可知,温度T为0 K时,可以用焓值代替系统的自由能. 本文将CALYPSO预测得到的块体SnS、纳米单层、双层及三层SnS的前五个焓值最低的结构及其相对应的焓值列于表1. 表1 CALYPSO预测出的块体SnS及少层SnS 由表1可知:常压下,空间群为Pnma的块体SnS的焓值更低,说明常压下稳定的SnS具有正交结构(Pnma),该常压结构与前人的研究相一致,这为本文成功预测纳米少层SnS的常压结构提供了保证.纳米单层、双层和三层SnS具有与体材料不同的晶体结构.单层SnS,空间群为C2/m的结构焓值更低,平均每个原子的能量为-4.3 eV;双层和三层SnS,空间群为P4mm的结构焓值更低,结构更加稳定,此状态下,平均每个原子的能量分别为-4.2 eV和-4.3 eV.单层SnS与双层和三层SnS的晶体结构并不相同,这与层间的分子间作用力有关[33].例如,前人在石墨烯的研究中也发现双层石墨烯的几何结构与单层石墨烯有很大差别[33].单层SnS具有与双层和三层SnS不同的晶体结构,说明层间的分子间作用力对晶体结构的形成具有重要作用,双层和三层SnS由于层间分子间作用力而具有相同的空间群. 图1为通过CALYPSO预测出的块体SnS、纳米单层、双层及三层的SnS的晶体结构,各相的晶格常数及原子位置列于表2. (a)、(b)、(c)和(g)分别为一层、二层、三层和块体SnS的剖面图 (d)、(e)、(f)和(h)分别为一层、二层、三层和块体SnS俯视图图1 SnS的晶体结构 SystemPhasePressure/GPaLatticeParameters AtomsWyckoffpositionXYZMonolayerC2/m0a=5.838 Å,Sn4i0.7640.0000.544b=5.831 Å,c=32.45 Å,α=90 °,S4i0.7380.0000.464β=93.62 °,γ=90 °.BilayerP4mm0a=4.934 Å,Sn11b0.5000.5000.530b=4.934 Å,Sn21a0.0000.0000.595c=37.68 Å.Sn31b0.5000.5000.422Sn41a0.0000.0000.422S12c0.5000.0000.563S22c0.5000.0000.453 续表2 SystemPhasePressure/GPaLatticeParameters AtomsWyckoffpositionXYZTrilayerP4mm0a=4.921 Å, Sn11b0.5000.5000.628b=4.921 Å,Sn21a0.0000.0000.628c=42.28 Å.Sn31b0.5000.5000.527Sn41a0.0000.0000.469Sn51b0.5000.5000.425Sn61a0.0000.0000.367S12c0.5000.0000.599S22c0.5000.0000.498S32c0.5000.0000.395BulkPnma0a=11.41 Å,Sn4c0.8790.2500.124b=4.038 Å,S4c0.1480.2500.477c=4.374 Å. 从图1可以看出,单层SnS是通过Sn-S键结合成具有上下两个相同的弯曲SnS原子层,层间距约为2.6 Å,同一层的每个Sn原子连接4个S原子,键长约为2.9 Å,键角约为89.7 °.双层SnS存在两种Sn-S原子层,层间距约为2.9 Å,上层Sn-S原子层中,每个Sn原子连接4个S原子,键长约为2.7 Å,键角约为128.4 °;下层Sn-S原子层中,每个Sn原子连接4个S原子,键长约为2.7 Å,键角约为127.1 °.三层SnS同样存在两种Sn-S原子层,其中上层与中间层的层间距约为3.1 Å,中间层与下层的层间距约为1.9 Å,上层Sn-S原子层中,每个Sn原子连接4个S原子,键长为2.7 Å,键角约127.9 °,中间层和下层的原子层Sn、S原子排布相同,每个Sn原子均与4个S原子连接,键长约为2.7 Å,键角约为126.5 °. 为了研究不同结构的SnS的能带结构及带边电子态的起源,对常压下块体SnS和少层SnS的能带结构以及电子态密度分别进行了计算.计算结果如图2和图3所示.在图2和图3中,(a)表示晶体;(b)表示一层;(c)表示二层;(d)表示三层. 由图2可以看出:常压下,块体SnS的导带底位于高对称点Γ、B之间,价带顶位于高对称点F、Γ之间,因此是间接带隙半导体材料,其带隙宽度为0.89 eV,与吴琼等[2]的计算结果相一致.双层和三层SnS的导带底均位于高对称点Γ,而单层SnS位于高对称点Z、M之间,出现这种差异的原因是因为单层SnS没有层间相互作用,导致其对称性发生了改变.双层和三层SnS的价带顶都位于高对称点F、Γ之间,单层SnS的价带顶位于高对称点Γ、Z之间,因此单层、双层和三层SnS皆为间接带隙半导体材料,且禁带宽度分别为1.35 eV、0.24 eV、0.17 eV.少层SnS的带隙对层数具有依赖性,带隙宽度会随着层数的增加而减小,此结论与Brent等[3]的光吸收实验结果相一致. (a)常压下晶体SnS的能带结构 (b)常压下一层SnS的能带结构 (c)常压下二层SnS的能带结构 (d)常压下一层SnS的能带结构图2 常压下SnS的能带结构 此外,从图2还可以看出,对少层SnS来讲,随着层数的增加,SnS的能带起伏逐渐减小,说明电子的非局域程度随层数的增加而较小,原子轨道扩展性减弱,相邻轨道之间的重叠率增大,该结果表明随着层数的增加,成键性加强.这个结果也表明层间的相互作用可以增加系统的稳定性,这与吴琼等[2]的层间相互作用可以降低系统的总能的结论相一致.因此,通过降低SnS层间的相互作用,更有利于在实验上合成单层的SnS. 结合图3中所有相的总态密度和分态密度分布可以看出,各相在离费米能级最近的价带区均是S原子的p轨道对其贡献最大,导带区均是Sn原子的p轨道对其贡献最大,表明这4个相的费米能级附近的电子态密度主要由S原子的p轨道和Sn原子的p轨道提供,同时这4个相的Sn原子、S原子的p轨道以及总态密度在费米能级附近都有剧烈下降,说明Sn原子和S原子之间存在共价键[34].另外,所有相在-15~-11 eV区间的价带区均是S原子的s轨道对电子态密度贡献最大,在-9~-4.5 eV区间的价带均是Sn原子的s轨道对电子态密度贡献最大.由此可见,层数不会影响原子轨道对电子态密度的最大贡献率. (a)常压下晶体SnS的态密度 (b)常压下一层SnS的态密度 (c)常压下二层SnS的态密度 (d)常压下三层SnS的态密度图3 常压下SnS的态密度 为了探究预测得到的层状SnS晶体结构的化学键,分别计算了这4个相的电子局域密度函数,等值面均取值0.766,其结果如图4所示.由图4可以看出:在Sn原子和S原子之间存在电子局域,并且电子局域围绕在S原子周围,说明这4个相中的Sn原子和S原子之间存在极性共价键.而且随着层数的增加,S原子周围的颜色减淡,说明电子的局域程度随层数的增加而减小,二维SnS的成键性随着其层数的增加而加强.此结果与能带结构的计算结果相一致. (a)常压下晶体SnS电子局域密度 (b)常压下一层SnS电子局域密度 (c)常压下二层SnS电子局域密度 (d)常压下三层SnS电子局域密度图4 常压下SnS电子局域密度 为了清楚地描述S原子和Sn原子之间的电荷转移情况,计算了Bader电荷转移,计算结果列于表3.S原子的电负性比Sn原子的电负性强,所以S原子吸引电子的能力强于Sn原子,Sn原子与S原子之间进行的电荷转移中,施主为Sn原子,受主为S原子,Sn原子和S原子之间的电荷积累是共价键作用.通过表3可以看出,从单层SnS到三层SnS每个Sn原子向S原子电荷的转移分别为0.96 e、0.90 e和0.59 e.因此,层数的不同会影响Sn原子向S原子转移的电荷量,并且随着层数的增加,Sn原子向S原子转移的电荷量会减小. 表3 SnS的电荷转移 本文通过CALYPSO晶体结构预测软件结合第一性原理方法,对少层SnS常压下的晶体结构和电子结构进行了系统的研究. 晶体结构的预测结果显示:常压下,单层SnS的空间群为C2/m,双层和三层SnS的空间群为P4mm.单层SnS与双层和三层SnS的晶体结构并不相同,这与层间的分子间作用力有关,说明层间的分子间作用力对晶体结构的形成具有重要作用,这为实验上单层SnS的合成提供了方向,比如通过离子插层的方式降低层间的相互作用力[35]. 能带结构计算表明:常压下,块体和少层SnS均为间接带隙半导体,且带隙宽度会随着层数的减少而增加,层数对带隙具有调控作用. 态密度计算表明:在离费米能级最近的价带区是S原子的p轨道对其贡献最大,导带区是Sn原子的p轨道对其贡献最大,并且层数的改变不会影响原子轨道对电子态密度的最大贡献率. Bader电荷转移计算结果表明:S原子具有更强的电负性,Sn原子与S原子之间电荷转移的施主为Sn原子,受主为S原子,并且可以看出,随着层数的增加,Sn原子向S原子转移的电荷量会减小.本研究表明二维SnS的结构及电子性质对层数具有依赖性,因此可以通过改变其层数来调控其电子性质.本文的研究将对极少层SnS的合成以及少层SnS在太阳能电池和热电领域的应用提供理论指导.1 计算方法
2 结果与讨论
2.1 晶体结构预测

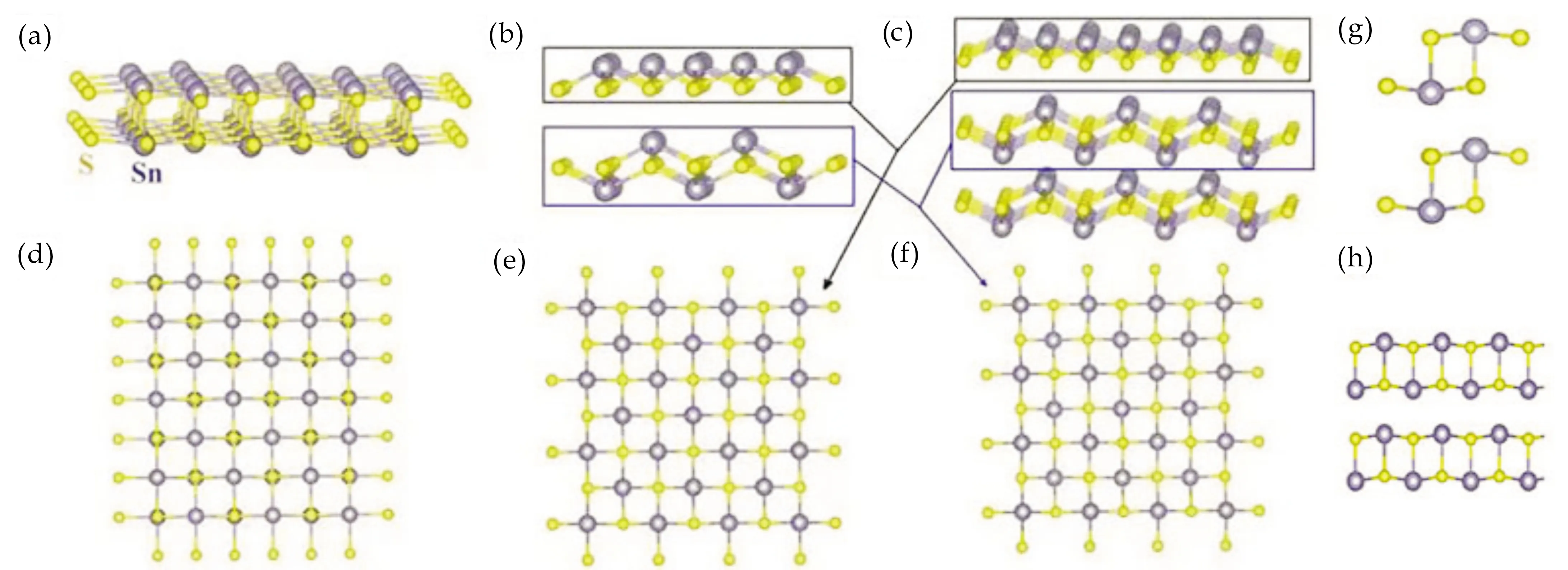
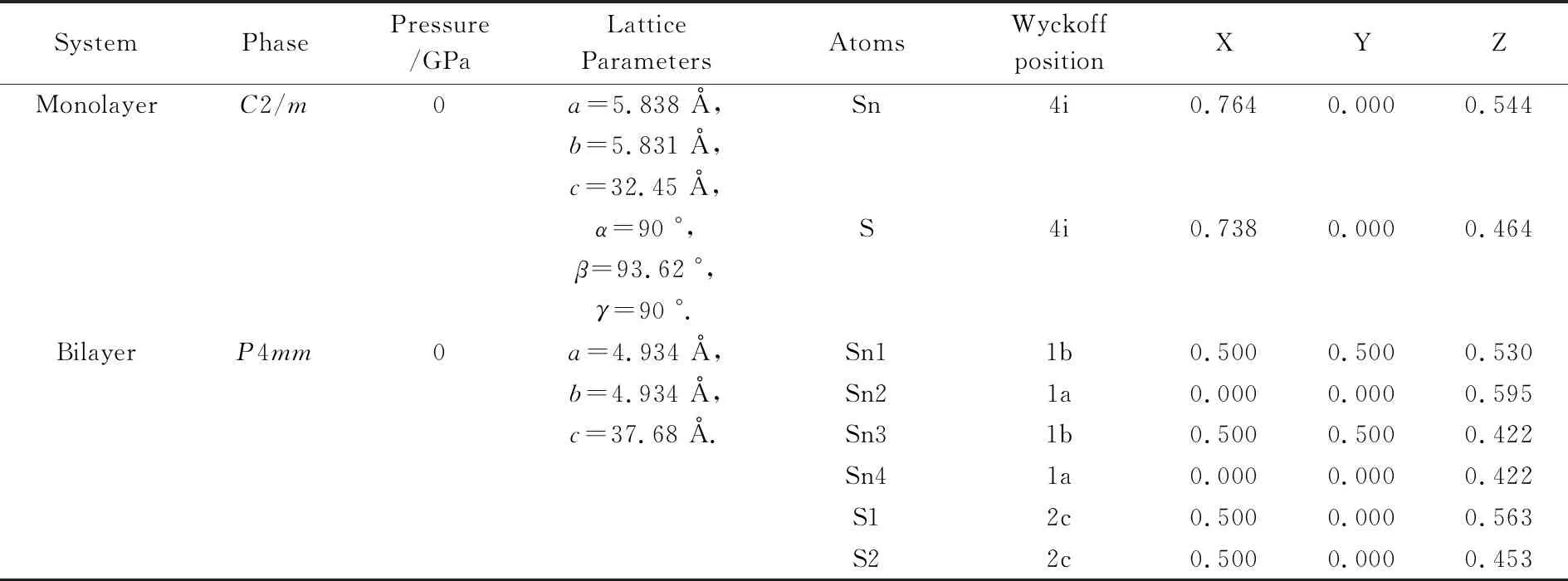
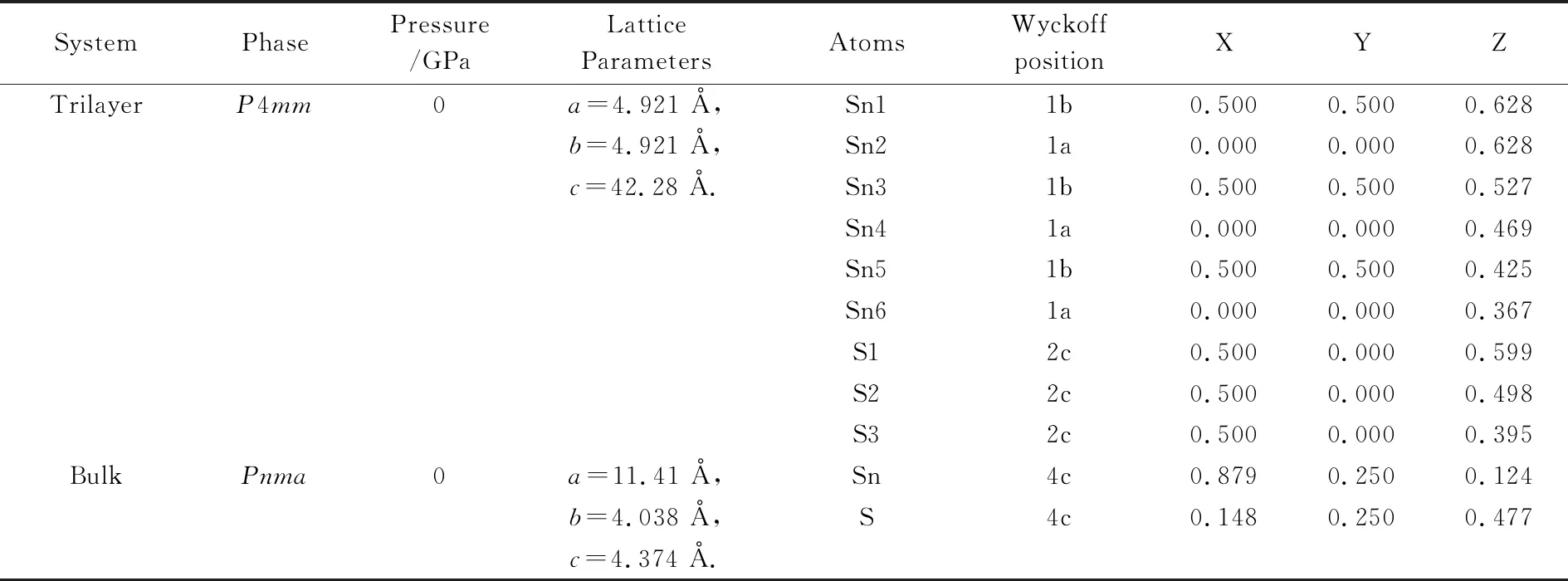
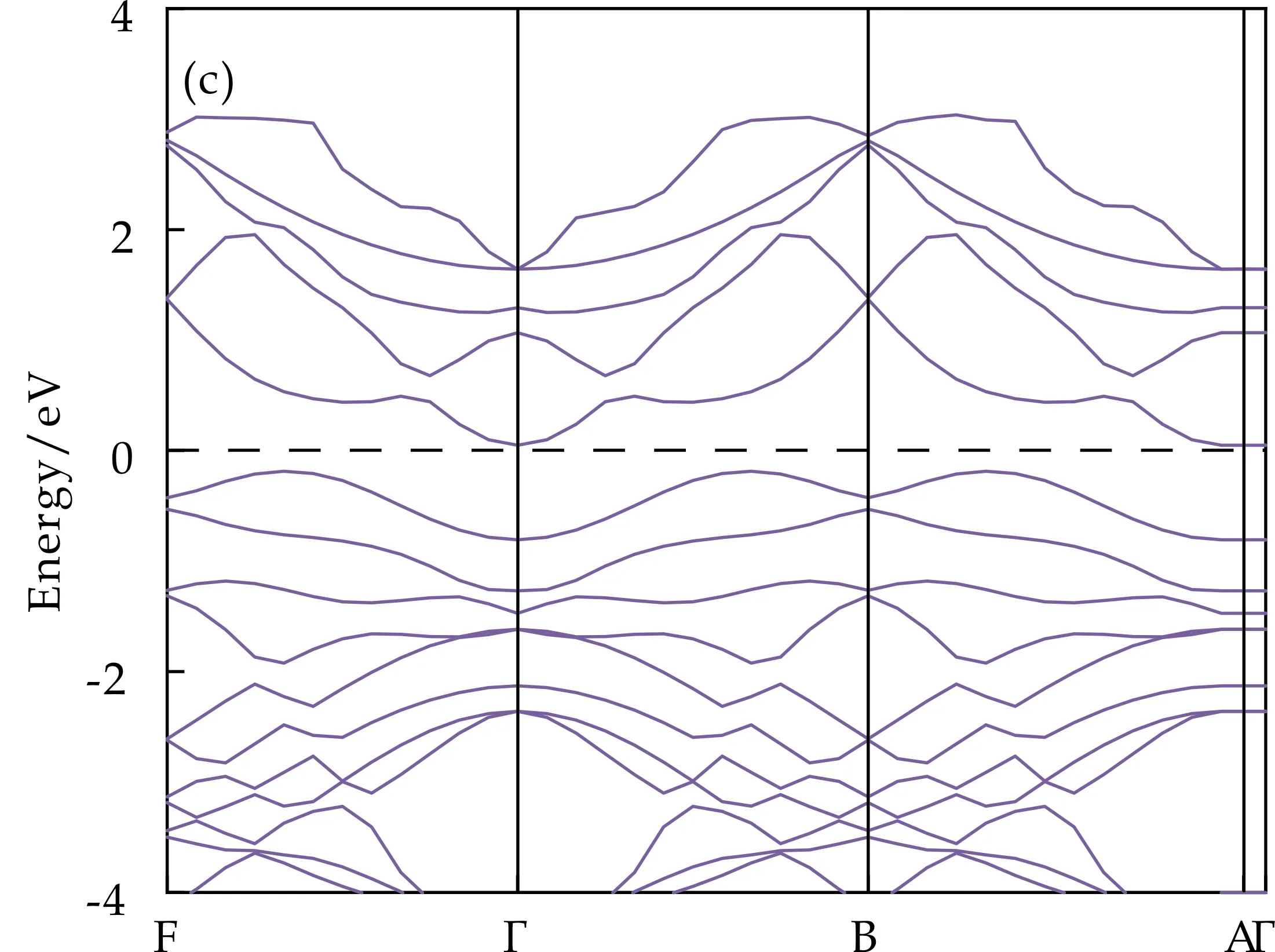
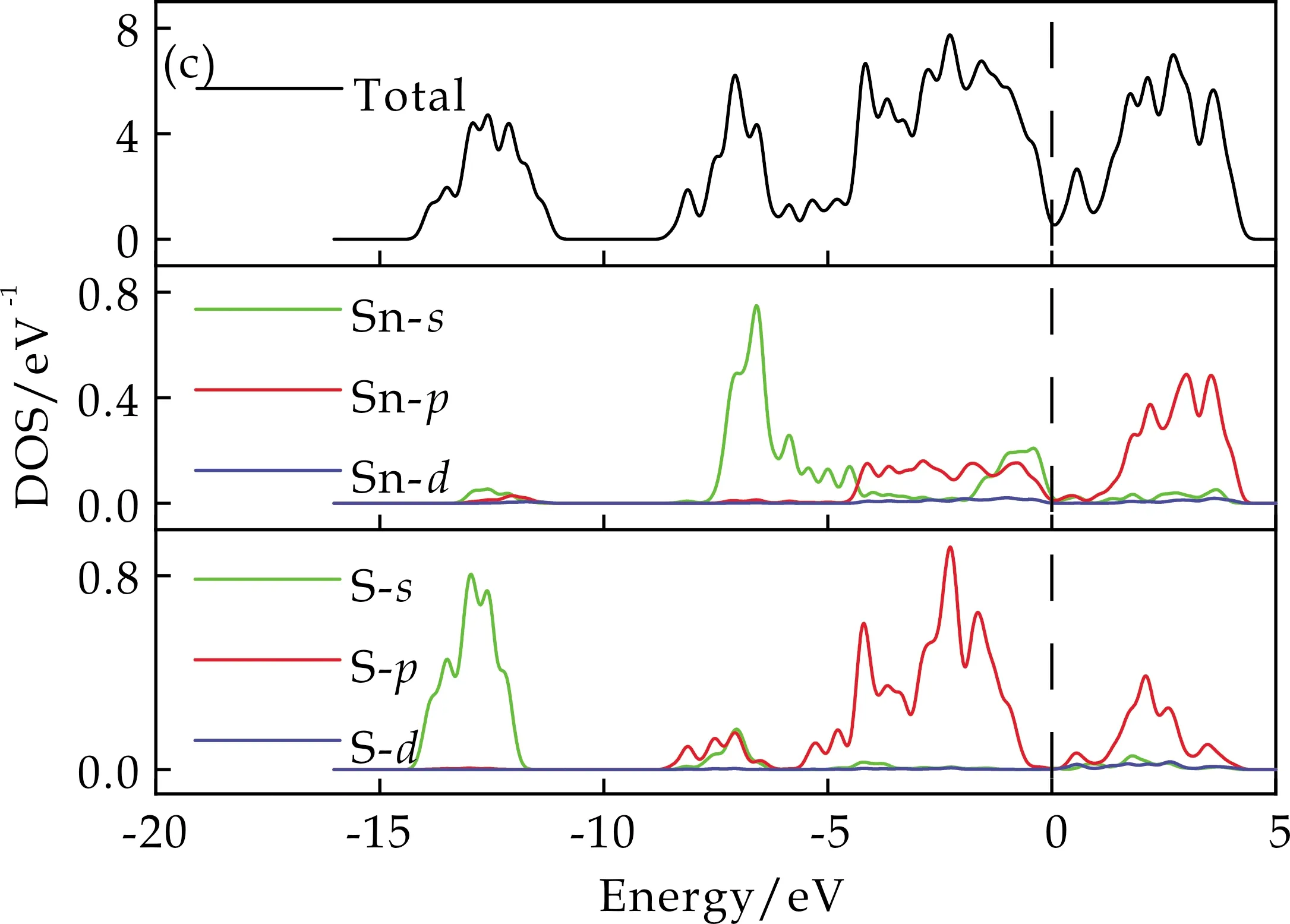
2.2 SnS的电子性质预测

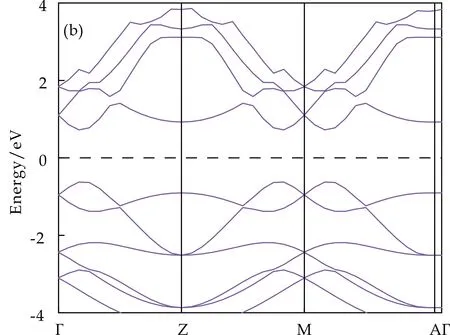









3 结论

