面向图像分类的任务驱动型分析字典学习
高 荣, 陈婵娟*, 魏 宪
(1.陕西科技大学 机电工程学院, 陕西 西安 710021; 2.中国科学院海西研究院 泉州装备制造研究所, 福建 泉州 362000)
0 引言
稀疏表示在机器学习、图像和信号处理等领域得到了广泛的应用,如图像去噪[1]、识别[2,3]、压缩[4]、分类[5,6]以及音频处理[7].具体来说,稀疏表示是利用过完备字典线性表示输入信号,其性能主要取决于过完备字典的重构性和判别性,因此字典的构建对于稀疏表示至关重要.通过使用预定义的分析字典(例如,小波字典,Gabor字典)来表示信号,可以通过简单的内积运算来产生表示系数.这种快速而明确的编码使字典学习在图像表示中非常有吸引力.此外,相对于深度学习,基于字典学习的分类算法需要较少的训练集,同时可以对非高斯噪声有较好的鲁棒性.
字典学习中一种常用的分支是合成字典学习(synthesis dictionary learning,SDL),近年来被广泛地应用于图像分类任务中.分类问题的目标是为测试样本分配正确的类别标签,所以对于这类任务来说主要关注的是字典的判别性.因此,提出了很多受监督的字典学习方法用于提高字典的判别能力.
判别性字典学习的一种常见方法是学习所有类的共享字典,强制将编码系数区分,同时训练编码系数上的分类器用于分类.Mairal等[8]提出了在编码向量空间中学习字典和相应的线性分类器.Jiang等[2]引入了二进制类标签稀疏矩阵,使得来自同一类别的样本具有相似的稀疏编码.Mairal等[9]提出了一种任务驱动型字典学习(Task-driven dictionary learning,TTDL)框架,该框架最大程度地减小了针对不同任务编码系数的不同代价函数.判别性字典学习的另一种常见的研究方法是学习结构化字典以促进不同类之间的区别,结构化的字典中原子具有类标签并且可以计算特定类的残差以促进分类.Ramirez等[10]引入一个不连贯促进项使得不同类的子字典独立.Yang等[11]提出了一种Fisher判别字典学习(Fisher discrimination dictionary learning,FDDL)方法,该方法将Fisher准则应用于表示残差和编码系数.Z.Wang等[5]从大边距的角度出发提出了最大边距字典学习(Max-Margin dictionary learning,MMDL)算法.然而,SDL的低效率限制了其发展.在现有的大多SDL方法中,由于稀疏系数可能产生更好的分类结果,因此使用l0范数或者l1范数来规范化稀疏表示.尽管近年来已经提出了很多提高稀疏编码效率的算法[12,13],但是使用l0范数或l1范数正则化仍然使得计算复杂度变高,训练和测试效率变低.
然而,作为SDL对偶变化的分析字典学习(analysis dictionary learning,ADL)越来越受到关注.S.Shekhar等[6]学习了分析字典,然后训练了SVM分类器以进行数字和面部识别.他们的结果表明,在噪声和遮挡下,ADL比SDL更加稳定,并且具有竞争优势.文献[14]和[15]都仅提出了分析字典学习的解决方案.J.Guo等[16]将局部拓扑结构和可区分的稀疏标签集成到ADL中,并使用k近邻分类器进行分类.但是关于任务驱动的ADL进行的尝试很少.
这些先前在分析词典学习中的工作都使得训练阶段的优化更简单和测试阶段的速度更快.但是,对于分类任务尚未充分利用分析字典学习.受到合成字典学习中重要方法[9,17]的启发,本文构建了受监督的任务驱动型分析字典学习(Task-driven analyis dictionary learning,TADL)模型,通过结构化的分析字典提高模型的判别性以及迹商准则(获取特征之间的关系),极大的提高了模型的分类精度.
1 字典学习
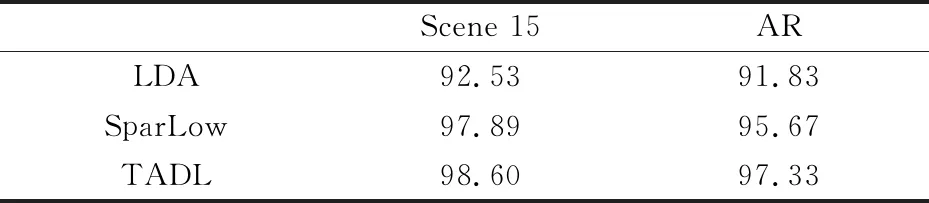
用X=[x1,x2,…,xn]∈Rd×n表n个原始样本,A=[a1,a2,…,an]∈Rm×n表示通过字典得到的X的系数矩阵.在SDL中,合成字典D=[d1,d2,…,dn]∈Rd×m(通常d (1) 式(1)中:Γ是字典D的约束集合;T是约束稀疏水平的正整数. 作为合成字典的对偶变换,分析字典学习直接将作用于特征样本,与特征变换类似,并且可以提高测试效率.分析字典Ω∈Rm×d(通常m>d)通过求解式(2)可以得到: (2) 在本节中,将充分阐述所提出的任务驱动型分析字典学习(TADL),这种方法将结构化的分析字典项[18]和迹商准则相结合,用于提高传统ADL的判别性能. 设X=[x1,…,xk,…,xK]为来自K类的一个训练数据集,其中Xk∈Rd×nk表示来自第k类的nk个样本.通过求解式(3)得到结构化的分析字典Ω=[w1,…,wk,…,wK]T: (3) 在式(3)中,第一部分:每个子字典只能将同一类中的样本转化为编码系数;第二部分:子字典Ωk将来自不同类i(i≠k)的数据转换到几乎为0的空间.这就是说,在i≠k时,Ωkxi≈0.这样的约束使得Φk具有块对角结构. 经典的降维方法是为给定的样本xi∈Rm通过相关映射(μ:Rm→Rl)寻找低维表示yi∈Rl,其中l T(l,m)={u∈Rm×l|UTU=Il|} (4) 具体来说,本文将正交投影设定为μ(x)=UTx.该模型涉及许多经典的监督和非监督学习方法,如LDA,MFA,PCA等.由于本文所要构建的任务驱动型分析字典模型属于监督学习过程,为保证整体模型的可行性,本文选择的是有监督的LDA模型. (5) ΦLbΦT (6) 式(6)中: Lb=CbΠc(Cb)T; 寻求U∈T(l,m)最优的一种常见方法是最大化迹商,即 (7) 式(7)中:矩阵A,B∈Rm×m通常为对称的半正定矩阵,本文由式(5),(6)得到.选择常数σ>0来防止分母为0. 很明显,式(7)中问题的解是旋转不变的,使得U*∈T(l,m)成为该问题的一个解.那么对于任意的Θ∈Rl×l,U*Θ是正交的.换句话说,式(7)的解集是在Rm中所有l维线性子空间的集合.为了处理这种结构引入了Grassmann流形,它可以交替地被识别为所有m维且秩为l的正交投影的集合,即 F(l,m)={UUT|U∈T(l,m)|} (8) 根据式(7)、(8),迹商问题可以表示为: (9) 式(9)中:投影矩阵P=UUT. 本节将结构化的分析字典和迹商准则相结合来构造任务驱动型分析字典学习模型,该模型是一个有效的两层表示联合学习框架,第一层为分析字典学习,第二层为迹商准则.这样利用迹商准则学习简单的稀疏表示,使得框架具有很好的分类性能.具体的代价函数如下: f:E(r,m)×F(l,r)→R (10) 式(10)中:投影矩阵P的作用是在图像的稀疏表示中捕获低维判别特征;Φ由式(3)得到;A、B由式(5)、(6)可以得到. 为了防止分析字典的解具有高度相干性,确保稀疏解的局部平滑,本文在所有分析字典中行的标量积上引入对数障碍函数来限制所学分析字典的相干性.对于分析字典Ω=[w1,…,wk,…,wK],对数障碍函数为: (11) 综上,任务驱动型分析字典学习模型的代价函数为: J:E(r,m)×F(l,r)→R J(Ω,P)=f(Ω,P)-μh(Ω) (12) 式(12)中:权重因子μ>0控制正则化项对最终解的影响. 为了求解式(12)的最优解,本文依次对TADL模型的第一、二层进行了优化求解. TADL的第一层是求解式(3)得到系数编码矩阵的最优解Φ*.首先用给定数据样本初始化分析字典Ω,然后交替更新系数编码矩阵Φ和分析字典Ω,则式(3)的优化可以在下面两个步骤之间交替进行: (1)固定Φ,更新Ω,则式(3)的优化就变为: (13) 通过将上式的一阶导数置零,可以很容易求得分析字典Ω的闭式解为: (14) (2)固定Ω,更新Φ,则式(3)的优化就变为: (15) 则Φ的闭形解为 (16) 本节,首先分析TADL代价函数的可微性,然后在Riemannian流形上利用一种几何共轭梯度(CG)算法来最大化TADL的代价函数. 3.2.1 TADL的可微性 本小节将分析TADL代价函数J的可微性并在积流形上E(r,m)×F(l,r)∈Rr×m×Rl×r计算其Euclidean梯度,这是为计算3.2.2节中J的Riemannian梯度做准备,会将Ω和P限制在该流形中. (1)计算J关于正交投影P的Euclidean梯度: (17) (2)计算J关于分析字典Ω的Euclidean梯度: (18) 式(18)中正则化项的Euclidean梯度可以很容易得到: (19) 式(19)中:ei∈Rr是Rr的第i个基向量.式(18)第一项f(Ω)的计算要求稀疏表示Φ(Ω,X)可微. (20) 为了计算f关于Ω的Euclidean导数,则需要计算Ω∈Rr×m在方向Ξ∈Rr×mΞ∈Rr×m上的方向导数: (21) 式(21)中:DA(Φ):Rr×m→Rr×r和DB(Φ):Rr×m→Rr×r是A(·)和B(·)的方向导数.由f(Ω)方向导数D1f(Ω)Ξ可以很容易得到f关于Ω的Euclidean导数. 3.2.2 一种关于TADL的几何共轭梯度算法 本节将在积流形Z=E(r,m)×F(l,r)利用几何共轭梯度(CG)算法来实现式(12)中函数J的最大化. CG算法有许多优越的特性,比如超线性收敛速度以及适用于低计算复杂度的大规模优化问题.经典的几何CG算法要求测地线和平行变换,这使得在计算上要求更高.本文引入了回缩和其相应的变换向量来替代测地线和平行变换的概念.关于本文的CG-TADL算法的流程见图1所示.具体实现过程如算法1所示. 图1 CG-TADL框架更新示意图 算法1: CG-TADL算法框架 输入:X∈Rm×n,函数A见式(6),函数B见式(5) 输出:Ω*∈E(r,m),P*∈F(l,r) (1)给定初始化 Ω(0)∈E(r,m),P(0)∈F(l,r),j=-1; (2)G(0)=gradJ(Ω(0),P(0)),H(0)=-G(0); (3)令j=j+1; (4)通过式(16)更新稀疏矩阵Φ(j); (5)令M(j)=(Ω(j),P(j)); ②计算G(j+1)=gradJ(M(j)); ③更新 H(j+1)←-G(j+1)+βVM(j),t*H(j)(H(j)),其中β的选择使得VM(j),tH(j)(G(j))和H(j+1)与J在M点的Hessian矩阵共轭; (6)如果‖M(j+1)-M(j)‖足够小,则停止迭代,否则转至步骤(3). 随后,本文将阐述CG-TADL算法的一些关键细节.首先,介绍关于积流形Z的一些基础概念.将积流形Z在点M(Ω,P)的切平面定义为: TMZ=TΩE(r,m)×TpF(l,r) (22) 其中TΩE(r,m)和TPF(l,r)分别代表流形E(r,m)和Grassmann流形F(l,r)的切平面.将流形Z从周围欧氏空间继承的Riemannian度量定义为: (23) 在算法1的每次循环中,计算J的Riemannian梯度之前,应该先计算通过式(17)和(18)来计算J关于P和Ω的Euclidean梯度,则计算J的Riemannian梯度只需将式(23)定义的Riemannian度量投影到对应切平面TMZ上,即: gradJ(Ω,P)=(grad1J(Ω,P),grad2J(Ω,P)) (24) 式(24)中:grad1J(Ω,P)和grad1J(Ω,P)分别是J关于Ω和P的Riemannian梯度.具体来说,J关于Ω的Riemannian梯度为: grad1J(Ω,P)=J(Ω)- Ωddiag(ΩTJ(Ω)) (25) 式(25)中:ddiag是将方阵的对角线元素放入对角矩阵中.函数J关于P的Riemannian梯度为 grad2J(Ω,P)=PJ(P)+J(P)P- 2P(J(P))P (26) 回缩ΓM:因为TMZ→Z是从切平面TMZ到流形Z的一个平滑映射,所以ΓM(0)=M和它的导数DΓM(0)是恒等映射(即TMZ→TMZ).在单元球(即构成流形E(r,m))的单元)中,对于w∈E(1,m),ε∈Tww(1,m)对应的回缩定义为: (27) 在Grassmann流形F(l,r)上,首先需要为P∈F(l,r)和Ψ∈TpF(l,m)构建映射关系: ζP,Ψ(t)=(Ir+t(ΨP-PΨ))Q (28) 式(28)中:t>0是更新时的步长;(·)Q是可逆矩阵唯一的QR分解.根据式(28)可将在F(l,r)上的回缩定义为: γP,Ψ(t)=ζP,Ψ(t)P(ζP,Ψ(t))T∈F(l,m) (29) 根据式(27)、式(29),将在积流形Z=E(r,m)×F(l,m)上的合成回缩按如下定义,其中M=(Ω,P)∈Z,H=(Ξ,Ψ)∈TMZ. ΓM,H(t)=([γwiεi(t)]i=1,…,k,γP,Ψ(t)) (30) 式(30)将用于完成在积流形Z上的线性搜索,即算法1中的步骤(5)-①,将式(27)中的回缩γw,ε在E(1,m)上的变换向量定义为: (31) 将式(29)中的回缩tH=(Ξ,Ψ)∈T(Ω,p)Z在F(l,m)上的变换向量定义为: (32) 最后,将合成回缩ΓM,H(t)在方向tH(t)=(Ξ,Ψ)∈T(Ω,P)Z上的变换向量通过映射VM,H:TMZ→TΓM,H(t)Z定义为: (33) 步骤(5)-③中的方向参数通过下式来更新: (34) 实验将在2个数据集上进行验证,这两个数据集为:Scene15数据集、AR人脸数据集. Scene15数据集总共有4 485张图片,被分为15类.每个类别中的图像数量从200到400不等,图像大小约为300×250像素.图像内容多样,不仅包含室内场景(例如卧室,厨房),还包含室外场景(例如建筑物和乡村景观等). AR人脸数据集包含光照、遮挡和表情变化对所选对象的影响.本实验从50位男性和50位女性中选择2 600张面部图作为数据样本. 4.2.1 参数设定 在本文所提出的模型中,有两个参数需要设置λ1和λ2,最优的λ1和λ2通过交叉验证得到,具体设置见表1所示. 表1 不同数据集的最优参数设置 当数据集为Scene15数据集时,将分析字典的原子数设置为750,每类的分析字典原子数为100.取其中的1 500张图片作为训练集,其余为测试集.当数据集为AR人脸数据集时,将分析字典的原子数设置为600,每类的分析字典原子数为6.取其中的2000张图片作为训练集,其余为测试集. 4.2.2 对比实验 实验1:将本文提出的方法与传统分析字典学习(analysis dictionary learning,ADL+SVM)[6]、投影字典对学习(Projective dictionary pair learning,DPL)[20]进行对比,实验中对不同的方法采用相同的参数设置,在Scene15数据集和AR人脸数据集上进行评估,具体结果见表2所示. 表2 在两个数据集上的分类准确度(%) 实验2:利用数据集Scene15和AR,将经典的LDA算法[19]以及低维稀疏表达(sparsese low dimensional representation,SparLow)[17]与本文方法进行对比.LDA算法使得不同类间的区别做大化,同一类内的区别最小化,以便更好地进行分类;SparLow方法是将合成字典学习与迹商准则联合学习的一种分类模型;本文的TADL方法是将结构化的分析字典与迹商准则联合学习来进行分类,与以上的两种试验方法可由直观和鲜明的对比.重点是对传统合成分析字典与本文结构化的分析字典的比较.具体实验结果见表3所示. 表3 在两个数据集上的分类准确度 (%) 从表2可以看出,本文提出的TADL方法取得了较好的分类精度.ADL+SVM由于缺少判别约束,所以分类精度较低.对于PDL方法,字典的学习没有针对每一类样本特征,而是采用了共享字典. 在实验2中,利用PCA(principal component analysis)对数据进行降维,降维后的数据见表4所示. 表4 PCA降维后数据特征维度 由实验2的结果(表3所示)可以看出,本文模型TADL比利用传统合成字典的SparLow方法的分类精度高出1%点多,验证了本文分析字典项的判别优势. 此外,实验还测试了TADL模型在数据集Scene15上对不同参数的敏感,主要的参数为λ1和λ2,通过设置:λ1=[1e-2,3e-3,8e-3],λ2=[1e-4,8e-4,1e-7].评估结果如图2所示. 图2 不同参数下TADL的分类精度图 从图2可以看出,当λ1=1e-2和λ2=1e-7时,TADL方法在Scene15数据集上的分类进度最高,可达98.6%. 至于运行效率,TADL的测试效率比SparLow、PDL以及ADL+SVM更高,它没有像l0 范数或l1 范数这样的稀疏性约束,因此大大降低了训练和测试阶段的计算复杂度. 本文主要研究了分析字典学习在图像分类中的应用,构建了一个有两层结构且受监督的任务驱动型分析字典学习模型.不同于其他ADL学习方法,本文联合学习了结构化的分析字典和迹商准则,将分类问题转化为低秩约束的判别分析字典问题,并在经典分类数据集进行了性能评估.与其他先进的分类方法相比,分类精度得到了明显提升(例如,在实验2Scene15数据集上,本模型的分类精度比字典部分使用合成字典的SparLow高出近0.7%).但是本文仅得到了具有一定判别能力且受监督的分析字典模型,适用于小样本进行学习和表达,如何提升本模型对大样本的表达精度是下一步的工作方向.2 任务驱动型分析字典学习
2.1 结构化的分析字典项

2.2 迹商准则的优化(TQ)
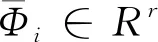
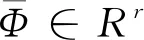
2.3 TADL模型
3 优化过程
3.1 TADL模型第一层的优化过程
3.2 TADL模型第二层的优化过程



4 实验结果与分析
4.1 实验数据集
4.2 实验设计


4.3 实验结果


5 结论

