相关滤波追踪算法中的测地线更新策略

张铭珂， 张选德

(陕西科技大学 电子信息与人工智能学院， 陕西 西安 710021)

0 引言

目标追踪是计算机视觉领域的热点问题之一，目前已广泛应用于人机交互、自动驾驶、交通控制等各个领域[1-3].单目标跟踪可以描述为：给定目标在第一帧中的位置，预测目标物体在后续帧中的运动轨迹.尽管在过去几十年中研究人员已经取得了巨大的进展，但由于存在光照变化、形变、遮挡、平面内/外旋转等问题的干扰，目标跟踪仍然是一项具有挑战性的任务[4-6].

目前，目标追踪算法主要分为判别式[7-9]和生成式两类.生成式目标追踪算法首先在初始帧中对目标物体进行建模，通过在后续帧中搜索与生成模型相似的区域来确定目标物体所在位置.生成式方法主要有卡尔曼滤波法[10]、Mean-Shift[11]以及粒子滤波[12]等.判别式目标追踪方法则是在初始帧提取正负样本，利用样本学习判别器，将在后续帧中寻找目标位置的问题转化为判断目标区域和背景区域的二分类问题.

近年来，判别相关滤波追踪算法在跟踪精度和速度之间取得了很好的平衡，备受关注.2010年，Bolme等[13]提出最小输出平方误差和(MOSSE)算法，首次将相关滤波器引入目标追踪，实现了极高的跟踪速度.2012年，Henriques等[14]通过应用循环结构和岭回归提出利用核检测追踪的循环结构算法(CSK)，在保持追踪速度的基础上，提高了追踪精度.2015年，Henriques等[15]在CSK算法的基础上，引入多通道特征的核相关滤波追踪算法(KCF)，将原本的灰度特征改为多通道HOG特征，大幅提高了追踪性能.2014年，Danelljan等[16]提出使用颜色特征的相关滤波追踪算法(CN)，使用颜色特征的追踪算法利用目标物体丰富的颜色信息，在彩色视频序列中具有较好的表现.能够有效区分目标与周围背景的特征在视觉跟踪中起到非常重要的作用.2014年，Danelljan等[8]利用尺度金字塔基于相关滤波追踪框架解决了精确估计尺度的难题.2015年，Danelljan等[7]又提出空间正则化的相关滤波追踪算法(SRDCF)，在滤波器上作用倒高斯形状的系数函数，抑制边界效应的影响，达到很好的追踪结果.2018年，Feng Li等[17]提出时空正则化的相关滤波追踪算法(STRCF)，在空间正则化的基础上引入时间正则化来控制滤波器的更新.2020年，Yiming Li等[18]在STRCF的基础上提出自动时空正则化的相关滤波追踪算法(AutoTrack).根据滤波结果响应图自动调整时间正则化项和空间正则化项，使用传统手工特征HOG在速度和精度上超越许多优秀的算法.

手工设计的特征已经不能满足追踪问题的需要，随着近年来深度学习的发展，许多跟踪器[19-23]选择使用卷积神经网络(CNNs)提取的特征作为跟踪目标的表示，在精度和鲁棒性方面取得了很大的进展.在2015～2017年，Danelljan等[23]将深度特征引入相关滤波追踪框架中，提出Deep SRDCF、C-COT[9]、ECO[5]等算法，达到较高的追踪精度.2019年，Qi等[20]使用多层CNNs特征分别计算多个追踪器，引入孪生网络来比较追踪器的结果，得到了较好的追踪结果.

视频序列中，目标物体随着时间的推移发生不可预测的变化，这种变化发生在遮挡、形变、背景杂乱和旋转等各种场景中，可能导致滤波器无法根据当前帧中的外观特征在感兴趣区域中识别跟踪目标，所以无论是使用深度网络特征还是手工特征，滤波器的更新策略至关重要.相关滤波类追踪算法近年来迅速发展，但更新策略还是沿用之前简单的加权方法，这限制了追踪算法的性能.

本文针对上述相关滤波追踪算法中滤波器的更新问题，提出一种基于正定矩阵流形测地线的改进更新策略.滤波器的更新本质上可以看作是自相关核矩阵的更新，利用前一帧与当前帧产生的两自相关核，在正定矩阵流形测地线上求得更新后的核函数矩阵，进而计算出更新后的滤波器.通过在更新中引入自相关核矩阵间的几何先验信息，在这种几何约束的基础上，更好的融合历史帧与当前帧中含有的目标物体信息，提高追踪性能.将提出的滤波器更新策略分别应用于使用HOG特征的KCF、DCF以及使用CNNs特征的TCCF，提出相应的改进更新策略的相关滤波追踪算法Ours_g、Ours_l和TCCF_l.在OTB-50公开数据集上对改进算法与相对应的基线算法进行了广泛的对比实验.实验结果表明本文所提出的更新策略可以提高追踪效果，并且能够作为一个独立模块合并于相关滤波追踪算法中，具有广泛的可推广性.

1 相关滤波追踪算法

相关滤波追踪算法[15]以学习判别器为核心，学习到的判别相关滤波器作用于连续帧中的感兴趣区域，找到滤波器响应最大的位置，即目标所在位置.训练样本xi是由目标样本循环移位产生，通过将目标样本在搜索窗口中的所有可能的平移建模为循环移位并将它们连接起来形成数据矩阵来实现，循环的结构有利于非常有效地解决频率域中以下的岭回归问题，即样本xi与其回归目标yi之间的平方误差和最小.

(1)

式(1)中：f(z)=wTz，λ为正则化参数，y为回归标签.

式(1)的最小化问题有封闭的解，可以表示为

w=(XTX+λI)-1XTY

(2)

式(2)中：数据阵X中每行代表一个样本xi，y的每个元素都代表一个回归标签，I是单位矩阵.

将上式转化到频率域求解可得

(3)

式(3)中： ∧代表傅里叶变换，▯代表元素间的乘.

KCF提出使用核技巧将线性问题的输入映射到非线性特征空间φ(x).首先将解w表示为样本xi的线性组合

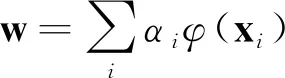
(4)

由于

φT(x)φ(x′)=k(x,x′)

(5)

可以推出

(6)

此时，α在核空间中的解为

α=(kxx+λI)-1y

(7)

由于式(7)中的kxx为循环矩阵，可得式(7)在频率域中的解为

(8)

为适应目标物体在视频序列中发生的各种变化，相关滤波追踪算法采用的更新策略为

(9)

目标响应可由下式求出

(10)

2 相关滤波追踪算法中的测地线更新策略

2.1 正定矩阵流形的测地线

流形M是一个拓扑空间，任一点的局部邻域都近似于一个欧氏空间.当M在切空间具有一个连续的度量，例如内积，则该流形可称为黎曼流形.测地线[24,25]即黎曼流形上两点间的最短曲线，测地线的长度被定义为测地距离.设M是一个黎曼流形，x,y是流形M上的两个点，γ是连接x和y的测地线，那么γ具有如下参数化形式[25]：

γx,y:[0,1]→M

s.t.γxy(0)=x,γxy(1)=y

(11)

记正定矩阵流形为Pd，对于任意的X,Y∈Pd，它们之间的测地线有闭式解[24]：

γxy(s):=X1/2(X-1/2YX-1/2)sX1/2

0≤s≤1

(12)

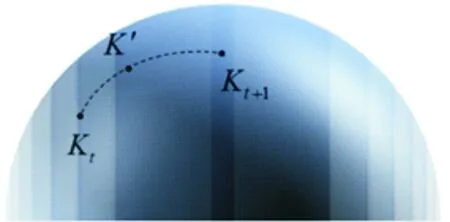
图1 基于正定矩阵流形测地线的更新策略

2.2 测地线更新策略

基于以上分析，对k′的计算如下：

(13)

由于自相关核矩阵可由离散傅里叶变换(DFT)对角化[15]，即

(14)

(15)

式(13)可以写为

(16)

由此，得到式(13)在频域的表达式.

(17)

式(17)中： 为频率域中，更新后的自相关核.

(18)

基于上述理论推导，本文在表1中给出相应的改进更新策略的相关滤波追踪算法.

表1 改进更新策略的相关滤波追踪算法

图2为基于正定矩阵流形测地线更新策略的追踪算法流程示意图.频率域中第t+1帧的特征与第t+2帧的特征进行核相关得到互相关核矩阵，通过滤波器与互相关核矩阵在时域的卷积操作，即式(10)中在频率域的相乘操作，得到响应图.根据响应图中峰值的位置预测目标物体在t+2帧中的位置.

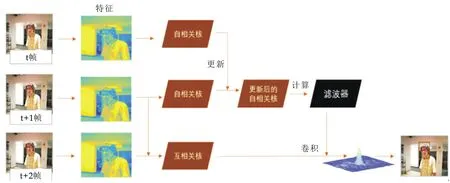
图2 基于正定矩阵流形测地线更新策略的追踪算法

3 实验结果与分析

本文提出的算法实现平台为Windows10系统Matlab2016a，计算机配置为Intel(R) Core(TM) i7-8750HCPU @2.20GHz 2.21GHz CPU，NVIDIA GeForce GTX 1070和16.0GB内存.使用VGG-16[26]网络在Caffe[27]框架上进行深度特征的提取.S的取值为0.04.

将提出的更新策略应用到使用HOG特征的核相关滤波追踪算法KCF、DCF和使用CNNs特征的TCCF[21]上.由于KCF和DCF算法分别使用的是高斯核和线性核，所以将改进算法分别命名为Ours_g，Ours_l.TCCF的改进算法命名为TCCF_l.在OTB-50[28]上对提出的算法与基线算法进行比较实验，分为定量与定性两个部分.并将提出的三种算法与其他先进的追踪算法Struck、TLD进行比较.使用的评价标准为成功率和精确率，其中成功率定义为预测跟踪框与标注跟踪框之间的重叠率超过某一阈值的帧数占总帧数的比例，精确率图定义为预测跟踪框与标注跟踪框之间的中心位置误差小于某一阈值的帧数占总帧数的比例.

3.1 定量分析

精确率图和成功率图如图3(a)、(b)所示.无论是精确率还是成功率，Ours_g、Ours_l相比其他追踪算法Struck、TLD具有更好的结果.Ours_g相对于KCF追踪算法精确率提高了0.3%，成功率持平，Ours_l相对于DCF追踪算法精确率提高了0.2%，成功率提高了0.3% .

以TCCF为基线算法的TCCF_l在两个评价标准上均有提高.在精确率上提高2.6%，在成功率上提高4%.

结果表明，无论是基于深度特征还是手工特征，在仅对更新策略进行改进的条件下都相对提升了追踪效果.虽然改进算法在总体追踪结果上提升并不大，但更新策略作为独立模块可以和目前跟踪效果领先的多种相关滤波算法结合.即本文的更新策略比原有更新策略有稍好的性能且具有广泛的推广能力.

(a)精确率图

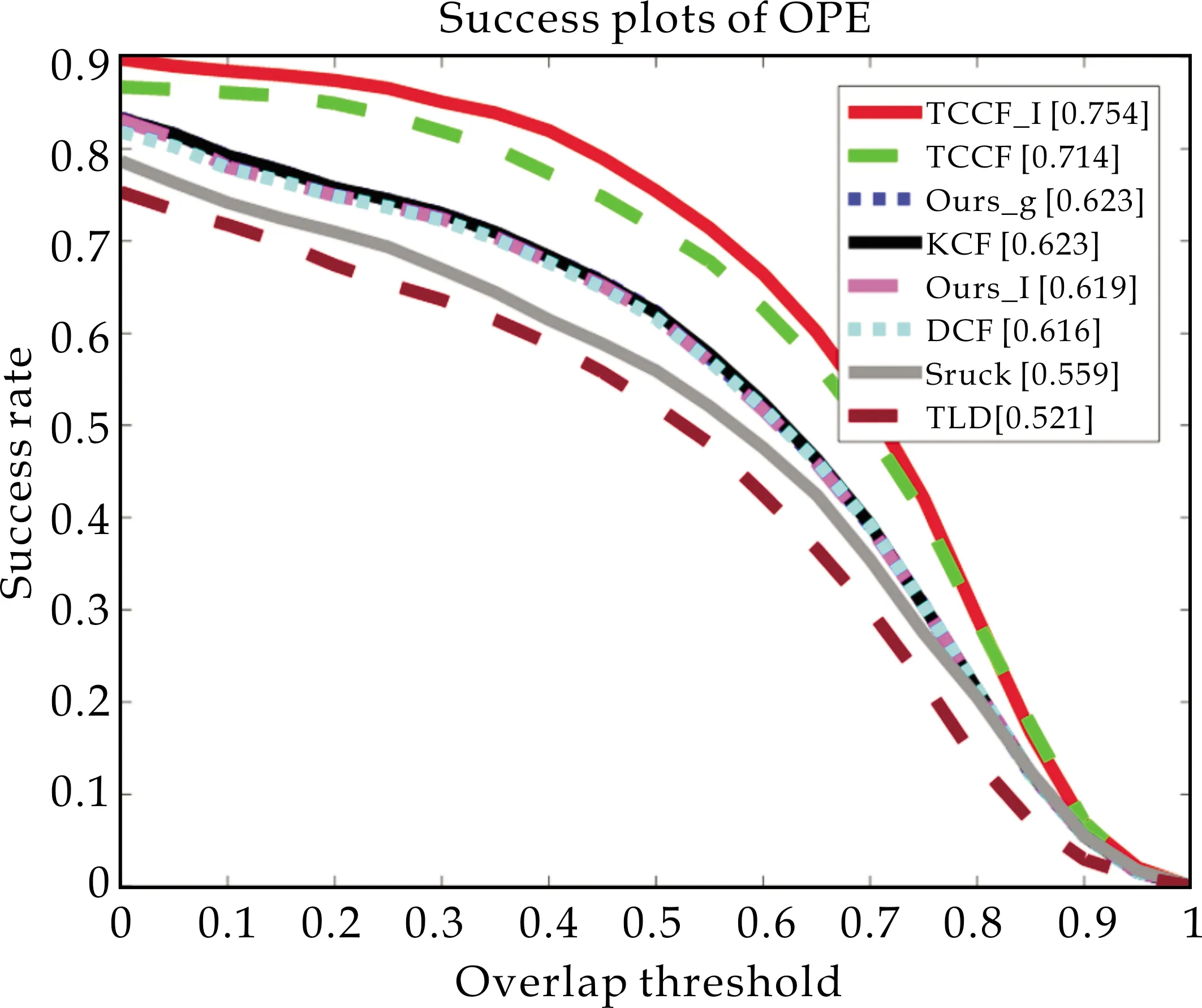
(b)成功率图图3 本文提出的算法在数据集OTB-50 上的精确率对比和成功率对比

OTB-50数据集包含多个具有不同属性的视频序列，不同属性对应于跟踪过程中可能出现的多种具有挑战性的情况，针对不同的视频属性对四个追踪算法进行评价.其中包含的属性包括：遮挡(OCC)、尺度变化(SV)、非刚性形变(DEF)、平面内旋转(IPR)、平面外旋转(OPR)、光照变化(IV)、运动模糊(MB)、快速运动(FM)、背景杂乱(BC)、超出视野(OV)以及低分辨率(LR)共11种.为了进一步比较各算法的性能，下面将对追踪器进行不同属性上的实验.

如表2所示，Ours_g在11种视频属性中的6种属性上取得了更好的精确率结果，Ours_l在10种属性上的精确率结果都超过了基线算法DCF.在表3中，Ours_g在5种属性上取得了最好的成功率结果，Ours_l在全部11种视频属性上的成功率结果都超过了DCF.上述实验结果表明，本文所提出的自相关核矩阵更新策略对比原始滤波器更新策略，相对提高了整体跟踪性能.

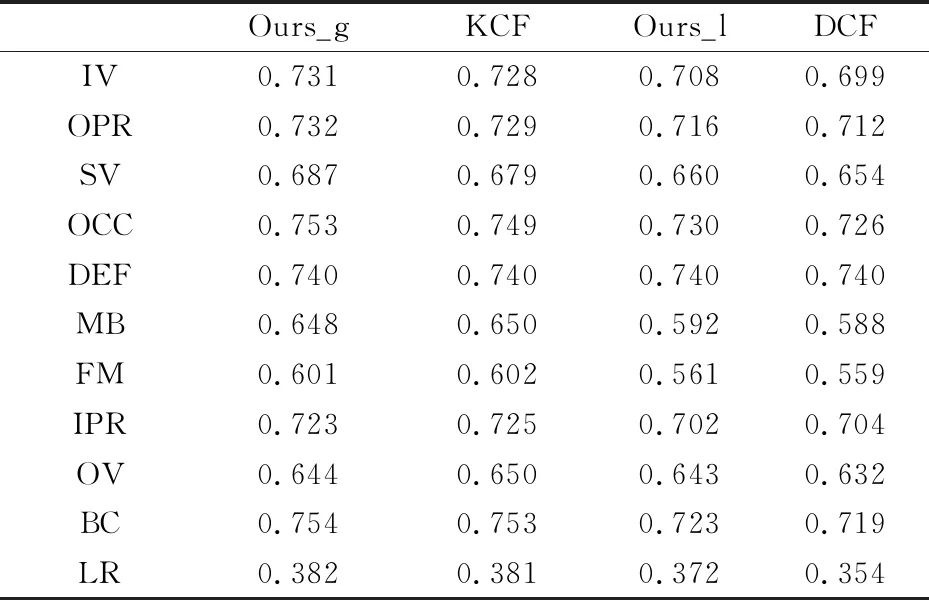
表2 4种追踪算法在11种视频属性

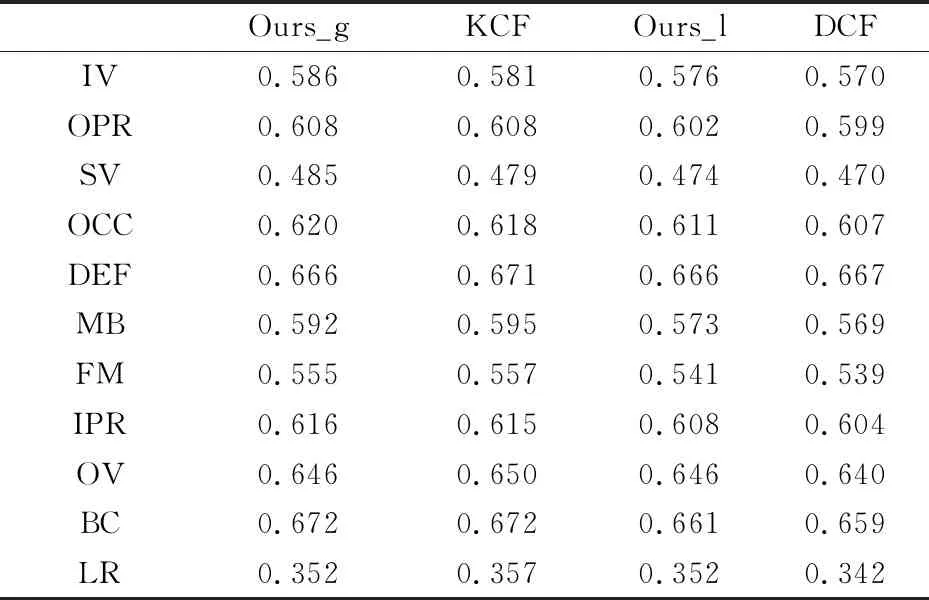
表3 4种追踪算法在11种视频属性

表4和表5是TCCF_l与其基线算法在10种不同的属性上进行的精确率和成功率比较.可以看到，在追踪精确率方面，除属性BC得到一样的结果外，其余属性改进算法的精确率均有所提高.而在成功率比较中，只有属性IV上改进算法结果稍差.

本文所提出的自相关核更新策略引入了前后两帧计算的自相关核之间的几何关系，通过利用这种几何约束，增强了追踪算法的鲁棒性.对比实验表明，追踪算法在面对视频序列中具有挑战性的情况时，本文所提出的更新策略的可行性及有效性.

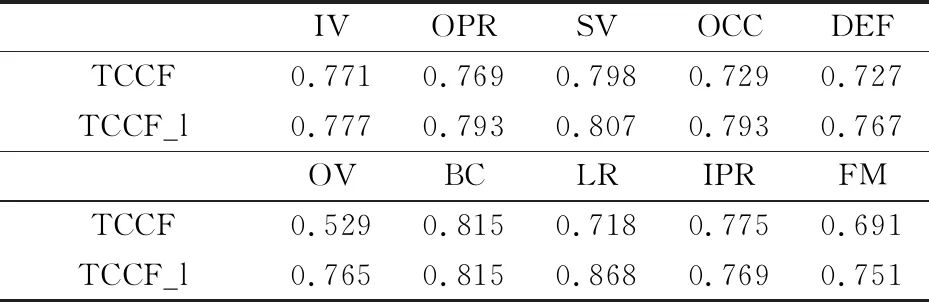
表4 2种追踪算法在10种视频属性

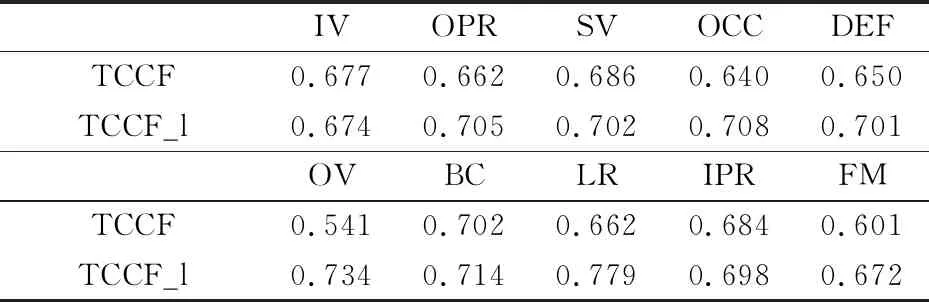
表5 2种追踪算法在10种视频属性

3.2 定性分析

这里选取了Ours_g、Ours_l、KCF、DCF 4种追踪算法在OTB-50数据集中的5个具有代表性的视频序列上的结果进行分析，分别是：Soccer、Doll、Faceocc、Suv、Bolt.这5个视频序列涉及到遮挡、形变、平面内/平面外旋转、运动模糊以及快速运动等属性.如图4所示，Soccer视频序列中，发生运动模糊以及遮挡情况时，DCF追踪算法跟踪框漂移，无法继续定位目标物体，但采用本文所提出的自相关核矩阵更新的Ours_l还能定位目标物体.这表明更新策略对追踪结果有较大的影响.

Doll视频序列以及Faceocc视频序列的追踪结果表明，目标物体在发生各种无法预测的变化时，虽然经典算法能够定位目标物体，但都存在偏移.本文所提出的Ours_g与Ours_l追踪算法，能更精准的定位目标.Suv视频序列与Bolt视频序列中，因为追踪结果相同，追踪框重叠.追踪结果表明，在基准算法KCF与DCF能准确定位目标，良好追踪时，本文所提出的算法取得了和基线算法相同的结果.

图4 4种追踪算法在5个视频序列上的追踪结果

图5展示了TCCF和TCCF_l两追踪算法在Soccer、Sylvester、Ironman和Subway四个视频序列上的追踪结果.在Soccer和Sylvester视频序列中，虽然两追踪器都能定位目标，但从Sylvester的第676帧、781帧以及Soccer的第52帧、123帧可以看出，TCCF_l可以更准确的定位目标.而在Ironman视频序列中，目标物体发生了快速运动和运动模糊等情况，此时由于使用本文所提出的更新策略，引入自相关核间的几何关系，追踪器能正确定位目标，表现出更好的追踪结果.在Subway视频序列中，因为目标行人发生了被遮挡的情况，此时TCCF_l依然能够准确定位目标，TCCF追踪器出现了跟踪框漂移.

综上，在8个视频序列上的定性分析表明，本文提出的算法在保持了原始算法优秀的追踪结果的同时，改善了原始算法表现相对较弱的视频序列上的结果.对比结果突出了更新策略的重要性，证明了引入自相关核矩阵几何约束的有效性.

图5 2种追踪算法在4个视频序列上的追踪结果

4 结论

本文针对相关滤波追踪算法，提出一种基于正定矩阵流形测地线的改进滤波器更新策略.原始算法中采用的更新策略为简单加权，这种更新策略虽然融合了当前帧与历史帧的目标信息，能达到一定的适应目标物体变化、提高鲁棒性的目的，但忽视了前后两帧自相关核函数之间本就存在的几何关系.本文提出的自相关核函数更新策略正是基于这种关系，将前后两帧图像产生的自相关核矩阵在一定的几何约束下融合，求得更加鲁棒的滤波器，以达到更好的追踪效果.在OTB-50上对使用不同特征的相关滤波追踪算法进行了实验，结果表明，本文所提出的更新策略在不影响追踪速度的基础上，提高了算法的追踪性能.另外，该更新策略是一种适用范围广、可迁移的更新策略，可以作为独立的模块与相关滤波类追踪算法进行融合，具有广泛的应用前景.