DC/DC变换器虚拟直流电机控制稳定机理研究

尹英龙， 刘宝泉

(陕西科技大学 电气与控制工程学院, 陕西 西安 710021)

0 引言

直流微电网是一种新的组网形式[1-3]，配电方式为直流，并、离网均可运行.与交流微电网相比，直流微电网无需考虑频率、无功功率、谐波等因素[4,5]，接纳可再生能源的可靠性高[6]，有利于发电、储能装置和直流负荷的接入[7].由于主要接口为电力电子变换器，系统惯性低、阻尼小，负荷、电源的频繁投切和功率波动会引起直流母线电压的波动，影响到整个系统的稳定运行.

直流并网变换器的控制特性对于维持直流电压的稳定，提高直流微网的效率和抗干扰能力具有重要作用，针对直流微电网中DC/DC变换器的控制策略是目前的关键所在[8].研究人员针对单个以及多个并网变换器提出了主从控制、电压-电流下垂控制、分层控制等方法，但这些方法并未有效地改善系统的惯性与阻尼特性[9-11].

类比交流微电网中增加虚拟惯性和虚拟阻尼抑制交流系统的电压和频率波动[12-17]，研究人员在直流微电网进行了大量研究.文献[18]将下垂控制和改变等效输出阻抗相结合，但该方法不利于深入分析虚拟控制对微电网系统稳定性的影响机理.文献[19]提出一种虚拟惯性控制策略及总线信号传输方法，但该文献主要研究协调控制，并未给出虚拟惯性控制的详细分析.文献[20]提出应用超级电容器，提高了系统的虚拟惯性，但增加了成本.文献[21]和[22]在直流级联系统中加入虚拟电阻，改善DC/DC变换器的动态特性.文献[23]提出一种阻性虚拟阻抗进行补偿的下垂控制策略，但本质上未改变高通滤波器的属性.目前关于虚拟直流电机的研究主要是将电机方程代入后进行稳定性分析和参数设计，并未深入分析虚拟惯性和虚拟阻尼是怎样的工作机理，尤其是如何影响带宽、幅相频裕度、超调量等控制系统中参数的变化.

本文建立了虚拟直流电机的小信号模型，推导出虚拟直流电机的传递函数，以控制系统通用的传递函数，在时域和频域中分析了虚拟直流电机对控制系统的影响机理.进一步以BUCK变换器为研究对象，具体分析虚拟惯性和虚拟阻尼两个参数对控制系统中参数的影响，最后通过仿真验证了分析结果的合理性.

1 虚拟直流电机环节的基本原理

1.1 虚拟直流电机环节的构造

理想的直流电机的电气特性和机械特性是构造虚拟直流电机环节的基础，构造虚拟直流电机控制环节需要用到如下方程：

(1)

式(1)是在扭转弹性转矩但不忽略阻尼转矩的理想情况下直流发电机运动控制系统的基本运动方程和机械方程，其中J为机械转动惯量，ωm为转子的机械角速度，Te为电磁转矩，Tm为机械转矩，D为阻转矩阻尼系数，再使输入量为转矩差，输出量为角速度ω.由于最终要将输出量电枢电流Ia作为DC/DC变换器的输入量，所以需要将角速度ω作进一步转化，先得到电枢电动势E，再得到电枢电流Ia，并将电流作为反馈回路的输入量，先得到电磁功率Pe，最后得到电磁转矩Te作为反馈回路的输出量，由此可以绘制图1所示的虚拟直流发电机环节的结构框图.

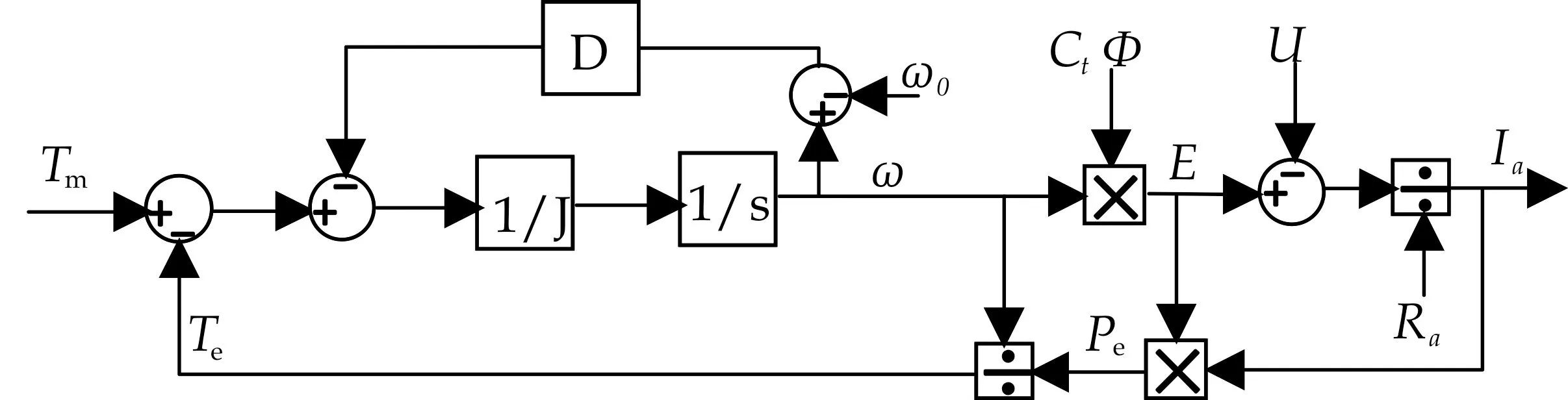
图1 虚拟直流发电机环节的结构框图

通过加入虚拟直流电机环节，可以建立双闭环控制系统中电压环与电流环的联系.

1.2 虚拟直流电机环节传递函数的推导

图1所示虚拟直流发电机环节的控制框图结构比较复杂，也考虑到后面需要对整个控制系统进行小信号建模和分析，对这一环节进行逐步简化，最终推导出虚拟直流电机环节的传递函数.

本着由内环到外环的化简原则，先对图1所示的部分结构进行简化，通过节点的移动，可以将含有机械转动惯量J和阻转矩阻尼系数D的环路解开，带有复杂乘除运算的部分结构可以计算后化简，最后通过式(2)得到传递函数，可以看出虚拟直流电机控制环节为一阶惯性环节.

(2)

2 虚拟直流电机环节致稳的通用性结论

2.1 对控制系统时域的影响分析

时域分析有四个动态性能指标，分别是上升时间tr，峰值时间tp，调节时间ts，超调量σ%.用tr或tp评价系统的响应速度；用σ%评价系统的阻尼程度；而ts是同时反映响应速度和阻尼程度的综合性指标.在控制系统中，除了那些不容许产生振荡响应的系统外，通常都希望控制系统具有适度的阻尼、较快的响应速度和较短的调节时间.

既然虚拟直流电机控制环节可以等效为一阶惯性环节，为简化对控制过程的分析，原系统通过负荷侧电压调节，用PI双闭环控制单个对象，同时假设该控制对象有m个极点，n个零点(待分析的系统结构如图2所示)，进一步对虚拟直流电机对零极点分布、稳定裕度、幅值裕度带来的影响进行分析.

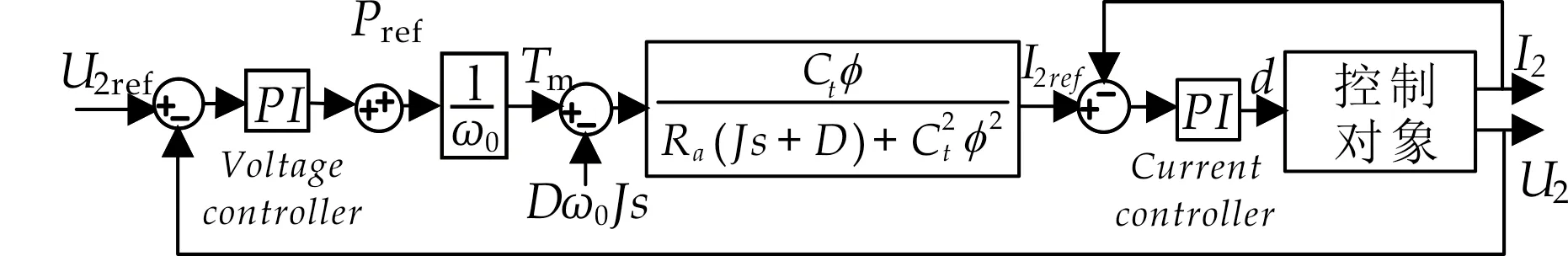
图2 含有虚拟直流电机环节的控制系统框图

原(m-n)阶系统的开环传递函数为：

(3)

由于时间常数反映系统的惯性，原系统的惯性越小，响应速度越快；反之，惯性越大，响应越慢.

加入虚拟直流电机控制后，系统增加了一个开环极点：

(4)

虚拟直流电机控制环节使原系统增加一个开环极点，会使根轨迹曲线向右偏移，且所增加的极点越靠近虚轴，影响越大，且这种影响对系统的动态性能改善是不利的.由于式(4)中各参数均为实常数，虚拟直流电机环节为系统增加的是一个实极点，对根轨迹的影响较小.具体来说，增加开环实极点后，根轨迹会增加至(m+1)条，根轨迹渐近线也增加到(m+1)条，且渐近线与实轴的夹角会随之变化，与实轴的交点也会随之变化且随D的增大和J的减小越来越远离虚轴.

对于高阶系统的动态性能，距离虚轴最近的闭环主导极点在系统的时间响应过程中起主导作用.在实际控制系统中，常会把高阶系统的增益调整到使系统具有一对闭环主导极点，以减少非线性因素(如死区、间隙和库仑摩擦)等对系统性能的影响，虚拟直流电机环节为系统增加的极点为闭环非主导极点，会增大系统响应的峰值时间，减缓系统的响应速度，但会减小超调量σ%.此时这个增加的实极点可以在一定程度上增加系统阻尼.由于这种作用会随闭环极点接近虚轴而加剧，D的减小和J的增大恰好可以达到这种效果.非主导极点会增大系统的阻尼，而超调量仅与系统的阻尼比有关，则J越大，D越小，系统的阻尼越大，系统的超调量越大.

由式(4)可知，D越小，s的绝对值越小，闭环极点越接近虚轴，而J在分母中，J越小，s的绝对值越大，闭环极点越远离虚轴.

增加虚拟直流电机环节的系统开环传递函数可以将该环节化为一阶惯性环节的标准形式，如式(5)所示.

(5)

对比一阶惯性环节的标准形式，可以得到J与标准形式中的时间常数τ的变化成正比，而D则与τ的变化趋势相反；标准形式中的开环增益K与D的变化趋势相反，而与J无关.控制系统的开环增益与D有关，且与其变化成反比关系，增加的开环极点的位置与J和D均有关，且J越大D越小，开环极点越远离虚轴.

由式(5)可知，设虚拟直流电机环节带来的时间常数为TG，J越大，D越小，TG越大，响应速度越慢，由于系统的带宽越大，时域的响应速度越快，所以D的减小和J的增大通过降低系统的响应速度，也在一定程度上减小了系统的带宽.

2.2 对控制系统频域的影响分析

利用控制系统开环对数幅频特性曲线对加入虚拟直流电机前后的变化展开分析.一阶惯性环节的交接频率为该环节传递函数中s系数的倒数，即：

(6)

不妨将原系统时间常数Ta的值从大到小重新排列，转折频率的大小不同，斜率变化位置亦不同，通过调整D和J的值使得ω1的值最小，开环对数幅频渐近线特性曲线在此转折频率斜率降低20 dB/dec.

应用开环对数频率特性判断闭环系统的稳定性的方法之一，是在L(ω)为正值的频段内，对数相频曲线是否穿过-180 °线，若未穿过则稳定，反之则不稳定.原系统为稳定系统，则在L(ω)>0 dB的频段内对数相频特性不会穿越-180 °线.引入虚拟直流电机控制技术后，系统转折频率减小，穿越频率会随之减小，从而可以适应更大开环增益K的需要.

系统频域内的相对稳定性常用相角裕度γ和幅值裕度h来度量，稳定系统和非稳定系统的相角裕度和幅值裕度在半对数坐标图中的表现不同：稳定系统穿越频率在截止频率之后，相角裕度和幅值裕度均为正值；非稳定系统穿越频率在截止频率之前.那么虚拟直流电机带来的惯性环节可以使原来稳定的系统的截止频率前移，通过调整D和J，使增加的时间常数大于原控制系统中任意一个时间常数，使系统状态更加稳定.

相角裕度和幅值裕度在对数坐标下的计算公式分别为：

(7)

通常情况下，利用相角裕度进行判定，即相角裕度大于零，系统是稳定的，而且该值越大，系统越稳定.但是对于幅值裕度，指的是相角为-180 °时对应的幅值.虚拟直流电机环节给系统增加一个小的转折频率，而截止频率不是转折频率，是对数幅频曲线经过0 dB时对应的频率.所以增加的转折频率会使相角裕度增大，系统较原系统更加稳定.

频率范围在0～ωb称为系统的带宽，其中ωb称为带宽频率.虚拟直流电机控制环节的加入会减小带宽频率，从而减小系统带宽.设输入信号的带宽为0～ωM，噪声信号集中起作用的频带为ω1～ωn，则控制系统的带宽频率通常取为5～10ωM.且使ω1～ωn处于0～ωb范围之外，虚拟直流电机所带来的系统带宽的减小无疑可以更加远离噪声信号的影响区间.

虚拟直流电机环节通过增加一个开环极点，降低了开环系统的转折频率从而降低了系统带宽，但是由于这一环节的加入，使系统的响应速度变缓.

3 虚拟直流电机环节对BUCK变换器稳定性的影响

3.1 虚拟直流电机控制下的BUCK变换器小信号传递函数

下面对电压电流双闭环控制的稳定BUCK电路引入虚拟直流电机环节做小信号下的传递函数推导.

对BUCK变换器状态空间方程组施加小信号扰动，设开关管开通时间所占百分比为d，经过拉氏变换和整理，可以得到输出电流对占空比d和输出电压对输出电流的传递函数：

(8)

假设原系统为稳定系统，电压环传递函数有m个极点、n个零点，加入虚拟直流电机控制技术，可将式(8)中的小信号模型代入整理，即可得到加入虚拟直流电机环节的BUCK变换器的开环传递函数为：

(9)

虚拟直流电机控制环节所带来的一阶惯性作用明显，转折频率大幅度减小，带宽会随之减小，同时增大了相位裕度，如图3的Bode图所示.

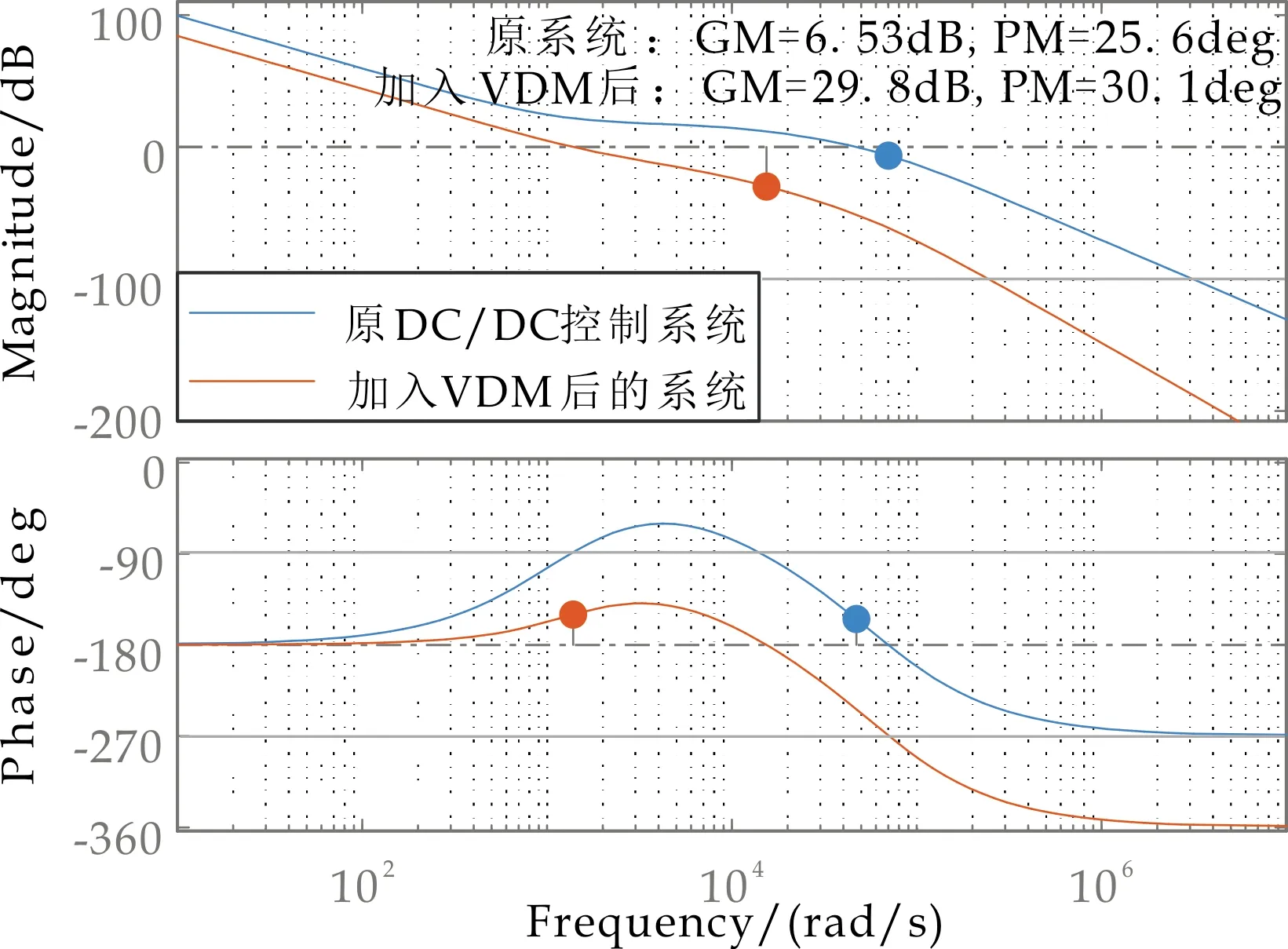
图3 加入虚拟直流电机(VDM)前后的Bode图

3.2 虚拟直流电机参数对BUCK变换器控制系统的作用

利用控制变量法分别改变惯性参量和阻尼参量的取值探究两个参数对BUCK变换器的控制系统稳定性的影响机理.

图4表示将阻尼参数D由20增加到50，再增加到100的三组Bode曲线.可以发现，随着D的增大，中低频区间对数幅频特性曲线下降速度减缓，整个系统开环增益逐渐降低，对数相频曲线随着频率的升高对应相角被抬高.验证了D对系统开环增益的影响为：D越大，系统的开环增益越小.也可以通过D对频率走势的影响，说明D对极点位置的影响为D越小，极点越远离虚轴.

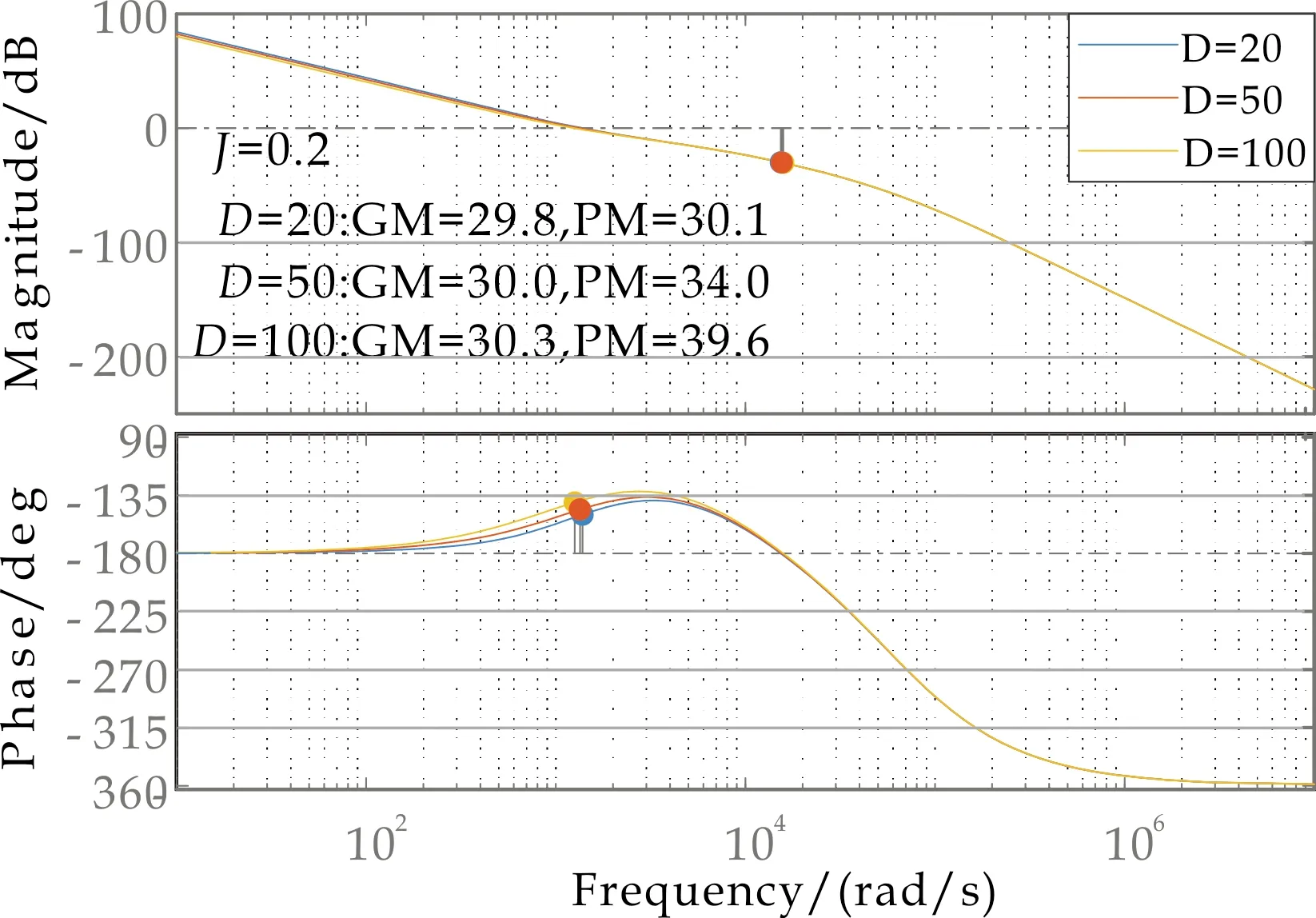
图4 改变虚拟直流电机阻尼参数D的Bode图

图5表示将惯性参数J由0.2增加到0.5，再增加到0.7的三组Bode曲线.幅值裕度GM先减小再增大；相位裕度PM逐渐减小.也可以发现随着J的增大，转折频率逐渐减小.继而可以说明J对系统开环极点位置的影响为：J越大，极点越远离虚轴.

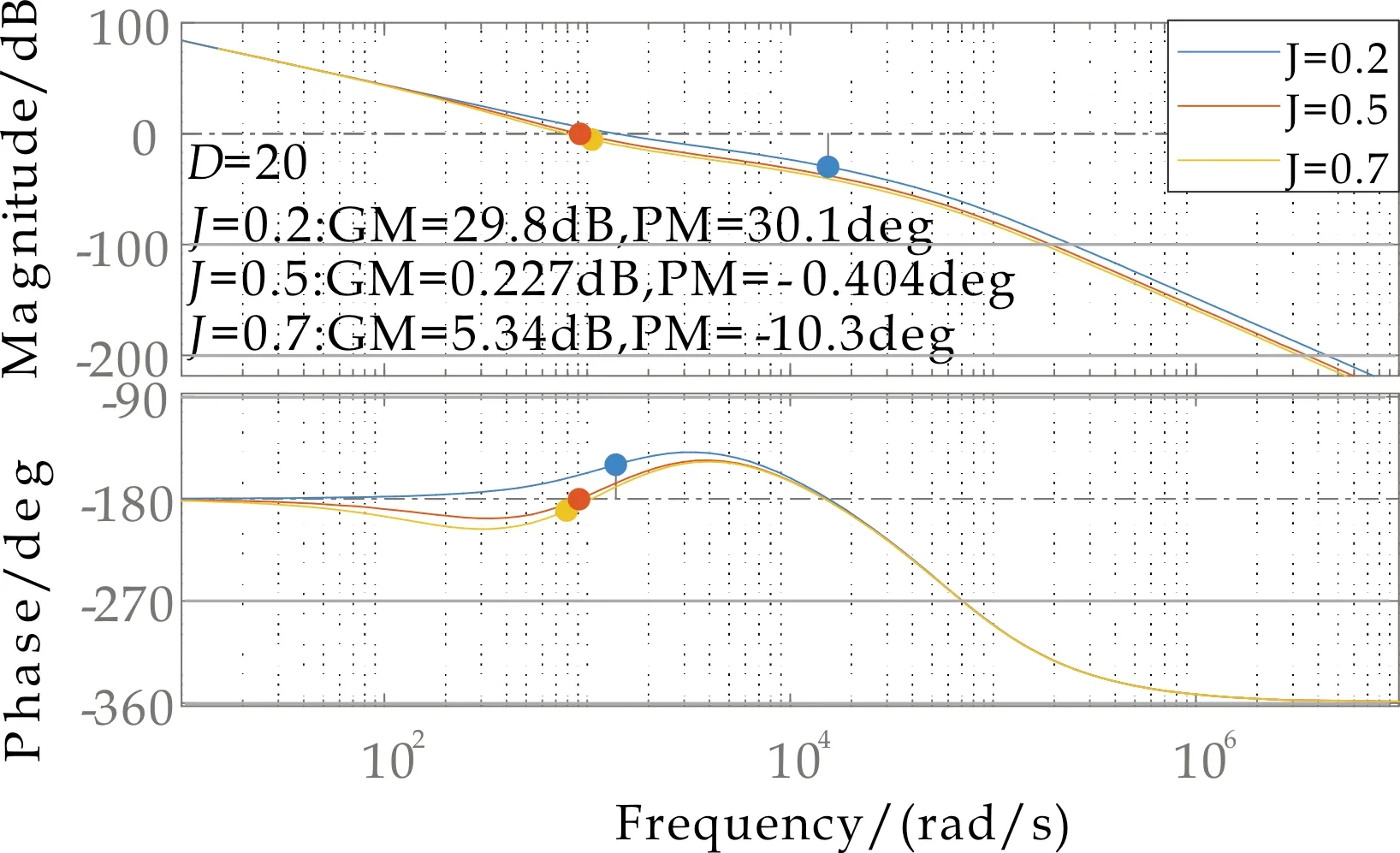
图5 改变虚拟直流电机惯性参数J 的Bode图

4 电路仿真和测试结果

4.1 加减载仿真结果

仿真所用到的电路控制框图如图6所示.控制方式采用电压电流双闭环，电流内环以电感电流为控制对象，电流控制器采用比例积分控制；电流外环以电容电压为控制对象，电压控制器采用比例积分控制，在此基础上将虚拟直流电机控制环节加入外环之中.

原控制系统是电压电流双闭环的稳定系统，稳定后输出电压100 V，空载时输出电流10 A，加入虚拟直流电机后，会给系统增加一个极点，虚拟直流电机的部分参数如表1所示.

图6 含有虚拟直流电机环节的buck 变换器控制框图

表1 虚拟直流电机部分参数

为验证加入虚拟直流电机环节的控制系统与原BUCK控制系统的稳定性，在输出电压稳定后任一时刻对电路负载侧(图7中为0.025 s)加载一次，负载阻值分别为1 Ω和10 Ω.

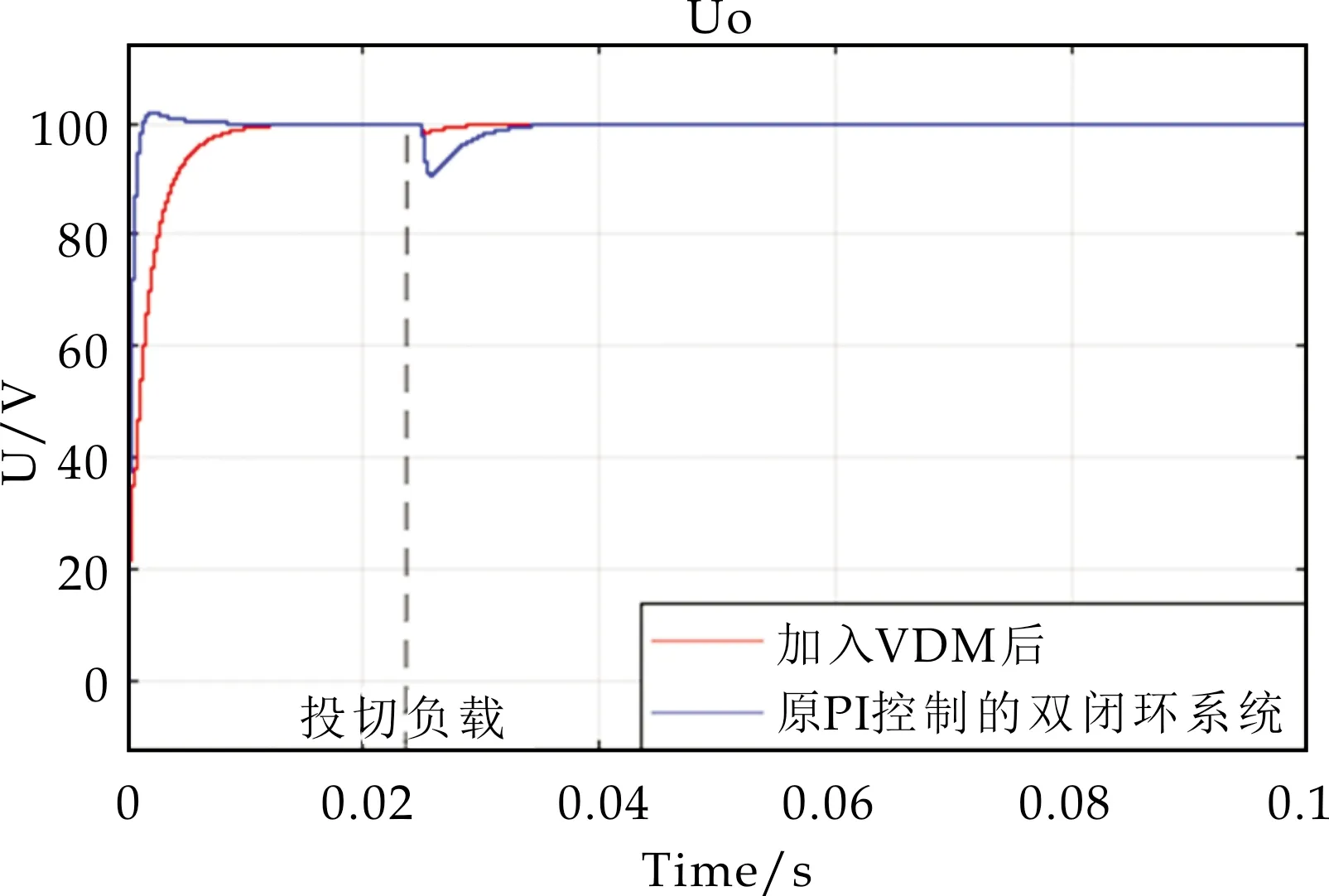
(a)负载侧投切1 Ω电阻

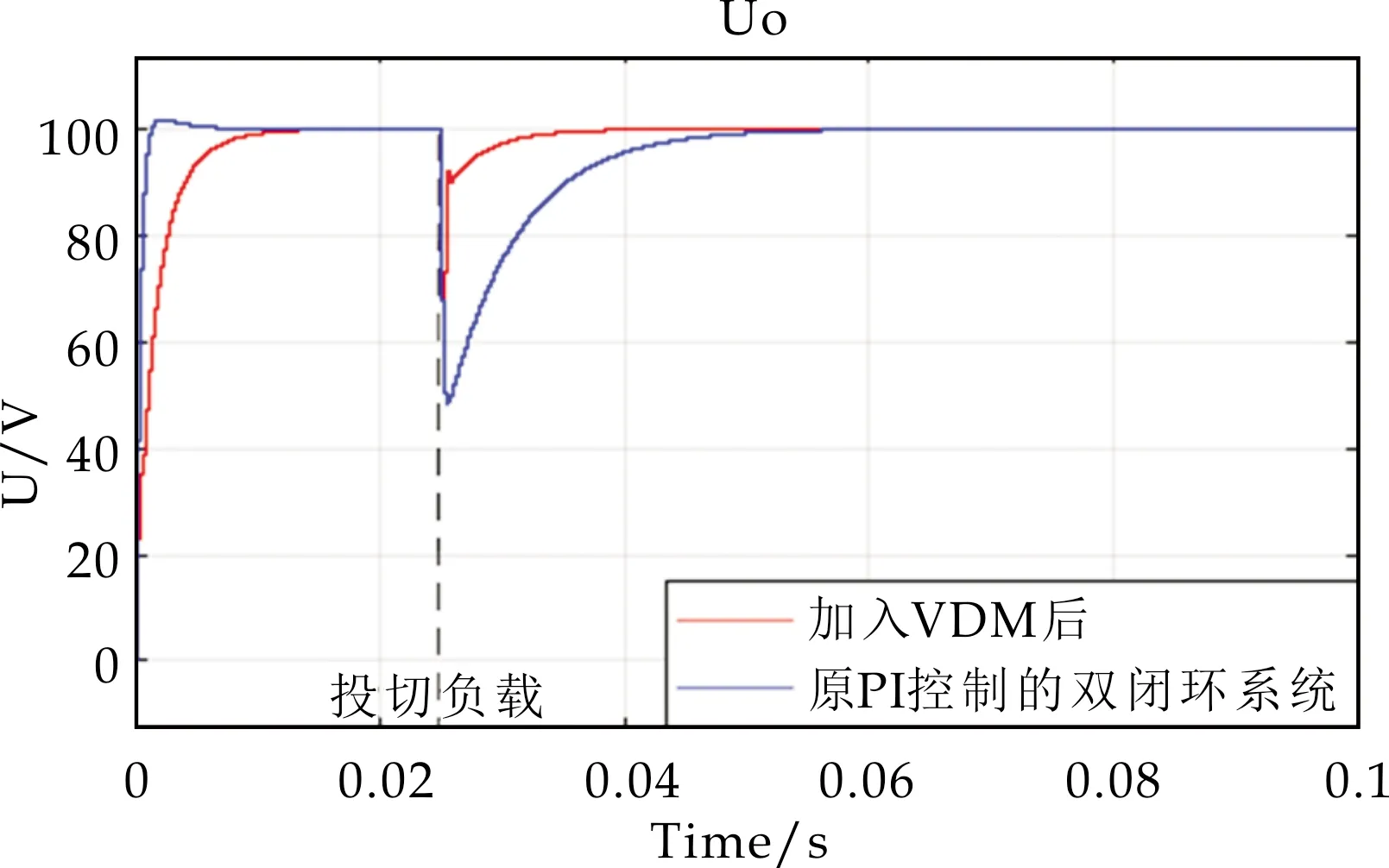
(b)负载侧投切10 Ω电阻图7 加入虚拟直流电机控制技术 前后的系统响应图

由系统加入虚拟直流电机控制技术前后的响应图可以得出，虚拟直流电机控制环节的加入使原来稳定的系统上升时间增大，从而减慢了系统的响应速度.另一方面，在小负载扰动下，原双闭环控制系统电压波动较大，而虚拟直流电机控制技术控制的系统较原系统更稳定.

4.2 改变参数仿真结果

以下对虚拟直流电机参数对控制系统的影响进行验证.利用控制变量法，分别改变惯性参数J和阻尼参数D，得到系统的响应曲线，如图8所示.在D不变的情况下，逐渐增大J的取值，系统的调节时间增大，同时上升时间增大，系统阻尼增大，超调量增大，稳态误差增大，这就验证了J与延迟时间的变化趋势相同，即J越大，延迟时间越长.在J不变的情况下，逐渐增大D的取值，系统调节时间减小，系统阻尼减小，超调量减小，稳态误差减小，说明D与延迟时间的变化趋势相反.而增益与D的变化趋势相反，与J的变化无关.

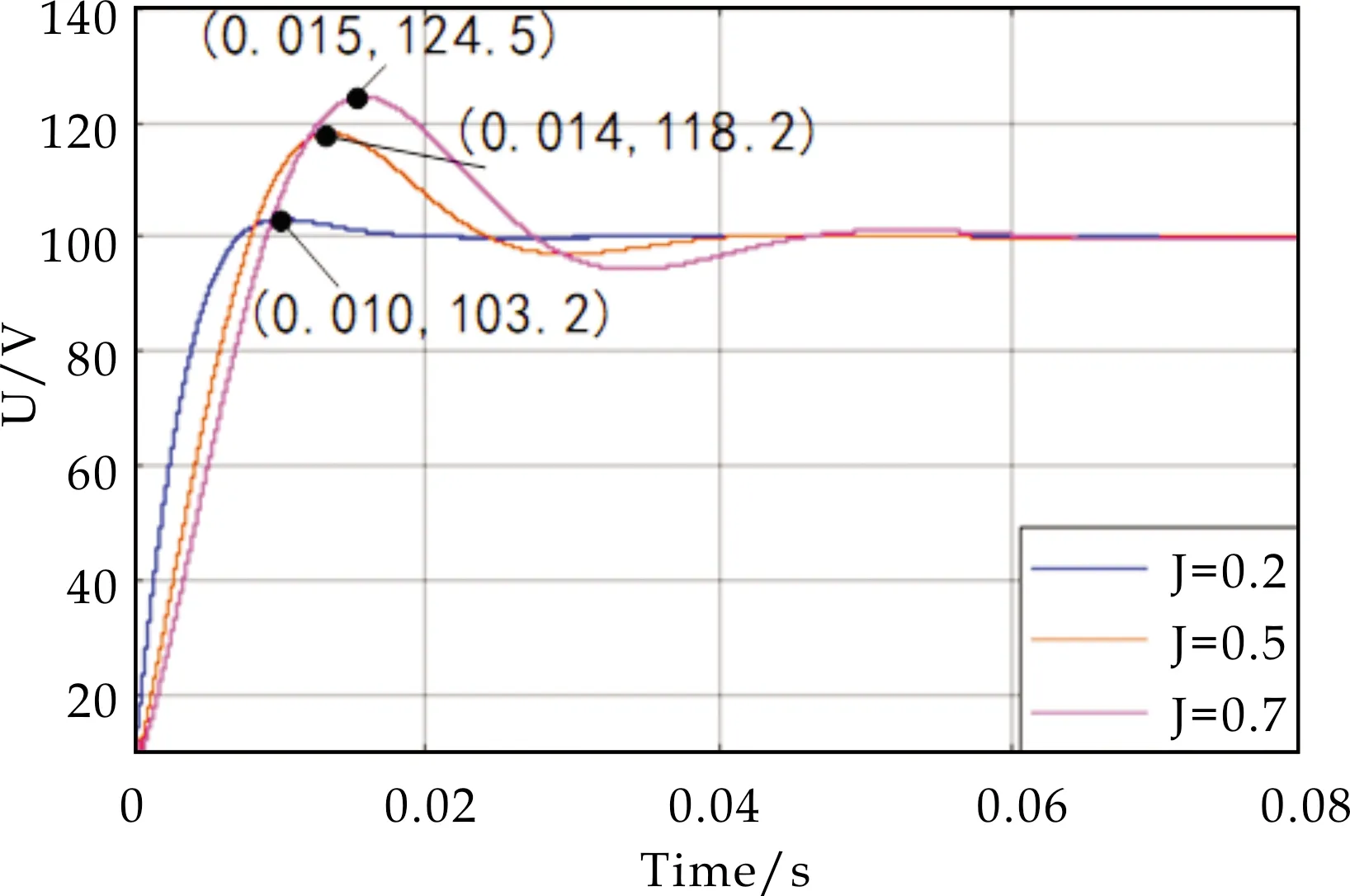
(a)J取不同值时的输出电压波形

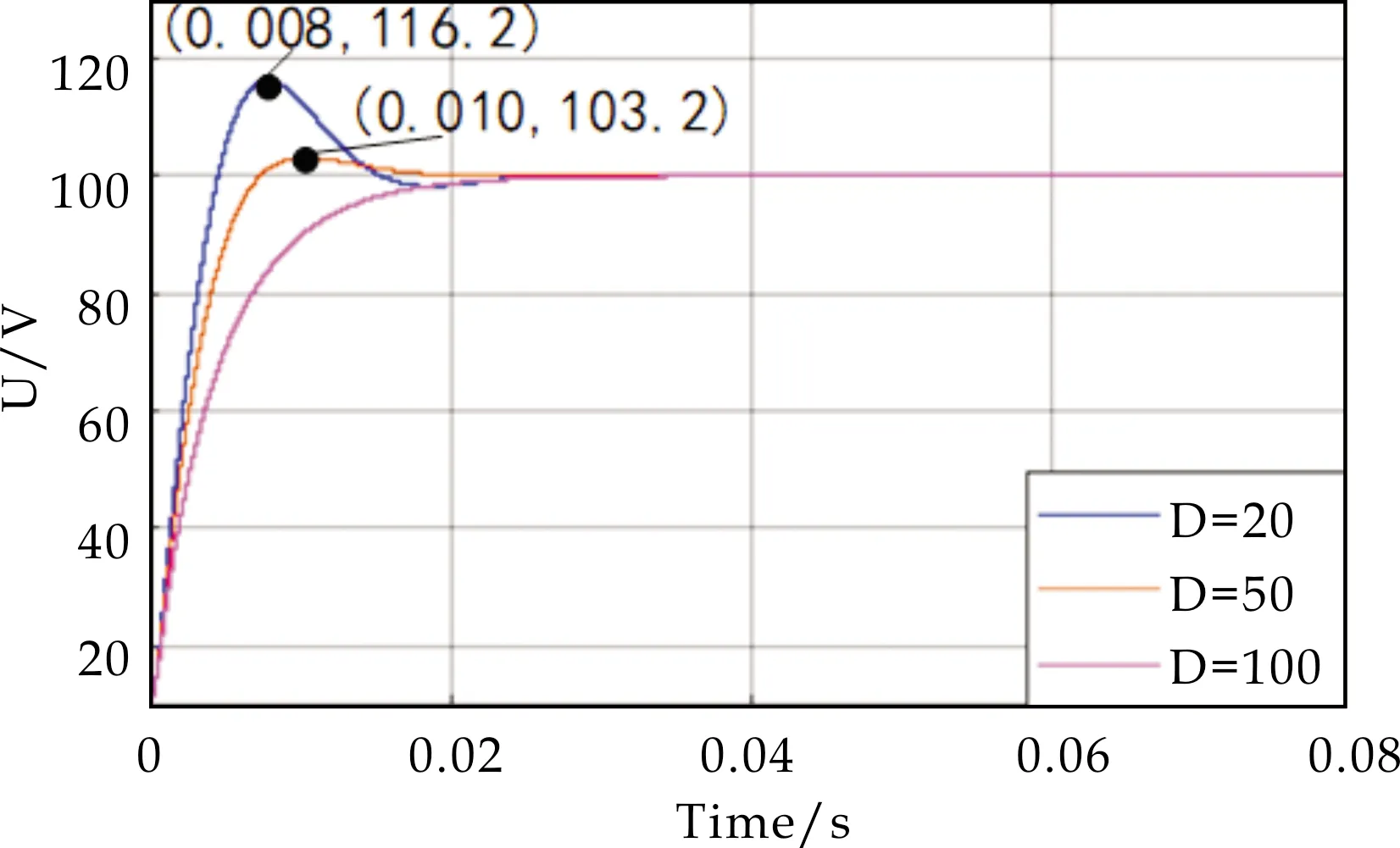
(b)D取不同值时的输出电压波形图8 改变虚拟直流电机参数的系统响应图

5 结论

虚拟直流电机控制技术对提高直流微电网稳定性具有一定效果，为使该技术能够更好地改善DC/DC变换器的稳定性，本文对虚拟直流电机控制策略进行了研究，并得出以下结论：

(1)通过构造虚拟直流电机在小信号下的结构框图，并经过一系列结构化简得到了虚拟直流电机可以等效为一阶惯性环节.

(2)通过在时域内对虚拟直流电机控制的DC/DC变换器的理论分析，发现控制系统的开环增益与D有关，且与其变化成反比关系，增加的开环极点的位置与J和D均有关，且J越大D越小，开环极点越远离虚轴.再结合频域内的系统稳定性分析方法，发现虚拟直流电机环节通过增加一个开环极点，降低了开环系统的转折频率从而降低了系统带宽，但是由于这一环节的加入，使系统的响应速度变缓.

(3)通过对虚拟直流电机控制的BUCK电路进行小信号建模，利用控制变量法分别改变惯性参量和阻尼参量的取值验证了两个参数对BUCK变换器的控制系统稳定性的影响机理，即J的增大会增加系统的延迟时间，D的增大则会缩短系统的延迟时间，系统的增益与D的变化趋势相反，而与J的变化无关.

(4)本文提出的虚拟直流电机的通用性结论可以应用于改善典型DC/DC变换器的稳定性.