Excel 在化学动力学教学中的应用

鲍 霞，汪雪梅，张晓艳

（淮南师范学院 化学与材料工程学院，安徽 淮南 232038）

化学动力学是研究化学反应速率和反应机理的化学分支学科，通过化学动力学的研究，可以知道如何控制反应条件，提高主反应的速率，增加产品产量，抑制副反应的速率，减少原料消耗，减少副产物，提高纯度，提高产品质量，所以，化学动力学的研究有理论与实践上的重大意义［1］。 化学动力学涉及到的公式多、形式复杂，无论是计算速率常数，还是确定反应级数，都涉及到复杂运算，手工计算工作量大，很多数据计算采取近似处理，结果不够准确， 学生对这些近似处理方法的理解停留在表面，对所学内容理解不够深刻。 计算机技术的进步使很多计算简化，而把数据转化为图像，给学生形象化展示数据变化规律，更有助于加深学生对知识的理解。 因此，引入计算软件到化学动力学的课堂教学中就有着重要的意义。 目前，在解决化学动力学计算方面涌现出了很多新方法。 利用DynaFit、Tenua、Materials Studio、Visual Basic 和 Matlab 等软件进行计算［2-6］，可以解决复杂的动力学计算，但需要学生具有一定的编程能力，具有较高的计算机应用水平。 Excel 是office 软件的一个重要组成部分， 它拥有丰富的数据处理函数和绘制图表功能，运算快速准确，广泛应用于管理、统计分析、金融、工程计算等众多领域。 Excel 无需编程，界面友好，计算过程简单， 能够直观地展示计算过程和方法，在教学举例中具有很好的适用性［8-9］。本文就 Excel在化学动力学计算方面的应用进行实例探讨。

1 快速求反应的活化能和指前因子

《无机化学》在讨论温度对反应速度的影响时，有个经典例题，根据一组数据（5 个不同温度时的反应速率常数），求反应的活化能Ea、指前因子A及566K 时反应速率常数k。 目前的教材和相关习题在处理这类问题时，一般用计算法，取两组数据进行计算，教材［10］例 4-2 取 576K 和 781K 的 2 组数据进行计算，得到活化能Ea=168.3kJ/mol，进而得指前因子 A=2.4×1011mol-1·dm3·s-1，再将 566K 代入求得此时反应速率常数 k=7.1×10-5mol-1·dm3·s-1。此种方法，事实上只用了2 个温度的数据，没有考虑其他数据，误差较大；如果取不同的温度进行计算，结果也不相同。传统手工作图，虽然将所有实验数据都纳入考查范围，但不宜求得斜率和截距。

利用Excel， 可以轻松求得上述数据， 方便快捷， 结果准确。 根据阿伦尼乌斯公式对数形式可知 lnk 与 1/T 有线性关系，直线的斜率为，截距为lnA。 具体操作如下：

第1 步：我们将实验数据输入A2:B6 单元格。

第 2 步：在 C 列求出 1/T ，D 列求出 lnk（见图1）。

第3 步：利用SLOPE 函 数 求 出 直 线 斜率。SLOPE 函数：返回根据 known_y's 和 known_x's 中的数据点拟合的线性回归直线的斜率。 语法：SLOPE(known_y's,known_x's)。 此例 Known_y's 为 lnk，也就是 D2:D6 单元格的数据；Known_x's 为 1/T ，也就是C2:C6 单元格的数据。

第4 步： 利用INTERCEPT 函数求出直线截距。 INTERCEPT 函数：返回函数图形与Y 轴交点到原点距离。 语法：INTERCEPT (known_y's,known_x's)，函数参数和前面函数一致。此例参数为(D2:D6,C2:C6)。

第6 步：求出任意温度的反应速率常数。 已知直线斜率和截距，根据公式（1），可得k=e^(G1/G6+G2)，G1/G6 为斜率/温度 T。

第7 步：G2 为直线截距。将需要求的温度数据填入G6 单元格，在G7 单元格中建立公式【=e^(G1/G6+G2)】，随即就可求出相应温度的反应速率常数k。

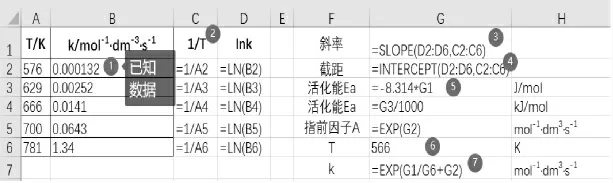
图1 求算活化能和指前因子数据输入

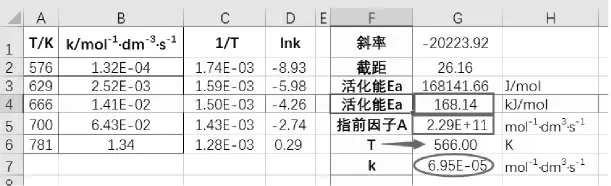
图2 求算活化能和指前因子数据输出

如果用在学生实验，可以轻松考查不同学生做出的数据，还可利用CORREL 函数，给出数据的相关系数［=CORREL(D2:D6,C2:C6)］，本例相关系数为-0.999 95，其绝对值非常接近1，相关性很好。

2 求解反应速率方程和反应级数

反应速率方程是化学动力学部分的重要内容，反应aA+bB=gG+hH 某一时刻的瞬时速率r 与反应物浓度之间符合如下关系式：r=kc(A)mc(B)n，此式称为反应的速率方程， 式中k 称为反应速率常数，该反应的反应级数为：m+n。

教材根据下表实验数据 （B3:D8）， 建立反应2NO+2H2=2H2O+N2的速率方程， 根据公式r=kc(A)mc(B)n，上述反应的速率方程可以表示为:

在教学中，我们经常是通过改变其中一种反应组分浓度，固定其他反应物浓度，通过观察或单变量作图，求出某反应组分的级数；接着再改变另一种反应组分浓度，固定其他组分，求出这种反应组分的级数。 操作复杂，计算繁琐。

将上述速率方程（2）两边取对数得lgr = m lgc

利用Excel 的数据分析工具中的多元回归，可轻松求出各个不同反应物对反应瞬时速率的影响，给出速率方程。 操作如下：

第1 步：输入原始数据。 将数据输入Excel 的B、C、D 列。

第2 步：计算对数值。 再将B3:D8 区域数据取对数放到F3:H8 区域（见图3）。

第3 步：调用分析数据库。

①点击左上角的选项按钮，然后点击“Excel 选项”，在“Excel 选项”界面中，选择左侧的“加载项”，然后点击“转到”按钮。②勾选“分析数据库”。③选择Excel 主界面上方的“数据”选项，然后点击“数据分析”。④在分析数据库中选择“回归”分析选项，然后点击“确定”按钮（见图4）。⑤设置参数。输入：Y 值输入区域：$H$3:$H$8，X 值输入区域：$F$3:$G$8；置信度：可选择默认的95%；输出选项：可选择新工作表，为了便于对照比较，选择本表的空白区域，左上角起始单元格为A10 单元格，设置输出区域：$A$10（见图5）。⑥点击确定后，结果输出。⑦关于 lgr 与 lgc(NO)、lgc(H2)的多元回归分析完成（见图6）。

图3 求解反应速率方程数据输入

图4 调用数据分析工具

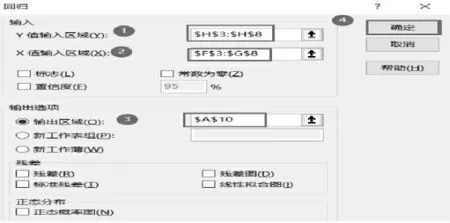
图5 回归分析参数设置

图6 回归分析结果输出

图6 中最后部分是“回归参数表”：B26：B28 为线性方程的截距和x1、x2的系数， 据此可得出估算的回归方程为：y=2.034 7x1+0.960 1x2+4.912 0

对应方程lgr=mlgc(NO)+nlgc(H2) +lgk 可知：m=2.034 7≈2，n=0.960 1≈1，lgk=4.91 20

由于 lgk=4.912 0， 所以，k=10b=8.17×104dm6·mol-2·s-1

重要的是图6 中的E26-E28， P-value 为回归系数t 统计量的P 值。通过观察发现本例中的此数值， 即t 统计量的P 值均远小于显著性水平0.05，因此，均与y 显著相关。

通过上述计算， 可得该反应的速率方程为：r=kc(NO)2c(H2)= 8.17×104*c(NO)2c(H2)

此反应对反应物NO 为2 级反应，对反应物H2为1 级反应，反应总级数为3。

3 考查温度对反应速率常数的影响

第1 步：在A1 到A3 单元格分别输入“活化能Ea”、活化能数值(本例输入 168.3)、“kJ/mol”。

第2 步：在A4 到A6 单元格分别输入“指前因子 A”、指前因子数值(本例输入 2.40E+11)、“mol-1·dm3·s-1”。

第 3 步：在 B1 单元格输入“T (K)”，B2 单元格输入起始温度（本例输入500），在B3 单元格输入公式“=B2+10”（根据不同情况，可以输入不同温度间隔，本例相邻温度相差为10K，k2=k1+10），利用填充柄，向下输入到需要的数值，本例填充到B32（800K）。

第 4 步：在 C1 单元格输入“lgk”，C2 单元格输入公式 “=-A$2*1000/(2.303*8.314*B2)+LOG10(A$5)”， 注意公式中A2 和A5 单元格引用要用绝对引用，利用填充柄，向下输入到需要的数值。

第5 步：计算反应速率常数k，在D1 单元格输入“k”，在 D2 单元格输入公式“=10^C2”，利用填充柄，向下输入到需要的数值。

第6 步： 计算相邻单元格反应速率常数比值，在 E2 单元格输入“k2/k1”，在 E2 单元格输入公式“=D3/D2”（见图7 和图8）。

图7 温度对反应速率常数的影响数据输入

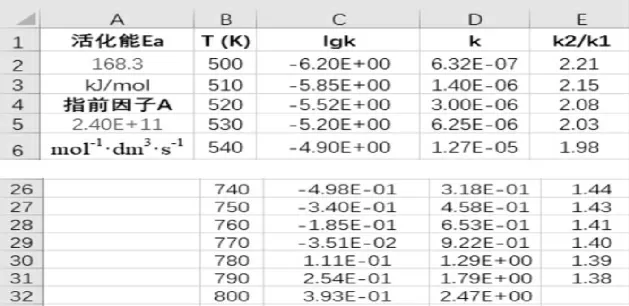
图8 温度对反应速率常数的影响数据输出

第 7 步：选中 B、D、E 列，选择“插入”功能区中的“散点图”。

第8 步：设置坐标轴格式，横坐标刻度最小值500，最大值 800。

第9 步：用鼠标右键点选系列2（k2/k1）数据线，在弹出的选项卡里选择“设置数据系列格式”，选择“系列选项”中的系列绘制在“次坐标轴”。

教材中只利用数据计算2 个温度区间的速率常数值，虽然得出结论：对于同一反应，在低温区段升高10K 时，速率常数k 增大的倍数较大；而在高温区段，速率常数k 增大的倍数较小。 学生对速率常数变化规律没有深刻认识，我们用Excel 计算可以轻松得到一系列温度对应的速率常数k 值，可清晰看出，随着温度升高，k2/k1的值是逐渐减低的，我们还可以将数据用双Y 图显示出来， 从图示可看出，虽然低温段升高10K，速率常数变化值(k2/k1)较大， 但速率常数的绝对数值却很小， 温度在700K以上，反应速率常数才迅速增加（见图9）。

图9 温度对反应速率常数的影响

4 结语

将 Excel 软件应用于化学动力学教学中，不需要编程，计算简便、快速、准确，使学生摆脱繁琐的手工计算，提高了学生解决复杂问题的能力，增强了学生的计算机应用能力， 提升了学生学习兴趣，加深了对知识的理解。