四轮转向汽车的操纵稳定性分析
范 英,訾慧鹏,谢纯禄,冯韶华
(太原科技大学交通与物流学院,太原 030024)
四轮转向控制技术(4WS)的诞生,极大地提升了汽车的操纵稳定性和安全性。很好的改善了传统汽车低速转向灵活性差,高速转向稳定性差等缺点[1]。曾宇[2]以二自由度4WS模型为基础,对4WS汽车的操纵稳定性进行仿真分析,验证了4WS汽车的优越性。刘泽明[3]在Simulink中搭建二自由度线性模型,通过阶跃仿真验证了4WS汽车高速稳定优越性。郭子蒙[4]在二自由度模型的基础上,对比了两种不同控制算法下4WS汽车的操纵稳定性。以上的研究很好的证明了四轮转向系统的优越性,但在模型的选择上未考虑车身的侧倾和轮胎的侧偏特性,易导致较大的误差。因此本文在二自由度4WS模型基础上,考虑车身侧倾和轮胎侧偏特性,建立4WS三自由度非线性模型,并对二自由度线性模型和三自由度非线性模型的操纵稳定性进行仿真对比分析。
1 4WS模型的搭建
1.1 二自由度模型
四轮转向车辆二自由度模型即自行车模型,为方便计算,近似的认为车辆只有侧向运动和横摆运动,如图1所示。
图中:δf,δr分别为汽车前、后轮转角;a,b为质心至前后轴距离;u为车身纵向速度;v为车身侧向速度;β为质心处侧偏角。
在研究四轮转向车辆二自由度模型时需要作如下的假设:
(1)汽车纵向速度恒定不变;
(2)忽略转向系统影响,直接输入前后轮转角;
(3)忽略悬架系统的影响;
(4)忽略空气动力的影响;
(5)轮胎侧偏特性呈线性。
二自由度模型的动力学方程如式(1)所示。
(1)
1.2 三自由度模型
在上述二自由度模型基础上考虑车身侧倾,建立4WS三自由度模型,简图如图2所示。

图2 三自由度模型
假设汽车纵向速度恒定不变、轮胎侧偏特性呈线性且前后轮小转角情况下,则三自由度模型的动力学方程为:
(2)
式中:m为整车质量;ms为汽车簧载质量;δf、δr分别为汽车前、后轮转角;a、b为质心至前后轴距离;u为车身纵向速度;β为质心处侧偏角;h为簧载质心到侧倾轴的距离;φ为车身侧倾角;ωr为横摆角速度;Ix为簧载绕侧倾轴的转动惯量;Iz为车身横摆转动惯量;Ixz为簧载的惯量积;
将其化为状态方程,可得:
(3)

当δr=0时,即为前轮转向汽车。
1.3 轮胎模型
轮胎力学特性是汽车操纵动力学研究的一个重点[5],且轮胎很大程度上决定了整车的动力学特性,在操纵稳定性和安全性等方面都有很重要的影响。在多种轮胎模型中,魔术公式模型采用同一公式即可表达轮胎的各项力学特性,具有拟合精度高的优点因此,本文采用魔术公式轮胎模型进行模型的搭建[6],其形式如下。
Y(x)=
Dsin[Carctan{Bx-E(Bx-arctan(Bx))}]
(4)
式中:Y(x)为侧向力、纵向力、回正力矩;x为相应的侧偏角或纵向滑移率;B、C、D依次由轮胎的垂直载荷和外倾角来确定。
根据魔术公式在Simulink中搭建轮胎的侧向力学模型,如图2所示。
由上述模型可得到轮胎的侧向力学特性,如图4所示。
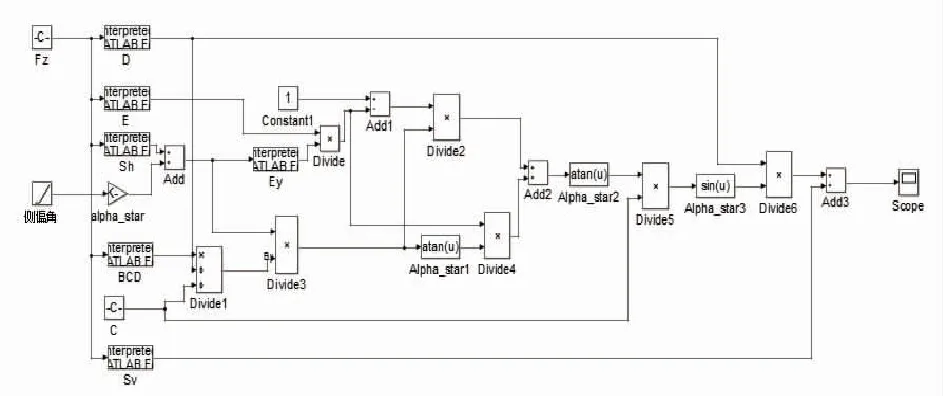
图3 魔术公式轮胎模型
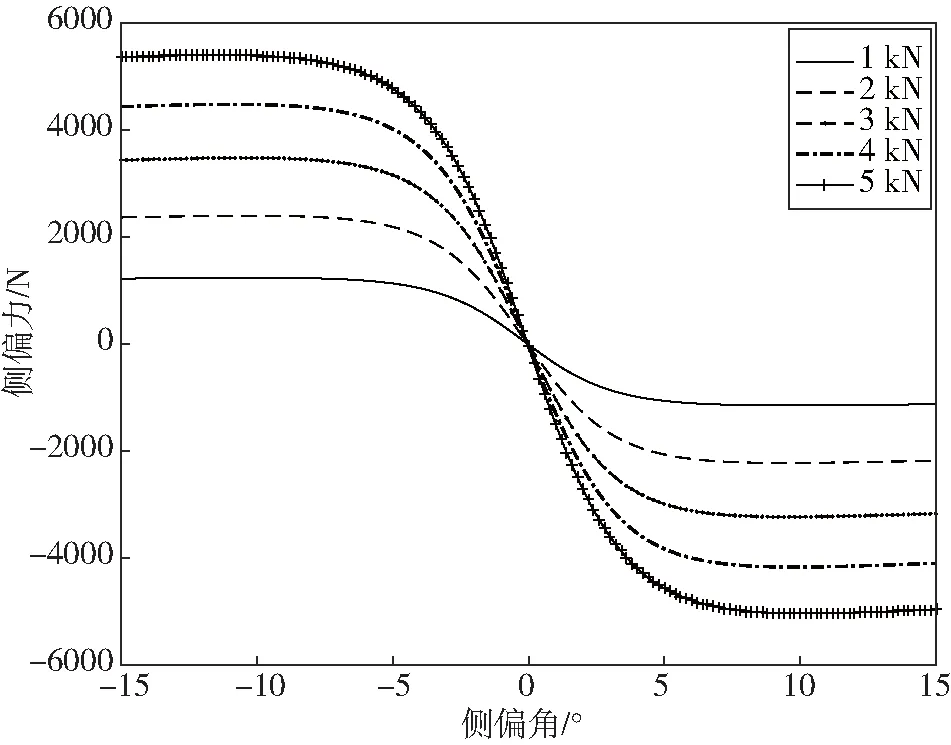
图4 魔术公式轮胎侧向力学特性
由图3可知,当侧偏角在4°以内时,轮胎的侧偏特性呈线性关系,随着侧偏角越来越大,斜率逐渐变小,直至为零。此时,侧偏力达到一个稳定值。
2 三自由度4WS非线性模型
四轮转向车辆是相对较复杂的非线性系统,其非线性主要体现在轮胎上[7],所以模型的建立共分为轮胎模块和车辆模块。结合之前建立的三自由度模型和轮胎模型,搭建三自由度非线性模型,如图5所示。

图5 四轮转向车辆三自由度非线性模型
3 4WS汽车操纵稳定性分析
操纵稳定性是汽车最重要的性能之一,关乎汽车的品质和安全,在产品开发的过程中占据着重要地位。本文采用Sano[8]提出的前轮比例控制作为4WS汽车的控制算法,如式5所示。通过阶跃仿真试验对比分析模型的转向特性。
(5)
取前轮转角输入为0.1 rad,起跃时间为0.1 s,车速分别为5 m/s和20 m/s.以前轮转向二自由度线性模型、4WS二自由度线性模型和4WS三自由度非线性模型作为研究对象,进行阶跃仿真试验。仿真结果如图6、图7所示。

图6 质心侧偏角响应

图7 横摆角速度响应
由图6可知,四轮转向汽车的质心侧偏角明显减小,提高了车辆的循迹能力,且瞬态响应变化相对较小,可以有效的避免侧翻,甩尾等危险事故的发生。其中,相较于非线性三自由度模型来说,线性二自由度的质心侧偏角稳态值更接近零值,控制效果更好。这是由于在以质心侧偏角为零的条件下推导前后轮比例关系时,并没有考虑轮胎的非线性和车身的侧倾,因此对于非线性三自由度模型的控制效果较差,应当在充分考虑轮胎非线性特性和车身侧倾的情况下选取合适的非线性控制算法进行控制。
由图7可知,在低速时,四轮转向汽车横摆角速度明显增大,提高了车辆的机动性。而在高速时则恰恰相反,降低了横摆角速度稳态值,提高了汽车的稳定性和安全性。其中非线性三自由度模型相较于线性二自由度模型可以更快的达到稳态,响应时间较短。
4 结论
传统的四轮转向汽车操纵稳定性研究都是基于二自由度模型进行研究,没有考虑非线性特性的影响。本文在传统二自由度线性模型基础上,考虑了侧倾和轮胎侧偏特性的影响,搭建完成了三自由度非线性模型。使汽车的运行情况更加接近于真实道路行驶状况,有利于更好地分析四轮转向汽车操纵稳定性。
对前轮转向模型、线性二自由度模型、非线性三自由度模型分别进行阶跃仿真实验,不同的速度条件下,分别完成横摆角速度响应和质心侧偏角响应试验,对比分析二自由度线性模型和三自由度非线性模型的操纵稳定性。通过仿真分析可知,两者的转向特性相差不大,但在考虑到轮胎的非线性和车身的侧倾下,非线性三自由度模型具有更好效果,使得四轮转向汽车横摆角速度明显增大,质心侧偏角明显减小,可以有效避免侧翻、甩尾等危险行驶状况,显著提高了汽车的机动性和循迹能力,提高了汽车的稳定性和安全性。

