风力发电并网运行风险评估
韩 帅,刘立群,张文超
(太原科技大学电子信息工程学院,太原 030024)
风力发电作为多微网的主要组成单元,与多个分布式电源、储能装置、相关负荷和监控、保护装置汇集而成的多微网协调发电系统,是一个能够按照目标,实现自我控制、保护和管理的自治供电系统。目前,交直流混合微电网系统结构示意图如图1所示:
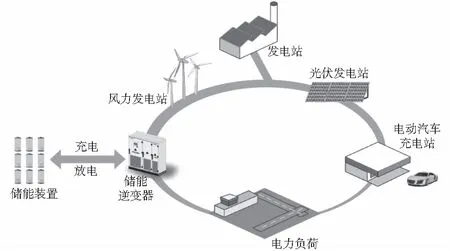
图1 交直流混合微电网系统结构示意图
风力发电系统作为新型电力系统的组成部分,电网结构复杂,为保障供电的可靠性,需针对风力发电系统进行并网运行风险因素评估和逆变器控制的研究。加强多微网系统风险因素评估,从源头做好预警机制,利用机器学习对风力发电系统稳定运行的风险因素进行合理分析,分析影响系统稳定运行的重要因素,并结合数据获得有价值的量化数据,进而实现对系统运行状态的预判和决策。
对风力发电系统提前进行运行策略和网架结构调整,使系统更安全可靠地运行,为实现风力发电系统自愈提供技术理论支撑。我国目前对于风力发电并网运行的风险因素评估理论已具有一定突破:国内诸多学者由大电网的风险因素评估方法,形成对风力发电系统运行风险因素的分析。影响因素包括:风力发电等分布式电源的功率不确定性、负荷随机性、电网网络结构的复杂性、以及保护和设备故障的不确定性、自然灾害的因素以及一些偶然的人为因素等[1]。从风力发电系统风险因素评估所考虑的因素出发,现已有的评估方法确定性方法,是假定系统可能发生的故障,在每个故障下分析系统是否出现运行条件的越限,如N-1静态安全分析等[2]。概率分析建立配电网风险指标评估,同时运用了CIME语言及状态枚举算法,计算出风险大小[3]。
本文研究思路与主要工作:当前,对风力发电并网风险评估主要利用:随机抽取样本的技术,即蒙特卡洛法对随机潮流进行评估,但是随着分布式发电的集成化,对于大型的复杂系统,该方法运算量就会大大地增加,对计算的设备性能就会有所要求,对应的投资也会增大,不利于经济性。本文采用半不变量算法,对风力发电系统进行随机建模,主要包括微网系统中的分布式风力发电原件以及投入负荷的随机模型;分析建立系统各节点电压越限、支路潮流越限的计算概率和严重度指标方法。并以此来评估风力发电并网运行后给系统带来的随机风险。分析风力发电构成的微电网并网运行容量的不同、对系统所造成的电压越限风险和支路潮流越限风险,并定量评估其对应的风险数值大小。并以蒙特卡洛法为参考,验证本方法的有效性。
1 风力发电并网运行的风险
1.1 风险定义及特性
社会发展与进步,风险客观存在,造成损失的概率大小随生产力不断进步在持续改变。对其分析和研究有着不同的途径和方法,其定义也不尽相同。不确定性对目标的影响是ISO31000国际标准化组织对“风险”的定义。事件发生的概率和产生的后果这两个基本要素用来衡量风险的大小。系统中电力负荷的不确定性、设备的随机故障导致对系统运行准确预测难以实现。通过对辨识系统失效事件发生的可能性进行电力系统的风险评估,用来分析不同工况下系统各种指标越限的严重程度。
风险所具有的主要特点包括:
(1)客观性:风险的存在是客观的,不受主观意志而发生改变。
(2)普遍性:风险存在社会生产和生活方方面面。
(3)偶然性:不同风险的发生可能性有所不同,其发生具有随机性和不可预估的特点。
(4)必然性:当风险值达到一定程度时,其发生的概率达到100%.
(5)可控性:通过改变系统中的受控变量,可对风险的大小进行控制。
1.2 风力发电并网运行面临的风险
多微网中的风力发电并网可以提高大电网的弹性,改变网络结构以及潮流分布,提高能量的利用率。但是也必须综合考虑其对整个电力系统产生的负面影响[4]。风力发电并网运行将使电力系统的结构和运行状态发生很大的改变。
微电网中风力发电属于间歇型发电,其输出功率具有随机性,当电力系统中的负荷发生波动时,这将会给电力系统的稳定运行带来一定的风险。
2 随机潮流算法
2.1 半不变量
半不变量是将分布函数F(x)的特征函数进行相关数学变换而得到的变量,也是随机变量的一种数字特征,可以由不高于相应阶次的各阶距求得,随机变量特征函数的表达式如下[5]:

(1)
对特征函数取自然对数,按照麦克劳林展级数式展开,可得:
(2)
式中kr为r阶半不变量,s表示展开表达式的项数,o(ts)表示余项的无穷小量。半不变量的求取过程主要由距来求取,通常前7阶半不变量与中心矩Mv的有如下关系:
(3)
随机变量的1阶半不变量是它的数学期望,其2阶半不变量对应的是其数学方差。当服从正态分布的随机变量,该随机变量≥3阶的半不变量都为0.
常用的关于半不变量的两个性质:

(4)
性质2:随机变量n倍的v阶半不变量等于该变量的v阶半不变量的nv倍。
2.2 利用半不变量的解析过程
对系统的输入功率进行潮流计算,对应的系统各支路中功率变化量满足相互独立的随机变量,通过对其进行卷积运算,就可以获得各注入功率所满足的分布函数。将该分布函数用半不变量法化为线性。在实际工程中,由于采用节点功率作为节点注入量,这会造成电力系统潮流方程呈非线性化,在求解过程中需要把非线性方程式(组)转变为对相应线性方程式(组)求解的过程,即逐次线性化过程。对于计算系统支路潮流时,已知各节点的状态变量可以利用如下公式来进行计算:
Pij=-UiUj(Gijcosθ+Bijsinθij)+tijGijUi2
(5)
Qij=-UiUj(Gijsinθij-Bijcosθij)+(Bij-bij0)Ui2
(6)
式中:tij为对应支路上的变压比,bij0对应的是1/2线路导纳。
将上式用随机变量表示出来可得:
Sz=fz(X)
(7)
式中:Sz表示支路上的输入功率,fz(.)表示支路上的状态变量与输入功率之间的对应关系。其中Sz,X都为随机变量。将该式进行线性化处理,利用泰勒级数展开式将其展开,可得:
Sz=Sz0+ΔSz=fz(X0)+G0ΔX+…
(8)
式中:Sz0为潮流计算过程中的期望值,ΔSz实际功率与期望功率之间的波动量。G0反映了支路功率在状态量的期望值附近的变化情况。即:
(9)
整理(8)式,忽略式中二阶以上的高次项,可得输入功率在各支路的分布情况,如下:
(10)
式中:T0反映了输入功率发生变化时对各支路功率的影响。
风力发电并网运行系统中不确定性的原因,是由各节点注入功率S的随机变化量ΔS产生,该随机变化量主要由:负荷的随机变化量ΔSload、分布式电源出力的随机性等构成(主要包括:风力发电的随机变量ΔSwind),将这几个独立随机变量进行卷积计算可得到如下公式:
ΔS=ΔSload⊕ΔSwind
(11)
利用半不变量的性质将上述公式进行变换,这几个随机变量对应半不变量分别为:节点注入功率变化量ΔS(k),负荷引起功率变化量ΔSload(k),风力发电引起系统功率变化ΔSwind(k).对应的这几个半不变量满足式(12):
ΔS(k)=ΔSload(k)+ΔSwind(k)
(12)
同样利用半不变量性质对状态变量的变化量和支路功率的变化量进行简单换算,以简化其卷积计算,对应的公式为:
Z(k)=(T0)k×ΔS(k)
(13)
变量节点状态变量ΔX(k)和支路功率的k阶半不变量ΔSz(k);(J0-1)(k)、(T0)(k)为对应的不同阶次的灵敏度矩阵。
2.3 随机变量概率分布的求取
求取随机变量概率分布的函数值,通过求取该随机变量各阶半不变量,并结合级数展开式拟合出所要求取的随机变量的概率分布函数情况。
首先将随机变量标准化:
(14)
(15)
Cornish-Fisher级数在计算非正态概率分布时,具有较高的精确度。令连续随机变量X的均值和方差分别为和,则其标准形式即为:
ε=(x-μ)/σ
(16)
Cornish-Fisher级数展开对应的概率密度函数如下:
(17)
3 风力发电并网运行的风险评估
3.1 风力发电的随机模型
风机能否正常工作及外界风速的大小,都会在不同程度上影响风力发电系统的输出功率。风速概率分布的模拟模型主要包括:瑞利(Rayleigh)分布、韦伯(Weibull)分布、对数正态分布等。当前研究发现,实际风速模型最接近韦伯分布模型。
假设风速概率分布服从双参数韦伯分布,对应的概率密度函数与累积概率分布函数如式(18):
(18)
式中:v表示风速;c表示韦伯分布中的函数尺度参数;k则表示函数的形状参数。
以上公式可得:形状参数取值k=1,原韦伯分布函数与指数分布函数相同;
形状参数取值k=2,对应的韦伯分布函数与瑞利(Rayleigh)分布函数相同。
韦伯分布函数对应参数,可以用实际统计的平均风速值μ和标准差大小σ来做近似计算,如式(19):
(19)
式中,Γ(x)表示Gamma函数又称欧拉第二积分,其计算公式满足式(20):

(20)
韦伯分布的均值和方差分别为:
(21)
从上式可以看出,输出功率的概率密度分布函数也服从Beta分布,其v阶原点矩如(22):
αv=

(22)
3.2 系统节点电压越限的风险指标函数
系统电压降低,会使系统的能量损耗和功率损耗增加,并对系统稳定运行造成一定的影响,增加投资,使经济性变差。因此需要建立电压的风险指标。
节点电压越限的概率计算公式如下:
(23)
以电压偏移量作为影响电力系统发生事故严重性对应的后果函数值,即节点电压的越限严重度指标,如下公式:
场地全部钻孔(CK1~CK10,ZK1~ZK21)均有揭露,揭露层厚 1.30~4.50m,平均厚度2.66m;层顶高程3.40~3.83m,层顶深度0.00~0.00m。
(24)
(25)
式中:Vi表示电压在系统网络节点i上的幅值大小;Vimin,Vimax为系统节点i所允许的最值情况,本文令最值为额定值的±5%VN,用F(V)表示其累积分布函数。
则电压越限的风险指标函数可以表示如下:
(26)
3.3 支路潮流越限的风险指标函数
当系统处于正常工况下,支路潮流使系统失稳的概率很小;但是,系统处于非正常运行状态时,会使支路潮流增加,当其数值达到线路承受最大值时,会引发线路上的继保装置发生动作,所以需要使其控制在正常工作范围以内,以降低线路跳闸的概率性。因此,研究多微网并网运行系统的风险评估需要考虑到系统网络支路的潮流问题,设置对应的支路潮流行为评估的指标函数。
支路潮流行为的概率运算,仅以最大值进行计算,对应的计算公式如下:
Pr(Sij)=Pr(Sij>Sijmax)=1-F(Sijmax)
(27)
支路过负荷的严峻程度可以用公式(28)表示:
(28)
式中:Sij对应的是支路ij上的有功潮流,Sijmax对应的是有功潮流所允许的上限值大小,当之路上带负荷为其最大有功容量时,该容量的大小值设定为期望的容量值1.3倍。
F(Sij)用来表示支路中的潮流计算时,计算结果所对应的累积分布情况。
Rs=Pr(Sij)Sev(Sij)
(29)
4 风力发电并网运行风险评估流程
评估流程如下:
第一步:采集多微网并网运行时系统随机潮流计算所需的原始数据,对该数据做出进行检测,并得到需要的变量,主要是:包含了进行常规潮流运算时,系统运行状态所需的参数在内,还包括有网络系统的各节点有关信息内容,以及系统所带的运行负荷对应的统计模型的数字特征、风电发电、太阳能发电的输出功率及概率分布数据。
第二步:由以上所推到出概率模型的表达式,来对负荷、风电模型的半不变量进行求取。利用半不变量的性质,将对求取的结果进行线性叠加,以此得到系统网络各节点发力时的半不变量数值大小。
第三步:利用牛拉法对系统的各支路进行潮流运算,得到对应系统各节点处的电压的期望值大小,以及系统的各支路潮流发力所对应的期望大小,由潮流计算最终迭代结果的雅克比矩阵J0,可以求出系统各支路对应的灵敏度矩阵T0.
第四步:对系统的各节点电压、支路潮流,利用概率统计相关知识,求取其对应的半不变量,将结果用级数展开,得到网络系统中不同的节点电压以及网络系统的支路潮流所对应的概率密度和累积分布函数的表达式对应的曲线。
第五步:由概率分布情况,对运行系统的节点电压和支路潮流功率在运行过程中,将会出现的一系列行为指标做出相应的评估。
5 算例分析
以文献[7]提供的标准IEEE33节点网络系统为基础,在该节点网络系统上并入多微网系统,用来进行了风力发电并网运行风险因素评估的研究。该网络系统接线图如图2所示;

图2 网络系统接线图
该系统基准容量Sb=1 MVA,其基准电压为Vb=24.9 kV,节点参考电压为1.03的基准电压Vroot=1.03 p.u.=25.647 kV,为计算简便化,系统中所有的输电线路都被简化为单相线路,并且将24.9/4.16 kV变压器简化,忽略电压调整器在系统中的作用,将系统用一个电压等级来表示。
假设风力发电机模型参数选为:
单机额定容量为50 kW;
切入风速:vci=3 m/s;
额定风速:vr=13.5 m/s;
切出风速:vco=20 m/s.
将容量分别为300 kW、600 kW、800 kW和1.1 MW的风机,并入网络系统的33节点处,计算系统其余各节点的电压越限概率、严重度和风险大小,结果如下图所示:
图3a、3b、3c、3d、3e、3f是风机接在33节点时,对比接入容量的不同,所对应的系统各节点电压越限概率、电压越限严重度和风险大小也有所不同。
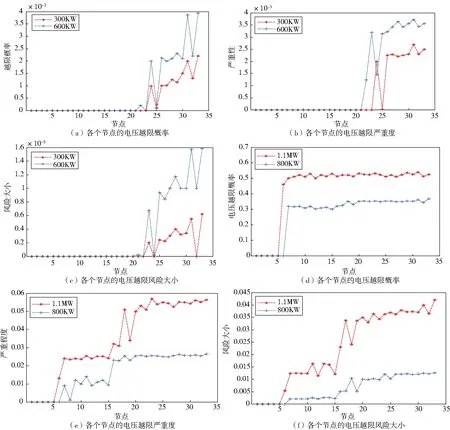
图3 各节点的电压越限概率、严重度和风险大小
可以得出结论:随着风机容量的増大,同一节点的电压越限概率、严重度与风机接入的容量成正比关系。
由图3c、3f 可以看出,将不同容量的风力发电机组接入节点33处后,随着接入风机容量的不断增大,系统的电压越限风险指标与其呈现正比关系。
由此可以得出结论:同一节点处,接入系统的风力发电容量越大,对应系统的安全风险也会呈现上升趋势。
当风机接入容量为300 kW、600 kW时,节点1~21的越限的风险值几乎为零;但是接入额定容量分别增加到750 kW、1.1 kW时,仅仅节点1~5的越限的风险值为几乎为零。
由此可以说明:增大风力发电的并入容量,网络系统中有越限风险的节点数也随之呈现正相关趋势,并且每个节点行为风险大小也有所不同——距离接入节点越近,对应的电压越限风险就越大。
6 结论
本文对风力发电并网运行进行风险评估,确定风力发电的随机概率模型,对比风力发力状况与接入不同容量时的工作状况:探究对系统的风险指标。
得到如下结论:在同一情况下,不同节点的有功负荷不同,对应节点的电压、支路潮流越限风险大小不同。负荷正态分布模型中期望与标准差会影响节点风险值的大小。负荷标准差越大,系统节点电压越限、支路潮流越限可能性就会增加。
不同容量的分布式电源接入都会系统的节点电压、支路潮流行为带来一定影响。光伏发电对系统节点电压、支路潮流行为带来一定的影响,通过定量计算出不同情况下风险指标。可以看出:随着接入容量的増加,系统的电压越限风险指标与之呈正相关趋势;电气距离与节点电压越限风险呈负相关趋势。接入容量与支路潮流过载风险的呈正相关趋势;电气距离与支路潮流过载风险呈负相关趋势。
本文对风力发电并网运行进行风险评估,确定多微网并网运行的风力发电的随机概率模型时,没有考虑天气等因素,而微电网中的风力发电受天气等因素的影响。因此,若将天气等因素加入其输出功率模型中,会使模型更加符合实际。同时,连续型负荷模型对应的是采用正态分布模型,当然也可以在该模型上进一步地探究完善。同时,在探究不同容量的风力发电并网运行时,尚未探究不同的接入点对于同一系统的风险评估的影响以及风力发电从多个接入点并网运行时该风险评估方法的适用性;利用随机潮流法对系统进行风险评估时,未考虑系统在实际运行中,对应的随机变量之间都存在一定的耦合关系,本文以相互独立变量进行分析,故该方法与真实情况必然有一定的出入,故该算法还可以进一步完善。

