车用双向筒式液压减振器阻尼孔阻尼特性分析

盛湘飞，赵科宇，李 智，戴 权，汪迅辉

（1.南华大学 机械工程学院，湖南 衡阳421001；2.南华大学 土木工程学院，湖南 衡阳421001；3.南华大学 创新创业学院，湖南 衡阳421001）

减振器是汽车悬架系统的重要组成部分，其可在车架与车桥有相对运动时产生阻尼力，加快整车振幅的衰减速度，能有效提高整车行驶时的平顺性和操纵稳定性[1-2]。目前，因双向筒式液压减振器具有结构简单、工作可靠和性价比高等优点，已在汽车行业得到广泛应用[3-5]。

影响双向筒式液压减振器阻尼力的因素有车架与车桥间的相对运动速度、油液黏度、阻尼孔几何特征参数等[6-7]。减振器工作时，车架与车桥间的相对运动最终转变为减振器活塞与缸筒间的相对运动，并视为减振器输入。减振器在不同的输入条件下，油液黏度及阻尼孔几何特征参数对减振器阻尼特性均有影响。近年来，国内外研究人员对液压减振器的阻尼特性进行了一些研究，Wang 等[8]、Alireza等[9]、Kate等[10]和段福斌等[11]分别建立了单筒式液压减振器的理论分析模型，分析了减振器串联刚度、垫片叠加方式、内泄漏、阻尼阀片卡滞、油液黏度退化对阻尼特性的影响。然而，现有理论研究大多是基于减振器内特性的经验或半经验模型，计算难度大，精度低。随着计算机和有限元模拟技术的发展，愈来愈多的研究人员尝试采用模拟或模拟与试验相结合的研究方法对减振器阻尼特性进行探索，于振环等[12]基于流-固耦合动力学模型，获得了减振器阻尼力与活塞运动速度的变化曲线；庄晔等[13]和赵雷雷等[14]借助有限元工具分析了节流阀片开度对阻尼力的影响。

通过梳理与减振器阻尼特性相关的研究工作不难发现，虽然对影响减振器阻尼特性的因素开展的研究较多，但是未充分考虑因素间相互作用对减振器阻尼特性的影响，而这恰恰是精确设计减振器阻尼孔和合理匹配减振器减振效果的关键。本文将采用数值模拟与正交试验设计、方差分析和单因素分析相结合的研究方法，探索在不同输入条件下阻尼孔几何特征参数及油液黏度对双向筒式液压减振器阻尼孔阻尼特性的影响规律，研究成果可为减振器结构设计及其参数调整提供理论指导，以进一步改善其减振效果。

1 建立有限元分析模型

因Fluent软件包含丰富的且经工程验证过的物理模型，采用了多种求解方法和多重网格加速收敛技术，可以用来模拟从不可压缩到高超音速范围内的各种复杂流场，故本文采用ANSYS Workbench中的Fluent模块对减振器阻尼孔的阻尼特性进行分析。

1.1 减振器阻尼孔几何模型

双向筒式液压减振器内部结构较为复杂，而影响减振器阻尼特性并与阻尼孔几何特征相关联的参数主要有阀片厚度、阀片数量、阀片开度及缸筒直径等。本文对减振器几何模型进行了简化，分别用阻尼孔直径d和阻尼孔长度l来表征阀片厚度、阀片数量及阀片开度等信息，如图1所示。并根据常用液压减振器缸筒内径D及壁厚t的尺寸，取D=30 mm，t=3 mm，d和l的取值如表1所示。

图1 简化后的液压减振器阻尼孔几何模型

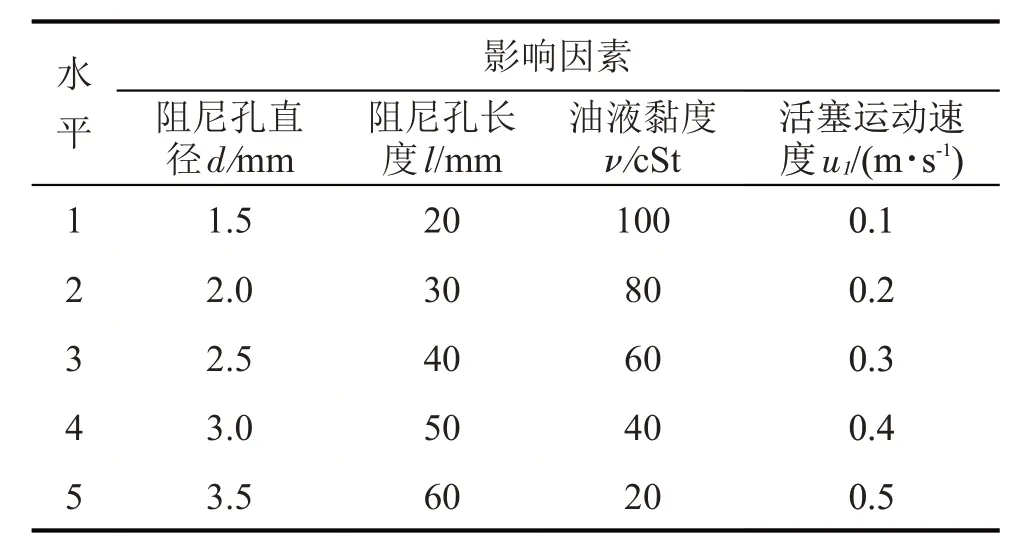
表1 正交试验用参数及其水平

1.2 边界条件与网格划分

考虑到减振器缸筒与活塞在工作时均不发生塑性变形或变形量较小且具有规则的回转体几何特征，故将缸筒和活塞设置为刚体，并使用对称模型对其建模。另外，减振器在工作时，活塞相对于缸筒进行往复直线运动，在运动过程中，缸筒内的油液经活塞阻尼孔在左右两腔间流动，流动时产生的阻尼力主要来自活塞阻尼孔，为实现这一运动过程，本文在模型左端面对油液施加了一定流速，出口边界条件设置为压力出口（标准大气压）。网格划分时，对阻尼孔及其周边区域的网格进行了细化（非加密区单元尺寸为0.5 mm，加密区单元尺寸为0.07 mm），并使用自适应网格，划分后的网格数为1 112 185，结果如图2所示。

1.3 其他

模拟时使用的油液为硅油（Silicon-liquid），其密度ρ为900 kg/m3，由于油液在不同工况条件下的流动状态不同（包括层流和紊流），模拟前首先根据式（1）计算各工况条件下的雷诺数，结果如表2所示，油液在左腔的流动状态均为层流，流经阻尼孔时的流动状态与阻尼孔直径和活塞运动速度有关，流态相对复杂。本文根据油液的流动状态分别选择不同的状态模型（层流为laminar模型，紊流为标准k-ε模型），并选用simple算法（该算法适合任何流速的流动）对减振器阻尼特性进行模拟运算。

式中：Re为雷诺数；u为平均流速；R为水力半径；ν为油液的运动黏度。

图2 液压减振器阻尼孔网格模型

2 模拟结果与分析

2.1 模拟方案

通过查阅大量参考文献可知，影响减振器阻尼孔阻尼力的因数较多，若仅采用传统的单因素分析法，将导致试验次数过多，工作量过大。本文拟采用正交试验设计方法，用有限的试验次数探索各因素及其水平对试验结果的影响。试验选用的因数及其水平如表1所示，其中阻尼孔直径、阻尼孔长度、油液黏度和活塞运动速度分别用符号I、II、III 和IV表示。

根据试验因素数量及其取值水平，选择L25（56）正交表安排试验，各试验所用因素组合如表2所示。

2.2 模拟结果

采用已建立的减振器有限元模型，并根据表2给出的参数，对减振器内部油液通过阻尼孔时的流动过程进行模拟，结果如图3所示。可见，当油液以一定速度自左向右流经阻尼孔时，左腔油液经阻尼孔流至右腔时要克服阻尼孔的沿程压力损失Δp1（见式（2））和因截面突变所产生的局部压力损失Δp2（见式（3），影响液压元件局部压力损失的因素较多，不同几何模型和流动状态对应的局部压力损失均不相同，准确计算该压力损失难度较大），依据流体力学理论可知，油液流经阻尼孔的进出口压差Δp=p左-p右，右腔相对压力p右=0，即p左=Δp=Δp1+Δp2，故左腔油液压力随油液自左向右流动逐渐升高，并最终趋于稳定；油液在阻尼孔内部流动时只需克服沿程压力损失，在其他参数不变的情况下，阻尼孔内部的油液压力与阻尼孔长度有关，长度越长，压力损失越大，故阻尼孔内部油液压力自左向右呈明显梯度分布。

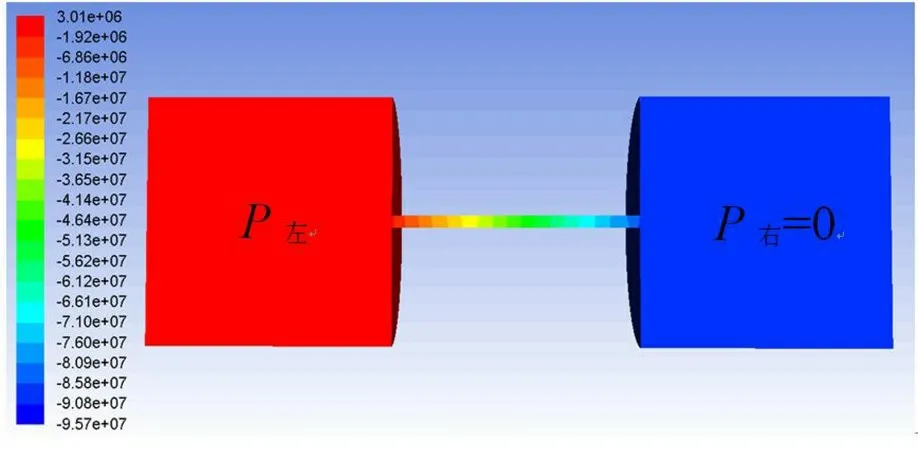
图3 液压减振器阻尼孔阻尼特性的模拟结果

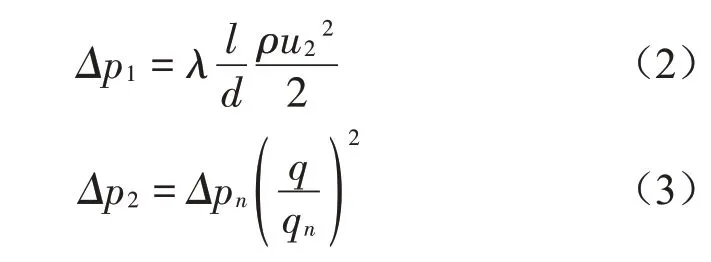
式中：Δp1为阻尼孔沿程压力损失；λ为沿程阻力系数（层流时紊流时λ主要与雷诺数和管壁的相对粗糙度相关）；u2为油液流经阻尼孔时的平均流速；Δp2为局部压力损失；qn为额定流量；Δpn为在额定流量下的压力损失；q为实际流量。

对于减振器而言，阻尼孔的作用是增加油液从左腔向右腔流动时的压力，从而增加减振器缸筒与活塞相对运动时的阻力，并通过将振动能量转变为油液间的内摩擦热以及油液与阻尼孔内壁间的摩擦热，起到衰减整车振幅的作用，故可用模拟过程中油液通过阻尼孔时于左腔形成的最大压力值Pmax来表征阻尼孔的阻尼力。

2.3 方差分析

借助Fluent 后处理模块，提取25组有限元模拟结果中减振器缸筒内的最大压力值Pmax，并对正交试验结果进行方差分析，结果如表3所示。表中S为偏差平方和，其中各因素的偏差平方和用Sj表示，误差项偏差平方和用Se表示；f为自由度，其中各因素的自由度用fj表示，误差项的自由度用fe表示。定义统计量：

根据F检验可知，若Fj＞F1-α(fj,fe)，即在给定显著水平α条件下，该因素对目标结果有显著影响。经查表可知：当α=0.05时，F0.95(4,8)=3.84（若Fj≥3.84，即高度显著）；当α=0.1时，F0.9(4,8)=2.81（若2.81≤Fj＜3.84，即显著），否则不显著。

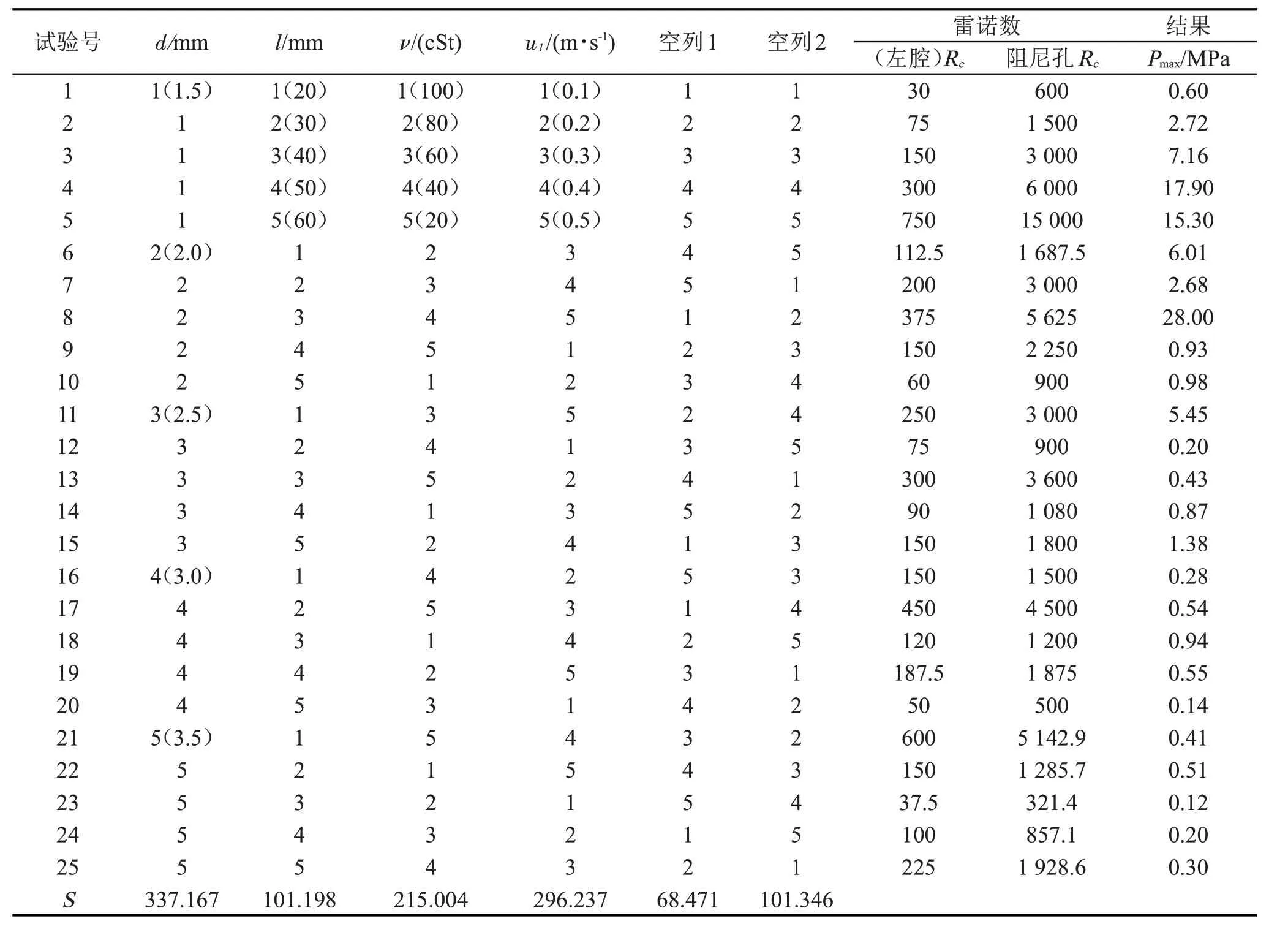
表2 正交试验用因素组合及结果

表3 正交试验的方差分析结果

根据表3的分析结果可知，阻尼孔直径与活塞运动速度对油液流经阻尼孔时的阻尼力有显著影响，各因素对阻尼力影响的主次顺序依次为阻尼孔直径、活塞运动速度、油液黏度、阻尼孔长度。

2.4 单因素分析

因阻尼孔长度和油液黏度对阻尼力影响不如阻尼孔直径和活塞运动速度显著，故在后续分析中未考虑阻尼孔长度和油液黏度变化对阻尼力的影响。文中采用单因素分析法进一步探索阻尼力随减振器阻尼孔直径和活塞运动速度的变化规律，结果如图4和图5所示。在给定参数条件下，阻尼力随阻尼孔直径增加而减小（如图4所示），随活塞运动速度增加而增加（如图5所示），表明减振器工作时阻尼孔直径越小，活塞运动速度越快，所产生的阻尼力越大。采用Allometric1函数对图中数据点进行非线性拟合，可见图4和图5中各曲线斜率的变化趋势总体上随活塞运动速度增加或阻尼孔直径减小而增加，表明活塞运动速度越快，阻尼孔直径越小，两者对阻尼力的影响越显著，减振器振幅衰减速度越快。

油液流经阻尼孔时流层间的内摩擦力作用是液压减振器工作时产生阻尼力的主要原因（如式（5）所示），内摩擦力越大，阻尼孔入口处所产生的阻尼力也就越大。由式（5）可知，在油液黏度和流层接触面积不变的情况下，内摩擦力与速度梯度呈正比关系。当阻尼孔直径变小或活塞运动速度加快时，均会使油液通过阻尼孔时的流速增加，流速越快，阻尼孔内部不同流层间的速度梯度越大，即阻尼力与油液流动速度亦呈线性关系。

式中：Ff为内摩擦力；μ=ρν为动力黏度；A为流层接触面积为速度梯度。

对图4和图5中阻尼力的变化规律进行分析。图4中对应的阻尼孔直径变化会引起油液流经阻尼孔时的速度发生非线性变化，根据连续性方程可知，油液流经减振器左腔的流速与通流面积之乘积应等于流经阻尼孔时的流速与通流面积之乘积，即有：可见，在图4中各曲线在取对应参数条件下速度梯度与阻尼孔直径的平方呈反比，阻尼力的变化幅值随阻尼孔直径的增加而降低，与图中所示各曲线一致；图5中各曲线对应参数不存在阻尼孔直径变化的情况，若仅考虑内摩擦力对阻尼力的影响，阻尼力与活塞运动速度应呈线性变化关系，这与图中所示曲线3、4和5的变化规律不一致，表明除流层间的内摩擦力以外，还有其他因素影响阻尼力。故此，文中计算了图4和图5对应工艺参数条件下的雷诺数，结果如图6和图7所示。当阻尼孔直径较小且活塞运动速度较快时，对应雷诺数将超过2 300，此时油液流动状态开始发生变化，由层流逐渐向紊流过渡。由于层流时流束状态稳定，油液质点没有横向脉动，不引起油液质点间的混杂；紊流时油液质点存在横向脉动，导致流层间质点的相互错杂交换，流束间存在干扰，并引起油液沿阻尼孔轴线方向流动的附加阻力。从图6所示的结果来看，由于雷诺数对4种曲线变化趋势的影响与内摩擦力一致，所以仅从曲线变化规律无法判定雷诺数对阻尼力是否产生影响；从图7与图5的对应关系不难看出，当阻尼孔直径为3.0 mm和3.5 mm时，因对应雷诺数小，流态未发生变化或变化不明显，图5中的曲线1 和2 亦基本呈线性变化，而曲线3、4和5的斜率则随雷诺数增加而明显增加，即表明油液杂乱无章的流动状态一定程度上也会对阻尼力产生影响。

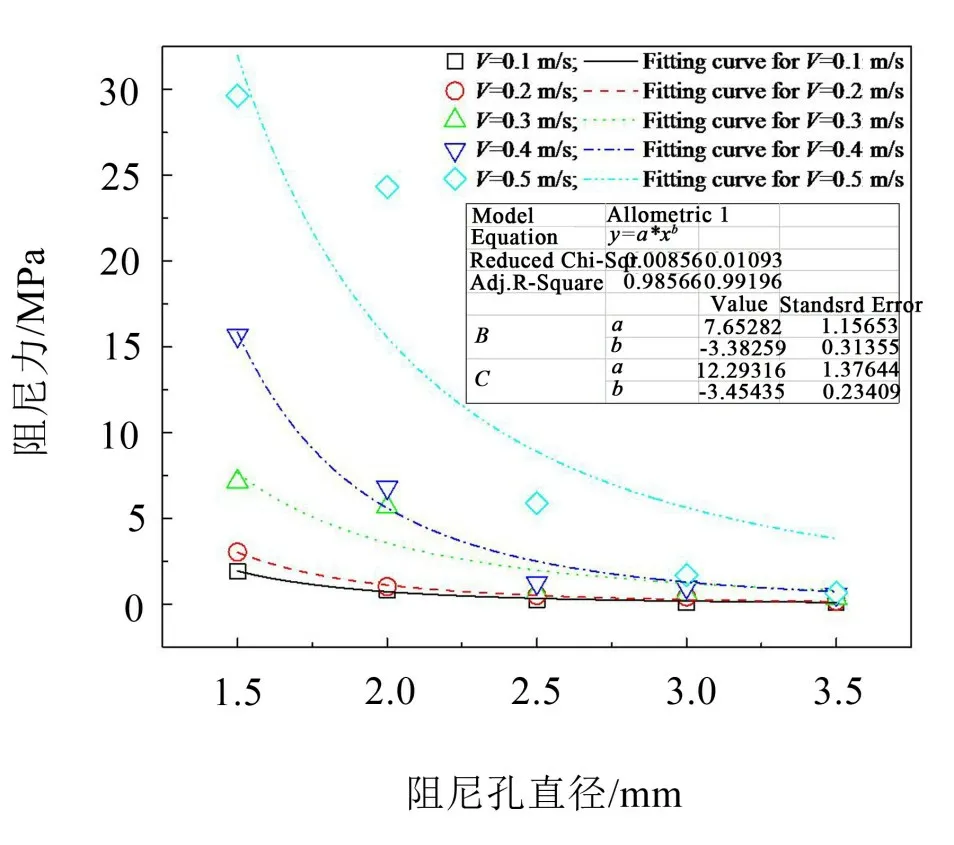
图4 阻尼力随阻尼孔直径的变化情况（l=40 mm，ν=60 cSt）

图5 阻尼力随活塞运动速度的变化情况（l=40 mm，ν=60 cSt）

图6 雷诺数随阻尼孔直径的变化情况

另外，本文对减振器在不同阻尼孔直径和活塞运动速度条件下的阻尼力调整范围进行了分析，结果如图8和图9所示。

可见，阻尼力随活塞运动速度变化而调整的范围随阻尼孔直径的增加而收窄，对数据进行非线性拟合，结果进一步表明，随阻尼孔直径的增加，阻尼力调整范围下降幅度趋于平缓，见图8；相反，阻尼力随阻尼孔直径变化而调整的范围及其增幅均随活塞运动速度的增加而增加，见图9。

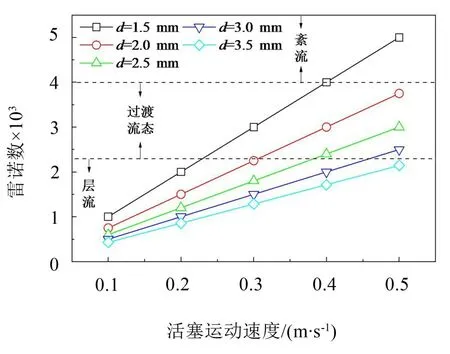
图7 雷诺数随活塞运动速度的变化情况

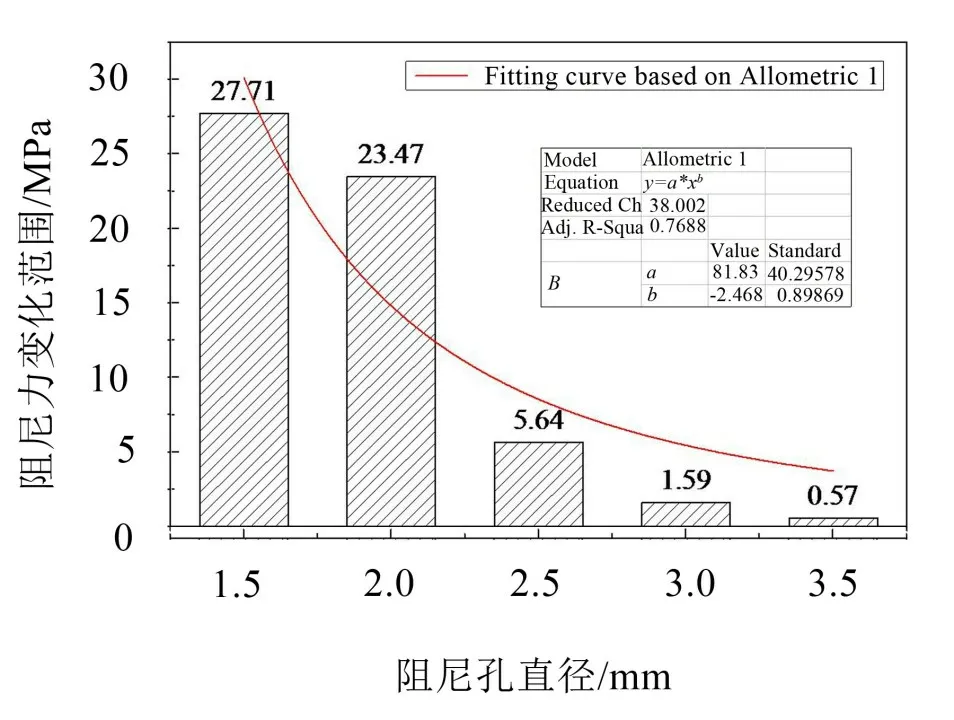
图8 阻尼力调整范围随阻尼孔直径的变化情况

图9 阻尼力调整范围随活塞运动速度的变化情况

2.5 试验验证

文献[14]借助长春试验机研究所生产的30 kN电液伺服减振器综合试验平台进行了减振器阻尼特性试验，得到了减振器阻尼力与随速度变化的曲线，结果表明，阻尼力随减振器活塞运动速度增加而增加，且增加幅度亦随之增加。本文的有限元模拟结果与文献[14]的试验结果保持一致，表明所建立的减振器阻尼特性有限元分析模型具有较高的可信度。

3 结语

研究结论如下：

(1)通过对正交试验数据进行方差分析可知，阻尼孔直径和活塞运动速度对减振器阻尼力有显著影响，而阻尼孔长度和油液黏度影响相对不显著。

(2)进一步分析减振器阻尼力的变化规律可知，在给定参数条件下，阻尼力随阻尼孔直径减小或活塞运动速度增加而增加；阻尼力的变化趋势表明，活塞运动速度越快，阻尼孔直径越小，两者对阻尼力的影响越显著，减振器振幅衰减速度越快。

(3)油液流经阻尼孔时流层间的内摩擦力是影响阻尼力大小的主要因素，研究结果亦表明，油液流动状态所引起流层间质点的相互错杂交换会对油液沿阻尼孔轴线方向流动产生附加阻力。

(4)阻尼力随活塞运动速度变化而调整的范围随阻尼孔直径的增加而收窄，且调整范围的降幅趋于平缓；阻尼力随阻尼孔直径变化而调整的范围及其增幅均随活塞运动速度的增加而增加。