考虑尾流效应的新月形覆冰四分裂输电线舞动稳定性
邹 明,刘小会,2,蔡萌琦,伍 川,叶中飞,张 博
(1.重庆交通大学 土木工程学院,重庆400074;2.重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室,重庆400074;3.成都大学 建筑与土木工程学院,成都610106;4.国网河南省电力公司 电力科学研究院,郑州450052)
在风载荷作用下覆冰输电线会发生低频大幅度的自激振动,覆冰是输电线路大幅舞动的重要因素之一,也是难以解决的问题之一。舞动发生时输电线会产生竖向的大幅振动,振幅有时会达到1 m~2 m,会导致金具的磨损和破坏、螺栓的松动和脱落、间隔棒的损坏、输电线的断裂,严重时甚至会出现输电塔倒塌,引起供电系统停运,给人们的生活和经济造成了巨大的损失[1]。
在输电线舞动研究领域,国际上广泛接受3 大舞动理论,第一个是美国学者Den Hartog 提出的单自由度垂直舞动理论[2];第二个是加拿大学者Nigol等提出的扭转舞动理论[3];第三个是日本学者Yu 等提出的偏心惯性耦合舞动理论[4]。
在3 大舞动理论的基础上,国内外的专家学者也做了大量的研究工作;例如,楼文娟等[5]基于特征值摄动法,在试验中改变横扭自振频率,提出覆冰分裂导线横扭稳定性判断条件。谢增等[6]研究了分裂导线扭转刚度的问题,提出了一种等效单导线舞动模型,用数值模拟的方法预测了输电线的舞动。严波等[7-8]通过数值模拟的方法对四分裂输电线驰振进行了数值仿真,基于静态模拟法,对覆冰四分裂导线进行了风洞模拟试验。张路飞等[9]利用有限元软件ABAQUS建立了连续档覆冰输电线模型,考察了不同档距和档数对输电线舞动的影响规律。以上4位学者主要通过数值模拟的方法对输电线的舞动进行了研究。王少华在Den Hartog舞动判断准则的基础上更加准确地推导了临界风速随风攻角的变化规律[10],在推导的过程中建立了2 自由度的模型,忽略了扭转振动。芮晓明等[11]考虑脱冰效应,研究了阻尼对舞动特性的影响。楼文娟等[12]建立了三维非线性耦合效应连续体输电线舞动动力学方程。
综上所述,现在关于导线舞动机理大多考虑了水平、竖直、扭转3个方向上舞动的耦合。目前,单导线舞动的研究较为成熟,对四分裂导线的舞动模型研究较少,但是在实际工程中,四分裂输电线更容易发生舞动,且大多数对于四分裂导线的研究没有考虑尾流效应对分裂导线的影响,这与实际工程不相符,且研究集中于数值模拟法,所得结论不具有普遍适用性。本文基于拟静态理论,建立新月形覆冰四分裂导线舞动的3 自由度振动模型,在考虑尾流效应的条件下从理论上推导了系统稳定判别式;研究了线路结构参数对新月形覆冰四分裂导线稳定性的影响,使用MATLAB软件基于稳定判别式计算出覆冰四分裂导线的临界风速。所得结果对于覆冰四分裂输电线防舞具有重要的参考价值。
1 建立力学模型
架空输电线离地面有一定的高度,地面物体对风速的影响很小,所以本文的力学舞动模型是在稳定风作用条件下建立的。由于空气尾流效应的影响,四分裂导线处于风速分布不均匀的风场中,每一根子导线受到的空气动力不同,在计算四分裂导线整体所受到的风荷载时不能用一根子导线风荷载的4倍来等效。本文考虑单档导线的舞动,假设风速沿线路方向是不发生改变的;输电线覆冰的形状和厚度沿线路方向是不变的。基于上述的假设,可以把覆冰四分裂导线舞动的复杂模型简单化,通过模态截断法就可以将连续体振动的偏微分方程转换为一个横断面沿着3个方向振动的常微分方程。分析振动稳定性的3 自由度模型如图1所示。假设稳定风从左往右流经覆冰导线,风速大小为U。导线在水平、竖直和扭转方向的约束刚度分别是Kz、Ky和Kθ。图中r是子导线中心与转动中心之间的距离,H是覆冰厚度。
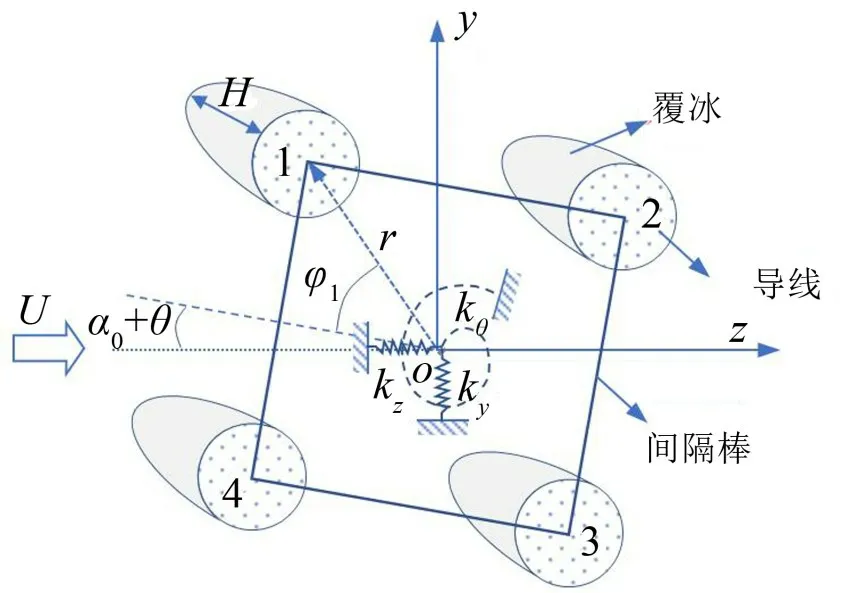
图1 覆冰四分裂导线横截面模型
其中:α0为初始风攻角;θ为动态的扭转角,随时间而改变。子导线横截面中心在整体坐标系中的坐标为
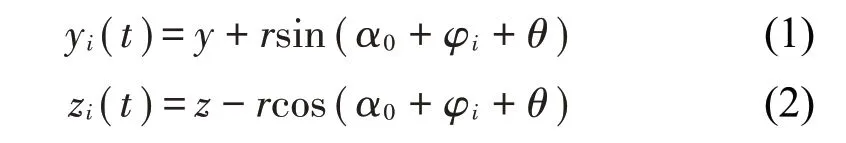
式中:y、z是四分裂导线中心在整体坐标系中的坐标值,i为导线的分裂数,i取1、2、3、4。φi是分裂导线中心和子导线中心连线与间隔棒之间的夹角,φi取值为φ1=45°;φ2=135°;φ3=225°;φ4=315°。
子导线随时间变化的位移可以表示为

式中:v、u表示四分裂导线竖直和水平方向上的位移。对子导线的位移求1阶导,得子导线的速度为

式中上标点表示对时间求导,由于在风载荷作用下导线会产生相对运动,所以导线受到的阻力FD并不是沿水平方向,而升力FL也不是沿竖向;其方向会与水平或者竖直方向形成一个夹角。本文采用拟静态假设计算覆冰四分裂导线受到的风载荷,子导线与风场之间的相对关系如图2所示。
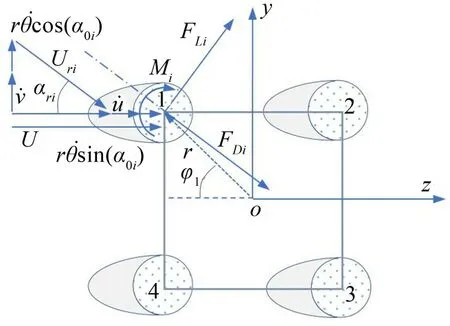
图2 基于拟静态假设的相对流场
FLi、FDi分别是子导线受到的升力和阻力;在风载荷作用下,分裂导线中心沿水平运动会产生速度,分裂导线中心的扭转运动也会产生水平向的速度分量,所以子导线在z方向的相对风速为
分裂导线中心沿竖向运动时会产生速度˙,分裂导线中心的扭转运动也会产生竖向的速度分量,所以子导线竖向的相对速度为˙+因此,实际的相对风速Uri为
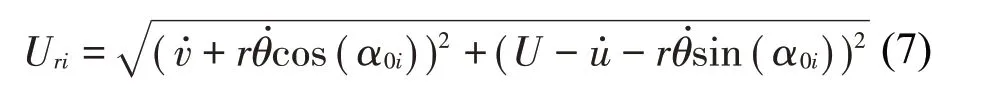
式中α0i=α0+θ+φi,子导线相对风攻角αi可以由以下式计算:
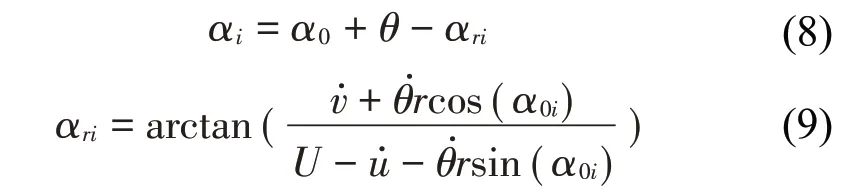
式中:αri是导线运动速度变化引起的相对风攻角改变量。覆冰子导线受到的与实际风速平行的气动阻力FDi、与实际风速垂直的升力FLi和扭转力矩Mi可以通过以下公式得到:
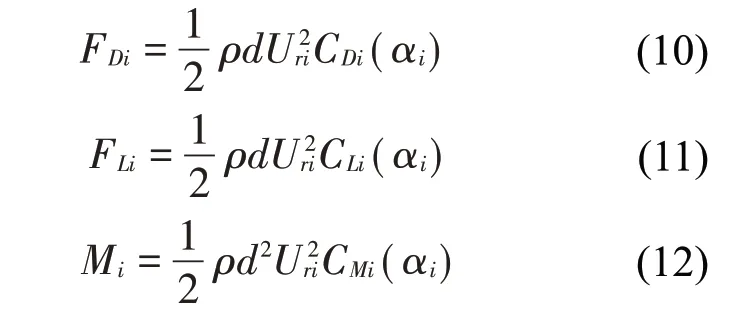
式中:ρ是空气密度,d是覆冰裸导线直径,CLi、CDi和CMi分别是覆冰子导线的升力系数、阻力系数和扭矩系数,可以通过风洞试验获得。在稳定风作用下,处于风场上游的子导线会吸收风中的能量,在风场的下流区形成尾流区域;处于下游风场的子导线输入风速会低于处于上游风场的子导线输入风速,同时下流风场区域的湍流强度会增强;由于空气尾流效应,使得分裂导线所处的风场风速分布不均,从而造成各子导线的空气动力系数不同。本文在研究导线舞动稳定性时考虑了尾流效应的影响。在计算覆冰导线的动态响应时,需要将子导线的升力和阻力投影到z轴和y轴,可得:
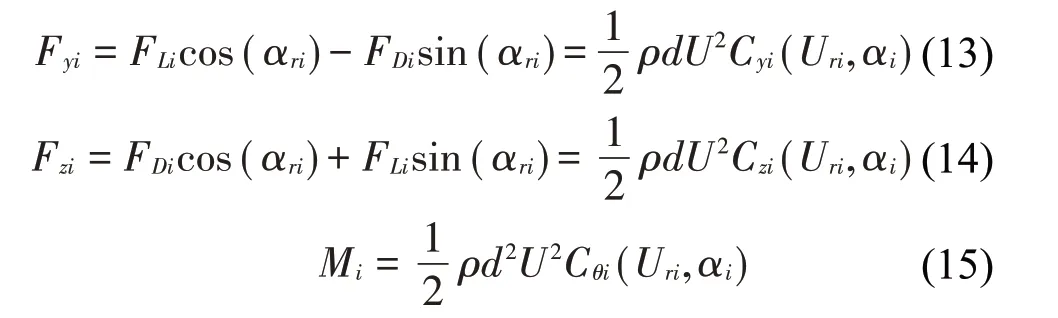
这里:Cyi、Czi和Cθi分别是子导线竖直、水平和扭转方向的空气动力系数,可以表示为
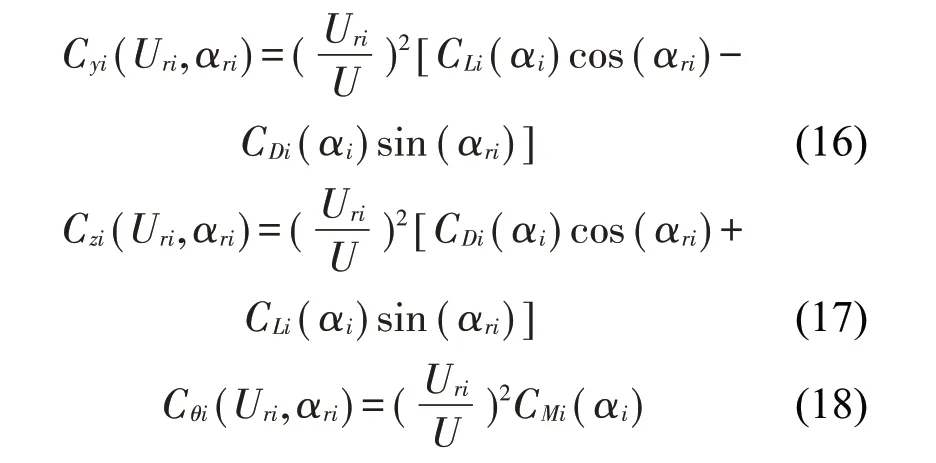
由于空气尾流效应的影响,四分裂导线整体风荷载由各子导线风荷载叠加等效得到。将4根子导线的升力、阻力和扭矩平移到四分裂导线的中心,根据平移定理可得:

这里:Cy、Cz分和Cθ别是四分裂导线竖直、水平和扭转方向的整体空气动力系数,可以表示为
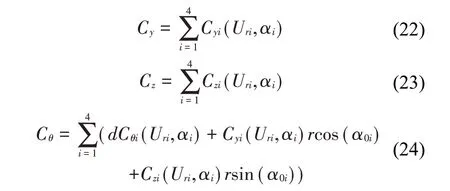
竖直、水平和扭转方向的整体空气动力系数可以在初始风攻角α0处进行泰勒展开,其线性部分可以表示为

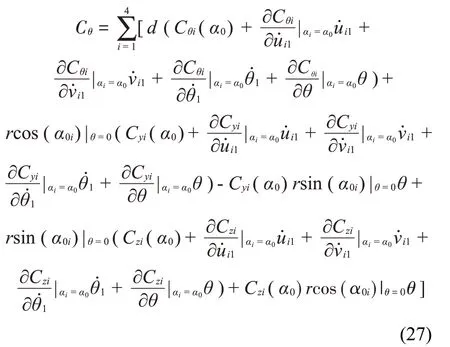

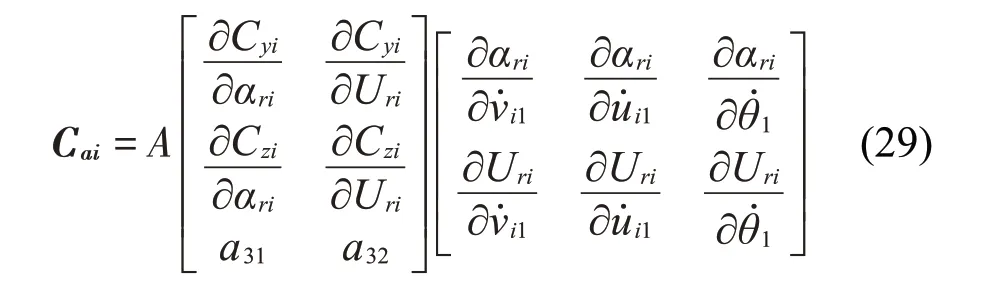

A=Kai为子导线载荷刚度矩阵,可以表示为
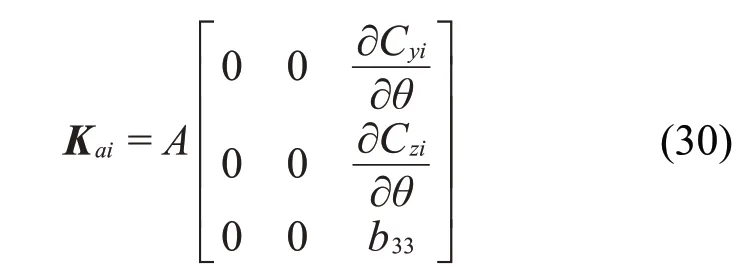

其中:

整理后可得空气动力阻尼矩阵为
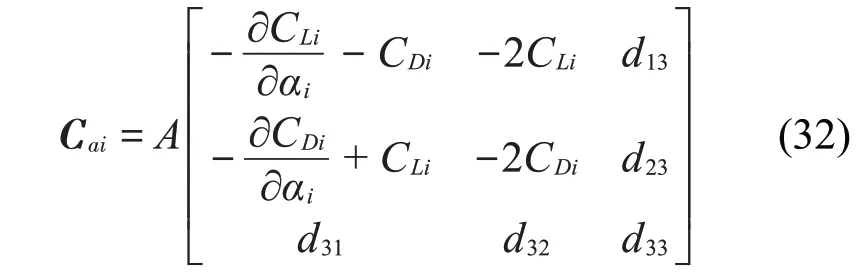
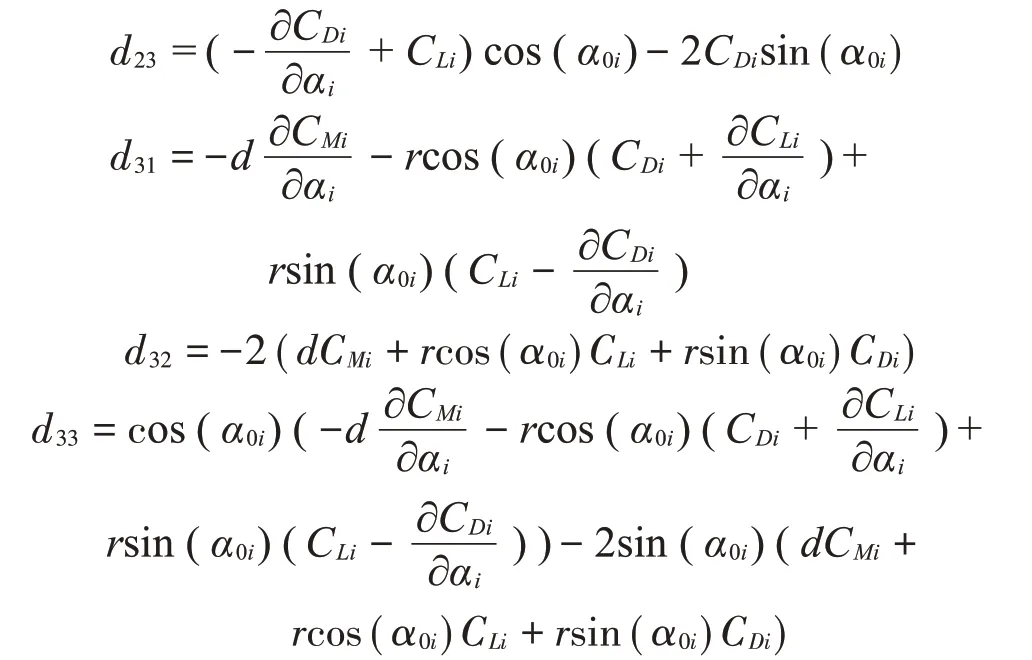
化简后可得载荷刚度矩阵为

其中:
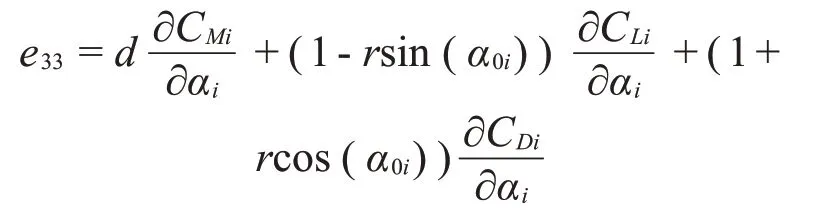
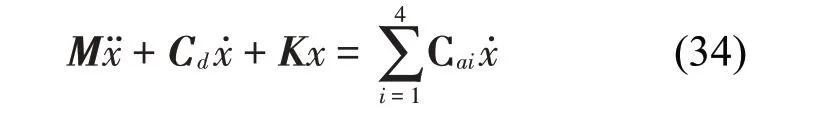
其中每一项表示的含义为

上式中覆冰四分裂导线单位长度的质量为m,转动惯量为J,3个自由度方向的阻尼比为ζy、ζz和ζθ,3个自由度方向的圆频率为ωy、ωz和ωθ。根据式(34)可以得到系统的阻尼矩阵为
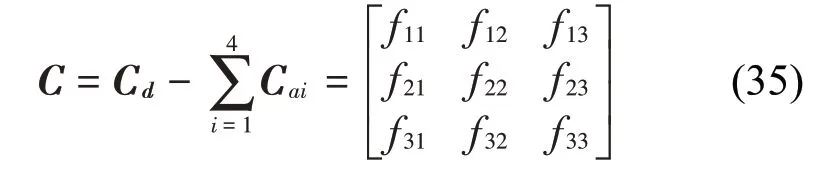
其中:

当仅考虑竖向运动时,系统阻尼矩阵中对角元素第一项f11即为Den Hartog判断舞动的准则。当考虑扭转诱发舞动时,系统阻尼矩阵中对角元素第三项f33即为Nigol 判断舞动的准则。本文中基于3 自由度运动进行稳定性分析,为了分析该系统的稳定性,令X=Xeλ t,则特征多项式可以根据式(34)得到:
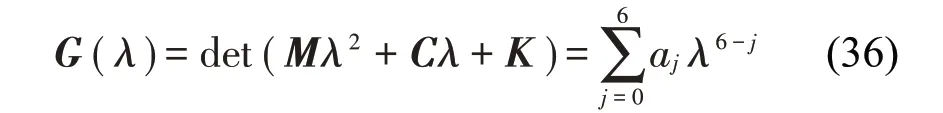
其中多项式的各个系数如下

如果系统矩阵式(35)为正定矩阵,则这个动力系统稳定。根据Rourh-Hurwitz准则,这个动力系统稳定的条件是:

上式中各个参数可以表示为
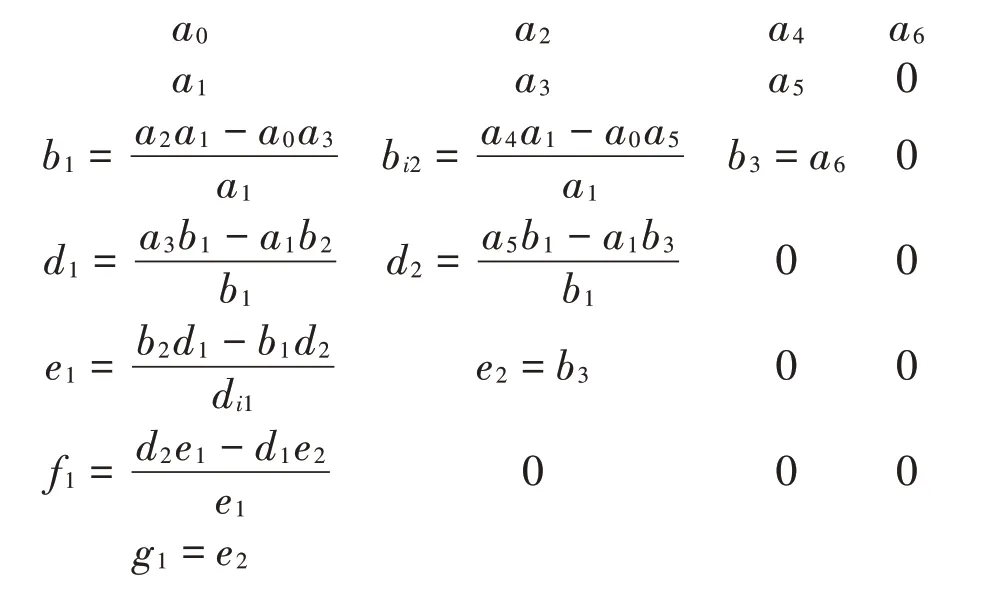
2 风洞试验与气动特性分析
前一节完成了覆冰导线临界风速计算公式的推导,计算临界风速需要导线的空气动力系数。为了获取新月形覆冰四分裂输电线的空气动力系数,在中国空气动力研究与发展中心低速所的1.4m×1.4m低速风洞中进行了模型测试,这个风洞外形如图3(a)所示。测试模型如图3(b)所示,四分裂导线模型由顶底板连接在一起置于风洞中,裸导线内部安装了测力天平,裸导线外部粘贴了新月形木材来模拟覆冰。当风流经过该覆冰导线时,测力天平可以测量出新月形覆冰四分裂导线所受到的升力FL、阻力FD和扭矩M。初始风攻角为0°;每测量一次气动载荷后,覆冰导线模型逆时针转动5°,然后再测量一次气动载荷,转动范围为0°~180°,四分裂导线的布置和风攻角的变化如图3(c)所示。
本实验设置3种覆冰厚度进行试验,覆冰厚度分别为12 mm,20 mm,28 mm;本文选取覆冰厚度为20 mm时的情况来分析空气尾流效应对各子导线气动系数的影响,试验风速为14 m/s。通过风洞试验测得新月形覆冰四分裂导线空气动力系数随风攻角变化曲线如图4所示。
各子导线的空气动气系数大致是相同的,但是由于尾流效应的影响,各子导线的空气动力系数在局部会有不同。导线阻力系数随风攻角变化的曲线大致呈半波状,当风攻角α=0°时,此时导线的迎风面积最小,阻力系数也最小;子导线3处于子导线1的尾流区,其阻力系数小于子导线1。当风攻角α=45°时,子导线3、4处于子导线1、2的尾流区,其阻力系数降低。当风攻角α=90°时,导线的迎风面最大,阻力系数出现了峰值,子导线4处于子导线2的尾流区,其阻力系数明显降低。同样地,当风攻角α=135°和α=180°时,对应尾流区子导线的阻力系数均有所下降。

图3 采用风洞测试空气动力系数
导线升力系数随风攻角变化的曲线大致呈正弦函数波状,子导线2 在模型转动过程中始终处于风场的上游,几乎不受尾流效应的影响,其空气动力系数变化曲线比较平缓,没有突变;当风攻角α=0°、α=90°和α=180°时,各子导线升力系数几乎都为0。
导线扭矩系数随风攻角变化的曲线大致呈正弦函数波状,当风攻角α=0°、α=150°和α=180°时,各子导线扭矩系数几乎都为0,且α=150°时,扭矩系数和升力系数相同。
3 临界风速计算
采用MTALAB编写判断和循环语句程序,将第2 节风洞试验所得的气动系数和文献[13]的导线频率代入式(19)和式(21),计算各种工况下不同舞动判断准则的临界风速。关于覆冰四分裂导线的扭转频率还没有得到大家公认的研究结果,为了使结果具有合理代表性,本文选取3个扭转频率值分别进行计算,即0.2 Hz、0.4 Hz 和0.6 Hz。现对计算的结果进行分析。
根据计算结果,选取覆冰厚度为20 mm、扭转频率为0.4 Hz、风攻角为165°时3种不同舞动理论的临界风速来对比验证本论文所提出的3自由度舞动判别准则。所得结果如图5所示。正方形曲线代表基于Den.Hartog理论所确定临界风速,圆形曲线代表基于Nigol理论所确定临界风速,三角形曲线代表基于本文3-DOF理论所确定临界风速。从图中可以看出基于Den.Hartog理论的临界风速随频率比值变化不大,其值在6 m/s~7 m/s之间。基于Nigol理论的临界风速不随频率比值变化,其值为8.2 m/s,Nigol理论只与扭转频率有关,所以其临界风速不会随面内和面外频率比值变化,是一个定值。
基于本文3-DOF理论的临界风速随频率比值的增大而减小,其值在7.5 m/s~14.7 m/s之间,由于本文3-DOF理论与3个方向的频率有关,考虑了3-DOF 之间能量的传递,其临界风速随频率比值变化明显。当频率比小于2时,根据本文3-DOF理论所确定临界风速大于根据Den.Hartog理论和Nigol理论确定临界风速;当频率比大于2时,根据本文3-DOF理论所确定临界风速与根据Den.Hartog理论和Nigol理论所确定临界风速接近。
根据计算结果,选取覆冰厚度为20 mm,风攻角为105°,在不同扭转频率下,采用本文3-DOF理论确定临界风速,所得结果如图6所示。
从图6中可以得出,扭转频率对临界风速影响较大;扭转频率为0.2 Hz和扭转频率为0.4 Hz时,临界风速最大相差3.5 m/s。根据3条曲线进行分析,随着扭转频率的减小,其临界风速减小;扭转频率减小其扭转刚度也会减小,导线驰振越容易发生。扭转频率为0.4 Hz和0.6 Hz时对应的临界风速随着频率比的增大而减小。扭转频率为0.2 Hz时对应的临界风速随着频率比的增大先增大后减小。
根据计算结果可知,选取扭转频率为0.4 Hz、风攻角为90°,在不同的覆冰厚度下,采用本文3-DOF理论确定临界风速,所得结果如图7所示。
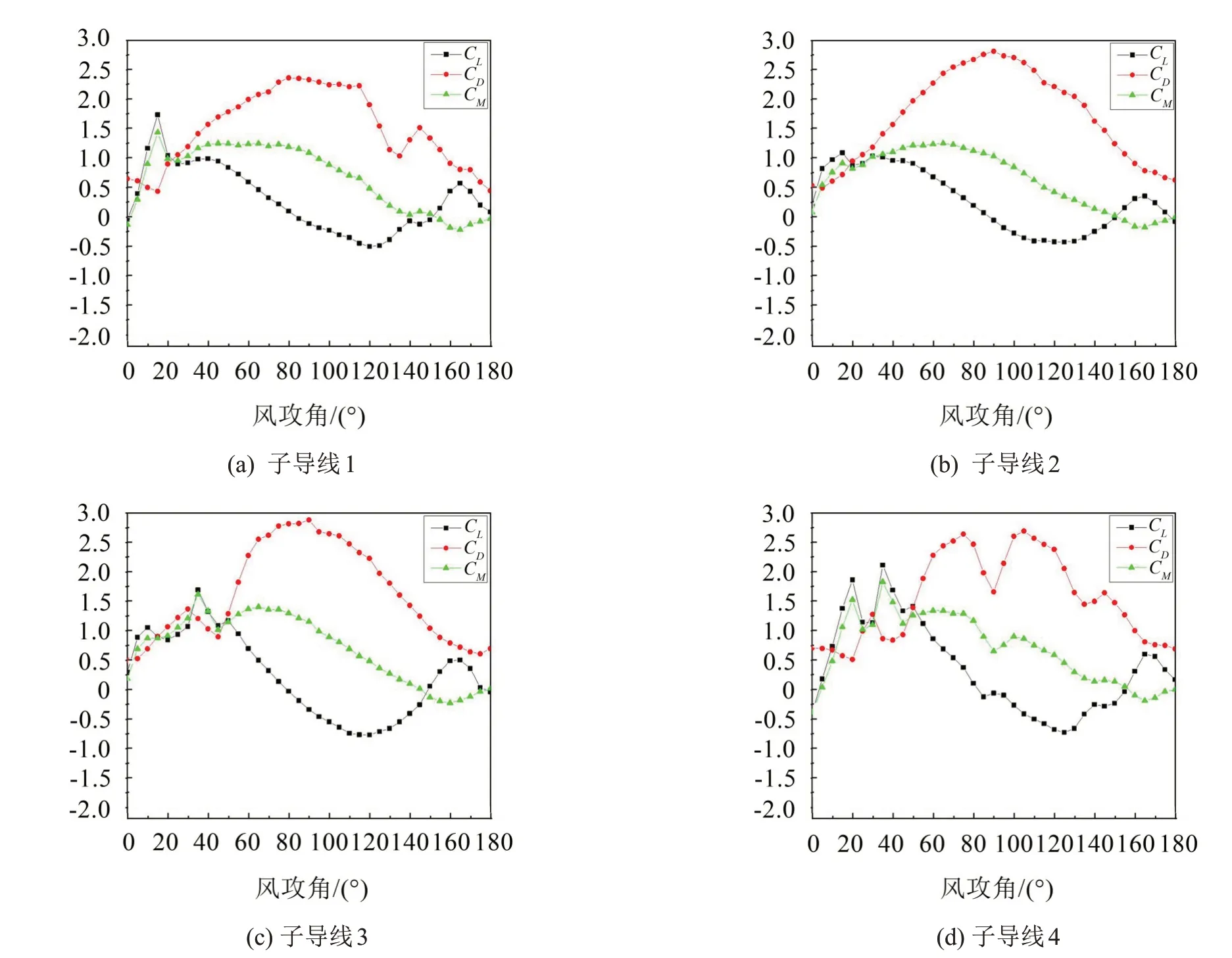
图4 覆冰四分裂导线空气动力系数
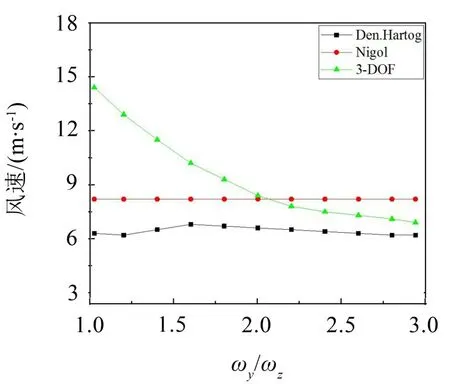
图5 基于不同理论的临界风速对比
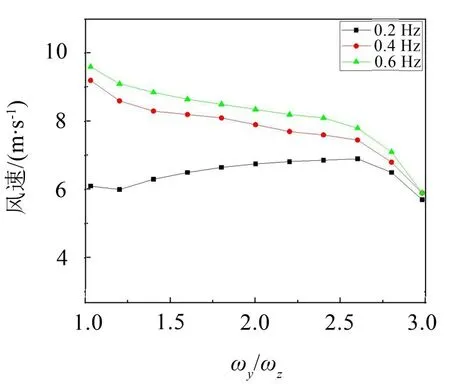
图6 不同扭转频率下的临界风速对比
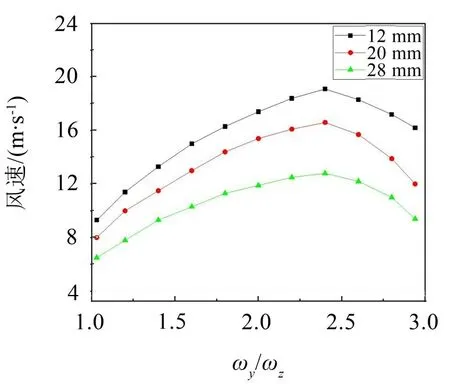
图7 不同覆冰厚度临界风速
从图7中可以看出,覆冰厚度对四分裂导线的临界风速影响较大。当覆冰厚度为12 mm和20 mm时,最大的临界风速差达到了7 m/s。随着覆冰厚度的增大,其临界风速减小;由于覆冰厚度的增加,导线迎风面增大,3个方向上的空气动力系数均有所增大,使得导线更容易发生舞动。面内外频率比接近1和3时,线路最易发生舞动。
4 结语
本文通过基本建立3自由度新月形覆冰四分裂导线的力学模型,将空气动力系数在初始风攻角处进行泰勒展开,得到气动荷载修正表达式。研究了覆冰四分裂导线在静力风作用下的舞动,忽略惯性耦合项以及载荷刚度项,得到3 自由度覆冰导线的振动方程。根据Rourh-Hurwitz稳定准则,推导了动力系统平衡稳定条件。在风洞试验中设置不同的覆冰厚度,通过风洞试验测得新月形覆冰四分裂导线在3个方向上的气动系数。运用本文的3 自由度稳定判别式计算出了不同的扭转频率和覆冰厚度所对应的临界风速。考察了不同情况下临界风速随面内外频率比变化特征。得到了以下结论:
(1)本文中所建的新月形覆冰四分裂导线的力学模型考虑了同一时刻子导线之间风攻角的差异,更加真实地反映了每一根子导线对应的位移和风荷载。采用本文方法得到的3自由度舞动判断准则更加详细地考虑了竖向运动、横向运动以及扭转运动对临界风速的影响,更加符合实际工程情况。计算结果显示,基于Den Hartog理论,可能发生舞动的风攻角为15°、165°、170°;基于Nigol理论可能发生舞动的风攻角为10°、165°、170°;基于本文3-DOF稳定理论可能发生舞动的风攻角为10°、55°、60°、70°、80°、95°、165°、170°;采用文中提出的理论确定的可能发生舞动的初始攻角范围比Den Hartog理论和Nigol理论确定可能发生舞动的初始攻角的范围更广。因此,采用本文所提出的3-DOF 稳定理论对线路防舞进行指导更合理。
(2)扭转频率对覆冰输电线舞动的临界风速有显著影响,随着扭转频率的减小,其临界风速减小;扭转频率减小意味着其扭转刚度也会减小,导线越容易发生舞动。因此在线路设计中应该选取能导致较高扭转频率的线路参数来进行防舞设计。
(3)覆冰厚度对输电线舞动的临界风速有显著影响,随着覆冰厚度的增大,其临界风速减小。在线路防舞设计时要特别注意覆冰厚度的影响。

