变截面功能梯度旋转轴的自由振动特性

李 震，关先磊，王青山，秦 斌

（1.中南大学 高性能复杂制造国家重点实验室，长沙410083；2.中南大学 交通运输工程学院 轨道交通安全教育重点实验室，长沙410075）

旋转轴作为动力传输的重要部件，在数控加工和航空航天等工程领域有着广泛应用。随着生产力发展，各向同性材料已经不能满足旋转轴高速旋转的工作要求，迫切需要具有特殊力学性能的新型材料来取代各向同性材料。功能梯度材料(FGM)作为一种新型材料具有改善质量分布、减少热应力、提高强度等一系列优点，引起国内外学者的关注。

葛仁余等[1]基于欧拉梁理论，采用插值矩阵法（IMM）研究了轴向力作用的轴向功能梯度欧拉梁的自由振动特性；汪亚运等[2]采用切比雪夫多项式得到轴向非均匀变截面梁的自由振动特性，并分析了梯度参数、边界条件等对固有频率的影响；韩伟等[3]基于欧拉-伯努利梁理论和动态刚度分析方法推导动态刚度矩阵，研究旋转变截面梁的自由振动特性；王囡囡等[4]基于哈密尔顿原理，建立中心刚体-柔性梁的动力学模型，研究旋转变截面梁的自由振动特性；关先磊[5]采用微分求积法来求解梁板壳耦合振动特性；张永旺等[6]基于Raleigh 梁理论建立柔性自转轴的动力学方程，运用Galerkin 方法求解系统的频率和模态；黄小林等[7]基于复合材料薄板理论推导出轴向运动功能梯度材料薄板的运动方程，采用Galerkin方法计算其自由振动和屈曲特性；陶彦鸣等[8]采用Chebyshev 谱方法研究变截面欧拉梁的动态特性。Dong等[9]通过假设模态法和拉格朗日方程推导旋转功能梯度锥形空心圆截面梁的动力学方程，求解梁的自然频率与模态；Shabanlou等[10]运用高阶剪切变形梁理论进行功能梯度旋转圆柱梁的自由振动特性研究；Huang 等[11]采用Spectral-Tchebychev方法推导旋转功能梯度锥形圆截面梁的控制方程，研究其旋转频率和临界转速；Nikbakht 等[12]详细介绍了功能梯度结构的性能，并对其进行系统的概述。

本文基于铁木辛柯梁理论得到变截面功能梯度旋转轴的动能和势能，将能量表达式用微分求积权系数矩阵表示，得到单元质量矩阵和刚度矩阵,利用有限元法对上述所求的单元矩阵进行组装得到整体质量矩阵和刚度矩阵以及陀螺矩阵。将基于微分求积有限元(DQFEM)得到的变截面功能梯度轴的无量纲频率与参考文献对比，验证本方法的准确性、稳定性和通用性；紧接着在简支边界条件下探究变截面锥度系数和梯度系数对变截面功能梯度旋转轴固有频率的影响；最后在简支边界条件下探究变截面锥度系数和梯度系数对变截面功能梯度旋转轴临界转速的影响。

1 理论推导

1.1 模型描述

图1所示为变截面功能梯度旋转轴的动力学模型。该模型基于铁木辛柯梁理论，考虑4个自由度，用us和vs分别表示沿x轴和y轴方向移动；θx和θy分别表示绕x轴和y轴方向旋转。其材料属性沿z轴方向连续变化，即材料密度ρ、弹性模量E、剪切模量G是关于z的变量。

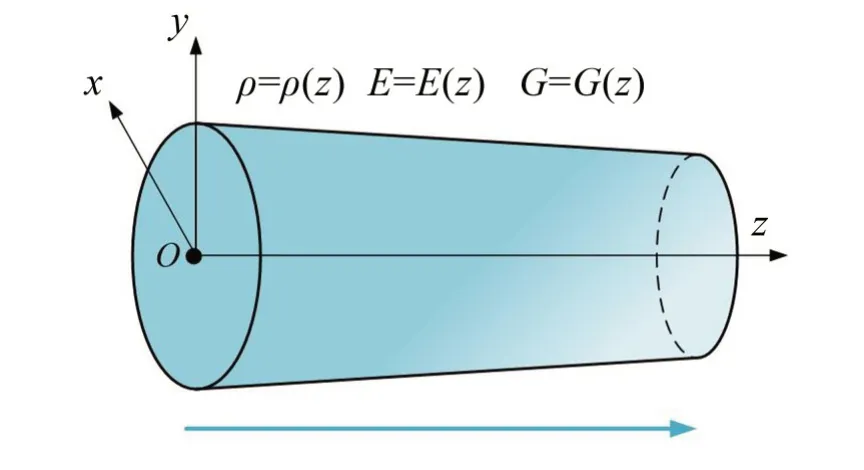
图1 变截面功能梯度旋转轴

1.2 动 能

如图2所示，在静止坐标系下，以转轴中心线上的一点为研究对象，其中rO0OP表示转轴上一点的位移矢量，i0、j0、k0、i1、j1、k1分别表示静止坐标系和连体坐标系下的方向向量，通过式(1)在静止坐标系和连体坐标系下分别求解位移矢量rO0O1和rO1P,并进行矢量叠加得到在静止坐标系下转轴上任意一点的位置矢量r0op。

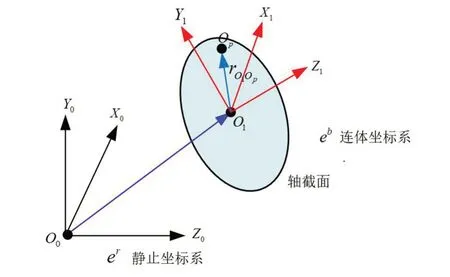
图2 矢量示意图

对于转轴上一点转动的描述，可将旋转轴类似刚体进行处理，即将转轴上一点转动转化为刚体定点转动。本文采用卡尔丹角描述刚体定点转动，结果如图3所示：

(1)坐标系xyz绕x轴转动α得到坐标系x1y1z1；

(2)坐标系x1y1z1绕y1轴转动β得到坐标系x2y2z2；

(3) 坐标系x2y2z2绕z2轴转动γ得到坐标系x3y3z3(ξηζ)；

通过上述3次转动实现坐标系xyz到坐标系ξηζ之间的转换，式（2）是实现xyz到ξηζ的坐标变换矩阵。

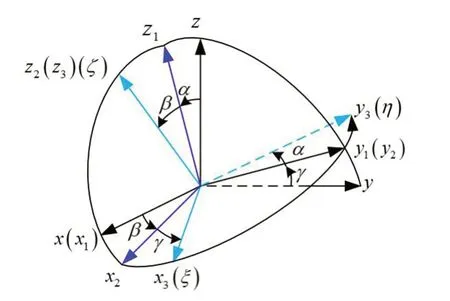
图3 卡尔丹角

采用卡尔丹角描述刚体的定点运动，角速度的合成也是采用矢量叠加，在连体坐标系下任意一点角速度分别用ωb表示。

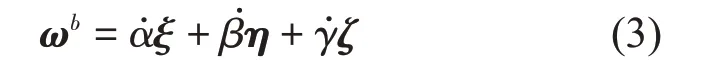
由于α、β、γ值较小，参考《多刚体动力学基础》[13]对变换矩阵进行简化，得到矩阵A1。

通过简化后坐标变换矩阵，可以求得在连体坐标系下转轴上任意一点相对于静止坐标系的角速度ωrb。

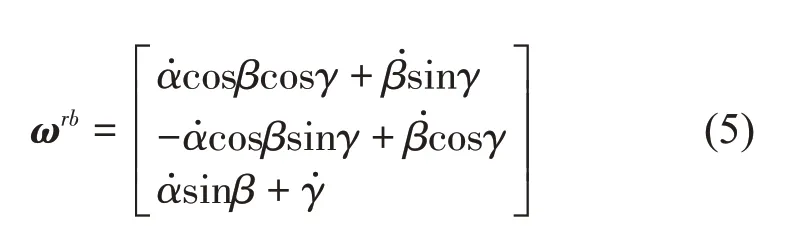
对于刚体上一点转速的计算，参考《理论力学》[14]中刚体运动学中运动坐标与牵连速度的描述，计算转轴上一点转速。

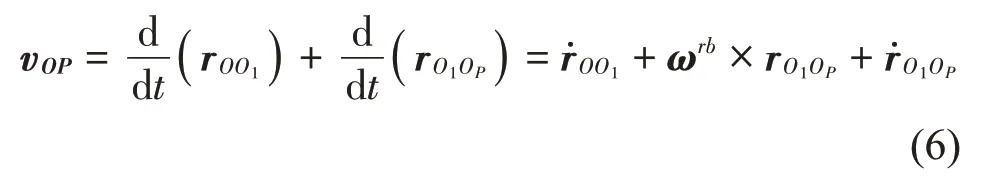
将根据式(6)求得转速代入到式(7)计算转轴动能。

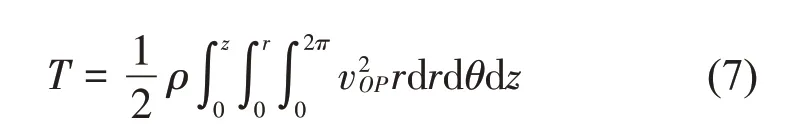
从而通过计算可以得到静坐标系下转轴动能的表达式(8)，其中S表示轴的截面积，I表示截面惯性矩。

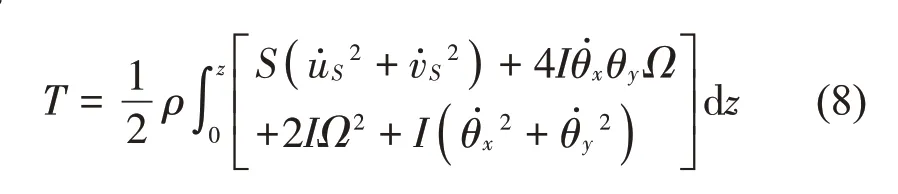
1.3 势能

基于铁木辛柯梁理论，考虑剪切变形和弯曲变形，转轴势能表达式见式(9)，具体推导过程参考文献[15]，其中E表示弹性模量；I表示截面惯性矩；κ表示剪切因子；G表示剪切模量；S表示截面积；其转轴势能表达式可以表示为

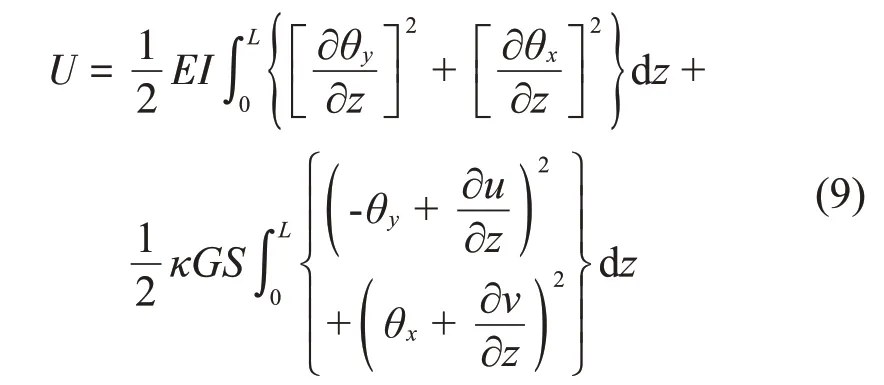
1.4 微分求积的原理

微分求积是基于数值分析方法将描述边值问题的微分方程转化成一组代数方程的形式，实现快速求解。设自变量x的一维函数为f(x)，在区间[-1，1]上连续可导。在区间[-1，1]上取N个不同节点，则函数在xi的1阶导数可以表示为

式中：A(ij1)，i，j=1，2，…，N，是1阶权系数，上角标“(1)”表示函数取1阶导数。由权系数A(ij1)组成的矩阵A(1)为1阶权系数矩阵，f为单元位移列向量。

微分权系数矩阵A(1)需要选取相应的插值基函数来获得，采用拉格朗日作为插值基函数，因其具有较好的递推关系。

类似于微分处理的节点划分，用数值积分方法在[-1，1]的积分区间对函数进行积分，则有：

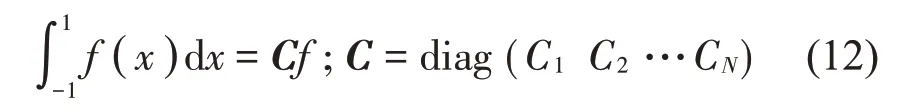
积分权系数矩阵C中的元素可用常规的数值积分方法求解，f是单元位移列向量。本文采用高斯洛巴托求积方法求解，其中权系数为

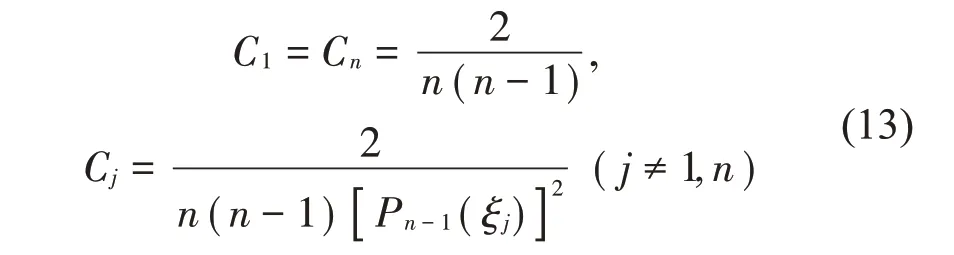
Pn(ξj)是n阶勒让德多项式，ξj(j=1，2，…，n-1，)是Pn-1(ξj)1阶导的第(j-1)个零点，Cj表示积分权系数矩阵中的项。为了使权系数矩阵适用于不同长度轴单元的求解，需要对权系数矩阵进行修正：

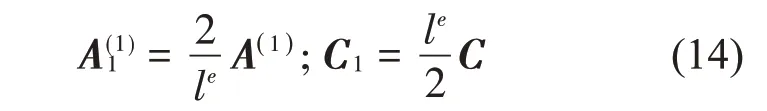
其中le表示转轴单元的长度。

1.5 微分求积的引入

将能量表达式当中的项用微分和积分权系数矩阵以及单元位移列向量进行表示。

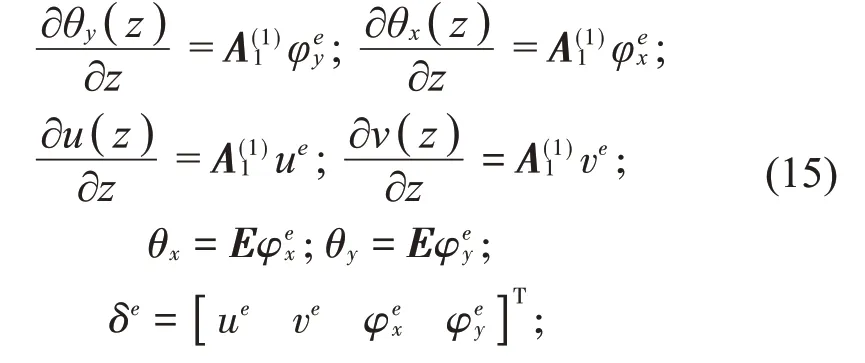
式中：δe表示单元位移列向量；ue、ve、φex和φey分别表示各个自由度上的单元位移列向量。本文讨论变截面功能梯度旋转轴，其弹性模量E、剪切模量G、密度ρ、截面面积S、惯性矩I沿轴向变化，都是N维对角矩阵。例如：E=diag(E（z1），E（z2），…，E(zN))，其中diag表示对角矩阵。

将上述所有参数代入势能表达式，得到下列微分求积形式的表达式，求解单元刚度矩阵：

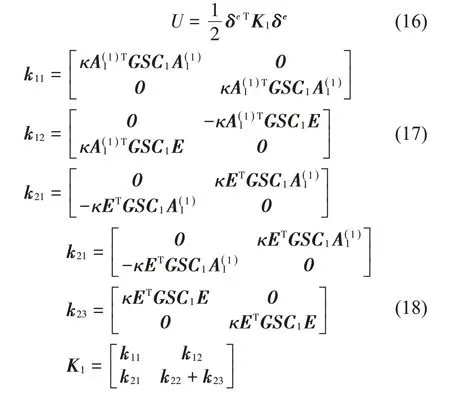
式中：K1表示关于转轴单元的刚度矩阵。

式中：M1和M2是关于转轴单元的质量矩阵。

由此得到了转轴动能和势能矩阵形式的表达式，为了求解转轴单元的质量矩阵、陀螺矩阵和刚度矩阵，本文将上述动能和势能的矩阵形式代入到拉格朗日方程求解系统总体的矩阵方程：

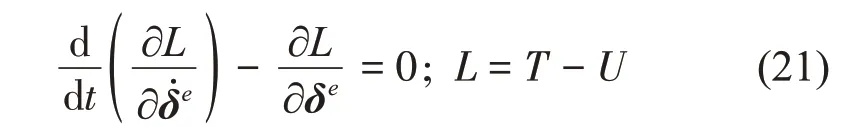
根据式（21）可以得到转轴单元的矩阵方程，进一步确定转轴单元的质量矩阵Me、刚度矩阵Ke以及陀螺矩阵Ge的组装矩阵，具体的表达式如下：

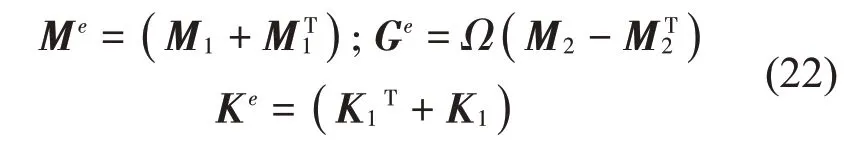
根据式（22）可以确定转轴单元的质量矩阵Me、陀螺矩阵Ge和刚度矩阵Ke。为了得到转轴系统整体的质量矩阵M，陀螺矩阵G和刚度矩阵K，本文采用“对号叠加法”将转轴的单元矩阵集成到总体矩阵中。对号叠加法的关键是根据节点号和自由度号得到单元矩阵在整体矩阵当中行号和列号，由于每个节点的自由度是4，所以节点号为n的第p个自由度在整体矩阵中的行号（或列号）为Q=（n-1）*4+p。本文采用微分求积的积分节点取值为n1=19，且n=n1+1。紧接着对已获得的M、G和K采用组装矩阵方式进行处理，其组装矩阵表达式如式(23)所示：

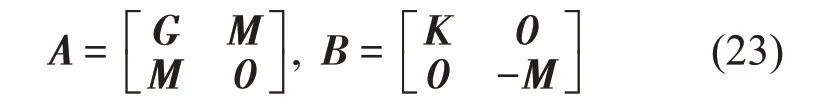
紧接着借用MATLAB平台采用eig函数求解相应的模态频率和模态向量。相应的表达式如下：

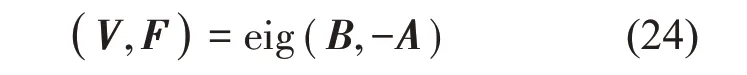
式中：V和F分别表示模态向量和模态频率。

1.6 变截面理论

变截面轴分为两种，分别是面积线性变化和半径线性变化。本文讨论半径沿轴向线性变化的变截面旋转轴，变截面主要引起截面面积以及截面惯性矩的变化。设左侧截面半径为r0，右侧截面半径为r1，变截面轴的长度为L，变截面锥度系数为c（一般取值为0～0.8），z表示距离左侧的轴向距离。

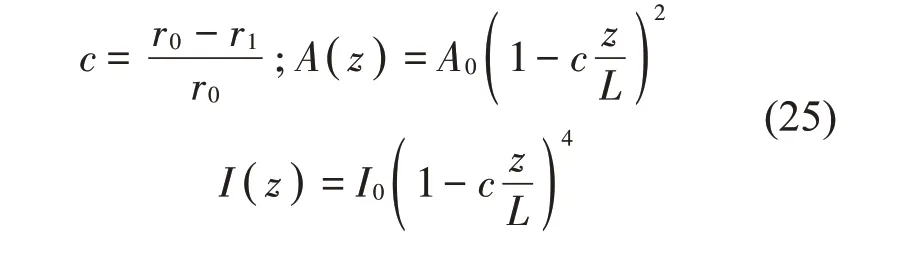
1.7 功能梯度理论

功能梯度材料是一种非各向同性材料，弹性模量和密度沿轴向呈幂等规律变化，其变化规律取决于梯度系数m（一般取0至10）。Es表示左侧截面弹性模量，ρe表示左侧截面密度，Es表示右侧截面弹性模量，ρe表示右侧截面密度，其余参数同上。

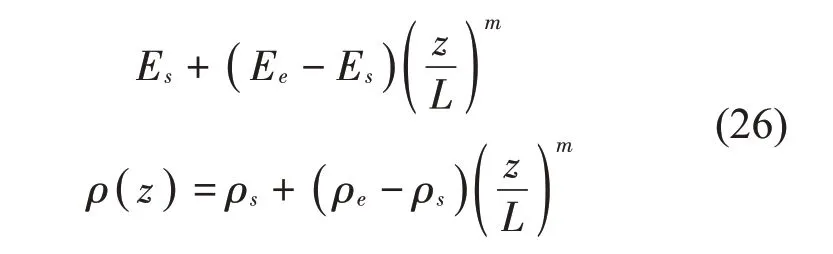
2 算例分析

为了便于编程求解变截面功能梯度旋转轴的自由振动特性，本文给出了相应的算法流程图，如图4所示。

2.1 算法验证

为了验证本方法的收敛性和准确性，采用文献中的经典案例进行验证，为了便于与文献进行对比令转速v=0，同时假定功能梯度材料是由ZrO2和Al构成，其材料属性沿着轴向呈幂等规律变化，具体的变化规律如式(24)所示。ZrO2材料的弹性模量和密度分别是Es=200 GPa和ρs=5 700 kg/m3；Al材料的弹性模量和密度分别是Ee=70 GPa 和ρe=2 702 kg/m3；变截面轴的长度L=1 m；轴的大径r1=0.1 m；轴的细长比r=0.01；剪切因子为5/6；泊松比v=0.3；功能梯度系数m=2。本文均采用上述参数进行研究，为了便于与文献进行对比，需要将求得的频率无量纲化，引入固有频率无量纲化的公式，关于细长比（回转半径）定义如下：

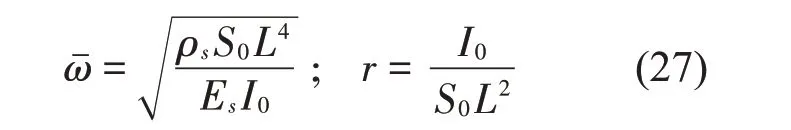
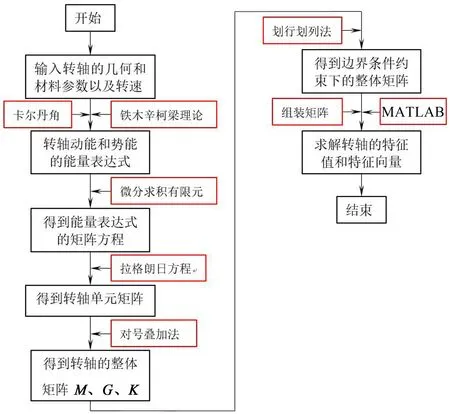
图4 算法流程图

计算结果如表1所示。

从表1看出。DQFEM算法和有限元算法[16]的计算结果基本吻合。可以验证该算法的收敛性和正确性。

关于变截面功能梯度旋转轴转速的研究目前没有能找到相关的文献进行对比研究，本文在简支边界条件下，取变截面功能梯度旋转轴的极端情况(m=0；m=∞)与ANSYS的仿真结果进行对比验证(ANSYS 中选用BEAM188 单元，划分100个单元)，变截面功能梯度旋转轴的转速为500 rad/s。

从表2中看出,采用DQFEM算法与ANSYS算法在两种极端情况下得到的固有频率误差在1%以内，验证施加转速时的正确性。在此基础上进行变截面功能梯度旋转轴转速的研究。

表1 不同边界条件不同锥度系数的无量纲频率

表1 不同边界条件不同锥度系数的无量纲频率

?

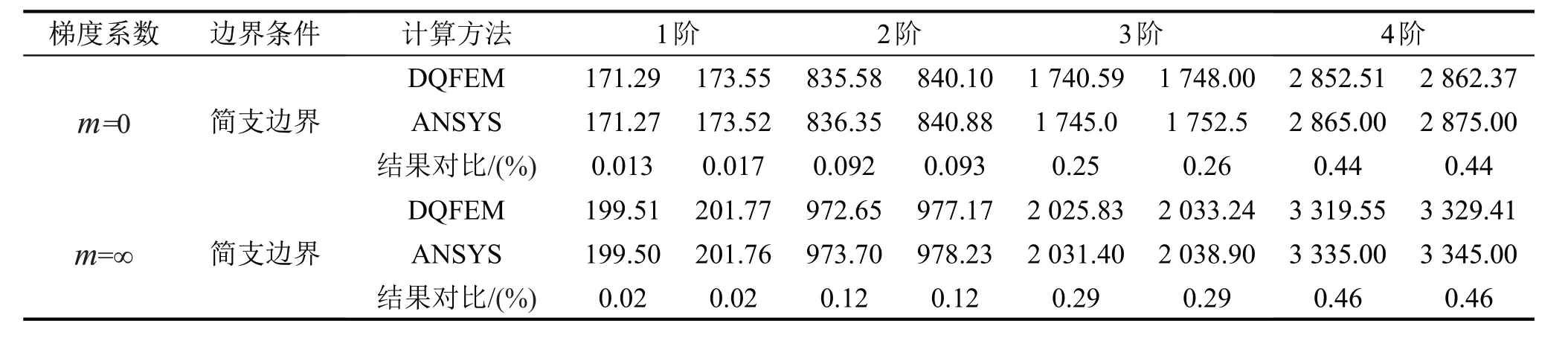
表2 变截面功能梯度旋转轴极端情况下固有频率对比

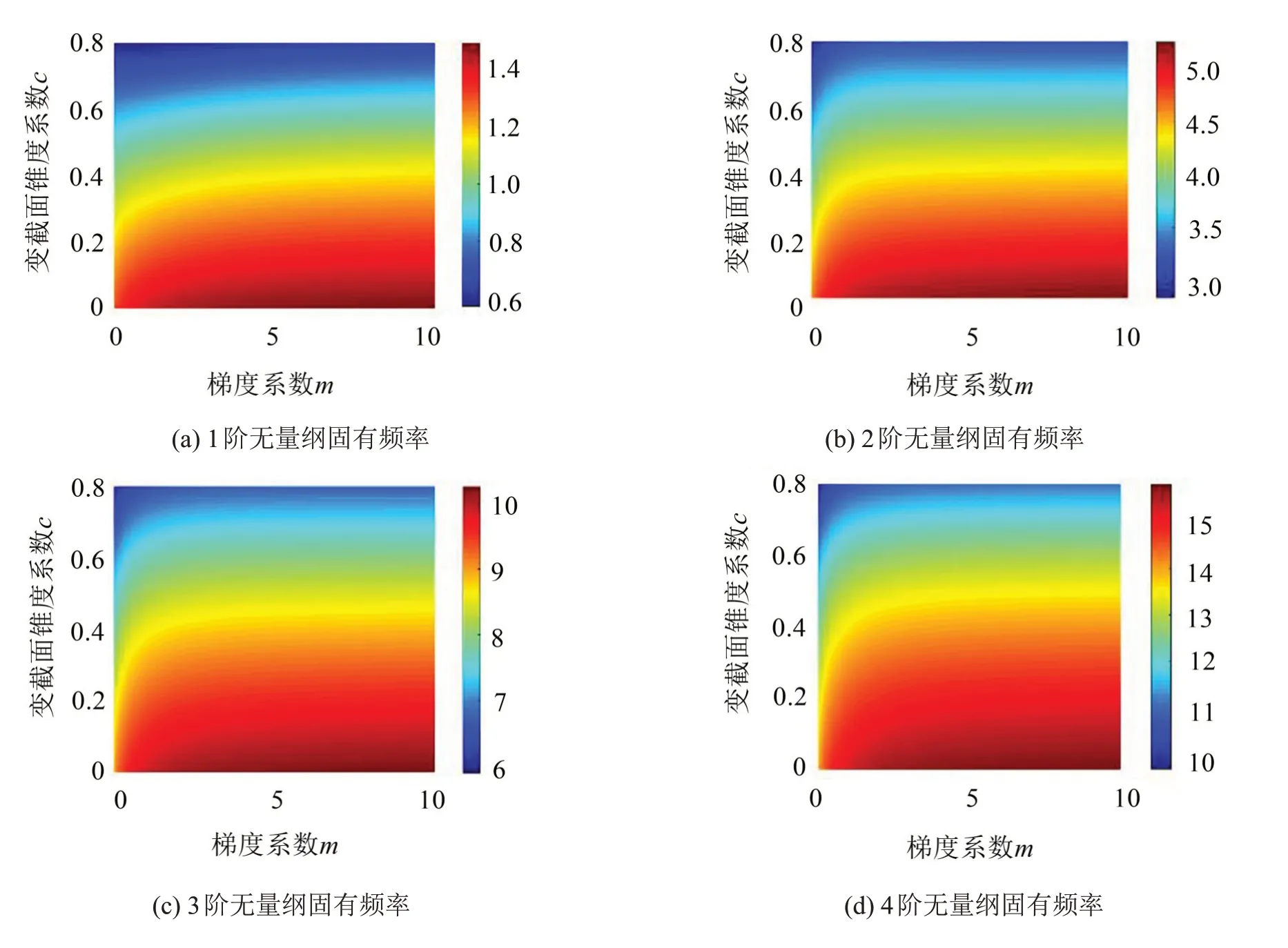
图5 无量纲固有频率变化

2.2 变截面锥度系数和梯度系数对固有频率的影响

上述对比验证本文方法的正确性，结合工程实际应用，本文仅在简支边界条件下探究变截面锥度系数以及梯度系数对功能梯度旋转轴固有频率的影响。同时指出此时的转速为0，其他具体参数如2.1节所示，相应的结果如图5所示。

如图5所示，在简支边界条件下，变截面功能梯度轴的无量纲固有频率随着变截面锥度系数的增加呈现出降低的趋势,随着梯度系数增加，呈现出先逐渐增加，后保持不变的变化趋势。从上述4阶无量纲固有频率的变化曲线中看出，当梯度系数大于2以后，梯度系数的增加对无量纲固有频率几乎不产生影响。

2.3 变截面锥度系数和梯度系数对临界转速的影响

由上所述，临界转速是工程应用中极为重要的参数，因此有必要研究变截面锥度系数和梯度系数对临界转速的影响。本文首先研究变截面功能梯度旋转轴在简支边界条件下以及特定变截面锥度系数和梯度系数条件下转轴前后涡动频率随转速的变化规律，其中梯度系数m=2，变截面锥度系数c=0.8，其他具体参数如2.1节所示，得到如图6所示的整体坎贝尔图。

图6 整体坎贝尔图

从图6中不难看出，变截面功能梯度旋转轴涡动频率（固有频率）随转速增加出现分岔现象，分为前涡动和后涡动，前涡动频率随转速的增大而增大，后涡动频率随转速的增大而减少。图6中斜线是描述涡动频率与转速相等的一条直线，该直线的表达式为ω=Ω。同时指出，该直线与前涡动频率的交点所对应横坐标值是临界转速。图中ΩI、ΩII、ΩIII和ΩIV分别表示1阶、2阶、3阶和4阶临界转速。为了能够直观描述上述现象，本文将图6中的坎贝尔图进行局部放大，结果如图7所示。

同时有必要给出变截面功能梯度旋转轴临界转速的表达式，以便开展关于临界转速的研究。首先求解前涡动频率直线的解析表达式，然后将表达式与解析式为ω=Ω的直线联立求解得到临界转速。假设转速为Ω=0时，前涡动频率为ω1；转速为Ω=1 000时，前涡动频率为ω2，则涡动曲线的表达式为

图7 局部放大坎贝尔图

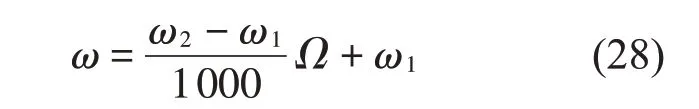
将式（28）与ω=Ω进行联立可得临界转速的表达为

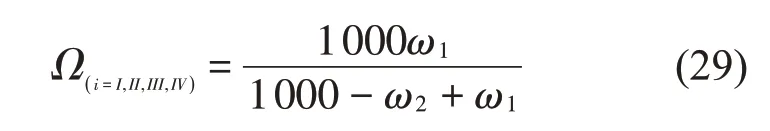
基于以上讨论，确定了临界转速的计算方法，紧接着研究变截面功能梯度旋转轴在简支边界条件下变截面锥度系数和梯度系数对临界转速的影响，具体参数见2.1节，相应的结果如图8所示。

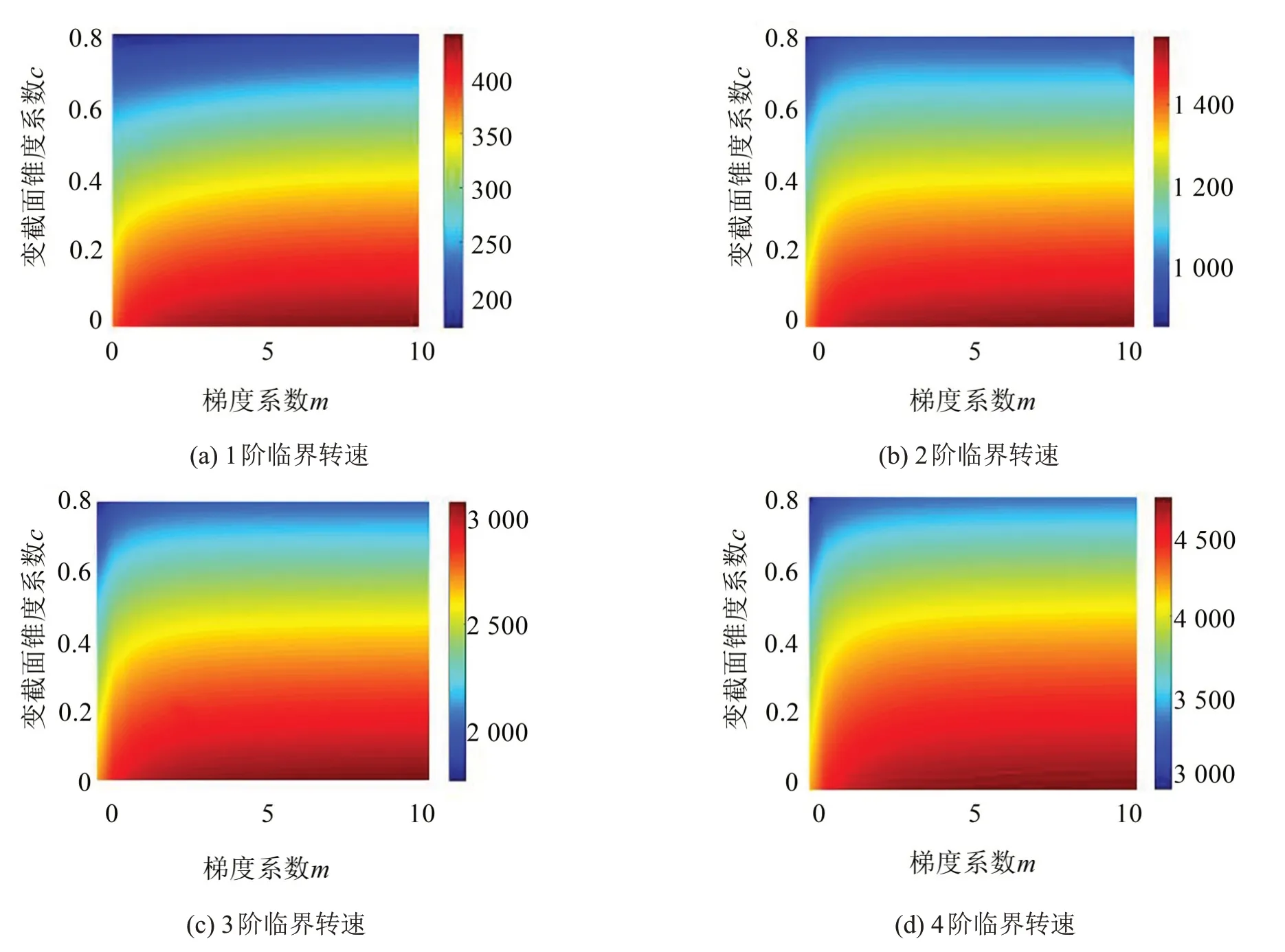
图8 简支边界条件下临界转速的变化

从图8可以看出，在简支边界条件下，研究变截面功能梯度旋转轴临界转速随变截面锥度系数以及梯度系数的变化，4阶临界转速的变化趋势相同，随着变截面锥度系数的增加，临界转速逐渐降低，随着梯度系数增加，临界转速先增加后保持不变。

3 结语

(1)本文计算结果分别与已有文献结果和有限元ANSYS 计算结果的对比验证证明本文方法具有准确性、稳定性和通用性，适用于求解变截面功能梯度旋转轴的自由振动问题。

(2)在模型验证的基础上，开展了关于变截面功能梯度旋转轴固有频率的研究，主要探究变截面锥度系数和梯度系数对固有频率的影响，结果表明上述参数对固有频率有重要影响。

(3)根据已建立的模型，进一步研究了变截面功能梯度旋转轴涡动频率随转速的变化规律，给出了临界转速的定义，并进一步探究变截面锥度系数和梯度系数对临界转速的影响，对实际工程应用具有重要的意义。