自适应半主动悬架系统机械硬件在环试验研究

朱玉刚，卞学良，陈达亮，石 岩，靳天石

(1.河北工业大学 机械工程学院，天津300401；2.中汽研（天津）汽车工程研究院有限公司，天津300300；3.西南交通大学 机械工程学院，成都610031）

随着电动化、智能化、网联化及共享化的快速发展，车辆各个系统电控集成度逐步提升。由于对驾乘舒适性、操纵稳定性及安全性均有较大影响的悬架系统是线控底盘系统的重要组成部分，电控悬架系统已成为学者及工程人员关注的焦点。

电控悬架系统根据刚度阻尼可调参数不同分为半主动悬架和主动悬架，而主动悬架系统由于系统耗能高、成本贵及控制策略复杂等因素目前只限于学术研究。而半主动悬架系统具有控制效果接近主动悬架系统且系统耗能低、成本少、鲁棒性强等优点，已被广泛应用于量产车型，如大众途锐、奔驰GL450及通用新君越等。目前用于半主动悬架系统研发的控制算法主要有：滑模控制[1-2]、反推控制[3-4]、模糊控制[5]、H∞控制[6]、自适应控制[7-8]、模型预测控制[9-10]、神经网络控制[11-12]等。在算法可实现性和工程应用等方面，以Karnopp 等最早提出的天棚控制策略(Skyhook control，SH)最为著名[13]。Sammier等提出了改进的线性天棚控制，能够根据车身振动速度线性调节阻尼范围[14]。Liu 等提出了新的天棚控制一般理论，仿真结果表明，采用一般天钩控制理论的半主动悬架具有较好的控制效果[15]。Savaresi 等提出了加速度阻尼控制(Acceleration driven damper，ADD)，并利用最优控制理论证明了其有效性[16]。在对比分析了开关型的SH 和ADD的优缺点后，Savaresi等提出了Mixed SH-ADD算法，可在全频域范围内降低车辆振动加速度[17]。郭孔辉等提出了一种改进的加速度阻尼控制方法，从相频的角度进行理论分析并用四分之一悬架台架进行了试验验证[18]。Liu 等提出了Mixed SH-PDD控制算法，利用能量流对算法进行分析，不仅可在激励频域内降低振动加速度，还可以减少振颤[19]。以上方法主要集中在对半主动悬架系统的垂向进行控制，并且受限于试验验证手段，主要是对基于四分之一悬架模型进行仿真和试验验证。

本文提出了一种基于车身姿态补偿控制与天棚加速度控制相结合的算法，建立了自适应阻尼控制系统，不仅使车辆垂向运动的振动效果得到改善，还能兼顾车身俯仰侧倾控制，使其控制效果更加接近主动悬架。另外，本文搭建了一种新型的减振器机械硬件在环试验台，可以对车辆垂向、俯仰及侧倾运动进行控制算法有效性的验证，克服了四分之一减振器台架仅能验证车辆垂向运动的局限性，可以在无实车条件下对控制算法的有效性进行验证，丰富了半主动悬架系统开发的试验手段，缩短了项目开发周期。

1 整车动力学模型

为了对车辆垂向、俯仰及侧倾耦合运动控制进行更好的研究，本文建立了7 自由度整车动力学模型[20]，如图1所示。将悬架系统进行线性化，假设车辆俯仰及侧倾较小，通过数学模型计算得出车辆状态变量方程。

整车模型的符号标志定义如表1所示。

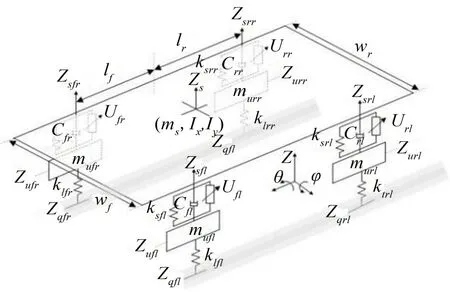
图1 整车动力学模型

表1 车辆符号标志定义

根据图1所示的车辆动力学模型，利用牛顿第二定律，簧载质量的轮跳运动方程如式(1)所示：

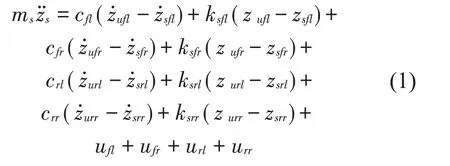
簧载质量的俯仰运动方程如式(2)所示：

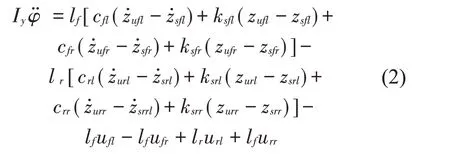
簧载质量的侧倾运动方程如式(3)所示：

左前轮的垂向运动方程是：

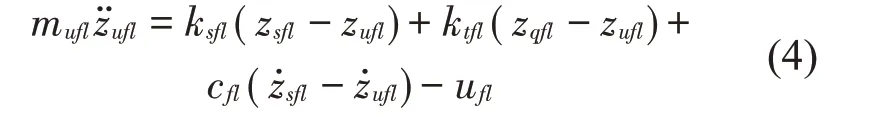
右前轮的垂向运动方程是：

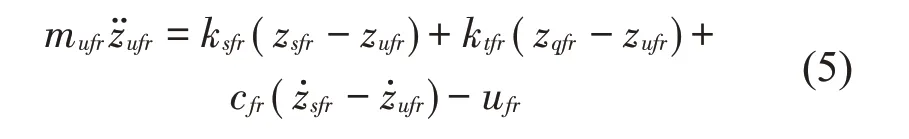
左后轮的垂向运动方程是：

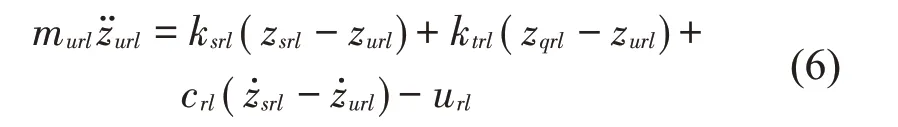
右后轮的垂向运动方程是：

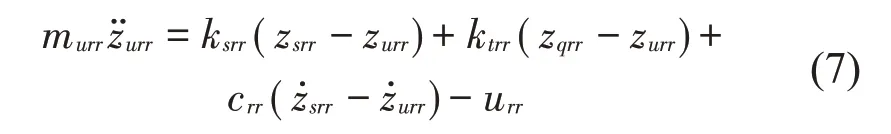
这里：

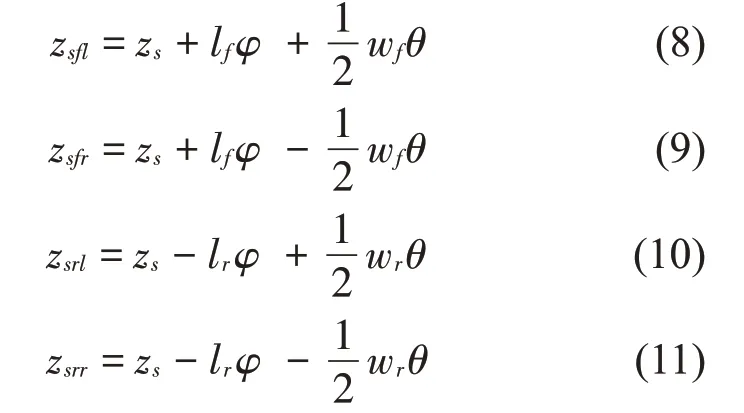
选择以下的状态变量、扰动量及控制量：

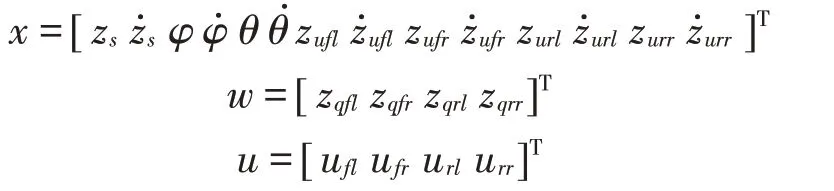
半主动悬架系统的状态方程如下：

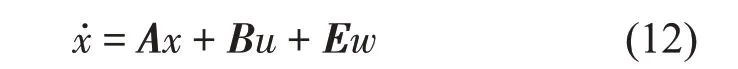
2 控制策略设计

2.1 分频天棚-加速度混合控制（SH-ADD）

上文所述的天棚阻尼控制[13]与加速度控制[16]中，前者与后者分别在相对低频和相对高频的范围内拥有更优的舒适性，因此，建立一个分频规则，可在不同频段下切换SH与ADD 控制策略，则可达到最优的控制效果，同时不需要额外增加传感器的种类。于是，建立如下控制律：

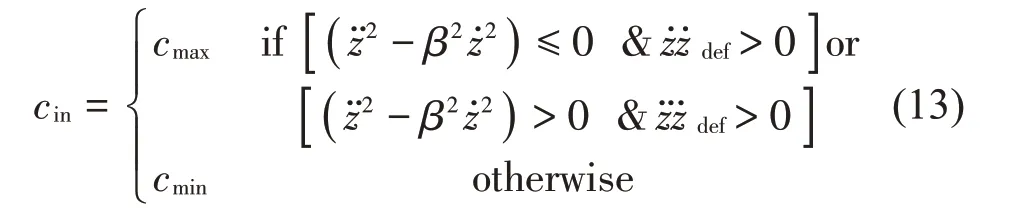
其中：cin是可变减振器阻尼系数和分别代表车身垂向速度、悬架偏转速度和车身垂向加速度，cmin和cmax为最小和最大阻尼系数。根据天棚理论[13]一般取cmax=csky，cmin一般通过主观感受进行标定获取。

由式（13）可以看出：在每个采样时间间隔内，如果-˙＞0，则选择加速度控制方法，这时车身加速度与悬架偏转速度方向如果相同，cin取最大值cmax，方向相反，cin取最小值cmin；如果-˙≤0，则选择天棚控制方法，这时车身速度与悬架偏转速度方向如果相同，cin取最大值cmax，方向相反，cin取最小值cmin。()-可以被当作频率范围选择开关，其中β∈R+为频率切换系数，在机车悬架控制中，一般取β=19 rad/s，此时切换频率为3 Hz。当减振器作动频率小于3 Hz时，切换为天棚控制，当频率大于3 Hz时，则切换为加速度控制。天棚加速度混合控制方法根据频率切换系数，能够自适应选择天棚算法对低频振动进行控制和选择加速度算法对高频振动进行控制，进而改善车辆垂向振动水平。

将SH-ADD 控制策略作用于整车动力学模型，则其控制量为

令控制阻尼力为Ud=[UdflUdfrUdrlUdrl]T，阻尼系数ccontrol=[cflcontrolcfrcontrolcrlcontrolcrrcontrol]T，减振器作动速度为有

2.2 车身姿态补偿控制

SH-ADD控制策略仅是对车辆垂向运动进行控制，当车辆处于加速、制动或转向工况时，由于存在运动惯性，车身会发生俯仰、侧倾运动，使乘员产生不舒适感。因此，本文在上述算法的基础上，建立车身姿态补偿控制，根据传感器数据计算车身的俯仰、侧倾角加速度，并将其等效作用于四支减振器处进行阻尼力补偿。这种自适应阻尼控制系统（Adaptive Damping System，缩写为ADS）不仅可以降低车辆垂向运动的振动水平，还可以提升车辆的抗俯仰及侧倾效果，使其控制效果更加接近于主动悬架。

在行驶工况不太恶劣情况下，可以认为轮胎始终接地。分别选取左前悬架动挠度值与平衡位置动挠度传感器值之差s01、右前悬架动挠度值与平衡位置动挠度传感器值之差s02、左后悬架动挠度值与平衡位置动挠度传感器值之差s03。设车辆轴距L=lf+lr、前轮距为wf、后轮距为wr、前悬簧上质量为mf、后悬簧上质量为mr。

侧倾角加速度近似为

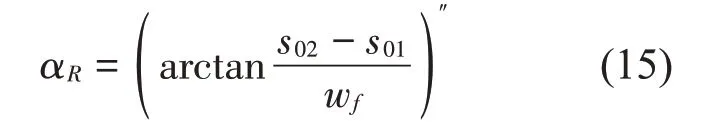
于是抗侧倾的左侧悬架等效侧倾补偿力为

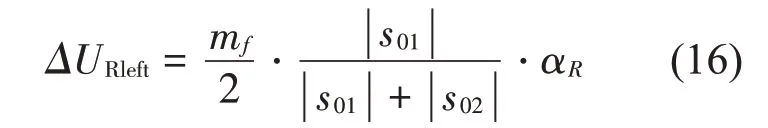
抗侧倾的右侧悬架等效侧倾补偿力为

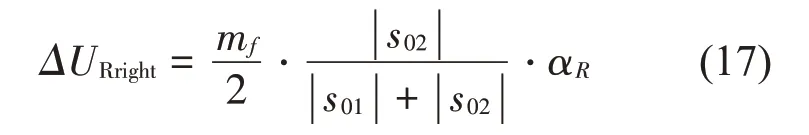
同样地，得到当前俯仰角加速度近似为

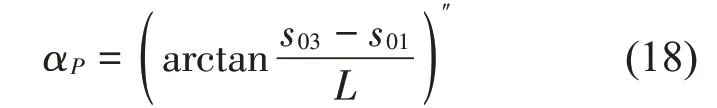
抗俯仰的前悬架等效补偿力为

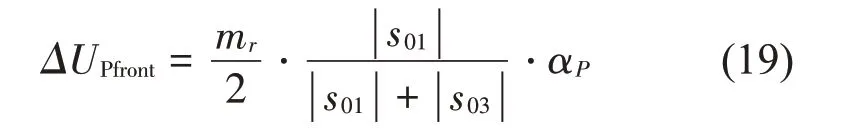
抗俯仰的后悬架等效补偿力为

进行车身姿态补偿控制时根据侧倾角加速度与俯仰角加速度实时计算出等效侧倾补偿力与等效俯仰补偿力，根据驾驶员操纵车辆的运行工况能够自适应调节阻尼增大或减少，进而提高车辆运行的稳定性。

综上，经过天棚加速度控制、车辆抗俯仰及侧倾补偿控制修正后的自适应阻尼力值为

式中：U=[Ufl Ufr Url Url]T为修正后的阻尼力值，UR=[ΔURleftΔURright]T，UP=[ΔUPfrontΔUPrear]，M和N值如式(22)所示：

通过查表的方式，控制系统输出当前状态下需求阻尼力对应的电流值，其数据来源为可调阻尼减振器的U-I-v特性，可通过减振器台架测试获取，有：

式中：Uo为Ufl、Ufr、Url、Urr其中之一，且Io与之对应。

3 试验台架搭建

为了验证外置电磁阀可调阻尼减振器以及控制策略的有效性，搭建减振器机械硬件在环试验台，验证了在真实减振器工作状态下不同车速不同路面下控制算法对整车驾乘舒适性与操纵稳定性的影响。

减振器机械硬件在环试验台（mHIL）主要包括：车辆动力学模型、实时仿真模拟系统(RTS)加载台架和相应的控制器、被测样件及实现系统集成的一套应用软件。该系统主要由硬件及软件两部分组成，试验框架如图2所示。系统软件部分由测试管理平台、车辆动力学模型及控制策略等组成。硬件系统部分由2台上位机控制电脑、1个dSPACE仿真器、1个MTS试验台控制器、4个MTS减振器试验台以及4个电磁阀式减振器及1个电流放大器等组成。dSPACE仿真器主要包含：

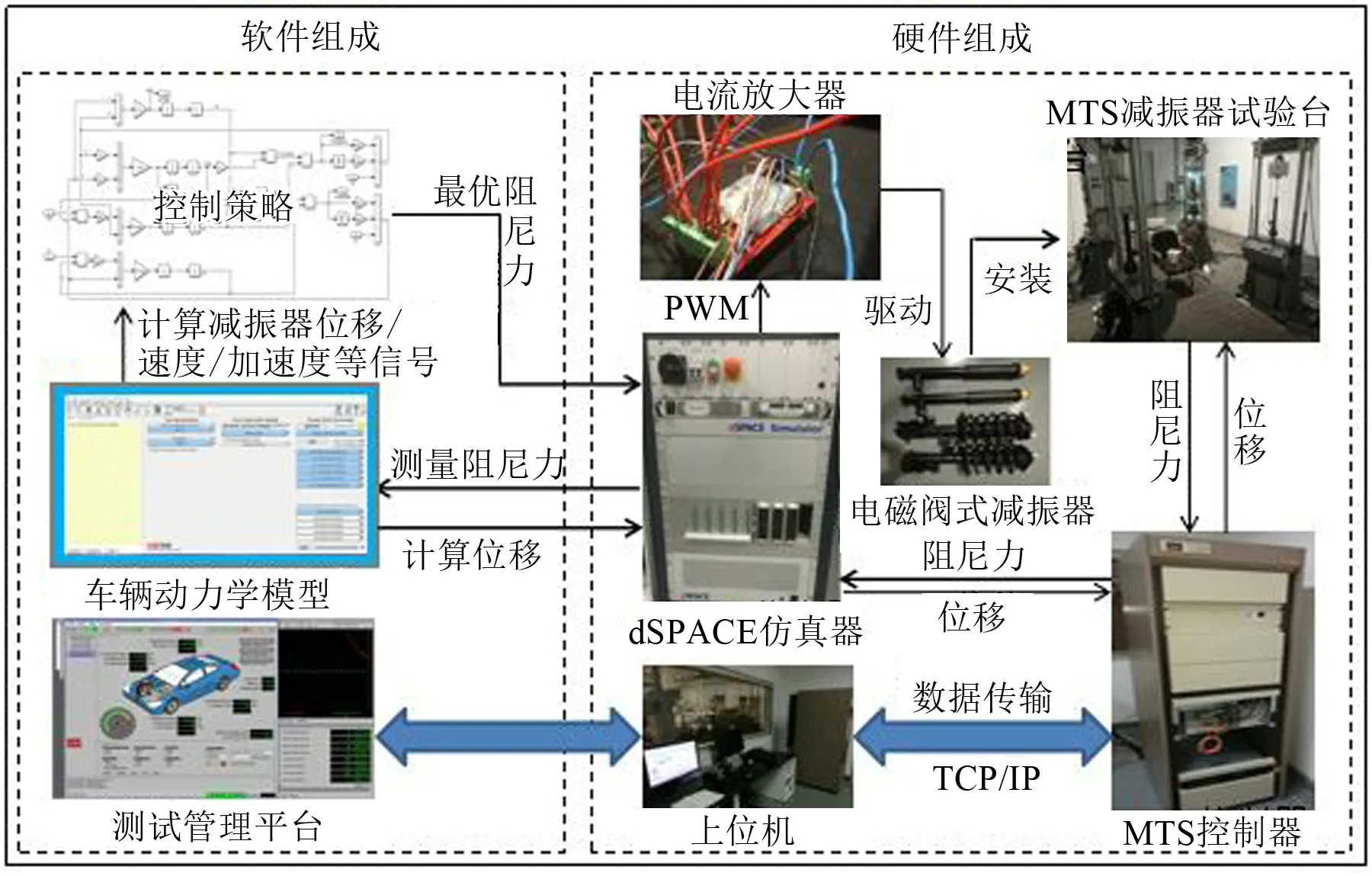
图2 减振器机械硬件在环试验框架图

（1）飞思卡尔Power PC750GX处理器、主频高达1GHz的DS1005处理器板卡；

（2）DS2202 多功能输入输出信号采集板卡，该板卡集成16路AD（模数转换）输入采集接口和20路DA(数模转换)输出接口；

（3）DS4302 CAN 信号传输板卡等。电流放大器主要采用基于PWM 控制的BUCK 驱动电路，基本原理是通过高边驱动芯片控制NMOS 管通断形成高压PWM 功率输出，将控制系统输出电流信号由最大值50 mA提高到2 A，以驱动电磁阀开关控制减振器阻尼力改变。

4 试验研究

本节主要介绍使用第3节所搭建的试验台架对第2节中提出的控制算法进行有效性验证。所用整车模型的参数如下：ms=1 775 kg，mf=1 084 kg，mr=691 kg，mufl=mufr=52.2 kg，murl=murr=34.6 kg，Ix=830 kgm2，Iy=3 684 kgm2，ksfl=ksfr=31 000 N/m，ksrl=ksrr=65 000 N/m，ktfl=ktfr=ktrl=ktrr=220 000 N/m，lf=1.05 m，lr=1.7 m，wf=wr=1.615 m。

4.1 垂向运动台架试验结果

随机路面被用来作为半主动悬架系统垂向运动的激励源。本文采用谐波叠加法重构路面不平度[21]，随机路面的路面谱表达式为

式中：pi代表空间频率，pmid-i为区间的中心频率，Hq(pmid-i)为对应的功率谱密度，ψ表示正弦函数的相位（deg），x表示路面长度（m）。

按照标准GB/T7031－2005的规定，B级和C级功率谱密度函数值Hq(p0)分别取为64×10-6m3和256×10-6m3，各区间内Hq(pmid-i)取值分别按照标准中B级和C级路面1/3倍频程中心频率对应的位移功率谱密度平均值确定，利用上述方法构造的B级和C级路面如图3所示。

图4至图5列出了车速在60 km/h时在B级路面和C级路面下ADS 和被动悬架的质心加速度频域曲线对比。表2列出了在不同车速不同路面下ADS与被动悬架台架试验结果。从图表中可以发现所设计的控制算法与被动悬架相比在B级路面不同车速下质心加速度幅值平均降幅达21.16%，在C级路面不同车速下质心加速度平均降幅达13.21%。

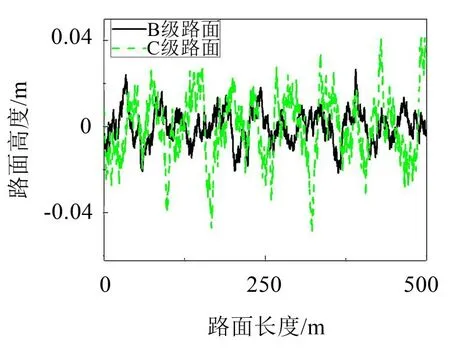
图3 B级和C级路面示意图

4.2 纵倾工况台架试验结果

根据国标GB 21670－2008《乘用车制动系统技术要求及试验方法》，在试验台架上设置车辆以80 km/h 初速度匀速行驶，然后紧急制动直到汽车停止，得到不同减速度下俯仰角的变化曲线，如图6所示。另外，设置加速度从0 km/h增加到120 km/h的不同试验工况，测量俯仰角的变化曲线，如图7所示。表3列出了在不同纵向工况下ADS与被动悬架车身俯仰角性能对比。

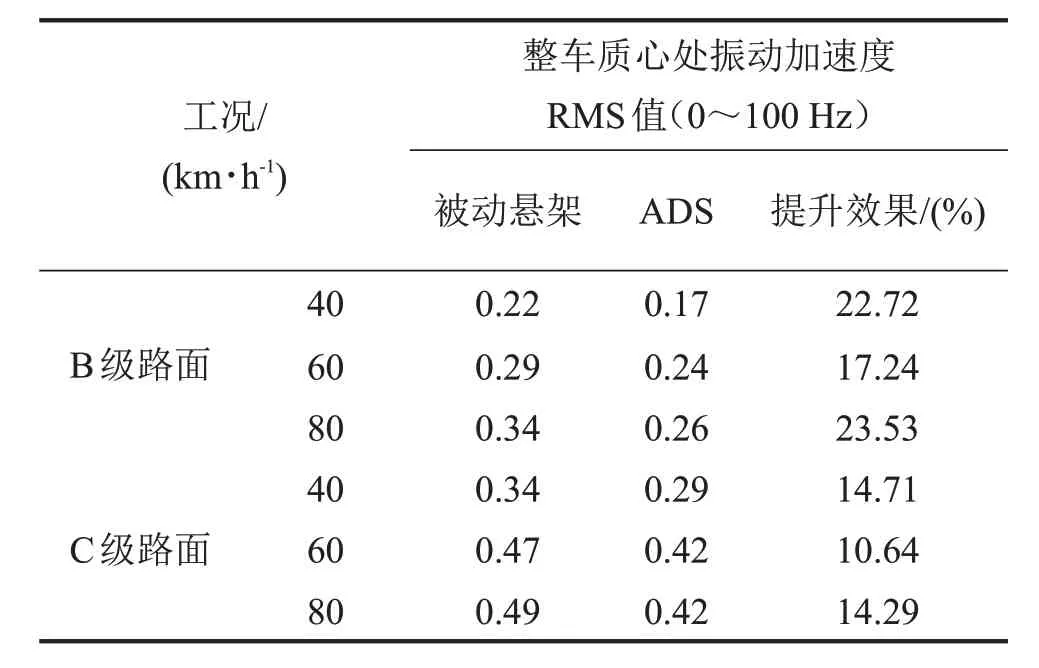
表2 不同路面不同车速下质心加速度试验结果/g

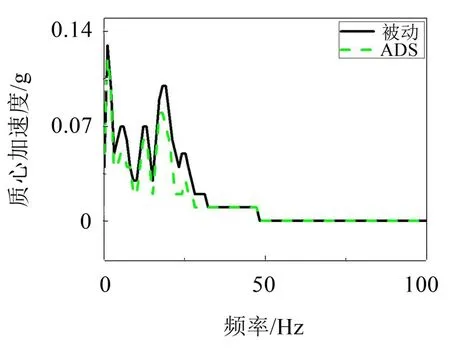
图4 车速为60 km/h时B级路面下质心加速度频域对比图

从表3中可以得出，设计的控制算法与被动悬架相比在不同减速度下俯仰角波动峰峰值平均降幅达25.50%，在不同加速度下俯仰角波动峰峰值平均降幅达28.82%。

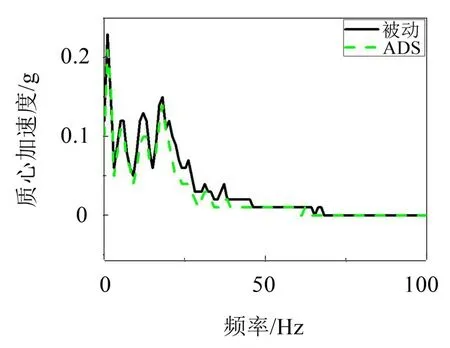
图5 车速为60 km/h时C级路面下质心加速度频域对比图

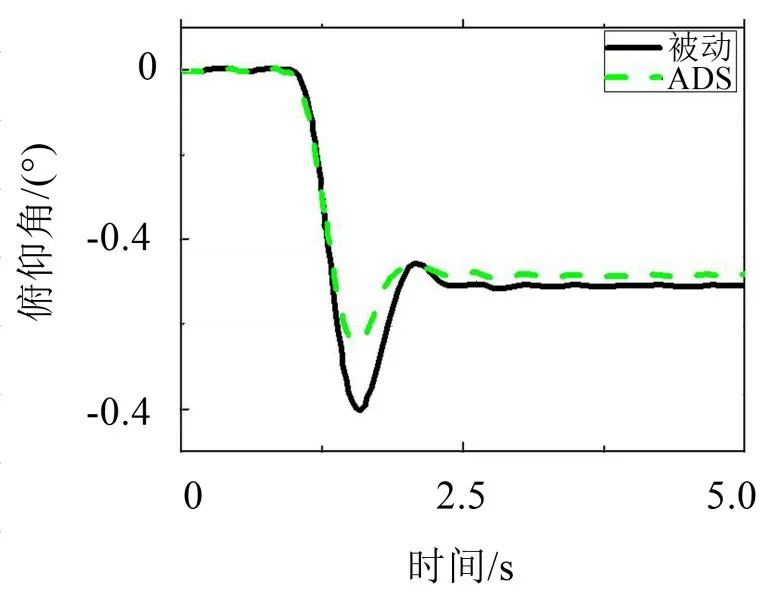
图6 减速度为0.2 g时车身俯仰角时域对比图

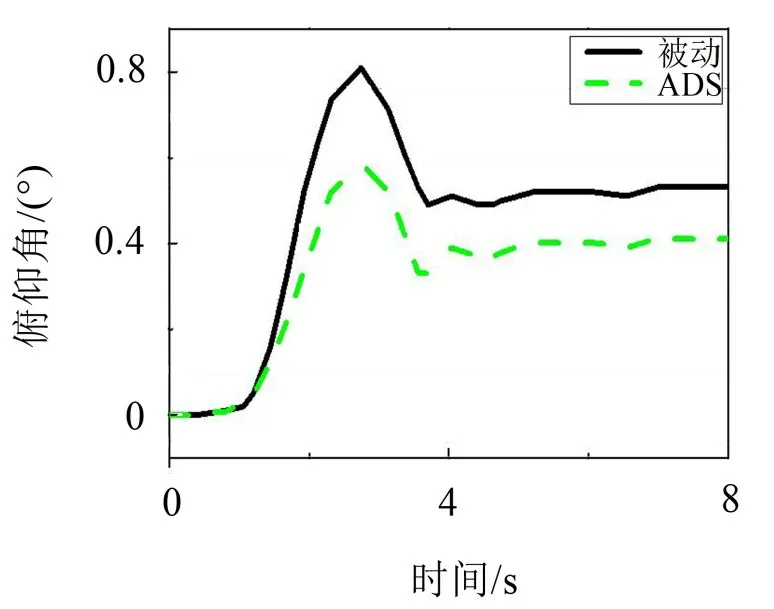
图7 加速度为0.2 g时车身俯仰角时域对比图

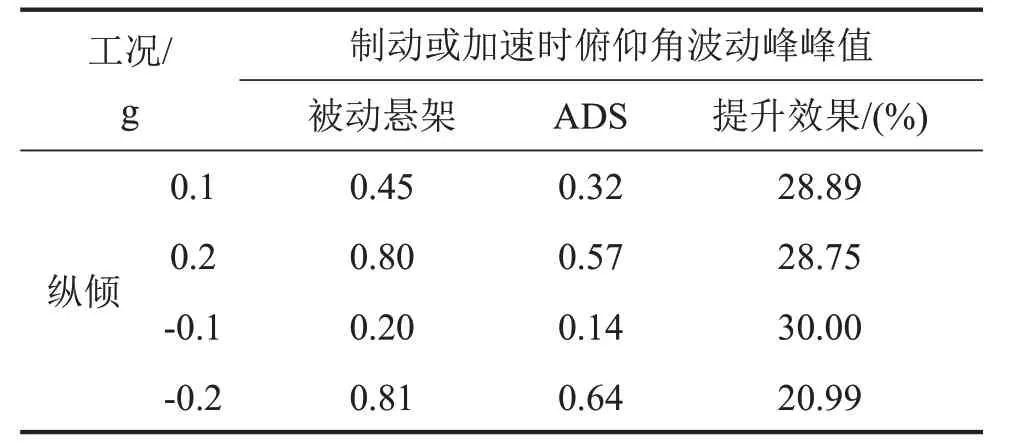
表3 不同纵倾工况下车身俯仰角试验结果/(°)

4.3 蛇形工况台架试验结果

根据GB/T 6323－2014《汽车操纵稳定性试验方法》，在试验台架上设置蛇形工况，车辆分别以50 km/h、55 km/h和60 km/h车速匀速通过试验路段，记录车身侧倾角的变化曲线，如图8所示。表4列出不同车速蛇形工况下ADS与被动悬架之间的性能对比。

从表4中可以发现，设计的控制算法与被动悬架相比在不同车速下侧倾角幅值均有所降低，最大达到4.78%，最小为1.77%。虽然从客观数据百分比来看车身侧倾角峰值降幅不大，但是该指标的降低对操纵稳定性主观评价影响较大。

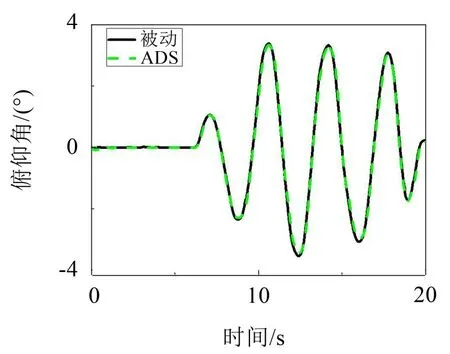
图8 车速为60 km/h时蛇形工况下车身侧倾角时域对比图

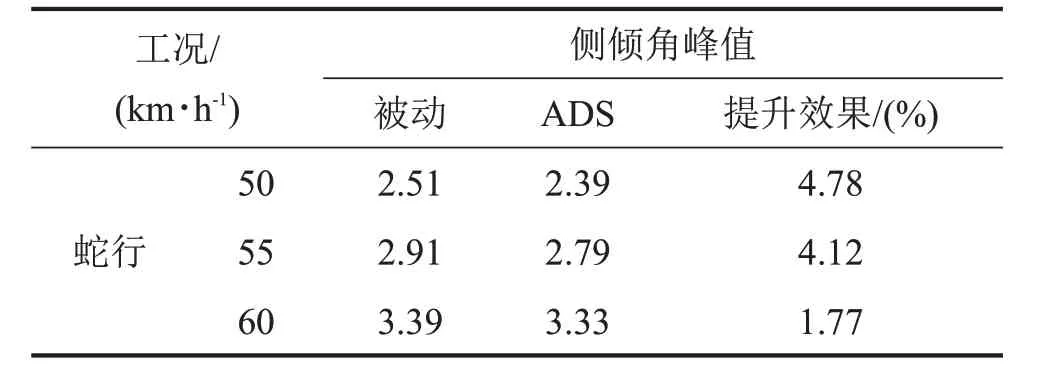
表4 不同车速蛇形工况下车身侧倾角试验结果/(°)

5 结语

本文提出了一种基于车身姿态补偿控制与天棚加速度控制相结合的算法，建立了自适应阻尼控制系统，并基于此计算出半主动悬架系统最优阻尼力，进而优化车辆驾乘舒适性与操纵稳定性。与被动悬架相比，该算法在不同路面、不同车身姿态变化下都取得了不错效果。主要结论如下：

（1）天棚加速度控制算法主要是对垂向运动进行控制，通过试验结果表明其可以在全频域降低车辆振动水平，B级路面不同车速下质心加速度幅值平均降幅达21.16%，C级路面不同车速下质心加速度平均降幅达13.21%。将该算法与车身姿态补偿控制相结合，可同时兼顾对车辆纵向及侧向运动姿态进行控制，使其控制效果更加接近主动悬架。

（2）本文搭建了一种基于整车动力学模型的机械硬件在环仿真试验台，通过该台架不仅能验证半主动悬架系统的垂向控制效果，还能对俯仰以及侧倾工况进行试验验证，丰富了半主动悬架系统开发的试验手段，可以在无实车条件下对控制算法进行验证，缩短了项目开发周期。