周期声学黑洞结构弯曲波带隙与振动特性

李 敬，万志威，李天匀,3，朱 翔,3

（1.华中科技大学 船舶与海洋工程学院，武汉430074；2.船舶和海洋水动力湖北省重点实验室，武汉430074；3.高新船舶与深海开发装备协同创新中心，上海200240）

声学黑洞(ABH)是通过幂律裁剪结构来实现结构阻抗的渐变，引起结构弯曲波相速度与群速度的变化，从而实现波的能量聚集与操控。在梁或薄板中，若厚度变化为h(x)=εxm(m≥2)，则弯曲波波速会随着厚度减小而减小[1]。很多研究[2-5]表明敷设阻尼的黑洞对于抑制结构振动或降低声辐射能达到更好的效果，之后有学者[6]指出此为综合阻尼层的阻尼与刚度效应，在黑洞中心1/4长度内敷设阻尼材料效果最佳。

但是声学黑洞的应用也存在不足，Conlon 等[7]计算了带阻尼的声学黑洞结构的辐射声功率，其结果显示在1 000 Hz以下时效果与不带声学黑洞结构响应相似，表明声学黑洞作用频带存在截止频率，低于该频率时声学黑洞作用效果较小。Li等[8]研究了声学黑洞梁的振动与声辐射效应，结果也体现出声学黑洞的截断效应。并指出适当增加黑洞长度可以增强黑洞对低频作用的效果。

目前声学黑洞向低频带拓展的方式主要有非线性与周期性排列两种。Gusev 等[9]考虑微观非均匀材料的非线性对声学黑洞板中的弯曲波的影响，发现非线性吸收随着波幅的减小而逐渐消失，导致大多数声学黑洞中的声波完全衰减。周期性排列[10-12]则是通过多个黑洞的组合达到拓宽频带的作用，声学黑洞属于变截面结构，其周期性排列已经属于声子晶体的范畴。通过合理设置黑洞参数与排列方式以及材料的分布等可以得到结构对应的带隙特性。但这方面的研究仍很匮乏，本文研究了周期性分布的声学黑洞结构，选择合适的晶胞对弯曲波能带结构进行了分析并对有限周期的声子晶体梁振动传递特性进行分析，在较宽频带内得到了弯曲波带隙，与等长度的恒定截面梁及周期楔形梁相比，振动位移传递曲线在带隙区间出现极大衰减。并且通过改变黑洞区域材料分析了黑洞与基体材料差异对能带的影响，为采用声学黑洞梁抑制振动向低频带拓展提供一定思路。

1 声学黑洞声子晶体梁

1.1 声学黑洞中的弯曲波

当弹性波在声学黑洞中传播时，波位移w(x)可以由式(1)描述：

式中：B(x)是x处的波幅k(x)为波数。

实际应用中黑洞必然存在截断[13]，存在截断厚度h0，厚度h(x)=εxm+h0，则相应波数k(x)为

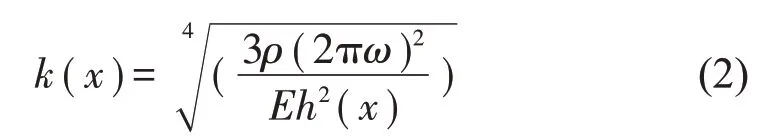
式中：ρ、E、ω分别表示黑洞结构密度、杨氏模量与角频率。

1.2 声子晶体能带结构与传输特性

Bloch 波中电子能量的特征值问题中包含了电子能量与波矢之间的关系，常出现没有波矢与能量对应区域,称之为带隙。而两者之间的关系称之为能带结构[14]。不计体力条件下，弹性波在具有晶格周期性的介质中自由传播时特征方程为

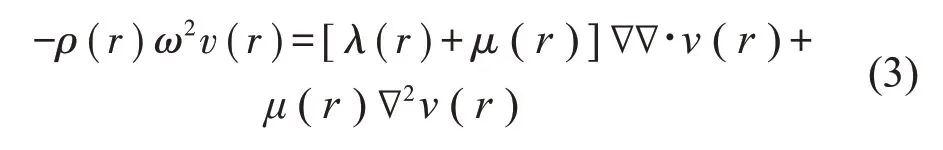
式中：ρ、λ、μ分别为结构的密度、lame参数与剪切模量，v为位移函数，均为位置r的函数。

满足式(3)解的波称为Bloch波，可表示为

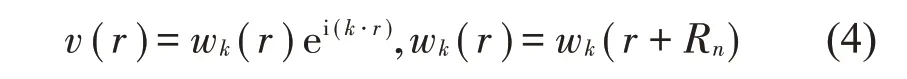
式中：Rn为正格矢。

周期性梁弯曲波表达形式为

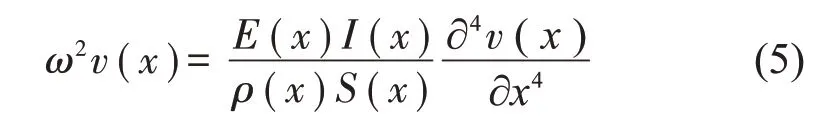
式中：E、ρ、I、S分别为结构杨氏模量与密度、截面惯性矩与面积，均为位置坐标的周期函数。

其位移解满足：

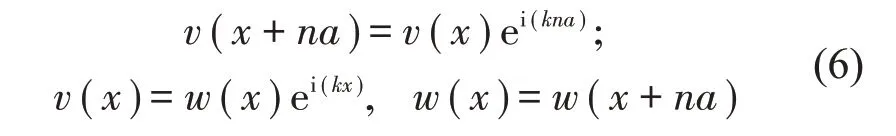
式中：a为晶格常数，n为周期数。

故周期性梁中传播的弯曲波属于Bloch 波，将波函数代入弹性波动方程得到波矢与频率之间关系，即频散关系，但是在声子晶体中也继续沿用了能带结构的概念[15]。

无限周期声子晶体梁带隙内弯曲波完全被屏蔽，能带结构足以描述声子晶体的特性。而有限周期结构中带隙内弯曲波传递表现为衰减而非完全无法传播，即带隙内部分弯曲波仍能传播，此时需要获得结构参数如位移、速度、加速度的传递函数。将传递函数与能带结构结合进行分析。

但由于激励与响应幅值数量级的差异，振动与声学中通常采用如下定义的传递函数[16]，振动中称之为振级落差：

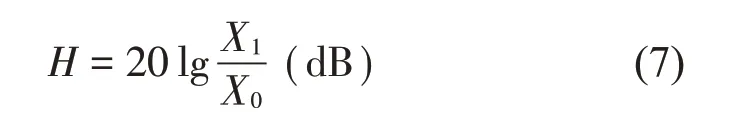
式中：X1为响应，X0为输入，可以是位移、速度或加速度。

1.3 能带结构的计算方法

计算声子晶体结构带隙特性的方法通常有3种：传递矩阵法、平面波展开法和有限元法。

采用传递矩阵法计算声子晶体梁可得到精确解，对于计算不同材料恒定截面的梁较为简单。其原理在于利用变截面处或变材料处的弯曲受力与变形的关系建立传递矩阵，并利用声子晶体周期性得到波矢与频率之间的关系。但对于由声学黑洞构成的声子晶体梁，其截面的变化是渐变的，利用传递矩阵法时，该方法并不太适用。

平面波展开是将弹性波展开成一系列平面波，在倒格矢空间将波动方程转化为特征值方程进行计算，但是计算严重阻抗失配的声子晶体收敛慢。对于声学黑洞渐变变截面的计算，以及本文所考虑的较大阻抗失配问题，平面波展开法存在一定局限性。

有限元法对于计算含有声学黑洞这种复杂截面的声子晶体梁有着很好的优越性和收敛性。计算能带结构时，通过将Bloch 位移波作为常规有限元法的位移解，设置周期性边界条件，改变波数计算固有频率即可得到结构的频散关系。

一维声子晶体晶胞中任一点Q位移为

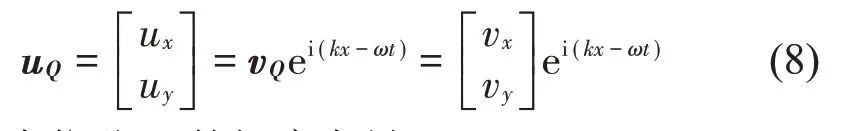
式中：vQ为位移uQ的幅度向量。

则对应晶胞中单元节点位移uie为

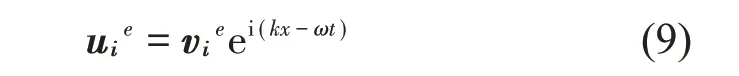
式中：vie为位移uie的幅度向量。

有限元法中将单元中任一点位移用所在单元节点位移进行插值：

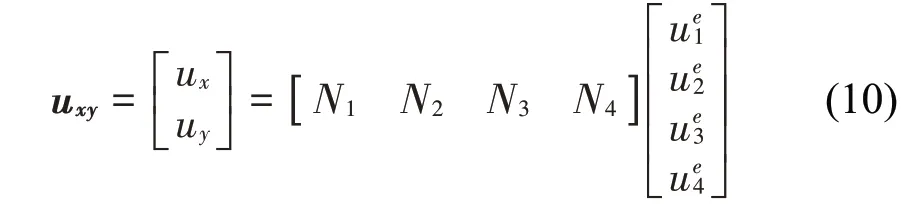
将式(9)代入式(10)，得到单元任一点位移：

式中：

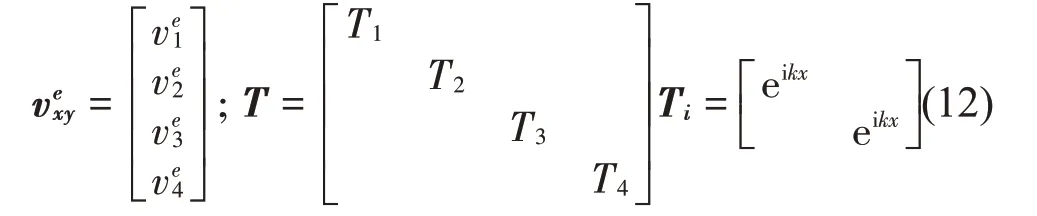
将式(11)代入单元平衡方程：

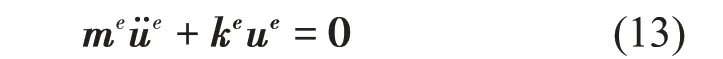
得到晶胞的单元平衡方程：

式中：ke与me为单元整体刚度矩阵与质量矩阵。

通过整体组装矩阵，得到整个系统的特征值问题为

式中：K与M为系统整体刚度矩阵与质量矩阵；v为系统位移幅值列向量。

因此采用有限元法计算声学黑洞声子晶体梁的能带结构时，只需要选取一个晶胞单元，设置弗洛奎特周期性边界条件。将波矢限制在第一布里渊区，通过计算晶胞的固有频率即可得到结构的能带结构图。故本文通过COMSOL 软件采用有限元法对周期排列的声学黑洞结构的带隙特性与传输特性进行分析。

2 有限元模型

2.1 晶胞模型

对于周期性声学黑洞梁，声学黑洞之间通常有一定间隔t。Tang 在文献[5]中指出在黑洞中心1/4区域敷设阻尼层能较好提升黑洞抑制波传播的效果，因此选择黑洞与基体的组合作为声子晶体梁的晶胞结构，并在黑洞中心1/4 区域敷设厚度为1 mm的阻尼层材料。

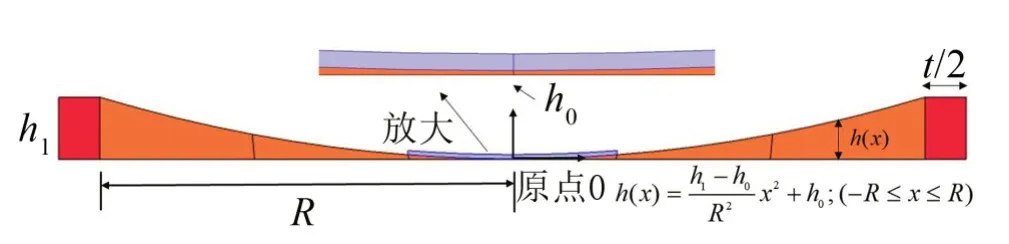
图1 声学黑洞梁晶胞模型

基体长度为间距t的1/2。t=20 mm，整体宽度B=50 mm，为矩形截面。如图1所示，橙色区域为黑洞，红色部分为基体，蓝色部分为阻尼层。当构成无限周期时，此结构构成一维声子晶体。

王博涵等[17]选取黑洞长度R=100 mm，幂指数m=2，对单个黑洞薄板进行振动特性分析，结果表明单个黑洞抑制结构振动有较好的抑制效果。本文将该文献选取的参数作为参考，选取黑洞长度为R=100 mm、幂指数m=2的声学黑洞进行分析。厚度取为h1=15 mm，考虑声学黑洞最薄处不可能无限趋于0，选取截断厚度为1/100的梁厚度，即黑洞最薄处厚度h0=0.15 mm。选取黑洞最薄处为原点O，则黑洞表达式为

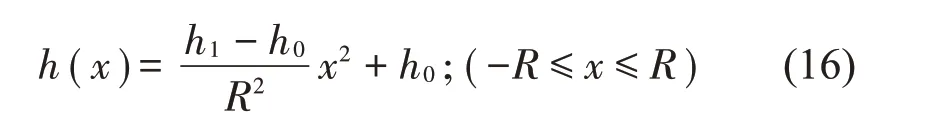
代入具体参数，即：

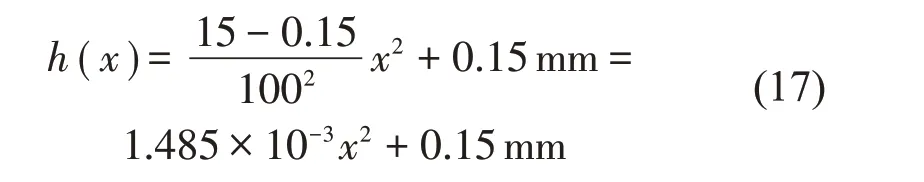
因此晶格常数为：a=2R+t=220 mm。

晶胞有限元网格模型如图2所示，阻尼层采用一层的映射四边形网格，宽度方向为1 mm，黑洞区域采用自由四边形网格，最小网格边长为0.15 mm，最大边长为1.875 mm。基体部分采用映射的四边形网格，尺寸大小为1.875 mm×2 mm。

图2 声学黑洞晶胞有限元模型

为对比分析周期黑洞结构的振动波抑制效果，对具有同样截面尺寸的矩形截面梁也进行对比分析，其与黑洞晶胞等长的几何模型与有限元模型如图3与图4所示，网格采用映射四边形网格，尺寸为1.875 mm×2 mm。与声学黑洞梁相比，仅将黑洞区域替换成与基体等截面的截面梁,当此部分区域材料不同时，这也构成一种声子晶体。

图3 恒定截面梁几何模型

图4 恒定截面梁网格模型

2.2 有限周期结构模型

实际中周期性声学黑洞梁不可能具有无限周期，因此选取8个周期晶胞构成的声学黑洞梁与恒定截面梁，进行弯曲振动传递特性分析，几何模型分别如图5与图6所示。有限元模型划分尺寸大小与晶胞有限元模型一致，仅做8个周期的阵列。

图5 8周期声学黑洞梁模型

图6 8周期恒定截面梁模型

3 带隙特性与传递特性分析

对于无限周期的声学黑洞结构，利用有限元法对晶胞进行分析，通过在晶胞两端设置弗洛奎特周期性边界条件，限制波数k在第一布里渊区内，波数步长为计算不同波数下结构的固有频率，得到波数与频率之间的关系，即能带结构。

对于8个周期的不同结构，取长度L=8a=1 760 mm，在梁一端沿宽度方向施加大小为1 N/m的垂向分布力。在梁的另一端提取位移响应，频率范围为5 Hz～4 000 Hz，步长为5 Hz。选取输入端与输出端的位移响应的均方值计算传递函数，进而得到传递函数频响曲线，具体处理方法如下：

有限元法中，通过网格在线与面上划分出多个节点。设输出端N个节点的位移响应幅值分别为s1、s2、…、sN。

则输出端平均位移响应为

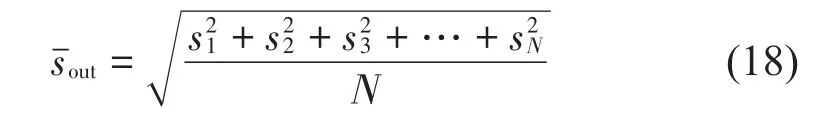
通过同样的方法得到输入端上均方位移响应，则位移传递函数H为

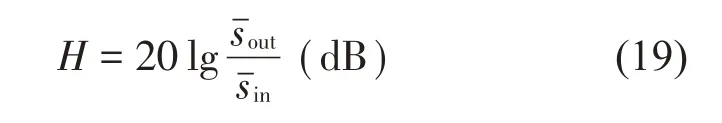
3.1 钢质黑洞嵌入钢质基体

首先考虑基体与黑洞材料同为钢时的带隙特性与传递函数特性。具体结构参数见表1。

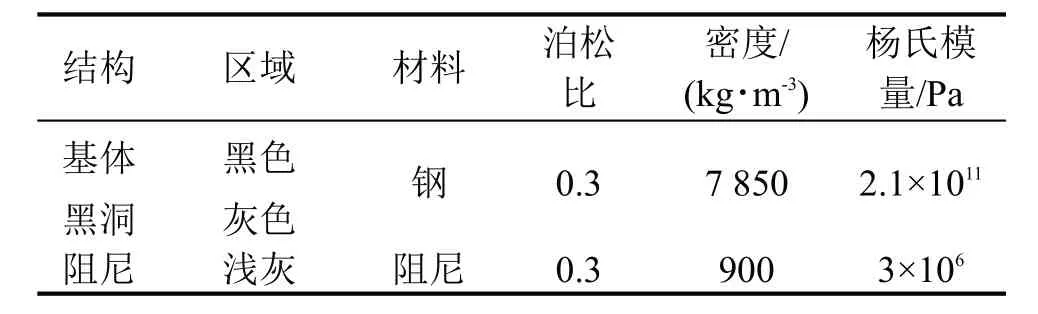
表1 结构材料参数

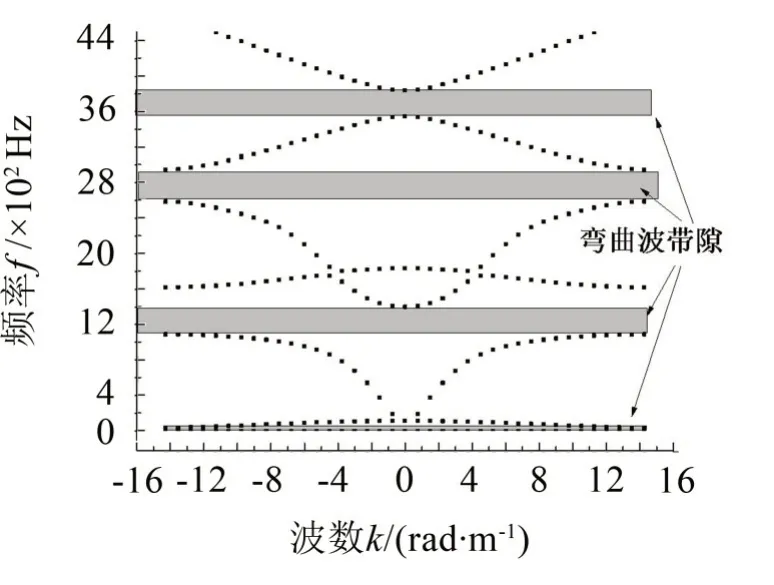
图7 钢质黑洞梁弯曲波能带结构图

声学黑洞声子晶体梁晶胞弯曲波能带结构如图7所示，根据带隙图能较清晰看出带隙的分布与宽窄，为了具体比较带隙区间的频率范围，将带隙区间列入表中，如表2所示，同时引入归一化宽度[18]的概念：

式中：f1与f2分别为带隙截止频率与起始频率。

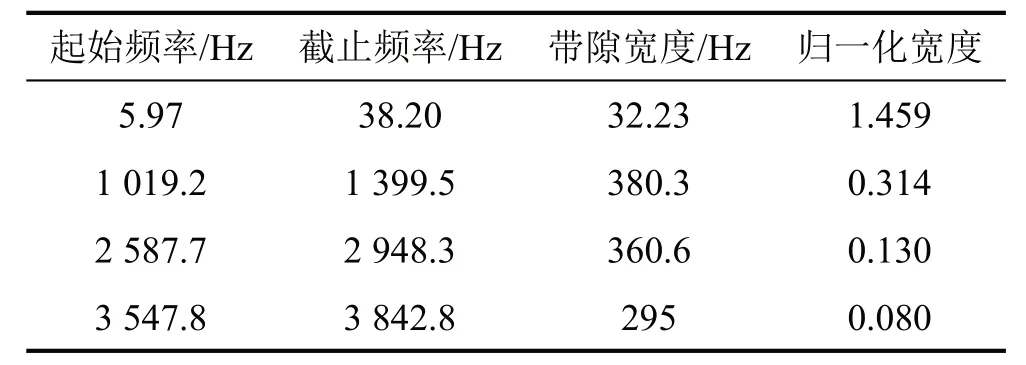
表2 通过晶胞得到的弯曲波带隙特性

图8给出了8个周期声学黑洞梁与等长度的恒定截面梁的位移传递函数曲线。以0 dB为阈值，声学黑洞梁带隙区间（灰色阴影部分）的位移传递函数出现很大衰减，每个带隙区间最大衰减都达到35 dB以上，效果显著，进一步验证了声学黑洞构成的声子晶体梁存在弯曲波带隙。而恒定截面梁位移传递特性则在阈值线附近振荡，表明不存在带隙特性。

将得到的此带隙区间与通过晶胞计算得到的带隙进行比较，如表2与表3所示，可以看出两者的带隙区间大致一致，带隙宽度与归一化宽度差异较小。但是带隙区间起止频率有一定的差异。这一部分主要是无限周期结构和有限周期结构的差异。

从整个频段看，声学黑洞梁传递衰减明显优于恒定截面梁。除了带隙区间外，在带隙区间附近的频带（黑色阴影部分），周期声学黑洞梁传递也出现较大衰减，如85 Hz 至400 Hz 频带最大衰减达到30 dB。这可以从能带结构图中得到解释，虽然这些区间没有对弯曲波形成完全禁带，但是由于在黑洞区域传播时弯曲波数是随截面变化的，这些部分抑制了部分波数传播的弯曲波，因此在传递响应图中也出现较大衰减。

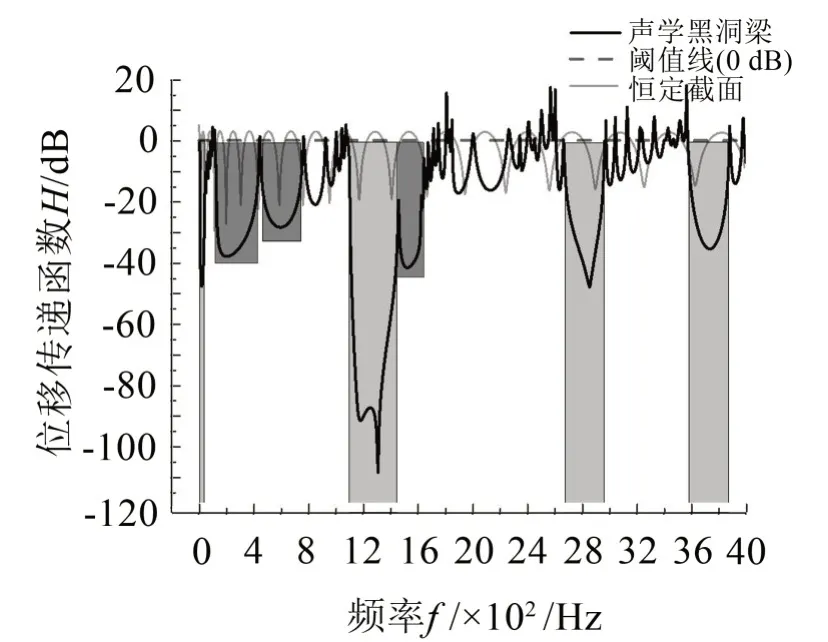
图8 钢质黑洞梁振动位移传递函数

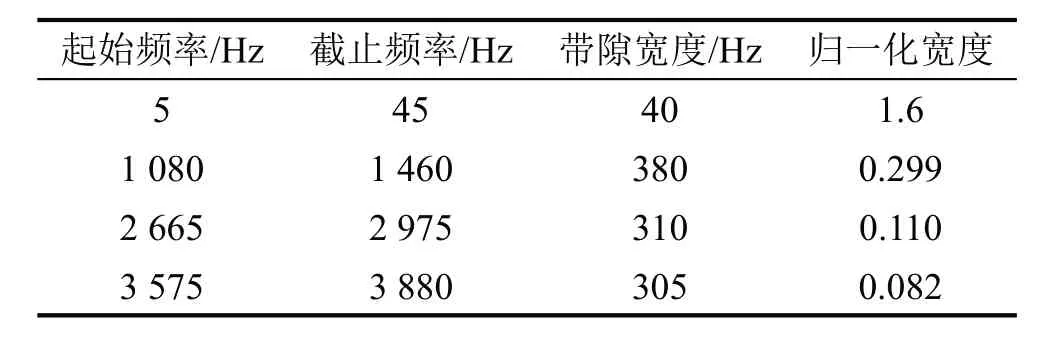
表3 根据传递函数确定的弯曲波带隙

为了分析周期声学黑洞梁中周期结构与声学黑洞对抑制结构振动的贡献，选取与钢质周期声学黑洞梁等长度的单黑洞梁进行对比分析。黑洞参数保持不变，为保证长度一致，非黑洞部分取为恒定截面梁，如图9所示。

图9 等长单黑洞梁模型

在靠近黑洞梁一端进行激励，另一端提取位移响应，得到位移传递函数曲线如图10所示。从图中可以看出周期黑洞梁在带隙区间（灰色阴影）抑制振动效果明显优于等长度的单黑洞梁，非带隙区间内两者抑制振动效果差别较小。这说明周期性结构对于形成带隙区间从而有效抑制结构振动传递起着显著作用，但是作为由变截面的单黑洞组成的结构不能产生带隙区间。

为了进一步研究声学黑洞对于采用周期声学黑洞梁抑制结构振动的效果，将黑洞替换为楔形梁，计算等长度的8周期的钢质周期楔形梁的位移传递响应，同样在中心1/4 区域敷设阻尼，其结构如图11所示。

截面厚度表达式为

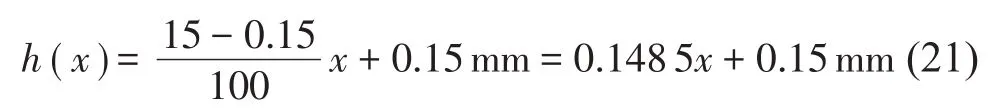
从图12所示周期楔形梁与周期黑洞梁的位移传递响应对比中可以看出，黑洞梁在[5，45]Hz、[1 080，1 460]Hz与[2 665，2 975]Hz 频带内明显削弱了结构振动的传递，而楔形梁在[25，285]Hz频带内较大削弱振动位移的传递，即周期黑洞梁抑制振动的频带范围明显优于周期楔形梁，声学黑洞与周期排列的共同作用使得周期声学黑洞梁产生了较好的带隙特性。这也从侧面说明周期性结构是形成带隙的必要条件，选择合适的原胞才能使结构的带隙特性更加明显，从而更好抑制结构振动，而声学黑洞可作为声子晶体的一种良好的原胞。

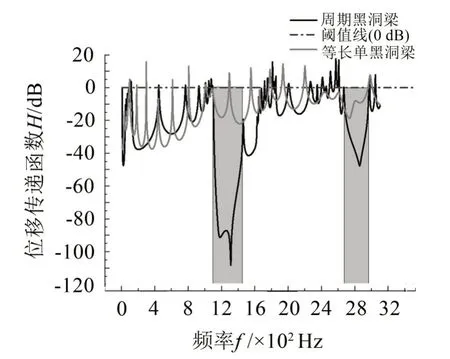
图10 单黑洞梁振动传递函数

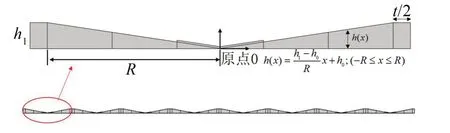
图11 周期楔形梁及其组成单元

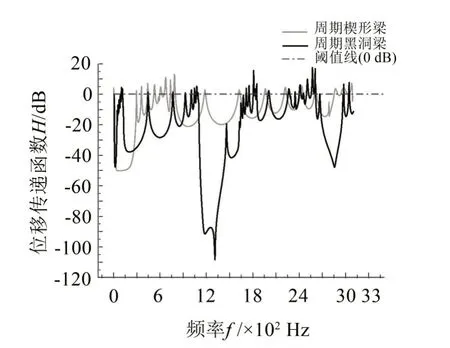
图12 周期楔形梁振动位移传递函数

3.2 铝质黑洞嵌入钢质基体

材料特性差异的周期性排列是声子晶体研究的另一思路，为此将黑洞区域材质更换为铝，不改变基体材料。作为对比的恒定截面梁，中间段材料也变换为铝。铝材料参数见表4。

表4 铝材料参数

声学黑洞声子晶体梁结构的弯曲波能带结构如图13所示。对应得到铝质黑洞嵌入钢基体的弯曲波带隙见表5。对比表2可知，铝制黑洞嵌入钢质基体的带隙相较于钢质黑洞而言，整体向低频移动。

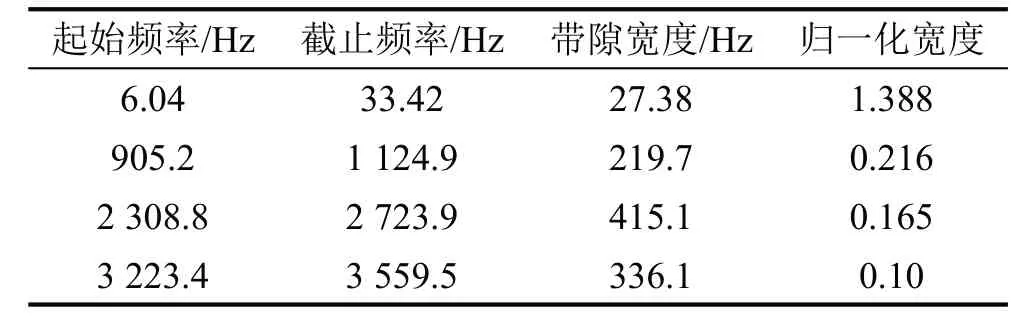
表5 铝质黑洞梁弯曲波带隙特性

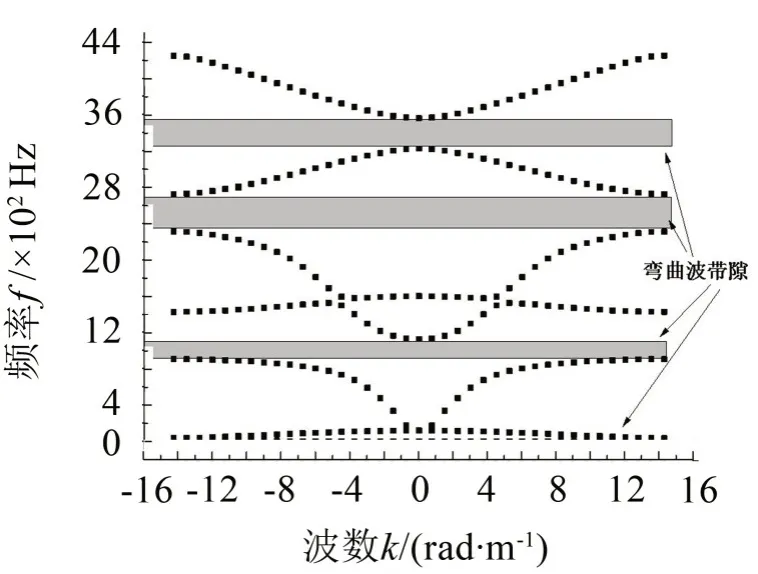
图13 铝质黑洞梁弯曲波能带结构图

位移传递特性曲线如图14所示，响应曲线中对应带隙区间（灰色阴影部分）的弯曲振动传递出现极大衰减，在相应的带隙区间附近某些频带（黑色阴影）传递响应也同样出现较大衰减。相较于由铝制恒定截面嵌入钢基体梁而言，声学黑洞梁传递特性衰减优势明显，进一步佐证了3.1节中的结论。

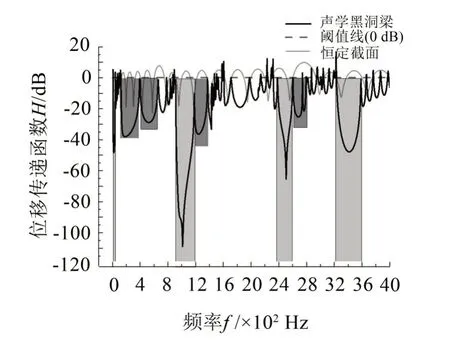
图14 铝质黑洞梁位移传递函数

3.3 环氧树脂黑洞嵌入钢质基体

为了进一步验证3.2节中的结论，将铝质黑洞替换成与钢基体阻抗失配更大的环氧树脂材料进行分析。环氧树脂具体参数见表6。

表6 环氧树脂材料参数

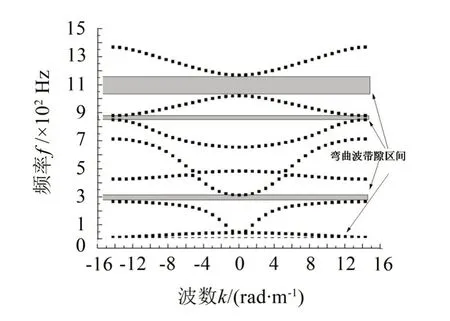
图15 环氧树脂黑洞梁弯曲波能带结构图

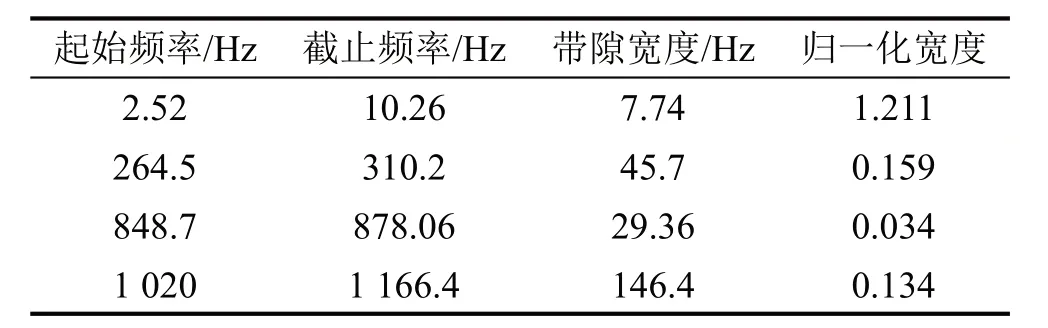
表7 环氧树脂黑洞梁弯曲波带隙特性

图15给出了环氧树脂声学黑洞梁弯曲波能带结构。其带隙起止频率见表7，结果表明黑洞材料换作密度与模量更小的环氧树脂时，结构的带隙特性进一步向低频移动，进一步佐证了3.2 节中的结论。这是由于黑洞结构材料变化时，一方面材料本身密度与杨氏模量较小，使得结构的固有频率向低频移动；另一方面黑洞部分与基体的阻抗失配效应更明显，更容易形成弯曲波带隙。

对比图16与图8以及图14给出的位移传递函数曲线也可以看出，同样的频率区间内，黑洞材料越“软”，基体与黑洞阻抗失配效应越强，带隙特性越容易在低频出现，出现带隙的数量就越多。这为基于周期声学黑洞抑制低频振动提供一定借鉴。

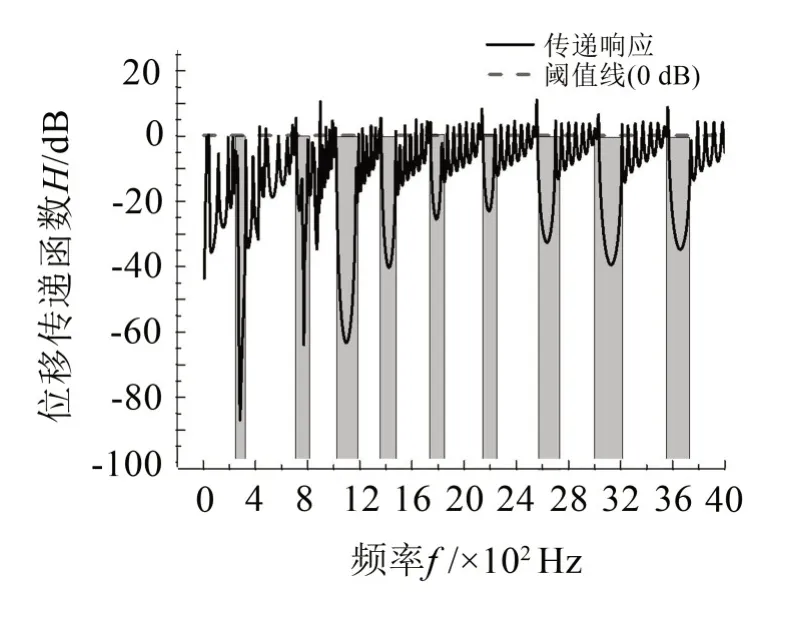
图16 环氧树脂黑洞梁位移传递函数

4 结 语

本文将声学黑洞与声子晶体相结合，采用有限元法研究了一种无限周期声学黑洞梁的能带结构与有限周期声学黑洞梁的弯曲波带隙与振动传递特性，并与恒定截面梁、单黑洞梁及周期楔形梁进行了对比，得到了如下结论：

(1)声学黑洞作为截面幂律变化的结构，将其周期构造成一维声子晶体，相较于单黑洞梁与周期楔形梁，能产生较好的弯曲波带隙特性。有限周期黑洞结构带隙特性与无限周期结构带隙特性类似，且除了禁带区间，在其附近的频带内由于声学黑洞效应，振动位移衰减特性也十分明显。这表明周期排列声学黑洞结构对于抑制结构弯曲波的有效性。

(2)将黑洞材料变换为密度与刚度较小的材料嵌入基体后，由于材料间的阻抗失配可以让声学黑洞结构在更低频范围内出现带隙特性，且相同频率区间内，带隙数量越多，抑制弯曲波传播的频段更宽，抑制振动传递的效果越好。这为周期性声学黑洞结构抑制低频振动提供新的研究方向。