汽轮机蒸汽力对动叶变形影响的数值计算分析

黄柳燕 范志飞 苟小平 莫一波

（东方电气集团东方汽轮机有限公司， 四川 德阳， 618000）

0 引言

动叶变形是汽轮机通流间隙设计时需考虑的重要因素。 汽轮机运行时， 蒸汽力将对动叶变形产生影响， 从而影响通流间隙。 因此， 本文从该角度出发， 计算分析蒸汽力对动叶变形的影响。

根据动叶型式的不同， 可以将动叶分为自由叶片和成圈叶片。 动叶结构的差异影响动叶刚度，因此变形必定不同。 工程上需定量计算出蒸汽力对单只动叶及成圈动叶的变形影响。

汽轮机运行时， 作用在叶片上的气流力可以分解为周向分力Pu和轴向分力Pa。 圆周向分力可以由级的轮周功率来确定[1]：

式中：Pu为周向气流力， N；Nu为级的轮周功率，kW；u为平均圆周速度， m/s；Z2为叶轮上动叶片数目；ε为部分进汽度。

轴向分力可由轴向分量气体动量变化和叶片前后的静压差确定， 由此得到对每个叶片的轴向作用力：

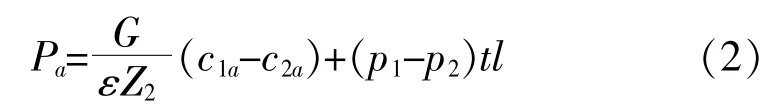
式中：Pa为轴向气流力， N；G为通过级的气体质量流量， kg/s；c1a、c2a为叶片进出口气流的轴向分速度， m/s；p1、p2为叶片前后气体静压力， N/m2；t为叶片节距， m；l为叶片高度， m。

从式（1～2）可知， 蒸汽力跟动叶只数、 叶高、平均圆周速度、 轮周功以及动叶前后压差有关。平均圆周速度会随着动叶级数增加而增加， 但是动叶只数的变化， 蒸汽力也会变化。

1 物理模型和计算方法

1.1 计算模型

为了对比分析， 本文选取某1 000 MW 汽轮机高压第1 级， 第8 级， 第17 级动叶进行数值模拟。 该高压通流进汽参数为12.66 MPa/630 ℃， 取危险工况对动叶进行结构设计， 动叶的几何模型及热力参数见表1。

表1 动叶的几何尺寸及热力参数

用PROE 建立动叶的三维模型， 并导入到ABAQUS 中进行前处理。 为减少网格造成的结果差异， 3 个模型的网格尺寸、 类型均相同。 网格尺寸为4 mm， 叶根处采用一阶六面体网格， 叶身处采用精度较高的二阶四面体网格[2]。 动叶网格模型见图1。

图1 某1 000 MW 汽轮机高压动叶网格模型

本文采用ABAQUS 软件进行有限元计算分析，计算各级动叶本身在离心力载荷及蒸汽力作用下的动叶变形， 并考虑成圈动叶与单只动叶在蒸汽力作用下位移变形差异。

1.2 边界条件和加载

模型1～3 均约束叶根工作面处3 个方向的平移边界。 该边界会使约束面处的应力较大， 但鉴于本计算主要探讨围带顶部的变形情况，且根据圣维南原理可知，其对围带处的影响微乎其微。

对各模型加载离心力及蒸汽力。 蒸汽力以集中力的形式加载于叶身中间截面若干节点处。 各模型蒸汽力的加载情况见表2。

表2 各模型蒸汽力加载数值表

2 计算结果及分析

模型1～3 的位移结果云图如图2 所示。

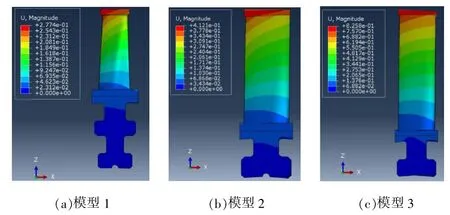
图2 模型的位移结果云图

对模型1～3 加载蒸汽力前后的位移进行对比分析， 结果如图3～5 所示。

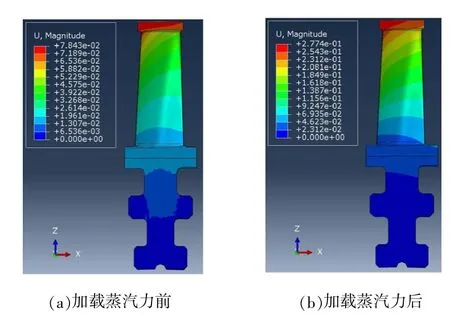
图3 模型1 的位移结果云图

图4 模型2 的位移结果云图

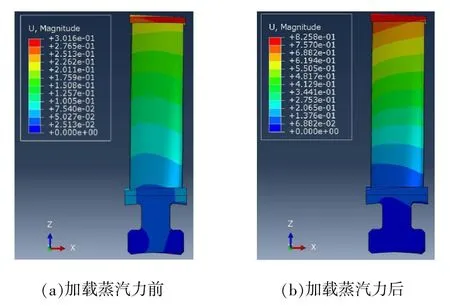
图5 模型3 的位移结果云图

为了更好地分析蒸汽力对变形的影响， 本次计算选取围带顶部的4 个节点对其进行定量分析，选取节点的位置如图6 所示。

图6 考察节点位置图

因考察节点在加载蒸汽力前后的变形差值，故本文对结果进行初步处理， 将加载蒸汽力后的节点位移值减去加载蒸汽力之前的节点位移值，即

式中：U'为加载蒸汽力后的节点位移值；U为加载蒸汽力之前的节点位移值。

模型1～3 加载蒸汽力前后的变形差值见表3。

表3 模型1～3 加载蒸汽力前后图示节点变形差值表

通过图表形式可更直观看出其变形规律， 故作出表3 的图形， 如图7 所示。

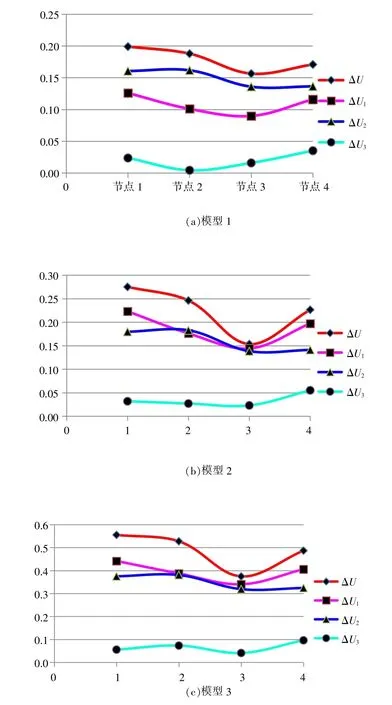
图7 模型1～3 加载蒸汽力前后节点变形差值

从表3 及图7 可知， 针对本计算分析中的3个模型， 蒸汽力对轴向变形影响的最大值为0.442 mm， 对周向变形影响的最大值为0.381 mm， 对径向变形影响的最大值为0.096 mm。

且从表3 及图8 可知， 模型1、 2、 3 的曲线相似， 即各模型节点加载蒸汽力前后变形规律相同， 且随着蒸汽力的增加， 变形差值增大， 故蒸汽力对模型3 的影响最大； 对任一模型而言， 节点1 处对蒸汽力最敏感， 变形差值最大； 相比较蒸汽力对轴向位移和周向位移的影响而言， 其对径向位移的影响几乎可以忽略不计， 即便在模型3处， 最大径向变形差值也只有0.096 mm， 这是由于蒸汽力的方向为轴向和周向， 故其对轴向位移及周向位移影响较大。

以上3 个模型的对比分析均是建立在单只叶片的基础上， 工程实践中， 成圈叶片较多， 因此，计算分析成圈叶片对蒸汽力弯应力的反响是非常必要的。 从以上的分析中可知， 模型3 由于蒸汽力大， 动叶高度大， 故其刚度略差， 对蒸汽力反应相对明显。 故本文对比分析模型3 的成圈叶片在加载蒸汽力前后的变形差异， 该模型即前文所提到的模型4。 成圈叶片在单只动叶模型基础上设置循环对称， 且为模拟工程实际情况， 在围带处设置了0.25 mm 的过盈量， 以满足接触应力的规范要求， 其余有限元前处理均相同。 接触面处接触应力情况云图如图8 所示。

图8 模型4 接触面处接触应力云图

成圈模型位移结果云图如图9 所示。

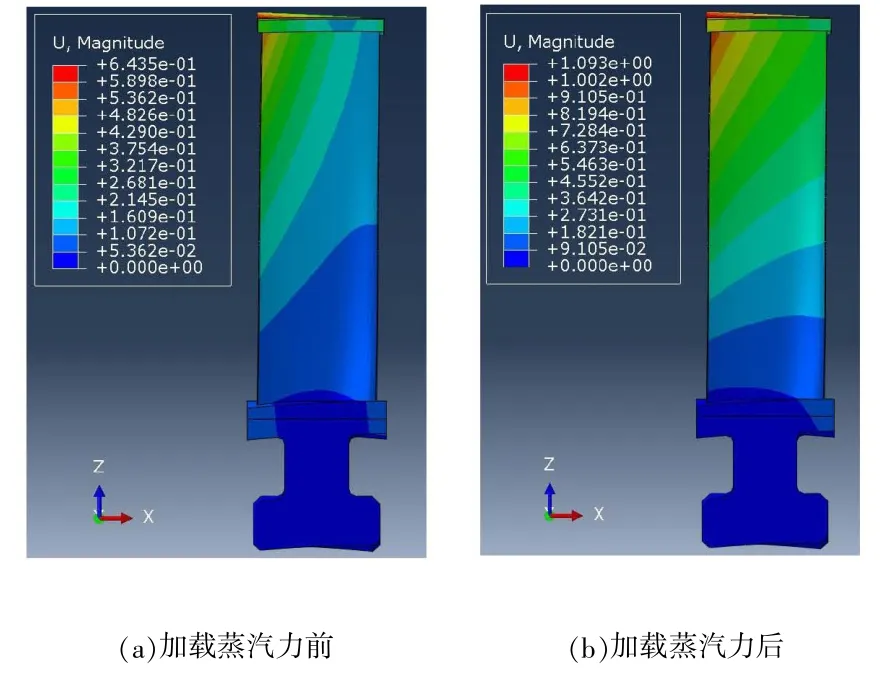
图9 模型4 位移变形结果云图

提取相关数据进行对比分析， 见表4。

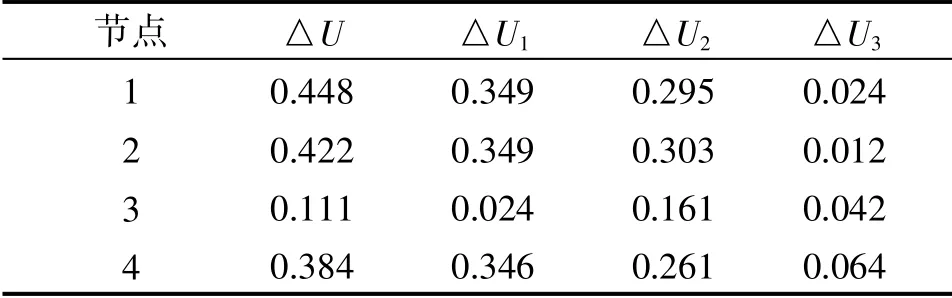
表4 模型4 加载蒸汽力前后图示节点变形差值表

因模型4 为成圈叶片， 故节点2、 3 的位置随着围带块的旋转而在几何空间位置与之前有所不同， 模型4 中各节点的位置如图10 所示。

图10 模型4 中各考察节点位置

对于该4 个节点是否与原节点匹配， 可以从位移计算结果（见图11）中看出， 尽管节点空间位置发生了变化， 但不影响其在有限元计算中的位移结果连续性。

图11 模型4 围带位移结果云图

对比模型3、 4 的各节点变形情况， 结果如图12 所示。

图12 模型3 与模型4 各节点变形差值对比图

从图12 可知， 成圈叶片在蒸汽力的作用下，轴向变形最大差值从单只叶片的0.442 mm 降低到0.349 mm， 径向变形最大差值从0.096 mm 降低到0.064 mm。 且相比较模型3 中各节点加载蒸汽力前后的变形差值， 模型4 中各节点在加载蒸汽力后的变形差值均出现明显减小趋势， 这与理论是相符的。 因为成圈叶片增加了叶片的刚度， 使得叶片的变形相对减小。

3 总结

本文计算分析了某1 000 MW 汽轮机不同级次的动叶模型在加载蒸汽力前后的位移差值， 并进一步计算分析了单只叶片与成圈叶片在加载蒸汽力前后的差值差异， 得出以下结论：

（1）蒸汽力对动叶的变形有一定影响， 不管是单只叶片还是成圈叶片， 且随着蒸汽力的增大，变形增大；

（2）成圈叶片与单只叶片相比， 由于增加了动叶的刚度， 故蒸汽力对其变形的影响相对减小，其中轴向变形最大差值从单只叶片的0.442 mm 降低到0.349 mm， 径向变形最大差值从0.096 mm 降低到0.064 mm。