基于同步挤压改进短时傅立叶变换的分频蚂蚁追踪在断裂识别中的应用

黄苇,周捷,高利君,王胜利,严海滔

(1.中国石油化工股份有限公司 西北油田分公司勘探开发研究院，新疆 乌鲁木齐 830011； 2.成都理工大学 地球物理学院，四川 成都 610059)

0 引言

近些年由于油气勘探力度不断增大，浅层构造油气藏几乎已完成开采；油气勘探工作者逐渐将浅层构造油气藏的目光转向深层油气藏。由于大地滤波、吸收衰减等因素使得地震波能量在向下传播过程中发生严重衰减，因此，对深层油气藏的探寻变得愈发艰难。油气从生成层转移至储集层时需要通道，所以，储层发育的裂缝扮演着不可或缺的角色；它将影响着储层的渗透性以及连通性，直接决定着油气的产量；因此，对于微小断层的刻画或者裂缝发育带检测已然成为油气储层预测中非常重要而又迫切的问题。

裂缝、断层检测方法经过多年的发展研究，自1995年Bahorich M[1]提出地震相干数据方法后，Amoco公司将地震相干技术应用于地震资料断裂系统检测，取得了很好的效果。1998年Marfurt[2-4]基于相似性算法，提出了比第一代相干算法更能描绘断层的第二代相干体算法；1999年Gersztenkorn等基于本征结构以及协方差矩阵，提出了第三代相干算法，从而求取多道地震数据彼此的相关性；第三代相干算法相比第一代和第二代相干算法，其提高了地震数据的纵向、横向分辨率，且将该算法推广到三维地震数据体中，不需要层位约束，但是对于许多微小断裂以及次生裂缝无法进行精细的刻画。王西文等[5]把小波变换和相干算法相融合，该算法比传统相干算法有更高的分辨率，但刻画小裂缝的效果依旧不理想。1999年Dorigo等[6]提出了基于蚁群算法的蚂蚁追踪技术，该算法模仿蚂蚁觅食遇到障碍所释放的信息素来追踪断层以及裂缝。目前，蚂蚁追踪技术是公认的一种能有效刻画断层以及裂缝的技术。但在实际应用中该技术仍存在些许精度上的缺陷，如许多高陡构造，由大断层而衍生出来的微小裂缝、断层等，蚂蚁追踪技术将无法准确地雕刻。

Partyka等[7]于1999年提出了将全频带的地震数据体分解为各个频率的单频数据体的频谱分解技术，以此反映出全频带地震数据中无法凸显出的地质信息。2009年Zeng等[8]利用频谱分解技术得到不同频率的地震数据体，结果显示单频地震数据体比全频带数据体对地下异常体的区域范围能有更清晰的勾勒，并且能刻画更多细节。以上学者都为频率域的资料解释做了极大的贡献。

Daubechies等[9]将小波变换后的频谱值在时频域内进行挤压以及重新排列，提出了将时频聚焦能力提高的同步挤压算法。2017年Yu G等[10]将短时傅立叶变换窗函数延展，使其结果比短时傅立叶变换的分辨率更高，但是，它仍会因为海森堡原理的制约以及交叉项干扰使时频分析精度受到很大限制。

因此，根据同步挤压算法原理，通过对改进短时傅立叶变换后的时频谱挤压重排来发展同步挤压改进短时傅立叶变换，理论信号表明，该方法具有比传统时频分析方法更高的时频分辨率。结合之前学者的研究成果[11-19]，本文利用同步挤压改进短时傅立叶变换在时频聚焦上的优势，对某工区的三维地震数据体进行频谱分解从而获取各个频率的单频数据体；再应用蚂蚁追踪技术对单频数据体进行计算。其结果表示该方法可以对微小裂缝进行细腻的勾勒，并证明了其在实际应用中的准确性及实用性。

1 方法原理

傅立叶变换可以算是时频分析领域的鼻祖，但其无法对非平稳信号进行很好地刻画；而现实中的信号几乎为非平稳信号，尤其是地震信号，傅立叶变换早已无法达到人们对精度的要求。短时傅立叶变换通过增加窗函数去截断非平稳信号，并将整个非平稳信号分割成数个小段，这时便可把窗函数里的每段信号看作平稳信号，再对每个小段信号分别做傅立叶变换便得到了二维时频谱图。

假设信号x(t)∈L2(R)，则信号的数学表达式为：

x(t)=Asin(ct+φ) ，

(1)

式中：A为幅值,cm;c为角频率,Hz;t为时间，s；φ为初始相位角；L2(R)是实数域中的平方可积函数空间；x(t)表示信号。

信号x(t)的短时傅立叶变换(Sstft)表达式为：

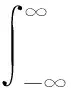
式中：f为频率,Hz；τ为时窗长度，常数；i表示虚数；g(t-τ)为随τ的变化在时间轴上运动的窗函数。但短时傅立叶变换的窗函数固定且唯一，这意味着信号截断的位置以及时窗长度对计算结果的影响特别大。

将式(2)离散化得到离散傅立叶变换(Sstftx)表达式为：

(3)

1.1 改进短时傅立叶变换

由于短时傅立叶变换时窗无法改变这一缺点限制了该方法提高时频聚焦性，想要克服这一缺陷必须要对时窗函数进行改进。由式(2)，分别求出信号和窗函数的复共轭，则可以得到：

(4)

(5)

令t-r=r，则有

(6)

(7)

原始Sstft的表达式为式(2)，则改进短时傅立叶变换(Gstft)的表达式为：

1.2 同步挤压改进短时傅立叶变换

根据改进短时傅立叶变换的公式，首先，计算Gstft对时间t导数为：

(9)

则可以得到信号的瞬时频率表达式：

(10)

根据式(10)得到的瞬时频率，可以得到同步挤压改进短时傅立叶变换(Sgstft)值的表达式为：

式中：η为同步挤压变换后的时频谱频率值，Hz。

同步挤压改进短时傅立叶变换则是对短时傅立叶变换改进后的时频谱值在时频域内进行挤压以及重排并将其置于瞬时频率处，进而提高信号的时频聚焦性。

1.3 蚂蚁追踪技术

蚂蚁追踪技术是在蚁群算法的基础上发展起来的，模仿蚂蚁觅食所释放的信息素指导其他蚂蚁进行追踪，对断裂信息有着非常强的识别能力。但是对于许多伴生褶皱以及次生裂缝，基于原始数据进行的蚂蚁追踪无法进行有效的刻画。为避免破坏实际地震资料的纵横向分辨率，所以实际地震资料处理对时频分辨率的要求较高。传统时频分析方法，如短时傅立叶变换，S变换，WVD等，受自身窗函数的制约，时频分辨率无法达到最佳，甚至还会产生许多虚假信息；尤其是WVD，由于WVD方法在计算时会产生意想不到的交叉项，导致其结果存在很大的误差。而同步挤压算法利用压制海森堡不确定性以及交叉项影响上的优势使得结果具有很高的分辨率，这一点在实际应用中被很好地验证。

基于此，在三维地震断裂解释中，本文将蚂蚁追踪技术与同步挤压改进短时傅立叶变换在时频分析中的优势相结合，利用不同频率信息对地震数据断裂系统进行雕刻，主要操作步骤为(图1)：

1)应用同步挤压改进短时傅立叶变换对三维地震数据体做频谱分解，分别获得低频、中频、高频的数据体。

2)对单频数据体开展边缘检测、边缘增强等工作，如：提取单频数据体的方差体、混沌体、相干体、曲率属性等；再对这些属性体平滑增强，从而使数据体中存在的不连续处暴露出来。

3)再将蚂蚁追踪技术应用于上述属性体，得到单频的蚂蚁属性体。

图1 基于同步挤压改进短时傅立叶变换分频蚂蚁追踪流程框架Fig.1 Improved ant tracing process framework of short-time Fourier transform based on synchronous extrusion

2 模型数据测试

为了验证该方法的时频分辨能力以及抗噪性，合成由x1、x2、x3、x4叠加的线性调频信号：

(12)

应用短时傅立叶变换、改进短时傅立叶变换、同步挤压改进短时傅立叶变换分别对信号x进行时频变换，对比分析其时频聚焦能力。

对比图2中三幅时频谱图可以得出：改进短时傅立叶变换的时频分辨率较短时傅立叶变换得到了一定的提升，但海森堡不确定性以及交叉项干扰仍然是阻碍分辨率提高的重要因素；同步挤压改进短时傅立叶变换的时频谱图中，其结果不仅能量汇聚度强、时频分辨率高，并且解决了短时傅立叶变换时窗不变的缺陷。在短时傅立叶变换以及改进短时傅立叶变换的基础上，计算得到的同步挤压改进短时傅立叶变换值是对改进短时傅立叶变换的再处理过程，由于改进短时傅立叶变换分辨率的局限性，使得信号在每一个时间点所对应的瞬时频率不止一个，因此产生了虚假带宽的问题。同步挤压改进短时傅立叶变换在改进短时傅立叶变换的基础上，对虚假带宽进行挤压，重新排列于信号的瞬时频率附近，使得信号的时频分辨率得到了极大的提升。

a—原始合成信号;b—短时傅立叶变换的时频谱;c—改进短时傅立叶变换的时频谱;d—同步挤压改进短时傅立叶变换的时频谱a—original synthesized signal;b—time frequency spectrum of short time Fourier transform;c—improved time frequency spectrum of short time Fourier transform;d—synchronous to improve time frequency spectrum of short time Fourier transform图2 合成信号及利用不同分析方法得到的时频谱Fig.2 Synthesized signal and time spectrum obtained by different analysis methods

对信号x进行随机加噪，从而验证本文方法的抗噪性(图3)。通过观察时频谱信息可以知道，在对信号添加随机噪声后，短时傅立叶变换、改进短时傅立叶变换、同步挤压改进短时傅立叶变换的时频能量都受到噪声干扰，但是同步挤压改进短时傅立叶变换的有效信息保留得较好，整个时频谱图依旧比较干净，受噪声影响很小。因此，同步挤压改进短时傅立叶变换算法具有一定的抗噪能力。

传统时频分析方法是对每一道地震数据进行处理，因此改进短时傅立叶变换在纵向分辨率上得到了很大的提升，然而断裂尺度等信息是和横向分辨率相关的。同步挤压改进短时傅立叶变换在提升信号纵向分辨率的同时，开展了多道间的挤压，即对多道地震记录同时做挤压以便兼顾地震数据的横向分辨率。

通过对比分析图4原始地震剖面及单频剖面可以发现，对单道地震记录循环做同步挤压短时傅立叶变换所得到的单频剖面，其纵向分辨率相较于改进短时傅立叶变换得到了很大的提升，但是其横向分辨率却存在较大的弊端；因此开展了多道间的同步挤压短时傅立叶变换，对比单道的同步挤压短时傅立叶变换，多道的同步挤压短时傅立叶变换无论其纵向分辨率还是横向分辨率都得到了极大的提升。

本文所使用的数据属于某工区三维地震数据体。频谱分解技术首先需要确定频率值的大小，频率值直接决定着单频剖面中的有效信息能否被准确的描绘出来；因此，频率值的选取在整个流程中占据十分重要的位置。本文首先对实际地震数据的井旁道做时频变换处理，通过确定该地震资料的优势频带范围，从而确定频率值的大小，以突出所需要的地震数据有效信息。

首先对原始地震资料分别使用短时傅立叶变换以及同步挤压改进短时傅立叶变换提取井旁道做频谱分析得到图5频谱。分析图5中同步挤压改进短时傅立叶变换时频能量分布可知，该地震数据体的优势频带范围位于25～60 Hz。因此，选取25、55 Hz作为单频数据体的频率值。

a—原始加噪信号;b—短时傅立叶变换的时频谱;c—改进短时傅立叶变换的时频谱;d—同步挤压改进短时傅立叶变换的时频谱a—original noise signal;b—time frequency spectrum of short time Fourier transform;c—improved time frequency spectrum of short time Fourier transform;d—synchronous to improve time frequency spectrum of short time Fourier transform图3 加噪信号及利用不同分析方法得到的时频谱Fig.3 Noise-added signal and time spectrum obtained by different analysis methods

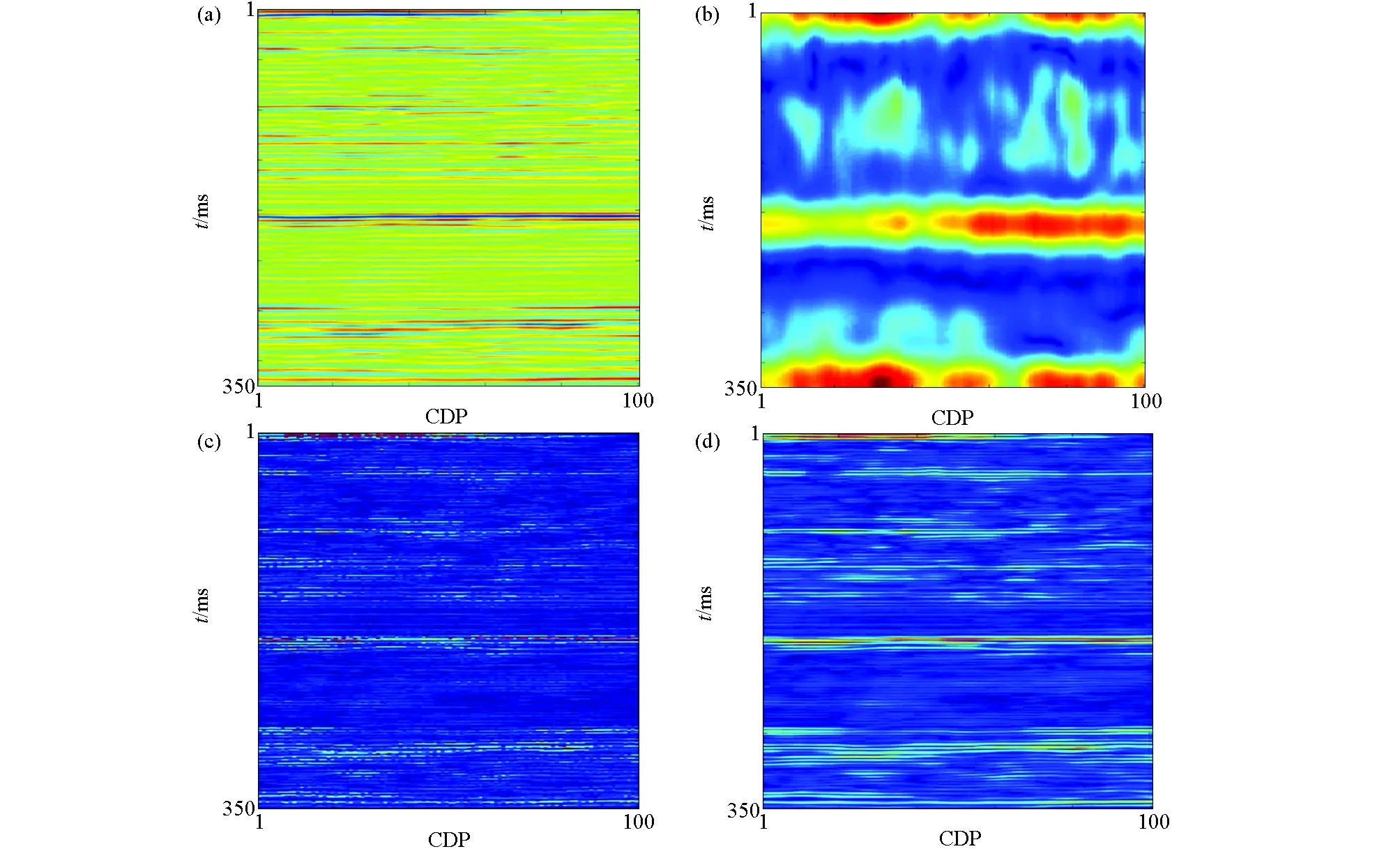
a—原始地震记录;b—改进短时傅立叶变换单频剖面;c—单道循环挤压改进短时傅立叶变换单频频谱;d—多道循环同步挤压改进短时傅立叶变换单频剖面a—original seismic signal;b—improved short time Fourier transform single frequency profile;c—single channel cycle squeeze to improve short time Fourier transform single frequency profile;d—multi channel cycle squeeze to improve short time Fourier transform single frequency profile图4 原始地震记录及单频剖面Fig.4 Original seismic record and single frequency profile

a—井旁单道地震记录;b—短时傅立叶变换得到的时频谱;c—同步挤压改进短时傅立叶变换得到的时频谱a—single channel seismic record near the well;b—time frequency obtained by short time Fourier transform;c—synchronous squeezing to improve the time spectrum obtained by short time Fourier transform图5 井旁地震道及利用不同分析方法得到的时频谱Fig.5 Seismic trajectory by the well and the time spectrum obtained by different analysis methods

3 应用实例

基于以上理论基础以及模型分析可以知道，同步挤压短时傅立叶变换相较于传统的时频分析算法具有很高的时频聚焦能力，可以压制信号时频变换过程中产生的虚假带宽问题，将信号的真实瞬时频率凸显出来。因此应用同步挤压短时傅立叶变换所得到的单频数据体可以刻画出传统时频分析算法所无法描绘的断裂系统信息。基于上述知识，本文将同步挤压改进短时傅立叶变换应用于实际地震资料，分析得出同步挤压改进短时傅立叶变换在处理实际地震数据时的准确性。分别对三维地震数据体提取25、55 Hz的单频数据体，再对单频数据体做边缘增强，计算得到单频蚂蚁体。

图6为原始振幅沿层切片，图7为全频带沿层蚂蚁体切片，图8、图9分别为25、55 Hz单频蚂蚁体沿层切片。

在单频蚂蚁体中，许多微小断裂信息被很好地雕刻出来，25 Hz单频蚂蚁体与全频带蚂蚁体都对于大断裂信息进行了详细的描绘，而55 Hz相对高频的蚂蚁体对许多微小断裂信息做了很清晰的刻画。

全频带蚂蚁体可以对大断层、中断层进行了非常清晰地描绘；单频蚂蚁体中，随着频率升高，剖面中一些细微的断裂信息被凸显出来；但是随着频率的增加，噪声信息也会被放大，因此，在高频剖面中会出现一些采集脚印等干扰信息；但是单频蚂蚁体技术能够识别出全频带蚂蚁体无法刻画的小断裂，具有很高的实用价值。

结合上述基于同步挤压短时傅立叶变换所得到的中、高频蚂蚁体对微小断裂信息有着较强的刻画能力，低频蚂蚁体可以对大、中断层进行详细雕刻。

图6 振幅沿层切片Fig.6 Amplitude slice along the layer

图7 全频带沿层蚂蚁体切片Fig.7 Full-band ant slice along the layer

图8 25 Hz沿层蚂蚁体切片Fig.8 25 Hz ant slice along the layer

图9 55 Hz沿层蚂蚁体切片Fig.9 55 Hz ant slice along the layer

4 结论及建议

进行分频属性检测，时频分析是核心，传统的时频分析方法在纵横分辨率上已无法达到人们对精度的要求，尤其是纵向分辨率；而同步挤压变换算法可以很好地提高地震数据的纵向分辨率；因此，在同步挤压变换算法上进行分频属性提取，会达到比传统时频分析算法更好的效果。

本文应用同步挤压改进短时傅立叶变换对地震数据进行频谱分解，有效地压制噪声的影响，对后续的蚂蚁体计算提供了高信噪比数据体；并且高频蚂蚁数据体可以刻画出全频带蚂蚁体无法刻画的微小断裂以及伴生褶皱等信息；尤其在裂缝发育带，该方法可以较为准确地雕刻其分布区域以及特征；数据体融合重构技术能够汇集低频、中频、高频等裂缝信息，对断层可以更进一步的清晰描绘。基于同步挤压改进短时傅立叶变换的分频蚂蚁追踪方法能够精确地描绘出区域断裂系统信息，为后续储层产量预测以及井位的确定提供现实依据。后期为了得到更加精细的断裂特征，可以参照RGB技术的思想，将低频、中频、高频蚂蚁数据体进行融合重构，得到一个新的蚂蚁数据体；该蚂蚁数据体将同时具备低频的信息，也将具备中频、高频的裂缝信息；它可以很清晰地描绘出断层的发育走向、微小裂缝以及伴生褶皱等综合信息。