隧道勘探AMT数据二维非线性共轭梯度反演的关键参数探讨
赵广学,阮帅,吴肃元
(1.恒达新创(北京)地球物理技术有限责任公司,北京 100020; 2.中国地质科学院,北京 100037)
0 引言
在铁路隧道施工前期,利用音频大地电磁测深(以下简称AMT)对施工线进行断层破碎带、溶洞等地质灾害隐患评估时,勘探数据的确定性和分辨率都非常重要,但二者往往不可兼得,提升反演分辨率意味着增加假异常的出现几率,造成过度风险评估,反之则会增加施工风险,造成安全事故。因此,对铁路隧道AMT勘探数据的反演进行更深入的研究极其重要。
1 复杂地电模型及二维非线性共轭梯度反演
在石油勘探领域,研究多在地质条件接近一维的情况下进行,AMT一维反演纵向分辨率较高,往往通过浅层电阻率调查对观测数据进行静态位移校正,然后再进行一维反演直接解释,能得到不错的地层分辨率。但这种反演方案只适应于沉积岩地层,在复杂地形地质条件下,静位移校正并无简单规律可循,盲目地使用一维反演方案会出现电阻率失真和中、浅层假异常的问题。隧道勘探的数据反演应该使用二维算法,避免对输入数据的静态效应校正,除非因观测电极距测量误差出现明显的曲线平移现象。
目前,主流的AMT二维反演算法是Rodi和Mackie(2001)改进的非线性共轭梯度法(以下简称NLCG),它避免了直接求解雅克比矩阵,一次反演迭代只需3次正演,从而大大节省了计算量,具有迭代稳定,内存需求小的优点,非常适应二、三维MT/AMT数据反演。其目标函数定义为[1]:
Ψ(m)=[d-F(m)]TV-1[d-F(m)]+
λmTLTLm,
(1)
式中:m为反演模型;F(m)为模型的二维正演响应;d为观测数据;λ为正则化因子,控制模型修正沿着光滑方向还是数据最佳拟合方向;V是正定矩阵,为误差向量的方差;L为拉尔朗日算子矩阵。
若使用线性共轭梯度法求解式(1)的极小值,对于每次迭代,需进行以下模型修正:
k=0,1,…,k-1。
式中:ml为第l次迭代的模型,pl,k控制了第l次迭代中的模型修正方向,αl,k为修正步长因子。

自2001年以来,这一反演方案成为大地电磁(MT)与AMT数据反演研究和应用最多的方法[3]。不过,在实际应用中,若改变不同的反演参数(如初始模型、正则化因子),同一组数据的反演结果存在较大的差别,不同的参数控制了模型的修正方向,侧重点可以是放在反演结果的平滑度上,也可以是观测数据的拟合度。因此对于具体的地质任务,往往需要通过多种组合实验的方法获取最佳选择方案。
基于以上事实,为适应铁路隧道AMT勘探的解释需求,按照西南某铁路隧道线的地形、地质情况建立地电断面模型(图1)。该地电模型断面背景为类K型地电断面,背景地层电阻率自浅至深分别为20、100、500、800 Ω·m和100 Ω·m;在距离600~800 m、1 200~1 600 m处各存在一个低阻断层破碎带,电阻率10 Ω·m;距离2 000~2 200 m处存在一块电阻率为1 000 Ω·m的高阻空腔;分别在200~400 m、1 000~2 000 m、2 000~2 200 m的地形起伏处设置电阻率为500、500、100 Ω·m的浅层不均匀体以模拟静态效应。

图1 典型地电断面模型的正演网格Fig.1 Typical forward grid of geological model
对此模型的合成AMT数据(频带10 000~10 Hz)进行不同参数组合的二维NLCG反演[4],以分析参数选取对反演结果的影响,从而建立铁路隧道勘探二维NLCG反演的参数选取准则,适应地质解释需要。
2 反演网格的影响
图1的模型高程起伏剧烈,海拔最高的Q测点和最低的E测点之间高程差接近180 m,实际勘探中还有更剧烈的高程变化。只有精细的网格剖分才能准确模拟静态效应以拟合实测数据,但过密的反演网格会增加反演问题的病态,成倍增加计算时间。因此讨论反演网格的疏密对结果的影响非常必要。
选择2种网格进行对比研究。第一种是让测点位于网格中心、横向不做加密、纵向以1.2倍因子增长的粗糙网格(简称粗糙网格),本文设置的网格为64×16;另一种反演网格与合成数据的正演网格一致(简称精细网格),文中设置的网格为64×64。为不失一般性,本文使用统一的迭代次数,在相同的迭代次数下进行对比。初始模型为100 Ω·m均匀空间,最大迭代次数100次,正则化因子取3,合成数据的各种反演组合的结果如图2~图7所示,反演收敛RMS方差如表1所示。
比较图2和图3可知,只选用TE模式数据进行NLCG反演时,网格的粗糙度对反演结果的影响不是太大,两个反演结果的断层破碎带和高阻空腔的位置基本一致,地层电阻率也基本正确[4]。
和TE模式数据反演不同,参照图4和图5可见,若只选取TM模式数据进行反演,粗糙网格的反演结果对破碎带的分辨能力下降,二者的电阻率值有较大差别。
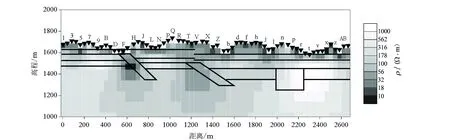
图2 粗糙网格TE模式反演结果(图例同图1)Fig.2 Rough mesh TE mode inversion results (The legend is the same as Figure 1)

图3 精细网格TE模式反演结果(图例同图1)Fig.3 Fine mesh TE mode inversion results (The legend is the same as Figure 1)

图4 粗糙网格TM模式反演结果(图例同图1)Fig.4 Rough mesh TM mode inversion results (The legend is the same as Figure 1)

表1 不同网格、不同模式的反演RMS误差
若同时对TE和TM模式的数据进行反演(参考图6和图7),二者的横向分辨率差不多,不同之处在于粗糙网格的剖面整体电阻率相对较高,对于铁路勘探而言这不是重要问题,对高阻空腔的反映能力还是精细网格更好。
若考虑反演的RMS误差,参考表1,所有粗糙网格的最终RMS误差都在2以上,而精细网格的RMS误差都小于1。精细网格不但有利于模拟静态位移、实现更准确的异常分辨,更有利于达到更小的RMS误差。

图5 精细网格TM模式反演结果(图例同图1)Fig.5 Fine mesh TM mode inversion results (The legend is the same as Figure 1)

图6 粗糙网格TE+TM模式联合反演结果(图例同图1)Fig.6 Rough mesh TE+TM mode inversion results (The legend is the same as Figure 1)

图7 精细网格TE+TM模式联合反演结果(图例同图1)Fig.7 Fine mesh TM+TE mode inversion results (The legend is the same as Figure 1)
综上所述,实际资料反演中,若只使用TE模式反演,网格可相对粗糙;若TM模式数据参与反演,则要求地表网格相对精细,以尽量精确地模拟地形变化。图6和图7是最佳的铁路隧道勘探反演方案,即使用相对精细网格的TE+TM模式联合反演。
3 不同频带的反演实验
由于AMT的高频部分主要场源为高空雷电,一般在晴朗的上午,即使工区干扰较小,也会在5 000~1 000 Hz频带出现较差的信噪比,造成观测曲线脱节。这个频带也被称为“死带(death band)”。由于“死带”影响,野外数据高于1 000 Hz的功率谱取舍很难,有些学者使用插值计算出“死带”数据,不过这并非真实的二维响应。
为评估“死带”对深部异常体的二维NLCG反演影响,对图1的合成数据使用1 000~10 Hz的中、低频数据进行精细网格反演,其结果如图8~10所示,其他控制参数和本文第2节一致,反演的最终RMS误差如表2所示。
比较图3和图8可见,对于TE模式反演,舍弃高频数据(10 000~1 000 Hz)之后,反演结果基本相同,不同的是图3由于有更多的高频数据参与反演,对1 200~1 400 m处的低阻破碎带分辨更好。
比较图5和图9可见,TM模式数据的二维NLCG反演对高频数据更依赖,两个断层破碎带的形状和深度都发生了较大的变化,这是因为TM数据的高频部分更易受到地形和地表不均匀影响,若不拟合高频部分则模型等效性更强。
对比图7和图10,若使用TE和TM数据联合反演,无论是否保留高频数据,深部模型的结果差别不大,对3个横向异常都有明显反映,且地层电阻率无明显差别。
从反演的RMS误差看,舍弃高频部分更有利于数据拟合,采取1 000~10 Hz的数据进行反演的最终RMS误差均小于0.5,因此若实测资料有比较严重的“死带”现象,只要使用TE+TM联合模式的精细网格反演,不妨将10 000~1 000 Hz的高频数据舍去。该对比由于频点数不一样,频点数少的拟合更容易,误差会更小,因此这个对比主要是对比反演结果的精细度。综上所述,实际资料的二维NLCG反演若单独使用TM数据,最好尽可能多地使用高频数据,以对静态位移现象进行最佳拟合,若反演输入数据是TE模式或TE+TM模式联合,可以考虑只使用1 000 Hz以下的数据进行反演。

表2 不同频带的反演RMS误差

图8 1 000~10 Hz 精细网格TE模式反演结果(图例同图1)Fig.8 1 000~10 Hz Fine mesh TE mode inversion results(The legend is the same as Figure 1)

图9 1 000~10 Hz 精细网格TM模式反演结果(图例同图1)Fig.9 1 000~10 Hz Fine mesh TM mode inversion results(The legend is the same as Figure 1)

图10 1 000~10 Hz 精细网格TE+TM模式联合反演结果(图例同图1)Fig.10 1 000~10 Hz Fine mesh TE+TM mode inversion results (The legend is the same as Figure 1)
4 不同正则化因子的反演实验
正则化因子实际上可视为一个加权系数,将数据拟合的目标函数和模型约束(粗糙度)目标函数联合起来,构成总目标函数[5]。在NLCG二维反演程序中,该值是一个经验常数,它既能让模型的修正在一定程度上拟合数据,挖掘数据的分辨率,又要求模型具有较好光滑度,以减少冗余构造。一般来说,正则化因子越大,模型越光滑,实际资料的最佳正则化因子往往采用实验的方式获得,文中分别选用0.3、3、30、300的正则化因子对1 000~10 Hz的合成数据进行TE+TM模式联合反演,其他反演参数同前,反演结果如图11~14所示,最终RMS误差见表3。

表3 不同正则化因子的反演RMS误差
由反演结果(图11~13)可见,在其他参数不变的情况下,随着正则化因子的增大,模型的分辨率越来越差,接近30~300的正则化因子的二维NLCG反演结果基本对深部断层破碎带和高阻空腔完全没有反映。
从表3可知,随着正则化因子的增大,为了让模型修正向更光滑的方向,牺牲了数据的拟合能力,当正则化因子达到300时,最终RMS误差达到 3.46。因此,对于本文讨论的铁路隧道的AMT数据二维NLCG反演应使用较小的正则化因子,一般可以在0.1~10之间进行反演实验,选取一个地层清晰、RMS误差又不太大的即可。

图11 1 000~10 Hz 精细网格TE+TM模式反演结果(正则化因子0.3)Fig.11 1 000~10 Hz Fine mesh TE+TM mode inversion results (smooth factor 0.3)

图12 1 000~10 Hz 精细网格TE+TM模式反演结果(正则化因子3)Fig.12 1 000~10 Hz Fine mesh TE+TM mode inversion results (smooth factor 3)

图13 1 000~10 Hz 精细网格TE+TM模式反演结果(正则化因子30)Fig.13 1 000~10 Hz Fine mesh TE+TM mode inversion results (smooth factor 30)
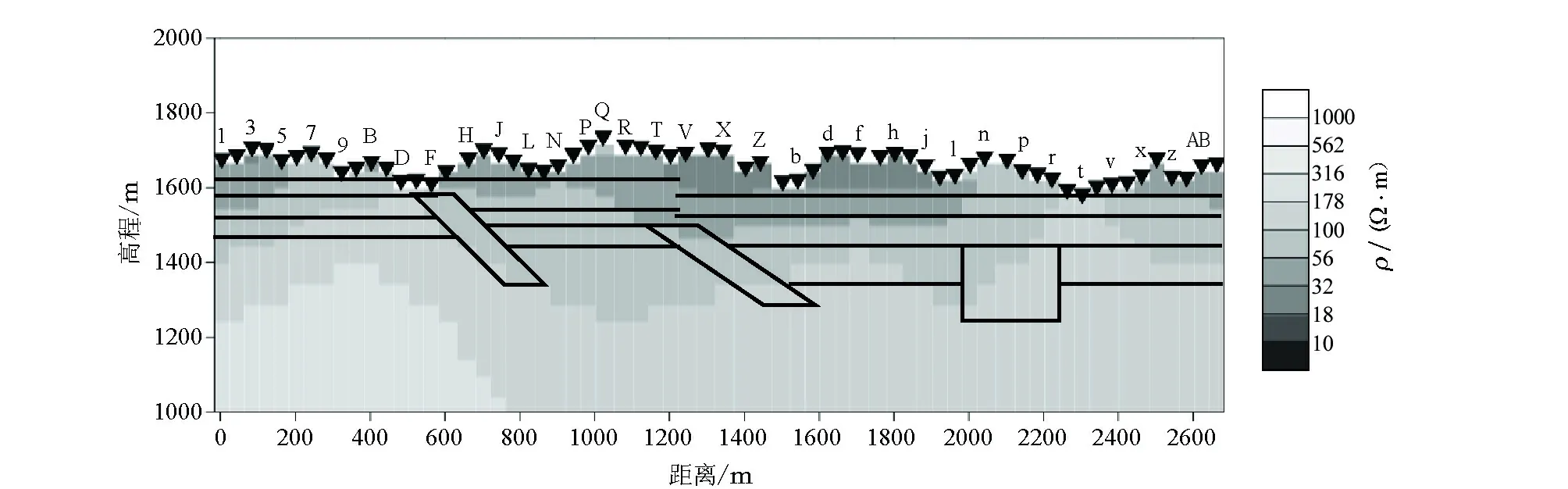
图14 1 000~10 Hz 精细网格TE+TM模式反演结果(正则化因子300)Fig.14 1 000~10 Hz Fine mesh TE+TM mode inversion results (smooth factor 300)
5 不同初始模型的反演实验
二维反演的初始模型会对最终结果产生影响,很多学者认为应该使用一维反演结果作为二维反演的初始模型[6]。但这一观点必须考虑二维NLCG算法的特点,若初始模型太粗糙(比如静态效应严重、或实测曲线不够圆滑的一维反演结果),则很有可能导致误差不收敛。
二维NLCG的初始模型最好比较光滑,可以考虑使用较大正则化因子的二维反演结果,但使用均匀半空间更有利于模型研究。选取10、100、500、1 000 Ω·m 4种均匀半空间作为初始模型,采用1 000~10 Hz的TE+TM联合数据,正则化因子取0.3,其他控制参数同前,反演结果如图15~18所示,最终RMS结果如表4所示。
由反演结果可知,所有模型的反演结果对于1 200~1 400 m处的断层破碎带基本正确,这证明二维NLCG反演对初始模型的依赖性相对较弱。不过,当初始模型增加到500 Ω·m后,600~800 m处的断层破碎带已经出现了错误的倾向,当初始模型变为1 000 Ω·m时,倾向错误更明显,而且反演结果的整体电阻率变得过大[7]。

图15 1 000~10 Hz 精细网格TE+TM模式反演结果(初始模型10 Ω·m)Fig.15 1 000~10 Hz Fine mesh TE+TM mode inversion results (initial model 10 Ω·m)

图16 1 000~10 Hz 精细网格TE+TM模式反演结果(初始模型100 Ω·m)Fig.16 1 000~10 Hz Fine mesh TE+TM mode inversion results (initial model 100 Ω·m)

图17 1 000~10 Hz 精细网格TE+TM模式反演结果(初始模型500 Ω·m)Fig.17 1 000~10 Hz Fine mesh TE+TM mode inversion results (initial model 500 Ω·m)

图18 1 000~10 Hz 精细网格TE+TM模式反演结果(初始模型1 000 Ω·m)Fig.18 1 000~10 Hz Fine mesh TE+TM mode inversion results (initial model 1 000 Ω·m)

表4 不同初始模型的反演RMS误差
参考表4给出的反演RMS误差可知,当初始模型的电阻率取得和中浅部地层电阻率接近时,RMS误差最小。因此,实际资料反演最好首先尝试选取和中、浅层电阻率较接近的初始模型,这一电阻率可用较大的正则化因子进行二维反演得到。
6 结论
进行了不同参数组合的典型铁路隧道AMT勘探的模型非线性共轭梯度反演试验,以确定实际资料反演的最佳参数选取方式。结论如下:
1) TM模式数据的反演对网格剖分要求更高。实际资料若只使用TE模式反演,可使用粗糙网格,但模型分析的结果建议铁路隧道勘探的AMT数据最好使用TE+TM模式联合反演,反演网格的浅层应尽量精细以精确模拟地形。
2) 类似的,TM模式对于参与反演的模型频带更敏感,实际数据若高频带较差需要舍去1 000 Hz以上的数据时,最好使用TE模式或TE+TM模式的联合反演。
3) 铁路隧道勘探结果需要相对精细的横向变化,所以二维NLCG反演不能片面追求模型光滑,在误差收敛、结果不影响背景地层的情况下,应尽量使用较小的正则化因子。
4) 二维NLCG反演的初始模型一般是均匀半空间,其电阻率值最好和中、浅层电阻率接近,若初始模型选择不合适,在TE+TM模式联合反演时可能会导致在深部断层倾向不明确的结果。有条件的情况下,可以参考较大正则化因子的二维NLCG反演结果来确定中、浅部的电阻率以正确选择初始模型。
必须提出,文中所有结论是基于特定模型得到的,对于更复杂的模型或者类A形、H型或Q型的地电断面,可能局部结论和本文不同,这些断面有待更多学者展开更多的细致研究,以提供更多铁路勘探AMT数据二维NLCG反演参数选取参考。

