基于模拟退火算法的阵列声波测井组分波慢度提取

周昊仪，莫修文，王丽丽，许宝寅

(1.中国地质调查局 广州海洋地质调查局 ，广东 广州 510075;2.吉林大学 地球探测科学与技术学院 ，吉林 长春 130026;3.中国石油天然气股份有限公司 吉林油田分公司 地球物理研究院 ，吉林 松原 138000)

0 引言

阵列声波测井起源于20世纪80年代。与常规声波测井相比，它可以利用多道重复信息弥补由于井径变化引起的误差。纵波信息以及其他组分波如横波、斯通利波等信息皆包含在内。对不同的组分波进行识别并准确提取其慢度是阵列声波测井数据处理的重要环节，也是进行岩石弹性参数计算[1]、地层各向异性分析[2]以及渗透率计算等的基础。因此，寻求高精度的提取方法是阵列声波测井解释的一项重要工作，关系到计算的岩性、孔隙度、渗透率以及饱和度等信息是否准确，能否为油气勘探和开发提供合理依据。

国内外学者对阵列声波测井组分波提取方法已进行了大量研究。Kimball等[3]提出慢度—时间相关(STC)法，它是一种时域的相关对比方法，优点是原理简单，计算速度快，缺点是时窗的选取会影响计算结果。Ingram等[4]提出直接相位法，它是STC法的频域表现形式，其优点是计算精度较高，缺点是计算速度较慢，且信噪比低时获得的结果较差。Hsu和Baggeroer[5]提出了最大似然法，其优点是计算精度较高，缺点是信号弱时结果不理想。乔文孝[6]提出时域及频域插值法，在一定程度上提高了声波时差的计算精度。章成广等[7]提出基于Prony理论的频谱法，当各组分波在时域上分离不明显时，其结果优于STC法，但是当地层较复杂时，其结果不稳定。陈强、张超谟[8]提出长短时窗能量比法，其优点是计算速度快，缺点是结果容易受多种因素影响，精度欠佳。宋延杰等[9]提出了慢度—时间相关法与遗传算法结合的阵列声波测井资料处理方法，其处理结果稳定，但精度有待提高。康晓泉等[10]提出慢度—距离相关法，其计算量比STC少，精确度有所提高。王雷等[11]利用STC法以及n次方根法对多种不同分辨率的接收器阵列组合进行了纵横波时差提取研究。

模拟退火算法是一种随机智能优化算法，由Metropolis等[12]于1953年提出。1983年，Kirkpatrick等[13]成功地将退火思想引入到组合优化领域，解决了诸如流动销售以及复杂电路集成设计等问题。模拟退火(SAA)算法在地球物理领域首先被应用于地震解释，后来又相继在电法以及重力反演中使用。在测井数据处理与解释中，陶果等[14]提出用模拟退火算法计算横波时差。王飞[15]利用模拟退火算法进行了地层各向异性的反演。赵瑞平[16]引入混沌—模拟退火算法求解超定线性方程组并对储层进行评价。李忠新等[17]将快速模拟退火算法应用于核磁差谱分析中。姜明等[18]将非均匀采样的模拟退火算法应用于随钻电磁波电阻率测井检波系统。

模拟退火算法跳出局部较小的能力强，在阵列声波测井复杂信号处理中具有一定的优势。为了确保结果收敛到全局最优，提高测井解释的精度，本文尝试将模拟退火算法与STC方法结合进行阵列声波不同组分波慢度的提取。

笔者首先对模拟退火算法以及慢度—时间相关法的基本原理进行介绍，然后对两种算法的结合进行分析与探讨，并处理实际数据以验证算法的可行性。之后对T井数据进行各组分波慢度提取，并与STC方法处理结果以及常规测井数据进行对比，验证结果的正确性，最后对该方法的特点进行总结。

1 基本原理

1.1 模拟退火

1) 冷却进度表。常用的冷却方式见表1。

表1中，T0为初始温度，T为当前温度，k为迭代次数，c及N为常数。

冷却方式决定降温的快慢。降温速度过快称为淬火，可能会导致最终的原子排列未收敛到全局最优，而降温速度过慢将会影响退火过程的运行效率。因此，应根据实际情况选择合适的降温函数。

表1 冷却进度

2) 产生新原子排列的方式。必须满足产生的原子排列能够覆盖整个可行域，保证结果代表全局最优。其次，产生新原子排列的方式是温度的函数。随着温度的降低，产生的新原子排列的变化范围逐步缩小，如此可避免出现已经收敛到最优原子排列的邻域但是跳出了该邻域的情况。此外还应满足Markov链的要求，即每个新的原子排列只与上一次原子排列有关。并且，Markov链的长度代表了在每个温度下产生新原子排列的次数。

3) Metropolis准则。它是判断是否接受新原子排列的准则。对应每个原子排列，其状态都由一个能量函数来表征。对于当前状态i，其能量函数设为Ei；根据新解产生方式产生的新状态j的能量设为Ej。若满足EjEi，则按照Metropolis准则依概率判断是否接受新的原子排列。概率计算方式如下：

P=exp[(Ei-Ej)/cKT] 。

(1)

式中：K为Boltzmann常数，T是当前温度，c是常数。此时产生一个0～1之间的随机数，若概率P大于该随机数，则接受新的原子排列；若概率P不大于该随机数，维持当前的原子排列。

1.2 慢度—时间相关法

慢度—时间相关法由Kimball和Marzetta[3]提出。它是一种时域算法，通过比较时窗内固定长度波形的相似性得到组分波的慢度。STC法的具体实现过程如下：首先根据采用的阵列声波测井仪器获得仪器的几个固有参数，即接收器的个数、相邻接收器之间的间距以及采样时间间隔。在整个阵列声波波形上，设置好窗口的长度后，在波至点以及相应组分波慢度范围内分别选择两个值。波至点的位置决定窗口的位置，而慢度的大小决定除第一个接收器之外其余接收器波形的时移长度。以该波至点以及慢度计算相关系数。遍历整个波至点范围以及慢度范围后，以固定的步长移动窗口重复上述计算。将窗口移动足够多次后，将相关系数进行比较，相关系数最大值处对应该组分波最可能的波至点和慢度。计算相关系数的方式如下：

中学阶段，学生尚处在被监护期，开展定向越野运动前要先获得监护人的允许才可向学校申请举办。但目前为止，定向越野运动在校园外的普及程度有限，许多监护人对定向越野运动缺乏足够的认识，监护人的不重视导致了学生参与定向越野运动的机会较少。

(2)

式中：M为该阵列声波测井仪器接收器的个数，一般为8；T是波至点；Tw是窗的长度，根据实际波形长度选取；s是慢度，rm(t)为第m个接收器的波形，z1为第1个接收器到发射器的距离，zm为第m个接收器到发射器的距离。

1.3 模拟退火算法与慢度—时间相关法的结合

为了将模拟退火算法应用于阵列声波组分波慢度提取，首先关注其可行性。对照物理退火与组分波慢度提取过程的相似性，原子排列相当于组分波的慢度，亦即反演过程的解。而最终的原子排列相当于最可能的组分波慢度，亦即最优解。所有的原子排列方式组成了整个反演过程的解的可行域，即慢度搜索范围。原子排列的变化相当于波至点以及慢度值的更新。某种原子排列的能量函数对应于反演的目标函数，也可以理解为解的合理性。能量函数(目标函数)值越小，解越合理。

通过以上分析可知，将模拟退火算法应用于阵列声波组分波提取具有可行性。下面对能量函数的设计进行讨论。能量函数应该能够表征解的优劣，而慢度—时间相关法的相关系数即是该组分波波至点以及慢度优劣的表征。然而随着降温过程的进行，能量应该逐渐降低，而相关系数的值增大才能说明解更加合理。因此，对慢度—时间相关法的相关系数进行变换：

E=1-ρ2(s,τ) 。

(3)

变换后，慢度与波至点数值越接近真实值，对应的能量越小，从而能够符合退火过程能量函数的特点。

将慢度—时间相关法的相关系数进行简单变换作为模拟退火算法的能量函数，完成了两种算法的结合。然后按照模拟退火规则进行处理即可进行阵列声波组分波慢度的提取。

2 算法流程与实现细节

以Microsoft Visual C++为平台进行程序编写。算法的流程如下。

1)导入原始波形数据。对原始数据进行预处理。预处理分为3步：去增益、滤波以及均衡化。去增益的目的是恢复原始波形的真实幅度；滤波的目的是去掉各种噪声干扰；均衡化的目的是调整不同接收器的波形，使各接收器的波形变化幅度接近，便于进行相关对比。

滤波是整个预处理中最重要的环节，它对处理结果的影响最大。由图1，滤波后信号信噪比获得了明显提升，能够从图上分辨出纵波、横波以及斯通利波，而且波形更加规则、圆滑。

图1 滤波前(a)后(b)波形对比Fig.1 The comparison of waveforms before(a) and after(b) filtering

2) 给定相应的常数值并为各变量赋初始值。常数值包括数据的行数、列数、接收器的个数、相邻接收器值之间的间距、窗时移次数、窗口长度、窗时移步长、Boltzmann常数、系统初始温度、终止温度、Markov链的长度、慢度以及波至点搜索区间的初始值以及乘积因子c。窗时移次数、窗口长度以及窗时移步长将影响计算的能量值。系统初始温度、终止温度、Markov链的长度可以根据程序运行情况进行调整，在能够保证结果精度的基础上，适当的减小初始温度，增大终止温度，缩小Markov链的长度，从而提高算法的运行效率。经过多次试验发现，初始温度设置为10，终止温度设置为1时，即可较快地得到精度合理的结果。选择该区间的原因是初始温度过高将使迭代速度变得很慢，而初始温度选择过低无法保证获得最优解。乘积因子c作用在Metropolis判定准则上，其目的是影响接受概率，保证在较高的温度下，接受能量增加的解的概率大一些；并且随着温度降低，接收能量增加的解的概率减小。

3) 对于不同组分波以不同方式处理。由于纵波是首波，其波至明显，易拾取，故对纵波首先采用长短时窗能量比法进行波至点的求取，然后进行慢度的一维搜索以便提高算法运行速度。长短时窗能量比法的原理在此不再赘述。横波以及斯通利波在波列上处在纵波之后，可能发生混叠，其波至点位置提取不准，因此，采用波至点—慢度的二维搜索。

4) 选定要提取的组分波，以快速降温方式进行模拟退火。在可行解空间中选择初始值。本文中波至点以及慢度初始值皆选择整个搜索区间的中点。将初始值作为当前解计算其能量值。根据新解产生方式产生新的波至点以及慢度值，计算其能量值。根据状态接受函数判断是否接受，若新解能量小于当前解，则直接接受新解；否则，按照Metropolis准则进行判断，若计算的概率大于产生的随机数，则接受新解；否则，维持当前解。判断是否达到Markov链的长度，若不满足，继续进行“产生新解—判断—接受/舍弃”的过程，若满足，进行降温。在下一个温度重复该过程，达到Markov链的长度即进行降温。判断当前温度是否小于结束温度。若不满足，继续降温；若满足，则终止整个迭代过程，进行下一个深度点的计算。算法整体流程如图2。

3 实际数据处理

按第2节的流程对L井进行纵波慢度提取，其结果如图3，数据选自1 545～1 560 m深度段。在1 550 m以下的深度段，本算法处理结果与STC方法处理结果皆与常规纵波测井数据吻合得很好。在1 550m以上的深度段，STC方法得到的结果过于平缓，无法精确地反映地层声速的变化。本算法处理结果与常规测井曲线更加接近，虽然不能完全重合，但是更能够反映地层声速的细微变化。本算法处理的结果与常规纵波测井的平均绝对误差为-1.37 μs/ft，平均相对误差为-1.26%；而STC方法处理结果与常规测井的平均绝对误差为-1.92 μs/ft，平均相对误差为-1.68%。本算法结果的平均绝对误差比STC方法的处理结果小0.55 μs/ft，平均相对误差比STC方法的处理结果小0.42%。因此，本算法的纵波结果更加贴近常规测井。

图2 算法流程Fig.2 The flow diagram of the algorithm

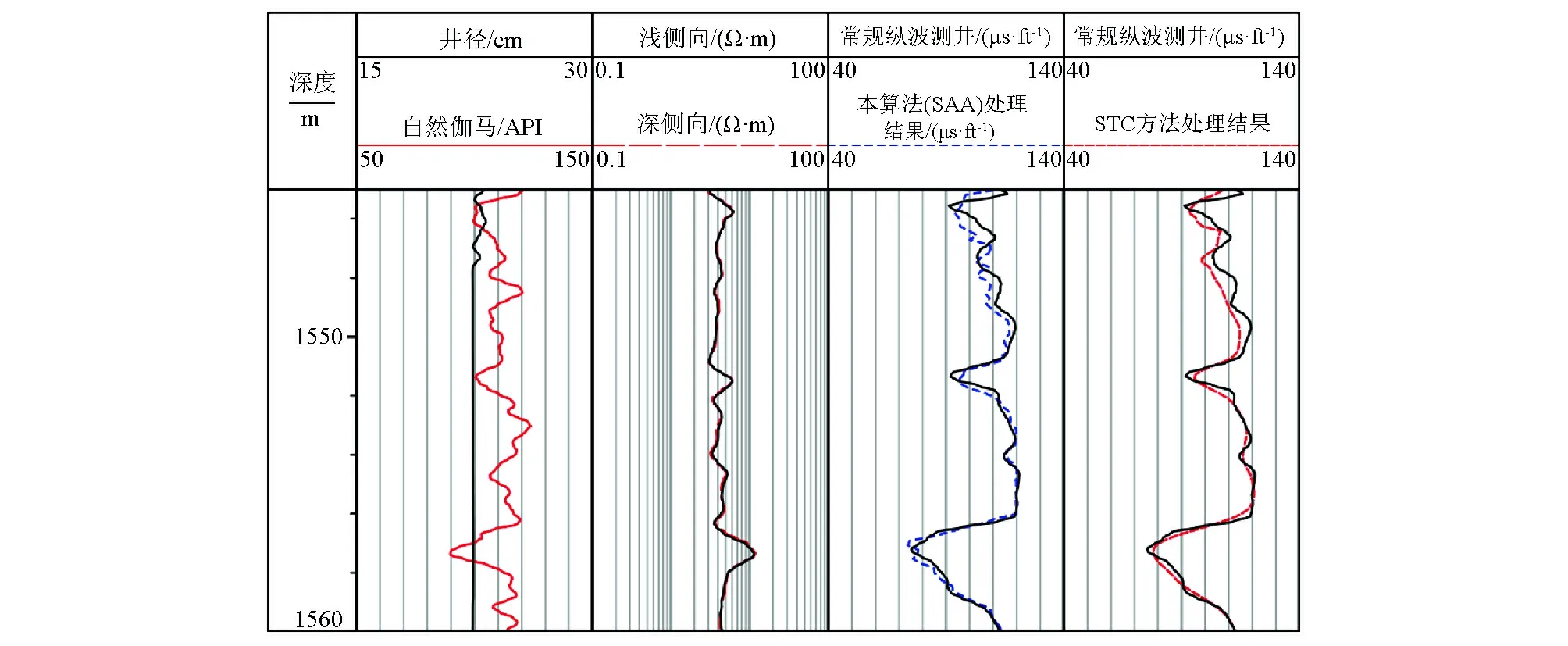
图3 L井纵波处理结果Fig.3 Processed results of compressional wave in well L

由以上结果可知，本算法提取的L井阵列声波纵波慢度结果优于传统STC方法。为检测算法的普适性，将其应用于其他井进行数据处理。为验证算法提取不同组分波的效果，分别对纵波、横波、斯通利波进行了慢度提取。

选取T井单极子数据进行组分波慢度提取，其结果如图4。为了检测算法鲁棒性，本数据选自T井2 062.5～2 082.5 m总计20 m的深度段，该深度段的声速变化范围较大，而且变化较剧烈。可以看到，井径曲线良好，仅在2 078 m附近出现略微的扩径。自然伽马曲线变化不大，自然电位曲线非常平缓。该井段孔隙度一般在10%～15%范围内。深浅侧向曲线非常接近，没有明显的异常。

常规声波测井源距短，接收器间距小，处理的结果更能反映地层的变化，曲线跳动较剧烈，容易受到环境影响。由井径的变化趋势可知，该深度段受扩径的影响很小。本算法与传统STC方法都能够提高信噪比，但是在一定程度上损失了地层的分辨率。因此，曲线整体变化趋势较常规测井圆滑一些。对于纵波，在2 063～2 065m深度段，常规测井结果呈现“高—低—高”的趋势，本算法处理结果与常规测井结果一致，而传统STC方法处理结果仅出现了一个明显的峰。在2 076～2 080 m深度段，STC方法处理结果曲线过于圆滑，对于声速的细微变化刻画的不好。在2 080～2 081 m深度段，本算法处理结果与常规测井结果变化趋势一致，吻合度更高，而STC方法处理结果呈现一个圆滑的峰。从整体上看，本算法得到的结果曲线的趋势与常规测井更加接近；传统STC方法的处理结果相对于本算法结果以及常规数据更加圆滑，其描述声速细微变化的能力不足。本算法与常规测井结果平均绝对误差为-1.23 μs/ft，平均相对误差为-1.45%；传统STC方法与常规测井结果平均绝对误差为-1.43 μs/ft，平均相对误差为-1.61%；本算法的平均绝对误差值减小了0.2μs/ft，平均相对误差优于STC方法9.94%。从误差分析角度来看，本算法得到的误差更小，与常规测井结果更加接近。对于横波，由于常规测井中没有横波数据，故将本算法的处理结果与传统STC方法的处理结果进行横向对比。本算法结果与传统STC方法处理结果的平均绝对误差为0.40 μs/ft，平均相对误差为0.29%。从图上可以看出，两者整体的变化趋势几乎完全相同，结果非常接近。对于斯通利波，也将本算法的处理结果与传统STC方法的结果进行横向对比。从整体上看，本算法处理得到的斯通利波慢度变化趋势与传统STC方法的结果比较接近；与其他曲线进行对比发现：在2 063～2 065m深度段，本算法提取的斯通利波慢度变化趋势比传统STC方法的结果更加接近常规纵波曲线的变化趋势。本算法结果与传统STC方法结果的平均绝对误差为-0.96 μs/ft，平均相对误差为-0.42%。从误差分析角度来说，两结果相差不大；从图上直观地看，本算法处理的结果更能够反映地层声速的细微变化。综合考虑3种组分波处理结果，认为本算法能够更好地表征地层声速特征。

图4 T井各组分波处理结果汇总Fig.4 The overall processed results of component waves in well T

4 结论

阵列声波测井组分波慢度提取算法较多，目前的算法如传统慢度—时间相关法已经被广泛使用于组分波慢度提取。本文尝试将模拟退火算法与慢度—时间相关法结合，对目前算法进行进一步改进，并得到以下结论：

1)模拟退火算法由于其固有的全局寻优能力，能够跳出组分波慢度提取相关系数(能量)计算过程中的局部极小，从而得到优于传统STC方法的结果。

2)对于纵波，本算法与常规测井数据的对比结果显示出一定程度的精度提升。对于横波，本算法处理结果与传统STC方法结果非常接近，其精度与传统STC方法持平。对于斯通利波，本算法处理结果与传统STC方法结果有一定的差异，由于缺乏地层真实斯通利波数据，其精度是否有所提升有待进一步探讨；考虑到其曲线变化特征与常规测井曲线的变化趋势更加接近，认为本算法相比传统STC方法过于圆滑的处理结果更符合实际地层特征。

3)本算法注重提升解释精度。后续可进行程序的优化，从而进一步提高其运行速度，达到快速精细解释的目的。