非正规子群链长为3 的有限p 群

贺丽娟，李璞金

山西师范大学数学与计算机科学学院，山西临汾041000

0 引言

正规子群是有限群的基本概念，它源于著名的Galois 理论中的正规扩张的概念. 早在1897 年，Dedekind 就在文献［1］中确定了所有子群都正规的有限群，这类群后被称为Dedekind 群. 研究比Dedekind 群更广的群类问题是群论学者研究的热点问题之一，例如见文献［2 ～7］等.值得一提的是，著名群论学家Passman 的经典p 群论文［3］.该文中他研究了非正规子群阶的可能性并提出了非正规子群链的概念:

以M(G)，m(G)的术语，Passman 在文献［3］中分类的是M(G)- m(G)= 0 的p 群;安立坚分类的是M(G)- m(G)≤1 的p 群. 本文继续安立坚在文献［2］的工作，分类了M(G)- m(G)= 2 的特殊情况.

本文旨在研究p ＞2 时，非正规子群的阶为pm，pm+1，pm+2(m ≥3)的有限亚Hamiltonp 群.主要结果见本文的定理1 与定理2.

1 预备知识

引理1［7，引理2.4］ 设E 是有限p 群G 的内交换子群.若［G，E］= E'，则G = E* CG(E).

定义2［8，定义12.2.1］ 设G 是有限非交换p 群，称G 是亚Hamiltonp 群，如果G 的每个子群或交换或正规.

引理2［8，定理2.3.6］ 设G 是有限p 群. 则下列命题等价:

(1)G 是内交换群;

(2)d(G)= 2 且| G' | = p;

(3)d(G)= 2 且Z(G)= Φ(G).

2 非正规子群链长为3 的有限p 群

由文献［2，定理9.1］可知，P 群均为亚Hamilton p 群. 文献［定理3.1，定理4.1］给出了有限亚Hamilton p 群的分类. 因此分类非正规子群链长为3 的有限p 群，本文只需从有限亚Hamilton p 群的分类中挑出满足条件m(G)≥3，M(G)- m(G)= 2 且chn(G)= 3 的群即可.

引理3 设G 是有限p 群，p ＞2，| G' | = p.若m(G)≥3 且M(G)- m(G)= 2，则d(G)≤4.

证明 显然G 非交换.设H 是G 的内交换子群.根据引理1 可设，G = H* CG(H)，其中H ∩CG(H)≤H'.又设d(G)= t.下证t ≤4.若否，则t ≥5.此时不妨可设

(4)(Mp(n，m)* Cp2)× Cp，其中n ≥m ≥3.

证明 ⇒ 根据引理3 可知，d(G)≤4.因此我们只需考虑2 ≤d(G)≤4 的情况.

下面将分三种情形进行讨论.

情形1 d(G)= 2.

显然G 是内交换群. 故G ≅Mp(m1，n1)或G ≅Mp(m1，n1，1).

若G ≅Mp(m1，n1，1)，则m1≥n1≥3 且n1≥3.但此时G 同构于文献［10，定理3.2］的群(1)，其中m1≥3，n1≥3 的情形. 因此chn(G)≤2，矛盾.

情形2 d(G)= 3.

此时，G 同构于下列互不同构的群之一:

(i)Mp(m1，n1)× Cpk，其中m1≥2，n1≥1，k ≥1;

(ii)Mp(m1，n1，1)× Cpk，其中m1≥n1≥1，k ≥1;

(iii)Mp(m1，n1，1)× Cpk，其中Mp(m1，n1，1)∩Cpk= M'p(m1，n1，1)，m1≥n1≥1，k ≥2.

若G 同构于群(i)，不妨设G =〈a，b，c| apm1= bpn1= cpk= 1，［a，b］= apm1-1，［c，a］=［c，b］= 1〉，其中m1≥2，n1≥1，k ≥1.

情形3 d(G)= 4.

显然G 是非交换群，故G 中必存在内交换子群，不妨设为H.根据引理1 可设，G = H* CG(H)，其中H ∩CG(H)= G'.因为d(G)= 4，故不妨可设G =〈a1，a2〉*〈a3，a4〉其中H =〈a1，a2〉，|〈a3〉| = pk，| 〈a4〉| = pl，k ≥1，l ≥1.由引理3 可知，H ≅Mp(m1，n1)或H ≅Mp(m1，n1，1).

若H ≅Mp(m1，n1)，类似可知，m1≥3，n1≥3.若H ≅Mp(m1，n1，1)，同理m1≥n1≥3.

又注意到〈a1，a2〉∩〈a3，a4〉≤G'，因此下面分〈a1，a2〉∩〈a3，a4〉= 1 和〈a1，a2〉∩〈a3，a4〉= G'两种子情形进行讨论.

情形3.1 〈a1，a2〉∩〈a3，a4〉= 1.

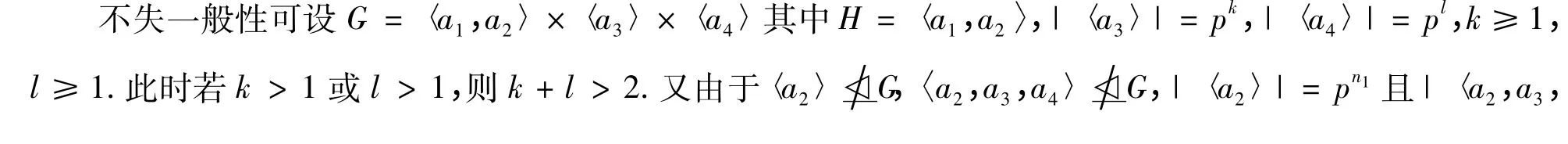
综上可知，p3≤| H|≤p5.又容易计算知〈b〉≤〈b，ap2〉≤〈b，ap〉为G 的一条非正规子群链.

若G 群同构于群(2)～群(4)之一.类似群(1)的证明方法，可证pm≤| H|≤pm+2.对于群(2)而言，计算知〈b〉≤〈b，cp〉≤〈b，c〉为G 的一条非正规子群链.对于群(3)而言，又容易计算知〈b〉≤〈b，c〉≤〈b，c，d〉为G 的一条非正规子群链. 对于群(4)而言，不妨设为又容易计算知〈b〉≤〈b，apn-2c-1〉≤〈b，apn-2c-1，d〉为G 的一条非正规子群链.

综上可知，定理中的群(1)～群(4)满足chn(G)= 3 且非正规子群的阶仅为pm，pm+1，pm+2.定理的证.

定理2 设G 是有限p 群，| G' | ＞p. 则G 是P 群当且仅当G 同构于下列互不同构的群之一:

(1)〈a，b| apn= bpm+1= 1，［a，b］= apn-2〉，其中n ≥m +1 ≥4;

(2)〈a，b，c| ap3= bp3= cp3= 1，［a，b］= cp2，［a，c］= bvp2，［b，c］= 1〉，v 是某固定的模p 平方非剩余;

(3)〈a，b，c| ap3= bp3= cp3= 1，［a，b］= cp2，［a，c］= bkp2，［b，c］= 1〉，1 +4k ∉(Fp)2.

证明 ⇒ 设p ＞2 | G' | ＞p. 当exp(G')＞p 时，根据引理［2，推论5］可得定理中的群(1). 当exp(G')= p 时，G 同构于文献［9，定理3.1，定理4.1］的群(B1)～群(B8)，群(C3)～群(C10)，群(D1)，群(D2)，群(D4)，群(D5)之一.又因为G 的p 阶子群均正规，所以c(G)= 2.显然群(B1)～群(B8)不符合条件.因此只需考虑G 同构于群(C3)～群(C10)，群(D1)，群(D2)，群(D4)和群(D5)之一.下面逐一讨论.

综上所述，定理得证.