线性时变周期系统的保性能控制

朱灿，焦淑云*

1. 山西师范大学现代文理学院数学与计算机科学系，山西 临汾041000;

2. 山西师范大学数学与计算机科学学院，山西 临汾041000

在物理以及工程技术中，很多问题都可以最终转化为具有周期系数的线性微分方程组.例如，激光物理以及天体力学的数值问题、卫星的姿态控制问题、直升飞机的传动系统以及经济系统与生态系统中的周期环境竞争平衡等问题［1］.

线性时变周期(LTVP)系统是一类复杂而又重要的系统，该系统近些年来，引起了众多的关注. 文献［2］研究了离散周期系统模型匹配的问题，而Vicente［3］研究了离散周期系统的极点配置的问题，并且成功地利用周期输出反馈来配置出周期系统的单值矩阵的极点.张雪峰［4］研究了线性时变周期系统的稳定性和鲁棒控制，并给出了LTVP 系统稳定性的充要条件以及相应的LTVP 系统的鲁棒镇定控制器的设计.

尽管近年来，国内外学者对LTVP 系统展开了多方面的研究，其中，不乏许多重要且独特的见解. 但是，在设计LTVP 系统的控制器时，关于保性能控器问题的研究并不多见.

保性能控制［5］的主要思想针对系统中的不确定性，设计出一种保性能控制器，使得该系统在保性能控制律的调节下，不仅可以保证系统的渐近稳定，还可以使得系统的性能指标满足一定的上界.

因此，本文在研究保性能控制器的设计时，就考虑到了系统需要满足的一些性能指标. 本文致力于LTVP 系统的保性能控制的研究，并且成功地给出了LTVP 系统相应的保性能控制器的设计方法.

1 LTVP 系统简介

考虑一个LTVP 系统［6］

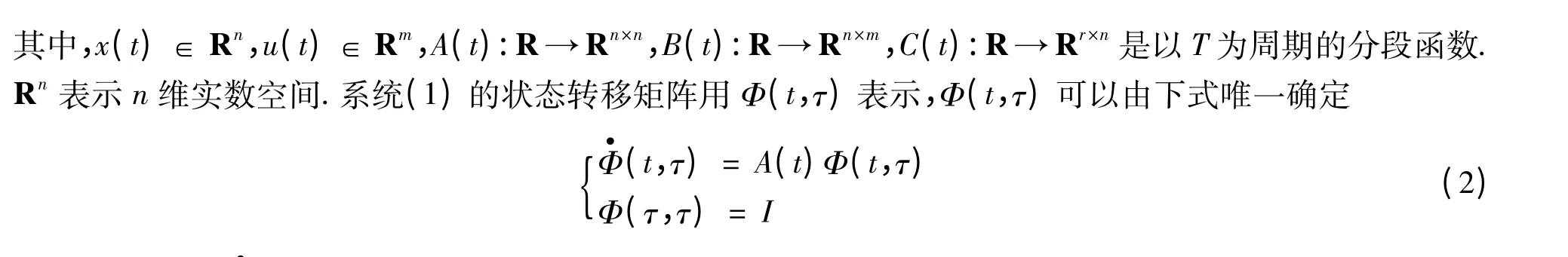
容易得出结论:Φ·(t + T，τ +T)= A(t +T)Φ(t + T，τ + T)= A(t)Φ(t + T，τ + T)且Φ(τ + T，τ + T)=I，即Φ(t + T，τ + T)也满足式(2).

故有Φ(t + T，τ + T)= Φ(t，τ)，而矩阵Φ(T，0)被称为单值矩阵，该矩阵在LTVP 系统中非常重要.利用鲁棒控制的相关思想，可以把LTVP 系统简化成一种范数有界的鲁棒扰动形式.

其中，Q，R 是给定的加权对称正定矩阵.

定义1［8］对LTVP 系统(1)和性能指标(3)，如果存在一个控制律u(t)和一个正数J*，使得对所有允许的不确定性，闭环系统是渐近稳定的，并且，闭环性能指标满足J ≤J*，则J*被称为LTVP 系统(1)的一个性能上界，u(t)被称为LTVP 系统(1)的一个保性能控制律.

下面给出几个必要的引理.

2 保性能控制器的设计

由Lyapunov 稳定性定理可知，闭环系统(6)是渐近稳定的.

进一步，对(7)式两边同时做如下积分，并由系统的渐近稳定性质，可得

不过，定理1 虽然给出系统(6)的保性能控制器的设计方法，但是定理1 所得条件不是基于LMI 的.因此，下面本文将定理1 进一步改进，给出基于LMI 形式的保性能控制器的设计方法.

定理2 对于系统(6)和性能指标函数(3)以及给定对称正定矩阵Q，若存在适当维数的对称正定矩阵X 和矩阵W 以及正常数ε1＞0，ε2＞0，使得对于所有的ΔTi(t)Δi(t)≤I，i = 1，2，有以下矩阵不等式成立

其中，Ω = XAT+AX +WTBT+BW +(ε1+ε2)MMT，I 为适当维数的单位矩阵，“* ”表示矩阵的对称部分，则u(t)= Kx(t)是LTVP 系统(1)一个保性能控制器，并且，相应的一个系统性能上界为

其中，Σ = ATP +PA +KTBTP +PBK + (ε1+ε2)PMMTP，I 为适当维数的单位矩阵，“* ”表示矩阵的对称部分.再对(10)式两边同乘以diag［P-1I I I I］，再令X = P-1，W = KX.最后，再使用一次引理1，即可得到(8)式.定理2 的其余证明部分，与定理1 相同.定理2 证毕.

3 仿真算例

其中

ε1= 253.363 9，ε2= 348.795 7，经过计算可得K = ［- 19.824 4 4.059 2］. 因此，由定理2 知，可选择u(t)= ［-19.824 4 4.059 2］x(t)作为LTVP 系统(1)的保性能状态反馈控制器.

4 结论

本文针对线性时变周期系统，给出了该类系统的保性能控制器的设计方法. 并且对结果进行了基于LMI 的优化.本文的结论，对传统的状态反馈控制器的一些性能指标的优化问题，提供了可行解决方案.最后，本文给出数值仿真的算例，验证了所提出的方法的有效性.当然，其他相关问题还需要进一步的研究.