具有对数势能的Cahn-Hilliard方程的有限元算法
王星星,王旦霞
(太原理工大学数学学院,山西 晋中030600)
1.引言
Cahn-Hilliard(CH)方程是由Cahn和Hilliard提出的一类非常重要的四阶非线性扩散方程,常用来描述二元合金在某种不稳定状态时相的分离和粗化现象[1−3].在过去的几十年里,它被广泛地应用于研究两种浸没式流体的粗化动力学.
Cahn-Hilliard方程的数值解法已经有很多研究,文[4]运用了有限元逼近法,文[5]提出了二阶的Crank-Nicolson格式在空间上采用混合有限元方法,文[6]在空间上采用傅里叶谱方法,文[7]讨论了具有对数势能Cahn-Hilliard方程的解的渐近性和有限维吸引子的存在性,文[8]研究了具有对数势能的Allen-Cahn方程和Cahn-Hilliard方程的误差估计.
本文在时间上运用中心差分格式空间上使用有限元方法,研究具有对数势能Cahn-Hilliard方程的稳定性和误差估计.运用正则性,将对数势能函数F(u)的定义域的范围由(−1,1)扩展到(−∞,∞).最后给出了数值算例来验证相应的结论.
2.模型及其变量
本文研究的Cahn-Hilliard方程具有如下形式:

其中:Ω ∈Rd,d=2;ε是给定的正参数,ut=;n是单位外法向量,u是混合物中某种物质的浓度,w是化学势能.本文中的对数势能如下:[9]
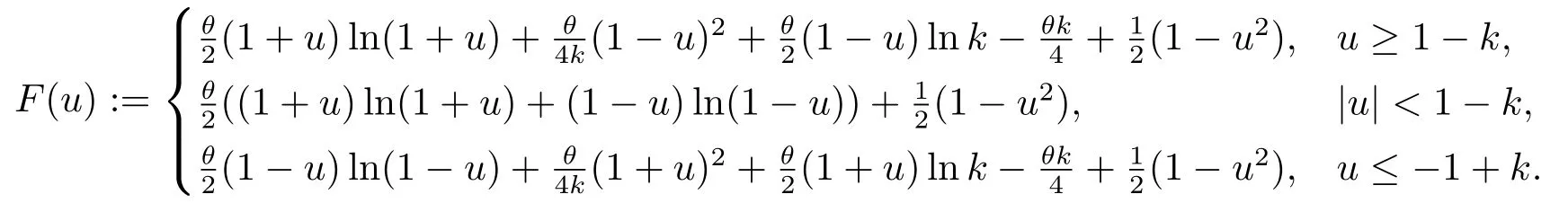
该格式是质量守恒且满足能量耗散定律,对数势能的能量函数定义为:
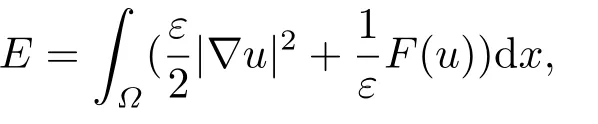
这里θ,k ∈(0,1).
3.离散格式
L2(Ω)是平方可积函数空间,内积范数H1(Ω)是通常的Sobolev空间,半范是范数是∥u∥H1= (Ω|u|2dx+
Cahn-Hilliard方程的弱解形式为:
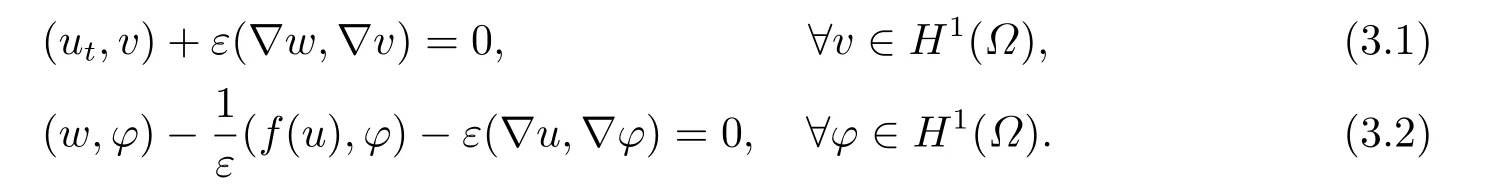
首先把时间区间[0,T]剖分0 =t0 其中 运用泰勒展开,有 设Th=K是区域Ω上拟一致剖分,hi表示网格大小,Sh是分片连续的有限元空间,定义为: 这里Pr(x,y)是x,y的次数不超过r ∈Z+的多项式的集合.此外定义L20:={u ∈L2(Ω)|(u,1)=0},Ŝh:=Sh∩L20(Ω).Cahn-Hilliard方程的全离散格式为:即给定umh,um−1h求um+1h:[0,T]→Sh,当m ≥1,使得: 本文中非线性项是显示处理的,为了保证格式无条件稳定,我们引入两个人工稳定项,则(3.10)变为 Ritz算子Rh:H1(Ω)→Sh满足: 定理4.1令是(3.9)(3.11)的解,当时,对任意的τ,h,ε>0,下面的不等式成立 证在(3.9)中,令,得 (3.11)中,令φh=−(umh+1−umh),得 运用等式 根据(4.2)-(4.5),得 定理(4.1)证毕. 定理4.2设Ξ(u1h)≤C0,存在常数C >0,对于任意的τ,h>0,有下列估计: 证根据(4.1)可得(4.6)和(4.7). 在(3.11)中φh=τ∆2(um+1h −umh) 将上式方程从1到m求和,(4.9)得证. 注定义中的A和B看起来非常大,但在数值模拟时,A和B可以取比定义很小的值. 为了之后证明的简便,我们介绍一些符号: 对于(u,w),我们做如下正则性假设 定义5.1[10]Ritz投影算子满足下面估计 定义5.2H−1范数定义如下: 引理5.1[11]设χ,ψ ∈(Ω),有 引理5.2[12]假设(u,w)是(3.1)-(3.2)的解,则有下面估计: 其中 注 定理5.1设初始问题(3.1)-(3.2),全离散格式(3.9)和(3.11)的解分别是(u,w)和 则存在常数C,C与τ,h均无关,有估计式 (5.6)-(5.7)减去(3.9)(3.11),得 其中 现在我们估计Mi,根据Cauchy-Schwarz不等式,Poincaré不等式和Young不等式 根据Cauchy-Schwarz不等式和引理5.1和5.2 类似地 对于M4,我们有 根据引理5.1,得 对于M6,我们有 结合上述不等式 选择合适的α,将(5.19)带进(5.18)并乘2τ得: 上式从1到m求和,根据离散的Gronwall不等式,有: 在数值实验部分,我们采用一些数值算例验证理论分析的正确性和有效性.选择初始条件为u0=0.5·cos(2πx)sin(2πy)−0.25·cos2(πx)cos2(πy)+0.25·sin2(4πx)sin2(4πy),计算区域为[−1,1]×[−1,1]. 在表1中,选择固定的参数τ= 0.001,T= 0.1,变化的网格步长0.01,θ= 0.1,A= 32,B= 2.相对误差∥ξuh∥H1的空间收敛阶接近于2,与理论部分得到的收敛阶一致. 表1 ε=0.1,θ =0.1 空间收敛阶 图1 T=0.001s 图2 T=0.01s 图3 T=0.1s 图1到图4中,模拟了具有对数势能的Cahn-Hilliard方程的相分离过程,选择固定的参数k=0.01,θ=0.1,h=16,ε=0.2,A=32,B=2,t=0.0001,图中清楚的显示了随着时间的变化相分离的过程.u0=0.1∗rand()−0.05,其中rand()∈[0,1]. 图4 T=0.5s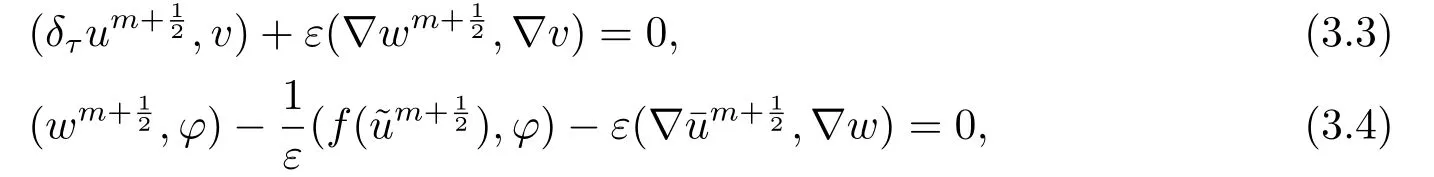
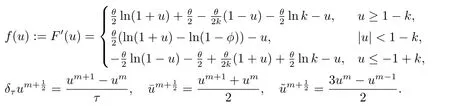
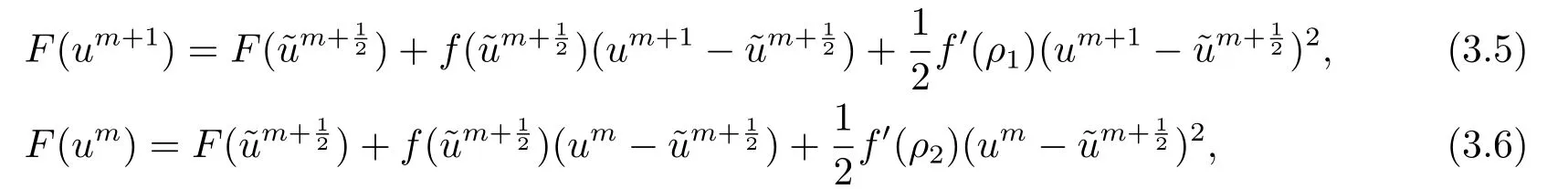
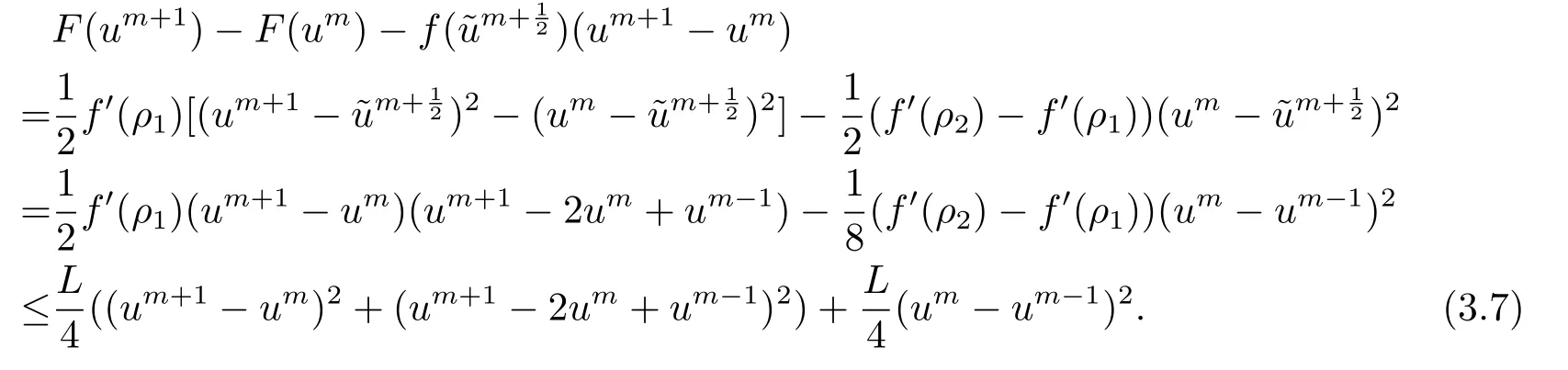
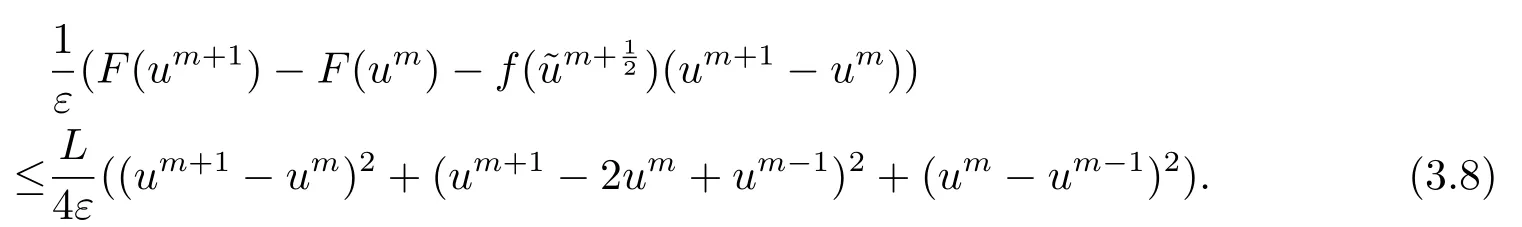

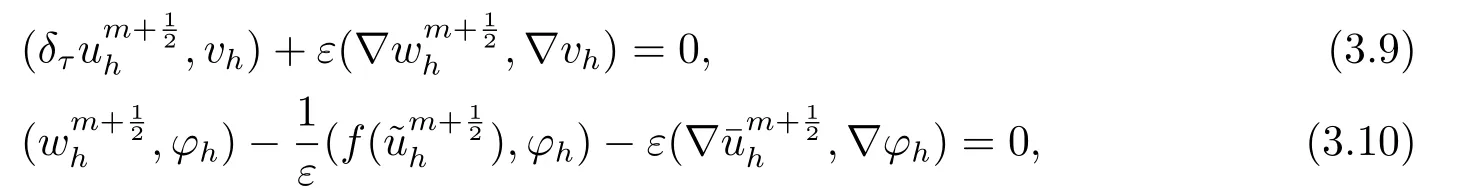
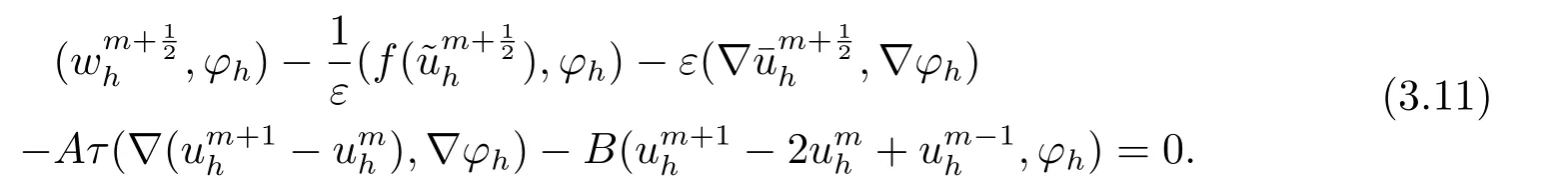
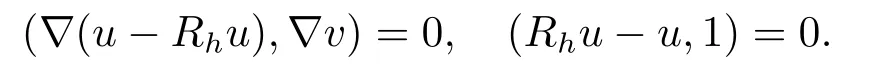
4.稳定性分析
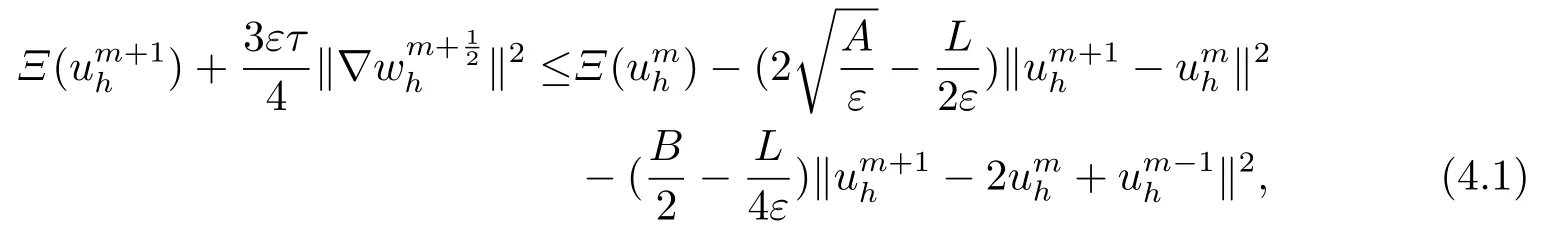
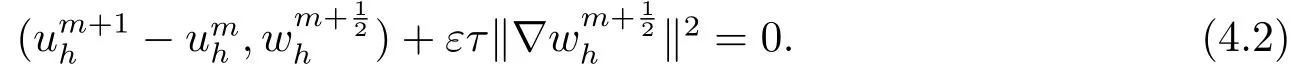
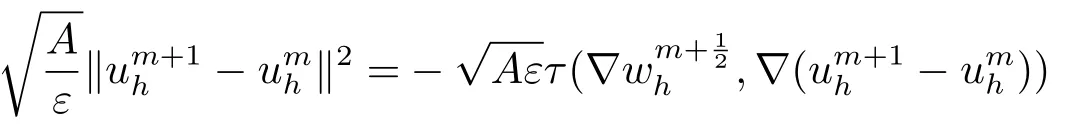
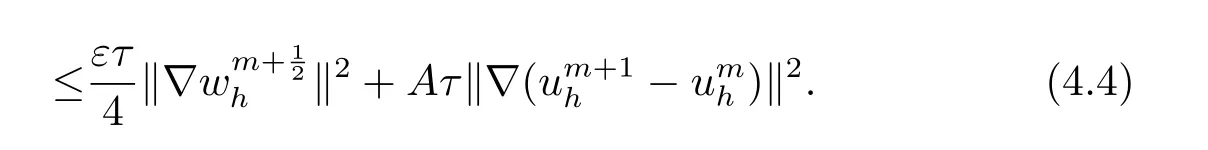
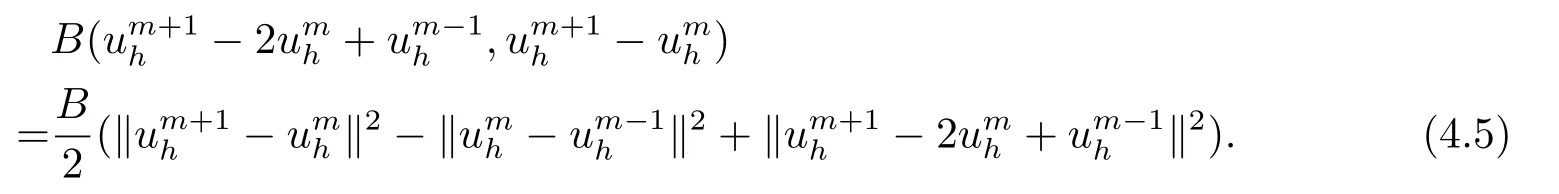
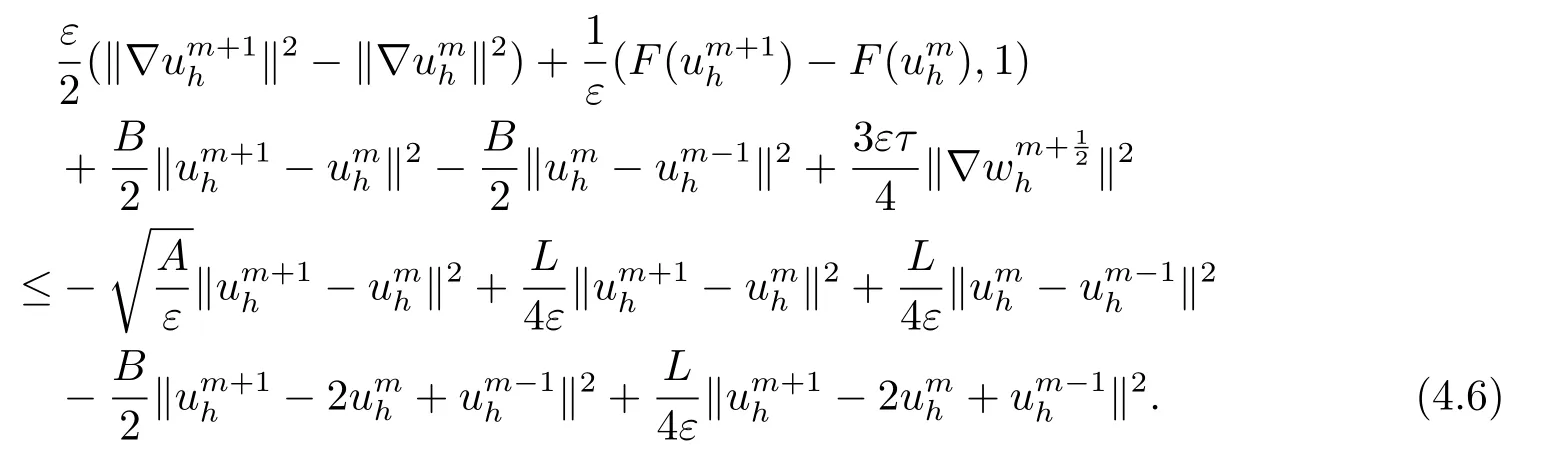
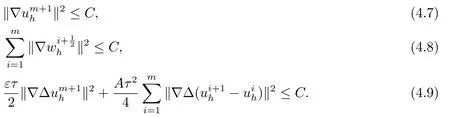
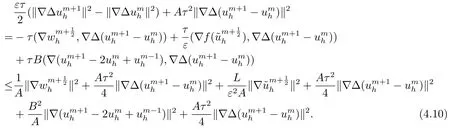
5.误差估计
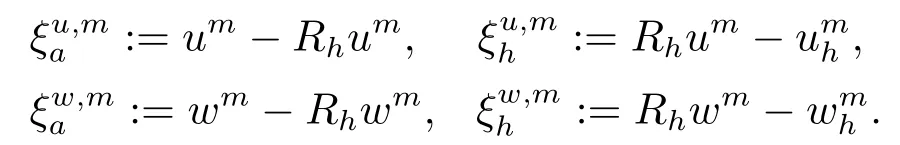
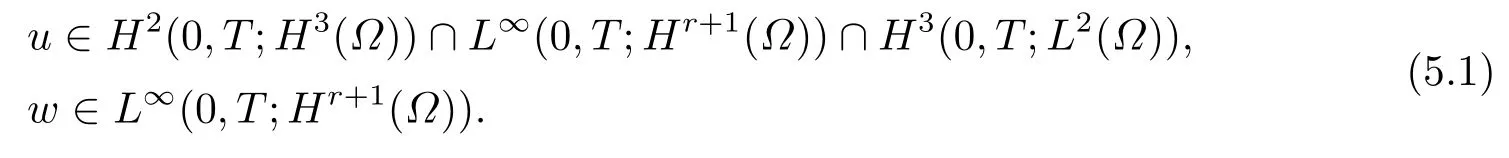
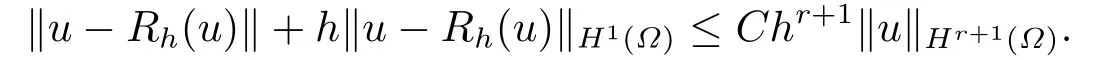
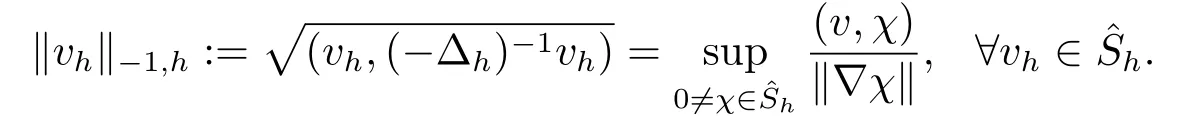
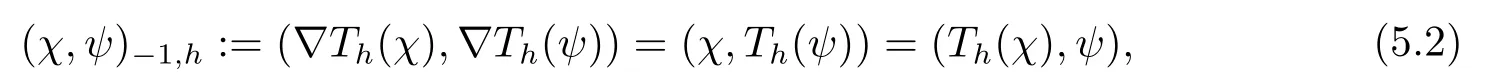
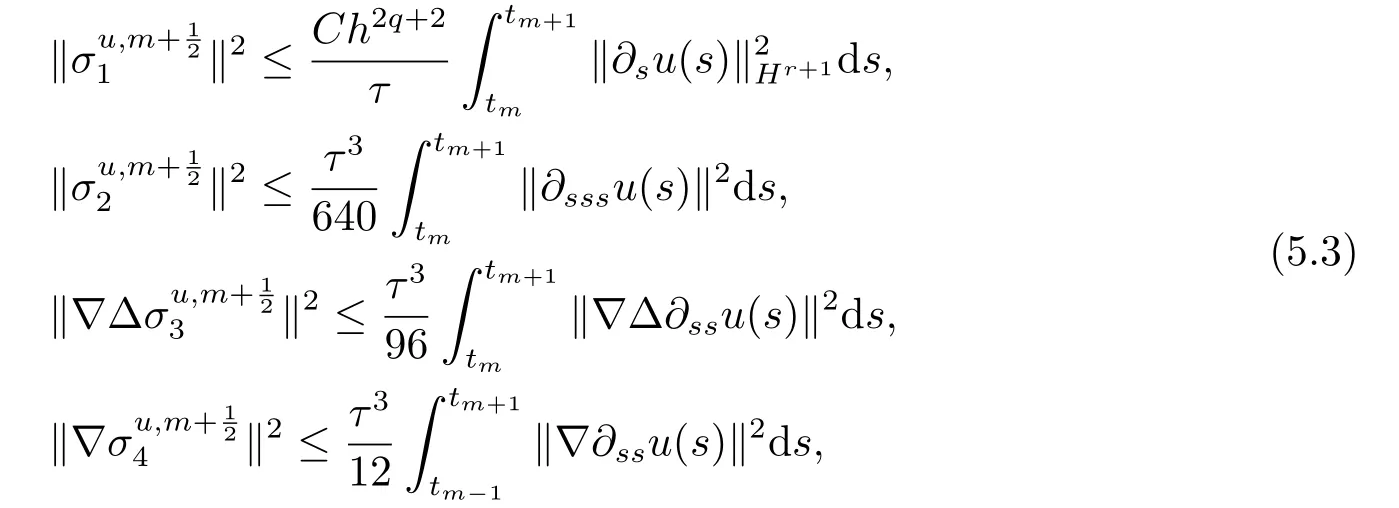
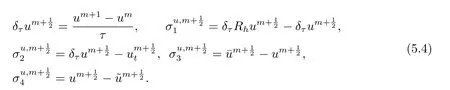
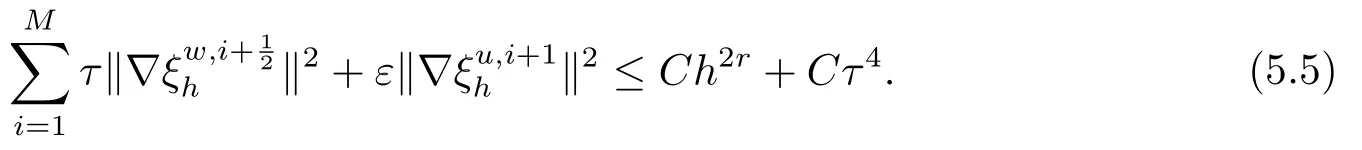
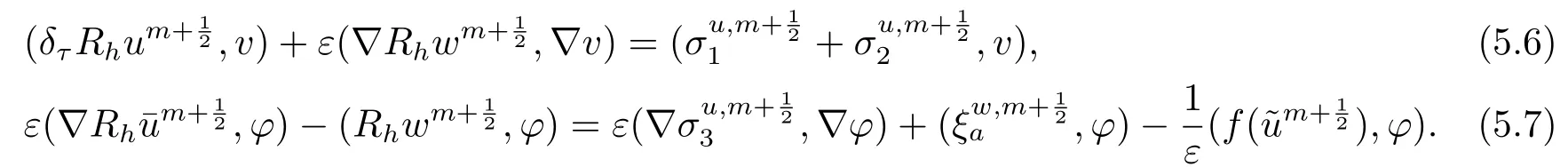
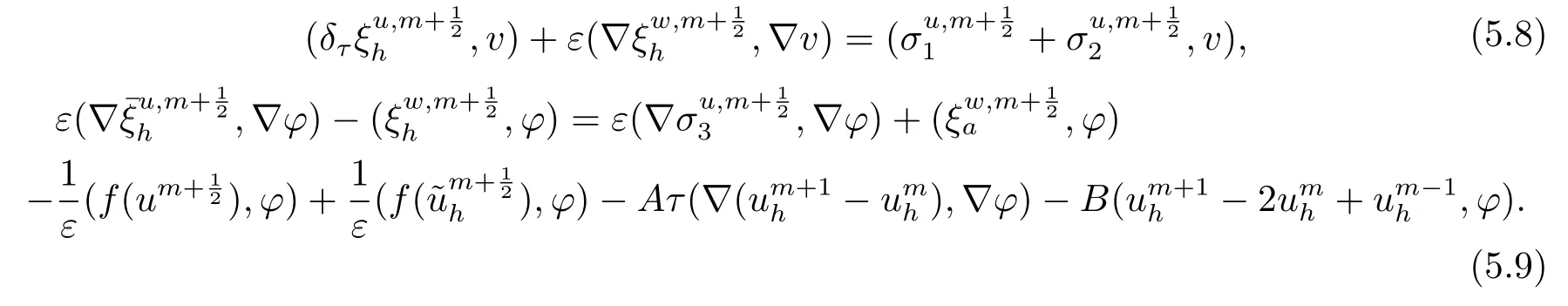
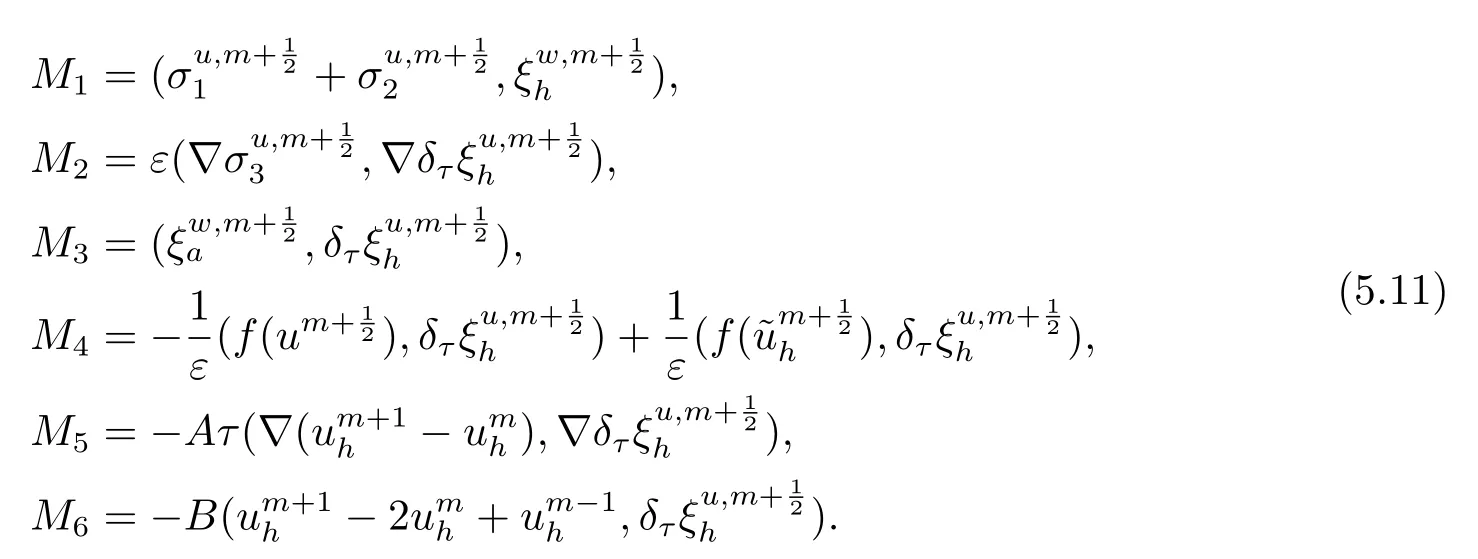
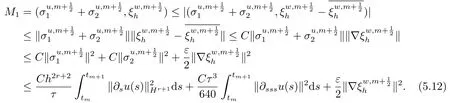
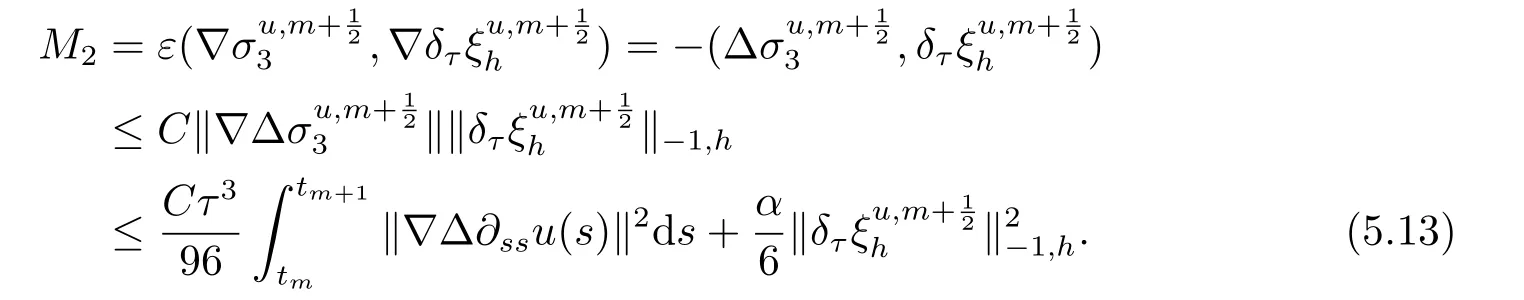
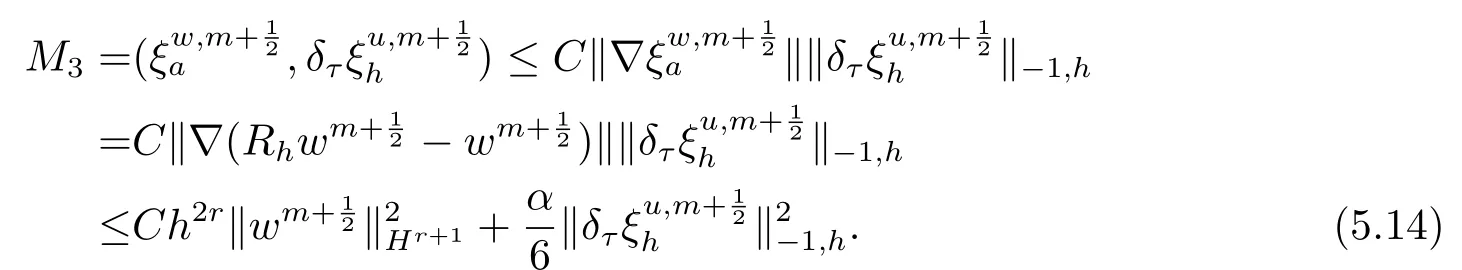
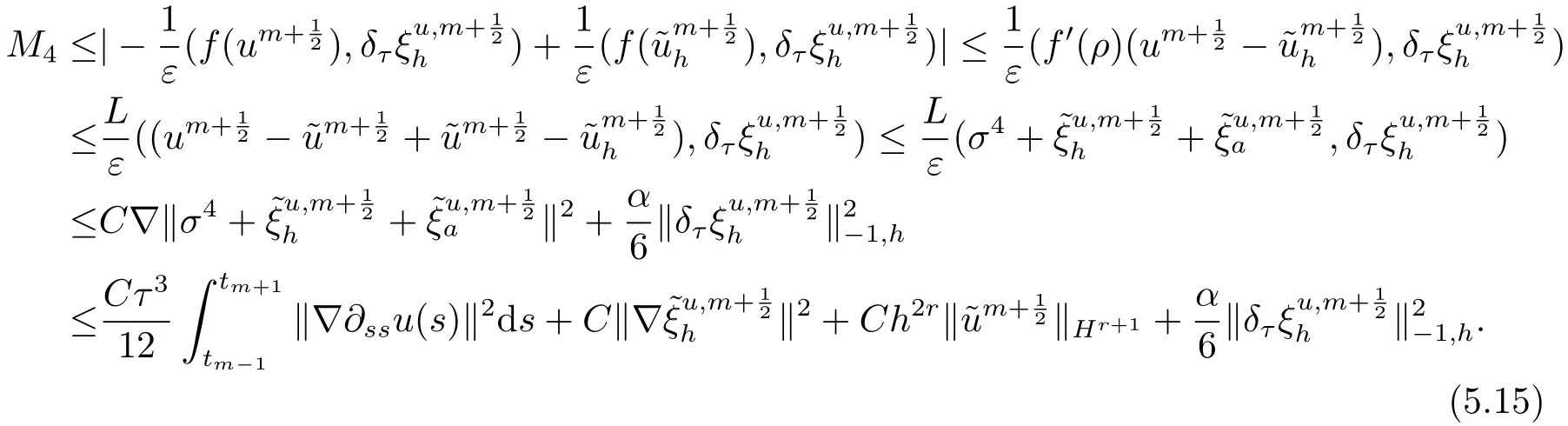
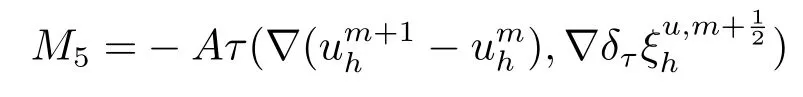
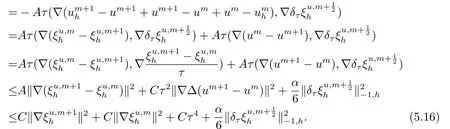
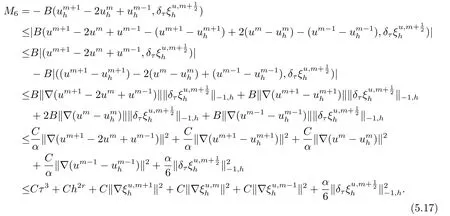
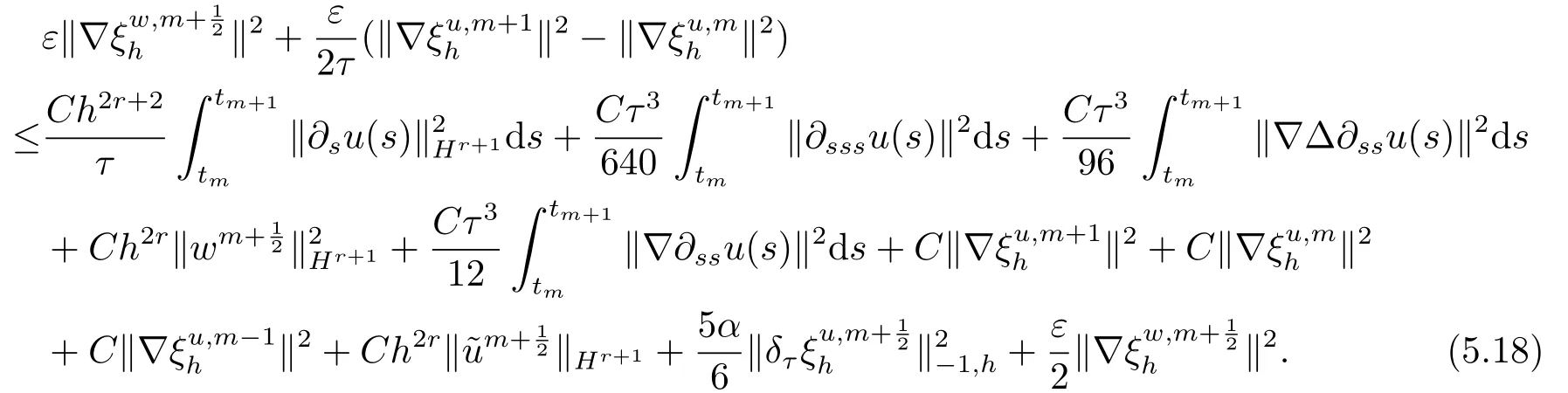
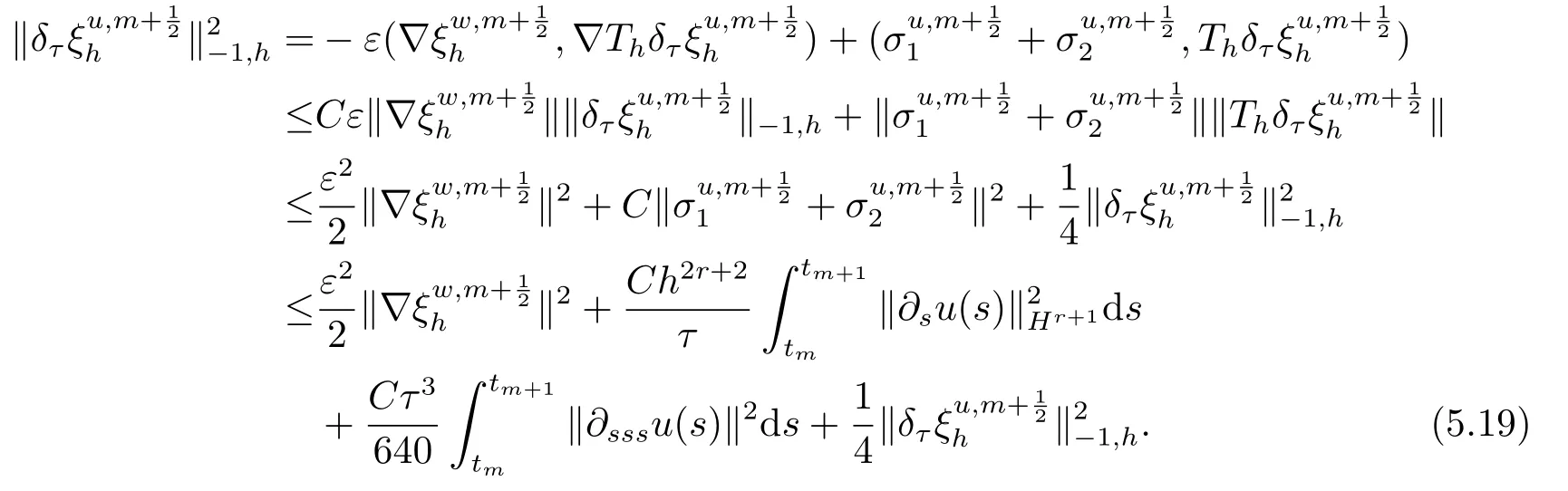
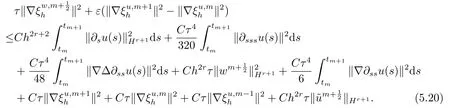
6.数值算例





——《势能》

