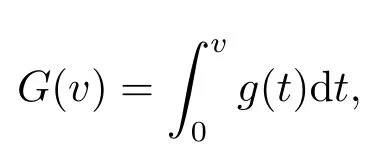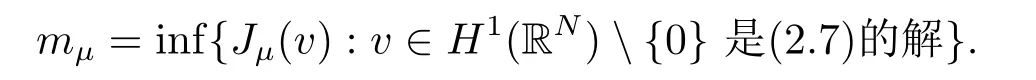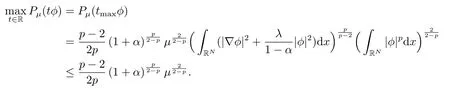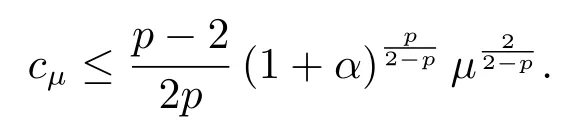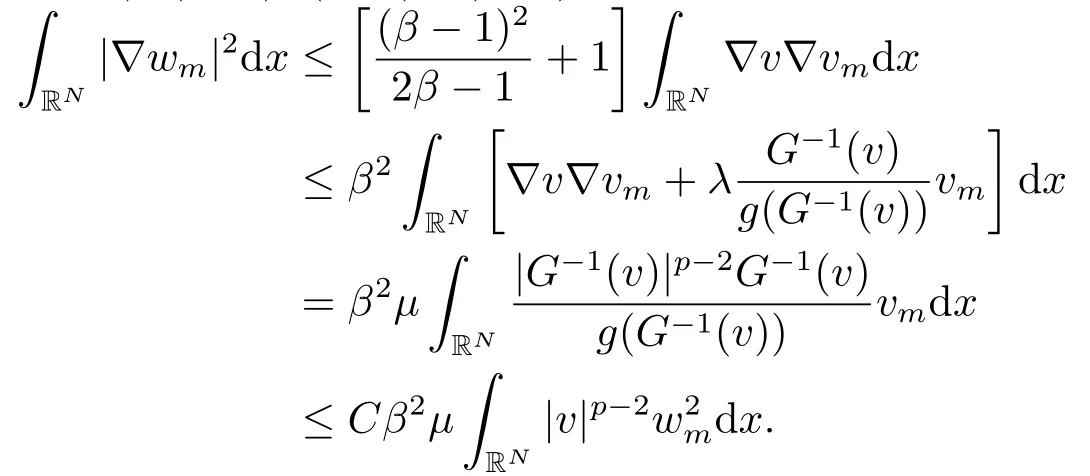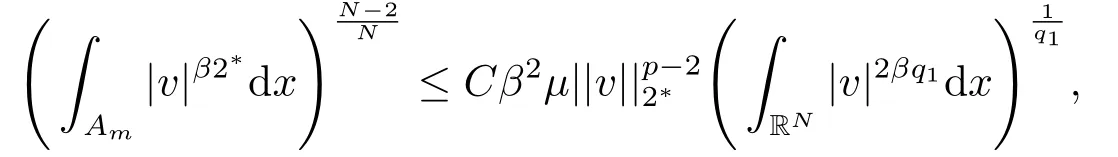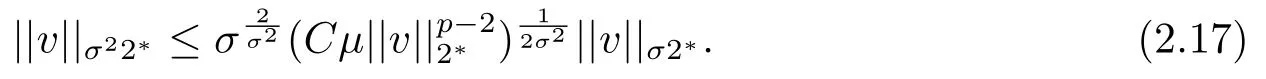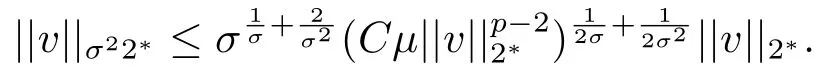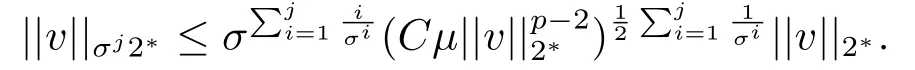广义拟线性Schrödinger方程正解的存在性

于田宁,杨俊

(华南理工大学数学学院,广东 广州510640)

1.问题背景介绍

考虑下列一类广义拟线性Schrödinger方程

其中z(·,·):R×RN →C,ρ(·):R→R是实函数.方程(1.1)可以用来描述很多物理现象和模型.例如,当l(s)=s时,方程(1.1)出现在等离子体物理和非线性光学的各种问题中[1];当时,方程(1.1)可以用来描述高功率超短激光脉冲在等离子体中的自沟道效应[2,3];当时,方程(1.1)出现在经典平面海森堡铁磁自旋链中[4].

本文关注的是方程(1.1)驻波解的存在性,即解的形式为z(t,x)=exp(iλt)u(x),其中λ ∈R,u是实函数.将z(t,x)= exp(iλt)u(x)代入方程(1.1),我们得到一类含变分结构的广义拟线性Schrödinger方程

其中h(u)=ρ(|u|2)u.对于具体的l(s),如l(s)=s或者在最近十余年中,方程(1.2)非平凡解的存在性、多重性以及解的性态得到了广泛的研究.[8−9,12,14]

通过赋予权函数g(s)其合适的条件,方程(1.3)非平凡解的存在性近年来也已被广泛研究.例如：当g(s)∈C1且关于|s|非减时,利用经典的变分理论,文[13]证明了正解的存在性.此外,把λ换成位势函数V(x),以及非线性项h(t)满足次临界条件或者临界条件,关于(1.3)解的存在性已有很多结果,如[10].近期,当g(s)∈C1,关于|s|非增且lim|s|→0g(s)= 0时,文[16]证明了(1.3)正解的存在性.需要指出的是,g(s)的光滑性在上述文献主要结论的证明过程中起到了很重要的作用.换言之,若g(s)1,则文[10,13,16]中处理(1.3)的方法都不再适用.但是,我们注意到有一些物理模型确实满足条件g(s)1,例如,当时,g(s)甚至在[−1,1]外无定义.

因此,一个很自然的问题是：若l(s)只有局部的光滑性,方程(1.2)是否存在非平凡解？

本文的目的是解决上述问题.为此,我们考虑以下模型问题：

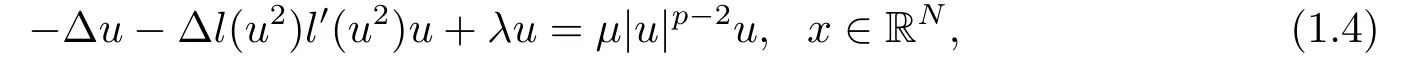
其中λ,µ>0,2

本文的主要结论如下：

定理1.1假设存在δ >0使得l(s)在[0,δ]中有定义,l′′(s)在[0,δ]中连续,20时,存在µ1>0,使得对于µ∈(µ1,+∞),方程(1.4)有一个正的经典解uµ.此外,当µ→+∞时,uµ(x)→0关于x ∈RN一致成立.

注1.2定理1.1中对于l(s)的单调性没有作要求,类似的条件参考文[11,15].

注1.3把λ换成位势函数V(x),在赋予V(x)合适的条件下,利用文[13]中的方法,可以证明定理1.1的结论仍然成立.

注1.4模型满足定理1.1的条件.

本文中符号∥u∥p表示Lp(RN),1≤p ≤∞中的范数.

2.定理1.1的证明

由于l′′(s)∈C([0,δ],R),故对所有的s ∈[0,δ],存在某些C1>1,使得l′(s),l′′(s)

其中0<α<1,可以确保σ的值存在且可取.容易计算

以及

下面引入一个C1辅助函数g(t):

其中η(t)∈C0∞(R,[0,1])是一个截断偶函数,满足条件:当时有η(t)= 1；当t >σ时η(t)=0.此外,存在某个常数C>0使得

关于η(t)的一个具体构造,可参考文[14].

现在令

则其反函数G−1存在且是一个C2函数.

引理2.1以下性质成立：

证1)-3)项可以根据定义直接得出.通过(2.1),(2.2)和(2.3),直接计算得

4)得证.

现在考虑原方程(1.4)的修正方程

下面证明方程(2.4)存在一个正解uµ,且满足则根据g(t)的构造可知,uµ也是方程(1.4)的正解.

方程(2.4)对应的能量泛函为

因为g是有界的,故Iµ(u)在H1(RN)上有定义.通过引入替换变量u=G−1(v),泛函Iµ能被写成

根据G−1(v)的性质,Jµ ∈C1.此外,如果v ∈C2(RN)∩H1(RN)是Jγ(v)的临界点,就有u=G−γ1(v)∈C2(RN)∩H1(RN)且其是方程(2.4)的经典解,参见文[13].

因此,为了找到方程(2.4)的正解,只需研究以下方程正解：

定义

容易验证方程(2.7)右端的项满足文[5]中的条件(1.1),(1.2)和(1.3),因此根据文[5]中的定理1,有以下结论：

定理2.2对于任意的λ,µ>0,方程(2.7)有一个正的轴对称经典解vµ,且Jµ(vµ)=mµ.

定义极小极大值

为了进一步证明uµ=G−1(vµ)是原方程(1.4)的解,我们下面证明当µ充分大时,0

引理2.3方程(2.7)的解vµ满足

证由于vµ是Jµ的临界点,根据引理2.1中性质4),有

即有,

引进辅助泛函：

记

注意到Σµ ⊂Γµ,再根据引理2.1中性质3),有

山清水秀、绿意盎然，石柱县拥有丰富的自然资源和发展乡村旅游的天然优势，这里的万寿山、云中花都、千野草场、大风堡，游人如织、美不胜收……如今，黄水旅游度假区已成为重庆乃至周边省份游客的首选避暑胜地，石柱县也已成为最美中国旅游目的地之一。

再令

则Sp >0可在某个v∗处达到.

现取

则

选择充分大的T >tmax使得Pµ(Tϕ)<0.因此对t ∈[0,1],可得到ξ(t):=tTϕ ∈Σµ使得再根据(2.9)得

引理得证.

根据引理2.3和Sobolev不等式,可得

其中S是最佳Sobolev常数.

引理2.4存在不依赖µ的某个常数>0使得

证这里采用经典的Morse迭代方法.以下为了方便,记vµ为v.对任一m ∈N和β >1让Am={x ∈RN:|v|β−1≤m}且Bm=RN Am.定义

注意到vm ∈H1(RN).使用vm作为一个试验函数,可以推出

除此之外,还有∫

令

然后有

因此根据(2.12)和(2.13),就有

结合引理2.1中性质3),(2.11),(2.12)和(2.14),又由β >1,就有

根据Hölder不等式,且因为在RN中有|wm|≤|v|β,在Am中有|wm|=|v|β,可以得到

取β=σ2在(2.15)中,就有

根据(2.16)和(2.17),有

取β=σi(i=1,2,···)且对(2.15)持续迭代,可得

因此,根据(2.10),使用Sobolev不等式,取极限j →+∞可得

证明结束.

定理1.1的证明令根据引理2.1中的性质3)和引理2.4,可得

定理得证.