一类流固耦合系统强解的存在性问题
谭琳琳,郭真华
(1.西北大学数学学院,陕西 西安710127;2.西北大学非线性研究中心,陕西 西安710069)
1.引言
本文主要研究一类含有多刚体的粘性系数依赖于密度的流固耦合系统强解的存在性问题.刚体在运动中或者受力作用后,形状大小以及内部各点相对位置不变.关于单个刚体――流体耦合系统的研究已经有许多丰富的结果.当粘性不可压缩流体内仅含有单个刚体时,早在上个世纪七八十年代,Judakov[1]便证明了该流固耦合系统全局弱解的存在性.此外,WANG和XIN[2]还对R2上的不可压缩流体与单个不规则刚体的耦合系统进行了研究,得到了二维条件下的W1,p强解的局部存在性.当理想流体与刚体耦合时,似乎获得的结果要少得多.
由于流体和刚体所使用的数学描述框架不同,人们一般使用欧拉坐标描述流体的运动状态,用拉格朗日坐标来描述刚体运动,因此在单刚体――流体耦合系统研究中,研究者常运用坐标转换方法来克服这一难点,但这一方法在面对多刚体――流体耦合时,失去了其有效作用,因此需要寻找其他的解决问题的方法,但本质上解决此类问题的关键步骤是固定流体所占据的区域.
关于多个刚体与流体耦合系统的问题的研究还很少,这是由于刚体的运动是随时间而变化的,使得刚体与流体区域的复杂边界难以处理.当流体含有粘性时,Desjardins[3]建立了对于此类多刚体――流体耦合系统的经典模型.其思想是把刚体近似为粘性足够大的流体,假设流体与刚体接触界面摩擦足够大,即接触界面任意一点的刚体速度与流体速度是一致的,获得了粘性系数为常数,初始密度不包含真空时三维情形下不可压缩流体与多个刚体耦合系统的局部强解的存在唯一性,这种处理多刚体流体耦合系统内的流固边界的方法,为后来研究流固耦合问题所广泛使用.
对于系统初始密度包含真空的情形,由于退化和强非线性,要提高解的正则性就遇到了一系列的挑战.GUO,YANG和YAO[4]在研究气――液两相流模型的柯西问题时,得到了当初始数据的能量足够小时,全局强解的存在性,且结果是允许初始真空的.这给予本文研究工作的一个重要启示,即可以参考非齐次不可压缩流体的Navier-Stokes方程的有关研究.
关于非齐次不可压缩流体的Navier-Stokes方程相关进展,初始密度包含真空的情形已经有大量的研究成果[5−9].特别地,韩国数学家Choe和Kim引进了相容性条件[10−11],来证明非齐次不可压缩流体的Navier-Stokes方程经典解或强解的局部适定性.而后Craig,HUANG和WANG等学者在不同的相容性条件下将结果推广到全局范围.[12−13]另一方面,由于尚未查找到有关粘性系数依赖于密度的该系统的相关研究结果.研究者考虑是否可以在流固耦合问题中讨论粘性系数依赖于密度的情形.而有关粘性系数依赖于密度的明确提法始于文[14].当从Boltzmann方程组通过Chapman-Enskog二阶展开导出Navier-Stokes方程组时[15−16],可以发现其粘性系数和热传导系数都依赖于温度,在等熵的情况下,由Boyle和Gay-Lussac定律可知温度依赖于密度,于是粘性系数依赖于温度转化为粘性系数依赖于密度.[17]
受以上文献的启发,研究者将针对粘性系数依赖于密度的不可压缩流体与多个刚体耦合系统方程的初始密度包含真空情形下局部强解的适定性问题进行探索.该问题的具体数学模型解释如下:
在耦合系统内,流体的运动可以由下列带外力项的粘性依赖于密度的不可压缩Navier-Stokes方程组描述,
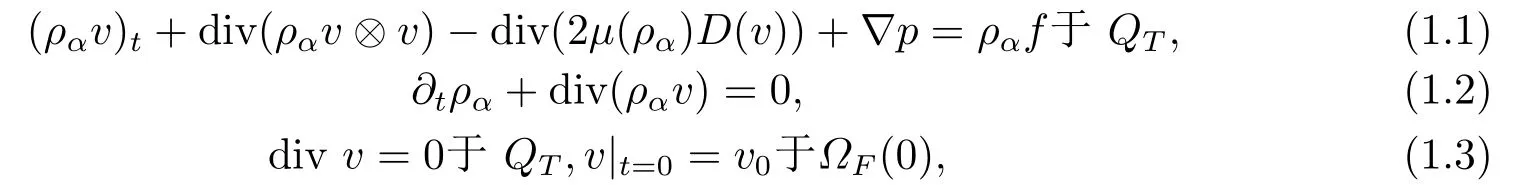
这里(ρα,v,p)分别代表流体密度,速度和压力,µ(ρα)表示依赖于密度的流体粘性系数,流体区域是Ω的一个开子域,即ΩF(t)⊂Ω,QT={(t,x)/t ∈(0,T),x ∈ΩF(t)}为本文所讨论问题的时空空间,其中应变张量Dv=12(∇v+∇Tv),f ∈L2((0,T)×Ω)表示一个固定外力(比如重力),Ωi(t)为t时刻第i个刚体运动的区域(如下图所示).

图1 流固耦合系统示意图
其次,流固耦合系统内的刚体运动遵循牛顿第二定律

以及转动定律

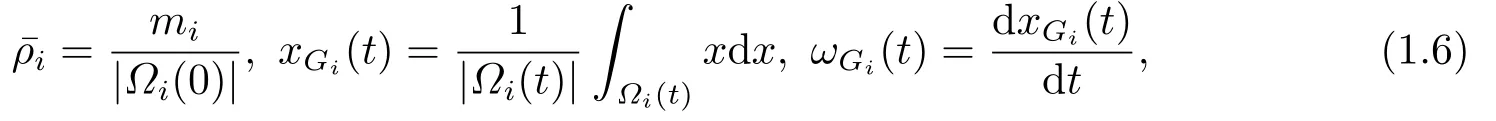

转动惯量Ji遵循

刚体满足初值条件

及Dirichlet边界条件

在流体固体交界处假设无滑动,即有
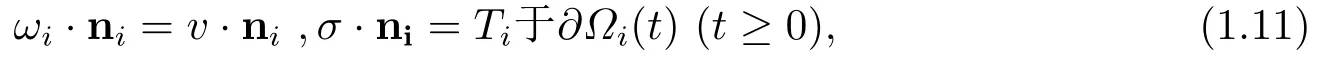
这里−Ti表示第i个刚体对流体的反作用力,用Cauchy应力张量Σi可表示为Ti=Σi·ni.
首先,可通过虚拟区域法将刚体考虑为粘性足够大的流体来进行变量替换


事实上由质量守恒知ρ满足下列线性输运方程[18]

综上,可得整个流固耦合系统的运动方程,即本文主要研究对象

及初边值条件

这里(ΩF(0),Ω1(0),...,Ωs(0))是Ω的开子域.
下面假设

2.主要结果
对于µ为常数的情形,Desjardins[3]得到了二,三维情形下弱解的存在性.本文主要研究的是粘性系数依赖于密度时的系统解的存在性问题,结果如下
定理2.1假设初值(ρ0,u0,f)满足divu0=0,ρi,0D(u0)=0,1is.若满足
1)对某个q ∈(n,+∞)有

2)存在(ρ0,g)∈H1(Ω)×L2(Ω)使得

则存在一个小时刻T∗∈(0,T)及(1.14)-(1.19)的唯一一个强解(ρ,u,p),使得


3.定理的证明
本节假设µ∈C2[0,∞),根据文[10]有下列Stokes方程的经典结果.
引理3.1[10]假设ρ ∈W2,q(Ω),0ρ ≤C,令(u,p)∈H10(Ω)×L2(Ω)是下面边值问题的唯一弱解

则对N=N(n,q)>0,有
1)若F ∈L2(Ω),则(u,p)∈H2(Ω)×H1(Ω),且

2)若F ∈Lr(Ω),r ∈(n,q),则(u,p)∈W2,r(Ω)×W1,r(Ω)且

3)若F ∈H1(Ω),则(u,p)∈H3(Ω)×H2(Ω),且

下面处理线性化系统

这里divv=0.
这是一个线性输运方程和非稳态Stokes方程的非强耦合而成的方程组,其存在性和正则性容易得到,下面来证明非负情况下强解的存在性和正则性结果.
引理3.2假设(ρ0,u0,f)满足定理2.1的假设条件,且有ρ0∈W2,q(Ω),vt ∈L2(0,T;H10(Ω)),divv=0于Ω,v ∈L∞(0,T;H10(Ω)∩H2(Ω))∩L2(0,T;W2,r(Ω))(n 证步1 解空间的构造. 给(3.3)左右两端同时乘以rρr−1可以得到 在(0,t)×Ω上分部积分 化简 即 继续在Ω上分部积分 由于v ∈L∞(0,T;H10(Ω)∩H2(Ω)),可得 借助Gronwall不等式 及Sobolev不等式 可估计不等式右端项得到 正如文[11-19]所证明的,ρ遵循如下正则性估计 接下来使用Garlerkin方法证明强解的存在性. 步2 解的存在性. 首先介绍下列函数空间 这里ϕm为X内Stokes算子A=−P∆的第m个特征函数,P是一个散度为零的投影算子.且∑∞1(ϕ,ϕm)L2ϕm=ϕ于H2(Ω),记(ϕ,ϕm)L2=∫ϕϕmdx. 首先假设ρδ=ρ+δ,0<δ <1,令(uδ0,pδ0)∈H10(Ω)×L2(Ω)解下列边值问题 构造逼近解um ∈C1([0,T];Xm)满足:∀ω ∈Xm有下列方程成立, 这里µδ=µ(ρδ),可以将ω=ϕk(k=1,...,m)代入(3.8)得到具有正则系数的线性常微分方程组.因此,依照线性常微分方程理论[18]容易得到唯一Garlerkin解um的存在性. 步3 一致估计. 由(1.1)及∥ρ(t)∥Lr=∥ρ0∥Lr,(1≤r ≤∞),可知 则易知 即 给(3.3)左右两端同时乘以µ′(ρδ)可得代入上式可得 对(3.12)式在(0,t)积分,而∥µδ∥L∞C,∥ρδ∥L∞C,于是 借助Cauchy不等式可推出 结合以上两个式子,可得 由(3.5)知∥∇ρ∥2L∞C,结合Gronwall不等式可得 接下来对(3.12)关于t求微分,运用线性输运方程(3.3)可以得到 记divumt=0并运用(3.3)有 逐项估计,可知 综上可得 只需估计最后一项,固定τ ∈(0,T),在(τ,T)⊂(0,T)积分, 由Gronwall不等式可推出 接下来取ω=umt=umt(τ)代入(3.8)可以估计最后一项,推出 由不可压缩条件divumt=0,得到 化简得到 因此对(3.17)取τ →0,可以得到如下结论 而当t=0时, 代入(∗)式右端可得 定义 则不等式可写为 由ρδδ及于H2(Ω)可推出 步4 紧性证明. 步3证明结果表明,存在一个序列mk使得于L∞(0,T∗;L2(Ω))且umk ⇀uδt于L2(0,T∗;H1(Ω)).对(3.19)取极限并运用弱∗收敛的下半连续性可知 即存在一序列0<δk <1,当δk →0时有uδk ∗⇀ut于L2(0,T∗;H1),且uδkt ⇀ut于L2(0,T∗;H1(Ω)).又由知 等价于 于是有下列结论 由(3.2)知 综合步1-4的证明过程,最终得到了引理3.2的结论. 下面证明逼近解满足一些一致估计且收敛到原非线性问题(1.14)-(1.18)的一个局部强解. 为了得到此逼近解的一致估计,首先引入一个函数ΦK(t),K1, 下面将逐项估计ΦK,运用Gronwall不等式可最终获得ΦK的局部有界性. 简记µk=µ(ρk)且2Dk(u)=∇uk+∇Tuk.可以观察到δρkC,C−1µkC,|∇µk|C|∇ρk|,|∇2µk|(|∇ρk|2+|∇2ρk|),依赖于∥∂u2/∂ρ2∥C. 对于ΦK的第一项,可以由以下引理得到. 引理3.3存在常数N=N(n,q)>0,使得∀k,1kK有 证在(3.2)两端同时乘以ukt并在Ω分部积分,由Hölder不等式有 记(uk,pk)∈H10(Ω)×L2(Ω)解下列Stokes方程 由Hölder不等式,Sobolev不等式知 由(3.23),(3.24)借助Young不等式,可得存在常数N1=N1(n,q)>0,使得 常数Ni,2i5使得 且 代入到(3.22)可得 对(3.26)关于t积分,可证得该引理. 引理3.4存在常数N=N(n,q)>0,使得∀k,1kK有 其中C0=C(ρ0,u0,p0). 证对几乎处处的t ∈(0,T),ω ∈H10,δ(Ω)={ϕ ∈H10(Ω)|divϕ=0},有 由引理3.2所证明的(ρ,u)的正则性,可得(3.28)右侧被A(t)|ω|H10控制,非负函数A(t)∈L2(0,T).因此可借助文[19]中引理1.1的结果,得到对所有的,(ρut)t ∈L2(0,T;H−1σ(Ω)),这里(Ω)是(Ω)的对偶空间,于是有 即 结合(3.3)并逐项估计(参见文[10])可得, 对(3.29)右侧逐项估计知 其中估计第二项时,利用引理3.1知,存在N7=N7(n,q),使得 取τ ∈(0,T)并对(3.30)在(τ,t)⊂(0,T)积分可得 这里 且 应用Gronwall不等式知 接下来对AK(τ)的估计步骤类似于(3.18),此处简写主要步骤,在(3.3)两端同乘ukt,并借助引理3.1,引理3.2知 因此,在(3.33)中令τ →0可得 即证得该引理. 接下来估计ΦK第二项∥∇ρk∥Lq. 引理3.5存在常数N=N(n,q)>0,使得∀k,1kK有 证由引理3.2 知,对任意n 由ΦK定义知,ΦK1,则,于是由Cauchy不等式知, 引理3.5得证. 现在将(3.27)与(3.35)结合可得对常数N=N(n,q)>0,有 因此可以定义 于是有 由积分不等式及文[9]中关于ΦK估计,易证存在一个依赖于C0及参数C的时间T∗∈(0,T),使得 则得到了ΦK的局部有界性.固定K为足够大的整数,对任意k1,综合上述引理3.3-3.5易得下列一致上界 接下来证明整个序列(ρk,uk)强收敛到原非线性方程(1.14)-(1.18)的一个解.定义σk+1=则有 两式相减,运用方程(3.3)及不可压缩条件divuj=0可得 两侧同时乘以ωk+1,在Ω上积分有 关于时间t微分有 运用Hölder,Sobolev和Cauchy不等式,记可以推出 对上式在Ω积分,并运用(3.6)及ρkδ可知 而由yk+1(0)=0,及Bk(s)∈L1(0,T∗),知 当k=1时,上式显然成立,设k=n时仍然成立,则对于k=n+1时,有 即有 结合(3.38)知 同理 于是可以得到序列(ρk,uk)收敛到L∞(0,T∗;L2(Ω))内的一个极限(ρ,u),对(3.37)关于t积分可得在L2(0,T∗;H10(Ω))内uk →u. 从以上收敛过程,可以得到(ρ,u)为(1.14)-(1.16)的一个弱解(详见文[20]).利用文[20]中散度自由向量场的经典结论可得(3.36)满足如下的一致估计 即 至此完成了在初始密度非负ρ0δ >0,µ∈C2假设下的强解的存在性证明.[21] 下面证明一般情形下的存在性.令(ρ0,u0)满足定理2.1的假设条件,则对于任意δ ∈(0,1),取ρδ0∈W2,q(Ω)及µδ ∈C2[0,∞),能使得当δ →0时,有 记(uδ0,pδ0)∈{H10(Ω)×L2(Ω)}是下列方程的一个解 则相应的解(ρ0,u0,p0)满足(4.1),C0=C(ρ0,u0,p0)=∥g∥2L2.而由于∥µδ −µ∥C1→0,所以C不依赖于δ.取在弱意义下收敛到(ρ,u,p)的序列(ρδ0,uδ0,pδ0),显然为满足正则性估计(4.1)的原非线性问题的一个强解.由Lions[21]易得该解唯一性的证明,连续性的证明类似于文[10],这里从简. 主要利用(3.36)与质量守恒方程得到ρt的存在区间,结合紧性结论得到ρ的右连续.固定t0∈[0,T∗],知 此外,对(3.25)在[τ,t)上积分可以得到,对N=N(n,q)>0,有 由(3.24)可知 由(3.31)知 对(3.32)式运用积分形式的Gronwall不等式知 由(3.5)知 运用微分形式的Gronwall不等式,结合以上估计可以得到如下的爆破准则 即t →T∗时,有J(t)→∞.所以我们要求T∗足够小.至此,我们证明了定理2.1的全部结论.






















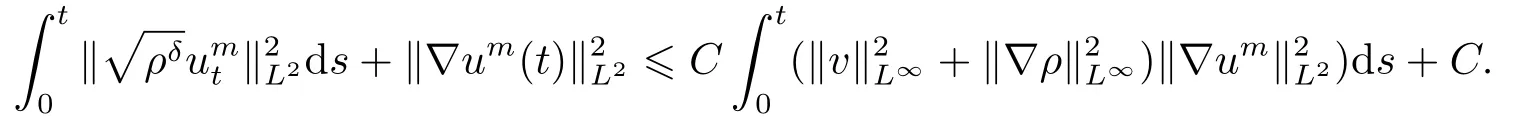






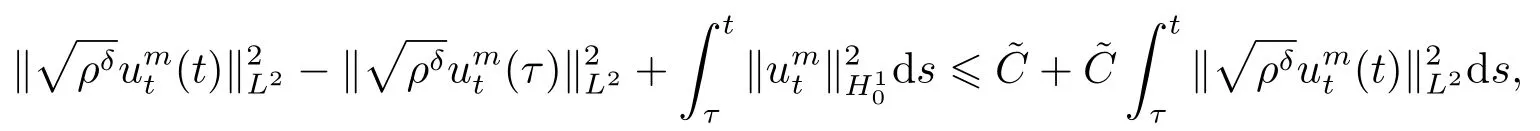
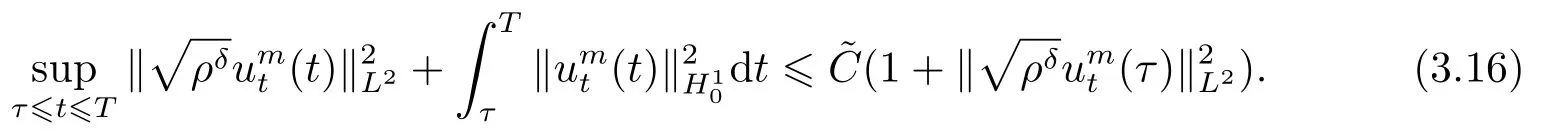

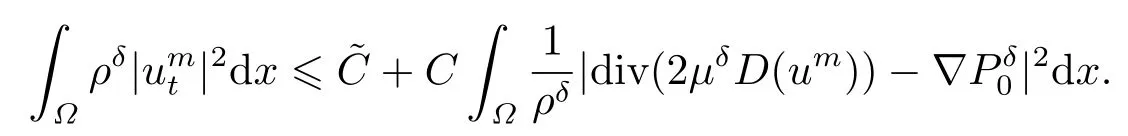


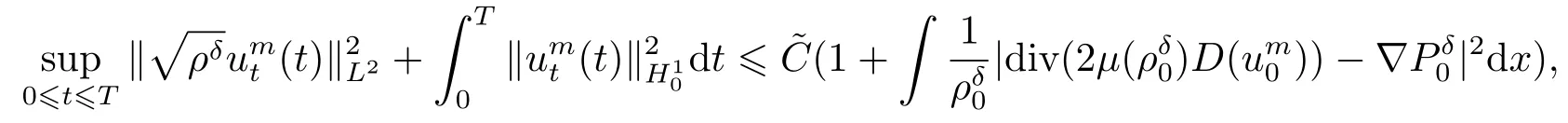





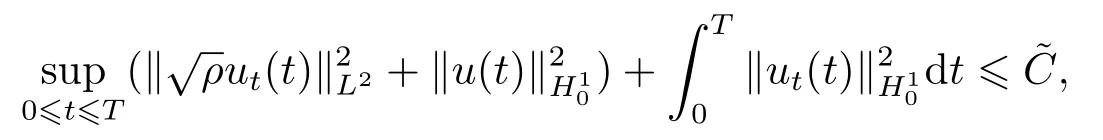





























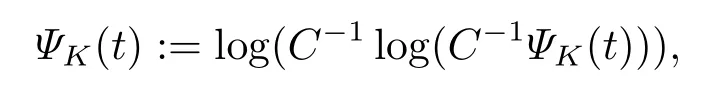
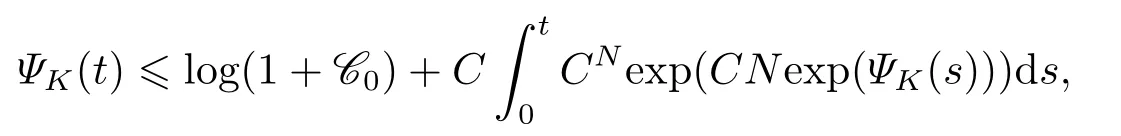
















4.总结