半群PTn(A;θ)的正则性及格林关系

秦美青

(菏泽学院 数学与统计学院,山东 菏泽 274015)

1951年J.A.Green在文献[1]中提出了半群S上的5种等价关系L,R,J,H,D的概念并进行研究,后来这5种等价关系被统称为半群S上的Green’s关系.格林关系在半群的代数理论的形成和发展中起着非常重要的作用,对于揭示半群的代数结构有着重要的意义,多年来是半群的代数理论研究的热点课题之一[2—8].

设X是一个非空集合,T(X)是X上的完全变换做成的半群.设A是X的非空子集,文献[2]讨论了T(X)的子半群T(X,A)={α∈T(X):imα⊆A}的自同构问题.文献[3]探究了半群T(X,A)上的正则性及元素间的格林关系.

取定θ∈PTn(A)且设domθ=Xn.定义半群PTn(A)上的一个新的运算∘:f∘g=fθg,其中f,g∈PTn(A),乘积fθg为部分变换f,θ,g在通常意义下的合成.这样,在运算∘下,PTn(A)构成一个新的半群,称为半群PTn(A)的变种半群,记为PTn(A;θ).显然半群PTn(A)可视为半群PTn(A;θ)的一种特殊情形(当θ为Xn上的恒等变换时PTn(A;θ)=PTn(A)).

1975年,Magill和Subbiah在文献[5]中探讨了一般变种半群上正则元的特征及正则元之间的格林关系.此后对变种半群的研究不断深入,得到了许多丰富的结果.如文献[6]在集合X(|X|≥3),PX是X上的部分变换半群,E是X上的等价关系的条件下,考察了PX由等价关系E确定的保等价关系的子半群

PE(X)={f∈PX:∀x,y∈domf,(x,y)∈

E⟹(f(x),f(y))∈E}

的正则性及任意元素间的格林关系.文献[7]刻画了半群PE(X)的变种半群PE(X;θ)的正则元,给出了半群PE(X;θ)为正则半群的充要条件.文献[8]刻画了半群PE(X;θ)上任意元素间的格林关系.设X是非空集合,TX是X上的完全变换半群,对于X上的非平凡等价关系E,文献[9]考察了保等价关系变换半群

TE(X)={f∈TX:(x,y)∈E⟹(f(x),f(y))∈E}

的变种半群TE(X;θ)上的自然偏序关系.给出了半群TE(X;θ)上偏序关系的定义,考察了半群中两个元素何时存在此偏序关系,并探讨了关于此偏序关系相容的元素.

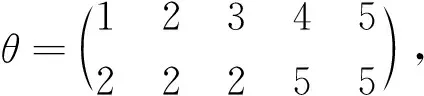
下文中未说明的概念与符号请参考文献[10—12].

1 正则性

E(PTn(A;θ))表示半群PTn(A;θ)中幂等元做成的集合.

定义1[1]设S是半群,对于S中每个元素a,若存在元素b∈S,使得aba=a,则称a是S的正则元.若S中每个元素都是正则元,则称S是正则半群.

定义2[13]设f∈PX和x∈imf,集合{y∈domf:(y)f=x}记为(x)f-1.

定义3[13]设f∈PX,集合{(x)f-1:x∈imf}记为π(f).

引理1[4]半群PTn(A)是正则半群的充要条件为|A|=1或A=Xn.

引理2[4]半群PTn(A)中所有正则元组成的集合RPTn(A)={α∈PTn(A):imα=((Dα(A))α}为半群PTn(A)的右理想(其中Dα(A)=A∩domα).

定理1设f∈PTn(A;θ),则f∈E(PTn(A;θ))当且仅当对每个y∈imf⊆A,有yθ∈(y)f-1.

证明必要性.任取y∈imf⊆A,则存在x∈domf,使得y=(x)f.因为f是幂等元,所以y=(x)f=(x)f∘f=(x)fθf=(yθ)f.从而yθ∈(y)f-1.

充分性.任取y∈imf⊆A,则存在x∈domf,使得y=(x)f.因为yθ∈(y)f-1,所以y=(yθ)f,从而有(x)f=y=(yθ)f=((x)f)θf=(x)f∘f,即f=f∘f,从而f是幂等元.

定理2设f∈PTn(A;θ),则f∈R(PTn(A;θ))当且仅当对每个y∈imf有(y)f-1∩Aθ≠Ø且(θ|imf是单射(其中R(PTn(A;θ))表示PTn(A;θ)中所有正则元构成的集合).

证明必要性.任取y∈imf⊆A,则存在x∈domf,使得y=(x)f.因为f∈R(PTn(A;θ)),所以存在g∈PTn(A;θ),使得f=f∘g∘f,这样

y=(x)f=(x)f∘g∘f=(xfθg)θf,

从而(xfθg)θ∈(y)f-1,显然(xfθg)θ∈Aθ,从而(y)f-1∩Aθ≠Ø.

任取y1,y2∈imf且y1≠y2,则存在x1,x2∈domf,使得y1=(x1)f,y2=(x2)f.若y1θ=y2θ,则

y1=(x1)f=(x1)f∘g∘f=

(x1)fθgθf=(y1θ)gθf=(y2θ)gθf=

(x2)fθgθf=(x2)f=y2.

这与y1≠y2矛盾,从而(θ|imf是单射.

充分性.记imf={y1,y2,…,yt}.因为对每个yi∈imf,有(yi)f-1∩Aθ≠Ø,所以存在a∈A,使得aθ∈(yi)f-1.取定ai∈{a∈A,aθ∈(yi)f-1}.定义g如下:domg=A.对任意a∈A,若a=yiθ,i=1,2,…,t-1,则令(a)g=ai.否则,令(a)g=at.因为(θ|imf是单射,所以g是良定义的.对任意x∈domf,存在yi∈imf,使得(x)f=yi,则有

(x)f∘g∘f=(x)fθgθf=

(yiθ)gθf=(aiθ)f=yi=(x)f,

即f=f∘g∘f,从而f是正则元.

定理3半群PTn(A;θ)是正则半群当且仅当以下条件成立:

(ⅰ)θ|A:A→Aθ为双射;

(ⅱ)A=Xn或|A|=1.

证明必要性.任取f∈PTn(A;θ).由半群PTn(A;θ)是正则半群知,存在g∈PTn(A;θ),使得f=f∘g∘f=f(θgθ)f,从而f是PTn(A)中的正则元,故PTn(A)是正则半群,由引理1知条件(ⅱ)成立.1A∈PTn(A;θ)且是正则元,根据定理2知(θ|A是单射,显然是满射,从而(θ|A是双射.

充分性.若|A|=1,则对任意f∈PTn(A;θ),f是幂等元,显然是正则元.

2 格林关系

定义4[14]设A,B是X的两个子集簇.若对每个A′∈A,都存在B′∈B,使得A′⊆B′,则称A是B的细化.

引理3[3]设S为半群,a,b∈S,则

(ⅰ)aLb当且仅当存在x,y∈S1,使得a=xb,b=ya,

(ⅱ)aRb当且仅当存在x,y∈S1,使得a=bx,b=ay,

(ⅲ)aJb当且仅当存在x,y,u,v∈S1,使得a=xby,b=uav,

(ⅳ)H=L∩R,D=L∘R.

定理4设f,g∈PTn(A;θ),则(f,g)∈L当且仅当f=g或

imf=(A∩domθg)θg=(A∩domθf)θf=img.

证明必要性.由(f,g)∈L知存在h,k∈PTn(A;θ),使得f=h∘g=hθg,g=k∘f=kθf.这样

imf=imhθg⊆(A∩domθg)θg⊆

img=imkθf⊆(A∩domθf)θf⊆imf,

从而imf=(A∩domθg)θg=(A∩domθf)θf=img.

充分性.由imf=(A∩domθg)θg知,对任意y∈imf,存在x∈A∩domθg⊆A,使得y=(x)θg.取定xy∈{x∈A∩domθg:y=(x)θg}.构造h如下:令domh=domf,对任意z∈domh,(z)h=x(z)f,显然h∈PTn(A;θ)且对任意的z∈domh,(z)hθg=(x(z)f)θg=(z)f,即f=hθg=h∘g.同理可构造k∈PTn(A;θ),使得g=k∘f,从而(f,g)∈L.

定理5设f∈PTn(A;θ),则(θ|imf是单射当且仅当π(f)=π(fθ).

证明必要性.任取y∈imfθ,则存在x1,x2∈(y)(fθ)-1⊆π(fθ),使得(x1)fθ=y=(x2)fθ.因为(θ|imf是单射,所以(x1)f=(x2)f,即存在z∈imf,使得x1,x2∈(z)f-1∈π(f),从而π(fθ)加细π(f).显然π(f)加细π(fθ),故π(f)=π(fθ).

充分性.任取y1,y2∈imf且设y1≠y2,则存在x1,x2∈domf,使得y1=(x1)f,y2=(x2)f.若y1θ=y2θ,即(x1)fθ=(x2)fθ,则存在y∈imfθ,使得x1,x2∈(y)(fθ)-1⊆π(fθ)=π(f),故存在z∈imf,使得x1,x2∈(z)f-1,即y1=(x1)f=z=(x2)f=y2,这与y1≠y2矛盾,故(θ|imf是单射.

定理6设f,g∈PTn(A;θ),则(f,g)∈R当且仅当f=g或(θ|imf,(θ|img都是单射且π(f)=π(g).

证明必要性.由(f,g)∈R知存在h,k∈PTn(A;θ),使得f=g∘h=gθh,g=f∘k=fθk,这样

domf=dom(gθh)=

(img∩dom(θh))g-1⊆domg=dom(fθk)=

(imf∩dom(θk))f-1⊆domf,

从而domf=domg.任取y∈imf⊆A,设x1,x2∈(y)f-1∈π(f),即(x1)f=y=(x2)f,这样

(x1)g=(x1)fθk=(x2)fθk=(x2)g,

从而存在z∈img⊆A,使得x1,x2∈(z)g-1∈π(g),故π(f)是π(g)的细化.类似可证π(g)是π(f)的细化,从而有π(g)=π(f).

任取y1,y2∈imf⊆A且y1≠y2,则存在x1,x2∈domf=domg,使得y1=(x1)f,y2=(x2)f.若y1θ=y2θ,即(x1)fθ=(x2)fθ,这样(x1)g=(x1)fθk=(x2)fθk=(x2)g,从而存在z∈img,使得x1,x2∈(z)g-1∈π(g)=π(f),故存在y0∈imf,使得x1,x2∈(y0)f-1,即y1=(x1)f=y0=(x2)f=y2,这与y1≠y2矛盾,从而y1θ≠y2θ,故(θ|imf是单射.类似可证(θ|img是单射.

充分性.(θ|imf,(θ|img都是单射且π(f)=π(g).需要构造h,k∈PTn(A;θ),使得f=g∘h,g=f∘k.取定x0∈im(gθ)⊆A.定义h如下:令domh=A,

显然h是良定义的且h∈PTn(A;θ).由

π(f)=π(g)可知domf=domg.

dom(g∘h)=dom(gθh)=

(img∩dom(θh))g-1=

[img∩(imθ∩domh)θ-1]g-1=

[img∩(imθ)θ-1]g-1=domg=domf.

对任意x∈dom(gθh),

(x)g∘h=(x)gθh=((x)gθ)h=

(((x)gθ)(gθ)-1)f=(x)f.

因此f=g∘h.

类似可证存在k∈PTn(A;θ),使得g=f∘k,从而有(f,g)∈R.

定理7设f,g∈PTn(A;θ),则(f,g)∈H当且仅当f=g或

imf=(A∩domθg)θg=

(A∩domθf)θf=img,

π(f)=π(g)且(θ|imf,(θ|img都是单射.

定理8设f,g∈PTn(A;θ),则(f,g)∈D当且仅当f=g或(θ|imf,(θ|img都是单射且

|imf|=|(A∩domθg)θg|=

|(A∩domθf)θf|=|img|.

证明必要性.因为(f,g)∈D,则存在h∈PTn(A;θ),使得fLh,hRg.由fLh知

imf=(A∩domθh)θh=(A∩domθf)θf=imh.再由hRg知(θ|imh,(θ|img都是单射且π(g)=π(h).因为imf=imh,所以(θ|imf也是单射.根据π(g)=π(h)与imf=(A∩domθh)θh知|imf|=|img|=|(A∩domθg)θg|,从而有

|imf|=|(A∩domθf)θf|=

|(A∩domθg)θg|=|img|.

|imf|=|(A∩domθf)θf|=

|(A∩domθg)θg|=|img|=

|imh|=|(A∩domθh)θh|

得imf=(A∩domθf)θf=(A∩domθh)θh=imh,从而fLh,综上知(f,g)∈D.

定理9设f,g∈PTn(A;θ),若对某个h∈PTn(A;θ),k∈PTn(A;θ)1,有f=h∘g∘k,则|imf|≤|(A∩domθg)θg|.

证明已知f=h∘g∘k,其中h∈PTn(A;θ),k∈PTn(A;θ)1.若k=1,则f=h∘g,imf=im(h∘g)=im(hθg)⊆(A∩domθg)θg,从而有|imf|=|im(h∘g)|≤|(A∩domθg)θg|.若k∈PTn(A;θ),则

|imf|=|im(h∘g∘f)|≤

|im(h∘g)|≤|(A∩domθg)θg|.

综上可知,若f=h∘g∘k,其中h∈PTn(A;θ),k∈PTn(A;θ)1,则一定有

|imf|≤|(A∩domθg)θg|.

定理10设f,g∈PTn(A;θ)且f≠g,则(f,g)∈J当且仅当π(f)=π(g)且(θ|imf,(θ|img都是单射或

|imf|=|(A∩domθf)θf|=

|(A∩domθg)θg|=|img|.

证明必要性.设fJg,则存在h,k,h′,k′∈PTn(A;θ)1,使f=h∘g∘k,g=h′∘f∘k′.若h=1=h′,则f=g∘k,g=f∘k′,从而fRg,故π(f)=π(g)且(θ|imf,(θ|img都是单射.

若h∈PTn(A;θ)或h′∈PTn(A;θ),则一定可找到s,s′∈PTn(A;θ),t,t′∈PTn(A;θ)1,使得f=s∘g∘t,g=s′∘f∘t′.不妨以h=1且h′∈PTn(A;θ)为例,当h=1时,f=g∘k,g=h′∘f∘k′,从而f=g∘k=h′∘f∘k′∘k=h′∘g∘k∘k′∘k=h′∘g∘(k∘k′∘k),由定理9得

|(A∩domθg)θg|≥|imf|≥

|(A∩domθf)θf|≥|img|≥

|(A∩domθg)θg|,

从而有

|imf|=|(A∩domθf)θf|=

|(A∩domθg)θg|=|img|.

充分性.π(f)=π(g)且(θ|imf,(θ|img都是单射,fRg,从而fJg.若

|imf|=|(A∩domθf)θf|=

|(A∩domθg)θg|=|img|,

则定义γ,λ如下:令π(f)=π(γ),

imγ=(A∩domθg)θg⊆img,π(λ)=π(g),

imλ=(A∩domθf)θf⊆imf,

类似可证存在f′∈PTn(A;θ),使得λ=f′∘f,从而f=g′∘g∘γ′,g=f′∘f∘λ′,故fJg.