n维m阶强预不变凸模糊数值函数的性质

白玉娟, 刘 坤, 张 琛

(陇东学院 数学与统计学院,甘肃 庆阳 745000)

众所周知,凸性理论在对策论、工程、管理科学和最优化理论中起着非常重要的作用.然而,许多实际问题形成的数学模型,常常不能满足凸规划的基本要求,于是研究各种各样的广义凸性以及与数学规划问题相关联的一些基本性质非常必要.1981年,Hanson在文献[1]中提出了不变凸函数的定义并将其推广为拟不变凸和伪不变凸.1988年,T. Weir和B. Mond在文献[2]中提出预不变凸函数的定义,并研究了此类函数在最优化中的应用.2001年,杨新民在文献[3]中又给出了预不变凸函数的其他性质.随后颜丽佳在文献[4]中又提出了强预不变凸函数.唐万梅、彭再云在文献[5—6]中研究了强预不变凸函数的性质.但在具体的优化问题数学建模过程中往往需要模糊数描述不确定参数,因此,关于模糊凸分析理论与其相对应的模糊优化问题的研究,引起了广大学者的兴趣.1994年,M. A. NOOR在文献[7]中给出了预不变凸模糊映射和模糊不变凸集的概念.1999年,Y. R. SYAU在文献[8]中定义了η为向量值函数的预不变凸性,得到预不变凸模糊映射的2个刻画定理,并讨论了其在优化理论中的应用.2016年,巩增泰利用Goetschel和Voxman在文献[9]所定义的模糊数之间的一种序关系在文献[10—11]中定义了高维模糊数空间上的偏序关系,并对n维模糊映射的凸性、可微性与相应的凸优化理论进行了系统的研究.随后讨论了预不变凸、严格预不变凸、若严格预不变凸、预拟不变凸、严格预拟不变凸、若严格预拟不变凸的性质及其相互关系.基于对n维模糊映射预不变凸性的进一步研究,结合蔡威在文献[12]中对高阶强预不变凸函数的刻画,作为文献[10—11]的延续和广义凸性的研究,本文首先给出了n维m阶强预不变凸模糊数值函数的定义,其次在某种序意义下讨论了n维m阶强预不变凸模糊数值函数的若干性质.

1 预备知识

定义1[13]设u∈F(Rn),若u满足以下性质:

(ⅰ)u是一个正规模糊集,即存在x0∈Rn使得u(x0)=1,

(ⅱ)u是一个凸模糊集,即对∀x,y∈Rn,λ∈[0,1],u(λx+(1-λ)y)≥min{u(x),u(y)},

(ⅲ)u是上半连续函数,即[u]r={x∈Rn:u(x)≥r}是闭集,其中r∈(0,1],

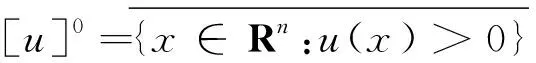
则称u为n维模糊数构成的n维模糊数空间,记为En.

当r=1时,称[u]1={x∈Rn:u(x)=1}为模糊数u的核.

定理1(n维模糊数表示定理)[14]设u∈En,则

(ⅰ)对任意r∈(0,1],[u]r均为Rn上的非空紧凸集,

(ⅱ)若0≤r1≤r2≤1,则[u]r2⊂[u]r1,

(ⅲ)若正数列rn非降收敛于r∈(0,1],则

模糊数的加法和数乘运算定义如下:设u,v∈En,k,k1,k2∈R则

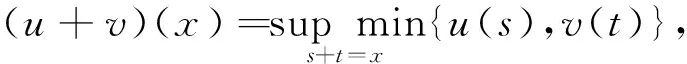
k(u+v)=ku+kv,

[u+v]r=[u]r+[v]r=

{x+y:x∈[u]r,y∈[v]r}，

[ku]r=k[u]r={kx:x∈[u]r}.

定义2[9]设u,v∈E,u⪯v是指

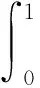
其中

[u]r=[u-(r),u+(r)],

[v]r=[v-(r),v+(r)],r∈[0,1].

定义3[10]设u∈F(Rn),对任意r∈[0,1],称

定义4[10]设u∈En,称向量值函数τ:En→Rn,

为模糊数空间En上的一个序值函数,其中

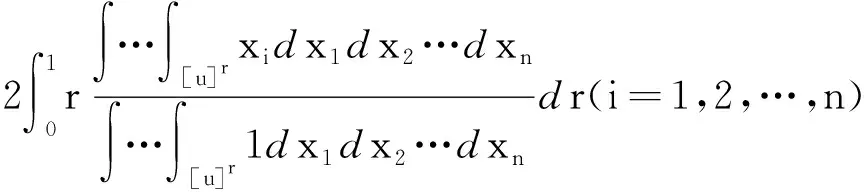
定义5设u,v∈En,C⊆Rn是满足0∈C且C≠Rn的一个闭凸锥,若τ(u)∈τ(v)+C,则称v优于u,记为u⪯cv.

若u,v∈E,C=[0,+∞),则定义5与定义2一致.

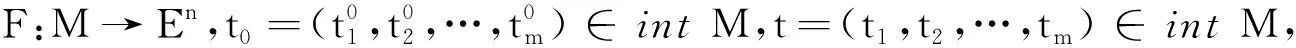
则称F在t0处可微,称模糊向量{u1,u2,…,um}为F在t0处的梯度,记作F(t0)={u1,u2,…,um}.

定义7[2]设集合M(⊂Rn),若存在一个向量函数η:Rn×Rn→Rn,使得对∀t,t′∈M,∀λ∈[0,1]满足t′+λη(t,t′)∈M,则称集合M(⊂Rn)是不变凸集.

若∀t,t′∈M,∀λ∈[0,1]满足η(t,t′)+η(t′,t)=0,则称η:Rn×Rn→Rn为非对称映射.特别地,η(t,t′)=t-t′时M退化为一般凸集.

条件C1[15]设M(⊂Rn)是关于向量函数η:Rn×Rn→Rn的非空不变凸集,称η满足条件C1是指η对任意的t,t′∈M,λ∈[0,1]都满足以下条件:

(ⅰ)η(t′,t′+λη(t,t′))=-λη(t,t′),

(ⅱ)η(t,t′+λη(t,t′))=(1-λ)η(t,t′).

若η满足条件C1,∀λ1,λ2∈[0,1],则

η(t′+λ1η(t,t′),t′+λ2η(t,t′))=

(λ1-λ2)η(t,t′).

2 n维强预不变凸模糊映射的性质

定义8设M(⊂Rn)是关于η:Rn×Rn→Rn的非空不变凸集,F:M→En为定义在M上关于η的n维模糊数值函数.

(Ⅰ)若存在β>0,对∀t,t′∈M,∀λ∈[0,1],有

F(t′+λη(t,t′))⪯c

则称F是m阶强预不变凸模糊数值函数.

若β=0,则称F是预不变凸模糊数值函数.

若m=2,则称F是强预不变凸模糊数值函数.

若m=2,η(t,t′)=t-t′,则称F是强凸模糊数值函数.

若m>2,η(t,t′)=t-t′,则称F是m阶强凸模糊数值函数.

(Ⅱ) 若存在β>0,对∀t,t′∈M,∀λ∈[0,1],有

则称F是m阶强不变凸模糊数值函数.

(Ⅲ)若存在β>0,对∀t,t′∈H,H(⊂Rn)是凸集,∀λ∈[0,1],有

F(λt+(1-λ)t′))⪯c

则称F是m阶强拟凸模糊数值函数.

(Ⅳ)若存在β>0,对∀t,t′∈H,H(⊂Rn)是凸集,∀λ∈[0,1],有

F(λt+(1-λ)t′))⪯c

则称F是m阶强凸模糊数值函数.

定理2设M(⊂Rn)是关于η:Rn×Rn→Rn的非空不变凸集,两个模糊数值函数kF:M→En和lG:M→En是m阶强预不变凸的,其中k,l是任意常数,则kF+lG也是m阶强预不变凸的.

证明因为kF和lG是m阶强预不变凸的,k,l是任意常数,故存在常数β1>0,β2>0使∀t,t′∈M,∀λ∈[0,1],有

kF(t′+αη(t,t′))⪯c

lG(t′+αη(t,t′))⪯c

所以

(kF+lG)(t′+αη(t,t′))=

kF(t′+αη(t,t′))+lG(t′+αη(t,t′))⪯c

α[kF(t)+lG(t)]+(1-α)[kF(t′)+lG(t′)]-

α(kF+lG)(t)+(1-α)(kF+lG)(t′)-

故kF+lG也是m阶强预不变凸的.

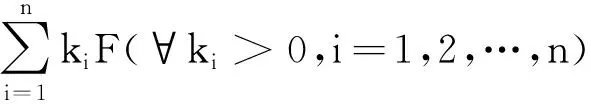
定理4设M(⊂Rn)是非空不变凸集,若F:M→En在M上是m阶强预不变凸的且在M上可微,则F是m阶强不变凸的.

证明F:M→En在M上是m阶强预不变凸的,故存在常数β>0,使得对∀t,t′∈M和满足

F(t′+λη(t,t′))⪯c

又F在M上可微,从而

F(t′+λη(t,t′))=

F(t′)+λη(t,t′)TF(t′)+ο(λ),

故

F(t′)+λη(t,t′)TF(t′)+ο(λ)⪯c

两边同除以λ,有

再令λ→0得

所以F是m阶强不变凸的.

定理5设M(⊂Rn)是关于η:Rn×Rn→Rn的非空不变凸集,向量函数η满足条件C1,且对∀t,t′∈M,当t≠t′时η(t,t′)≠0.若F:M→En在M上是m阶强预不变凸的,则对∀t,t′∈M,t≠t′,函数φ(α)=F(t′+αη(t,t′))在[0,1]上是m阶强拟凸的.

证明设F是M上m阶强预不变凸的,则存在常数β>0使得对∀t,t′∈M,∀α∈[0,1]有

F(t′+αη(t,t′))⪯c

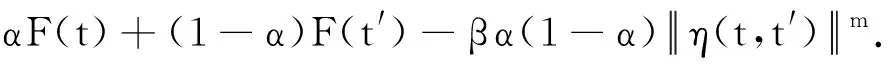
(1)

对∀μ1,μ2∈[0,1],∀α∈[0,1],若μ1=μ2,则

φ(αμ1+(1-α)μ2)=φ(μ2)=

F(t′+μ2η(t,t′))=

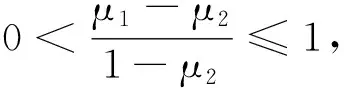
φ(αμ1+(1-α)μ2)=

F(t′+(μ2+α(μ1-μ2))η(t,t′))=

F(t′+μ2η(t,t′)+α(μ1-μ2)η(t,t′)).

(2)

由条件C1可得

η(t′+μ1η(t,t′),t′+μ2η(t,t′))=

η(t′+μ2η(t,t′)+(μ1-μ2)η(t,t′),

t′+μ2η(t,t′))=η(t′+μ2η(t,t′)+

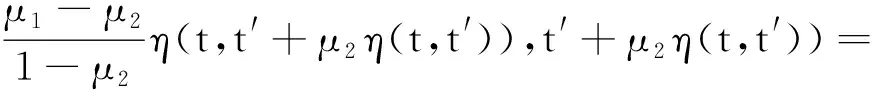
(3)

由(1)～(3)式得

φ(αμ1+(1-α)μ2)=

F(t′+(μ2+α(μ1-μ2))η(t,t′))=

F(t′+μ2η(t,t′)+

αη(t′+μ1η(t,t′),t′+μ2η(t,t′)))⪯c

αF(t′+μ1η(t,t′))+

(1-α)F(t′+μ2η(t,t′))-βα(1-α),

αφ(μ1)+(1-α)φ(μ2)-

αφ(μ1)+(1-α)φ(μ2)-

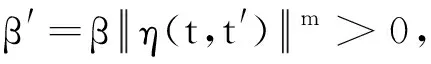
定理6设M(⊂Rn)是关于η:Rn×Rn→Rn的非空不变凸集,向量函数η满足条件C1,且对∀t,t′∈M,当t≠t′时η(t,t′)≠0.若F:M→En在M上是m阶强预不变凸的,则对∀t,t′∈M,t≠t′,函数φ(α)=F(t′+αη(t,t′))在[0,1]上是m阶强凸的.

由定义8及定理5易证定理6.