侧门防撞杆静态挤压强度优化研究

胡浩 夏丁 吕丽文 罗勇 郭伟春

（东风汽车有限公司东风日产乘用车公司技术中心）

车门静态抗压性能是车门被动安全的重要性能之一，同时与侧碰性能具备强关联性，在国家法规中有明确的规定。而车门防撞杆作为车门重要承力结构部品，其静压性能对车门的静压性能有至关重要的影响。近年来随着材料和制造技术的发展，车门防撞杆出现了多种形式。但随着乘用车油耗的限制越发严格，轻量化已成为车门设计的重要课题。车门防撞杆的重量增加同时也会进一步恶化车门下沉等性能。因此车门防撞杆的设计需要综合考虑各种因素。关于车门防撞杆性能的研究，已有学者做过相关研究。文献[1]研究了车门车门下沉和侧碰的防撞杆优化。文献[2]进行了车门静压的强度分析。文献[3]进行了高强钢组织性能对防撞杆静压性能的分析。文献[4]对M型防撞杆进行了静压性能研究。文献[5]研究了热冲压防撞杆材料性能梯度的优化。文章针对圆形钢管，AL挤压型材以及热成形高强钢，3种形式防撞杆进行了对比。同时，针对M型热成形高强钢防撞杆提出了压溃区域局部封闭补强的优化方案。针对断面参数和补强方案，进行了以重量和平均反力为多目标的设计优化。

1 车门静压

1.1 法规要求

车门静压试验操作方法在GB/T 15743—1995中有明确的法规要求。在试验中，如图1所示，要求加载工装在152 mm行程范围内，其平均抵抗反力大于10 kN。图2示出某车型静态挤压试验。

图2 车门静态挤压试验

1.2 防撞杆单品静压试验

防撞杆作为车门重要的承力部品，在其的开发过程中，也需要进行静压试验。防撞杆总成在静压时两端固定，取车门静压位置设置压头，压头以小于12.7 mm/s的速度向下运动，记录压头的行程和压力，如图3、图4所示。

图3 防撞杆静压试验示意图

图4 防撞杆静压试验

1.3 F-S曲线

将车门静压试验和与防撞杆静压试验位移与反力试验结果整理到F-S曲线中。车门在152 mm行程内平均反力为12.11 kN，防撞杆在152 mm行程内平均反力为11.40 kN，防撞杆占比达到90%以上。因此，防撞杆的设计和反力对于车门静压有至关重要的影响。

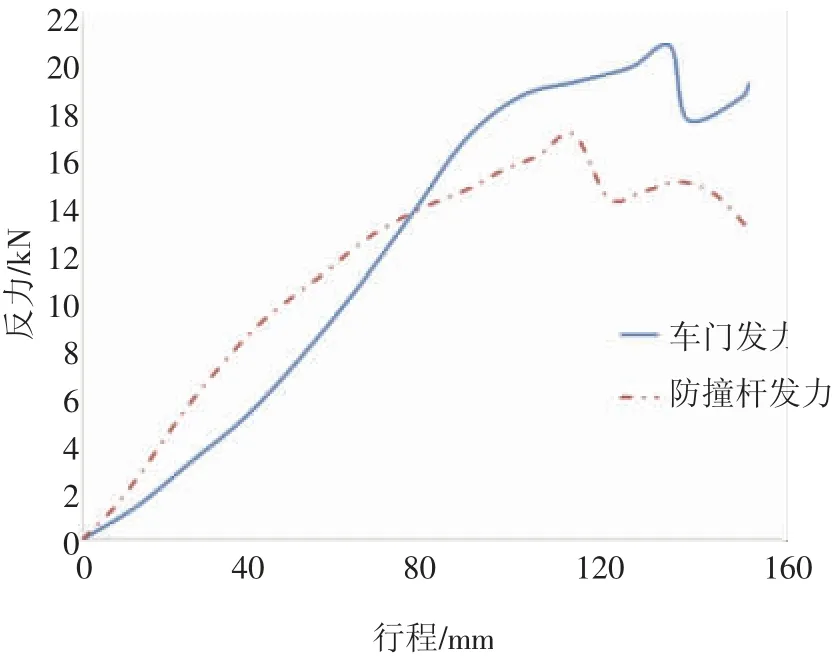
图5 车门与防撞杆F-S曲线

2 不同类型防撞杆比较

目前小轿车车门防撞杆主要有：钢管式、铝挤出型材式、M型热成形高强钢式等形式，为各大汽车厂商广泛使用。

2.1 不同形式防撞杆对比

针对3种主要的防撞杆形式，从断面，工艺，布置以及成本方面进行对比，如表1所示。

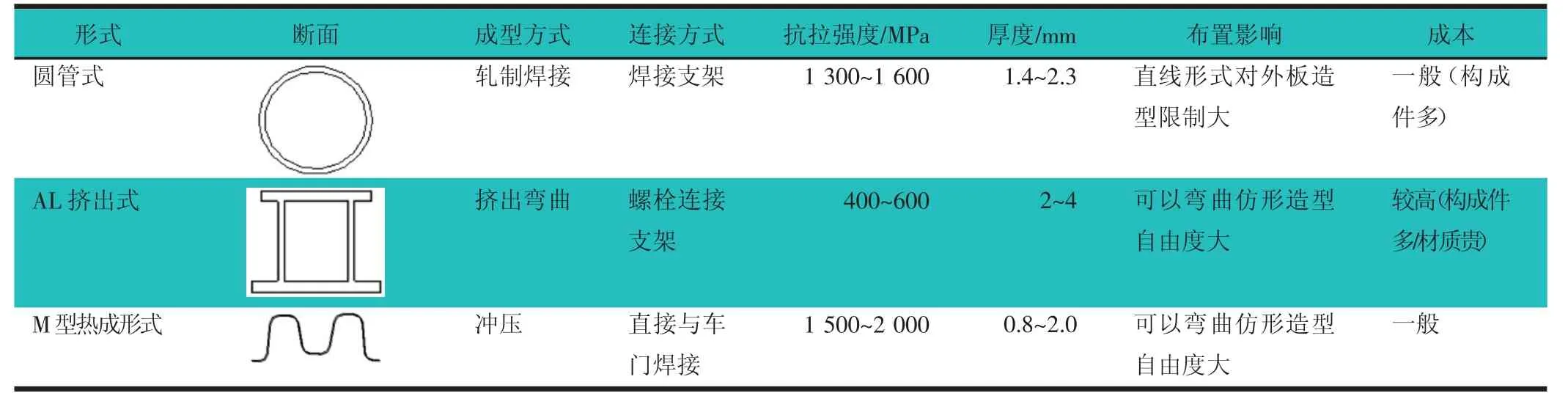
表1 不同形式防撞杆比较

近年来随着热成形技术的发展，以及车门造型要求的提升，可以与车门外板随形的M型热成形防撞杆的应用已越来越广泛。

2.2 防撞杆静压等效3点弯曲试验

如今汽车市场竞争激烈，成本控制越发严格，考虑选取成本较低的钢管型和M型热成形型式两种形式防撞杆进行静态挤压强度的对比。目前考察不同截面形式防撞杆静压性能，主要通过3点弯曲试验进行对比，如图6所示。

针对钢管式和M型热成形式防撞杆我们选择同样的加载条件，进行实物的压弯试验。试验后的样件及F-S曲线，如图7所示。

图7 2种形式防撞杆反力

针对2种形式防撞杆试验及结果进行对比，如表2所示。数据显示M型热成形式相对钢管式，其质量减轻4.8%，反力提升2.9%。

表2 钢管型和M型试验对比

综上，在同等质量情况下，M型热成形防撞杆可以通过截面设计得到更好的反力性能。同时，M型热成形防撞杆具备弯曲随形的优点，可以支撑更好的车门外观造型自由度。

3 M型热成形防撞杆局部加强

上文试验结果显示，M型热成形防撞杆在压弯过程中，反力达到最大值之后迅速下降，因此如何提升防撞杆反力，应从增强截面稳定性和延缓压溃方面进行研究。

3.1 防撞杆弯曲理论

防撞杆静态挤压试验可以简化为梁的弯曲受力，如图8所示。

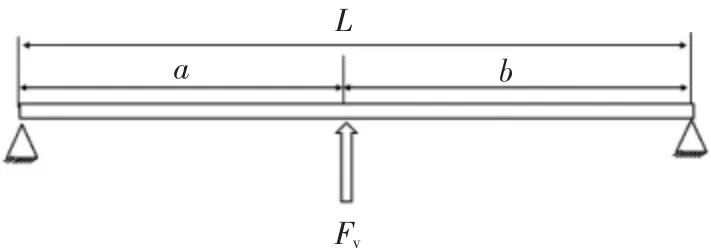
图8 防撞杆静压受力图

根据工程力学梁弯曲分析，受力点处截面弯矩最大为：

由于材料在达到抗拉极限后会出现开裂颈缩，零件的反力从而快速的下降，由弯曲变形截面的受力分析：

当材料达到抗拉极限时，反力：

3.2 局部加强方案及CAE建模

根据式（3）可知，应力集中区域为压弯受力点截面处。如需提高反力，可以针对该区域提高截面的抗弯系数，这样可以使整个杆件的应力分布更加均匀，延缓开裂，提升反力。

文章提出了针对M型热成形防撞杆进行压溃区域局部补强的方案。在M型防撞杆背部，以静压加载点为中心对称分布，焊接一块拉伸强度980 MPa的钢板，如图9所示。

图9 M型防撞杆局部加强方案

针对3点弯曲试验进行CAE建模，分析局部加强前后的变形及平均反力情况。如图10所示为局部补强前后CAE的变形及应力分布结果，结果表明局部补强后应力的分布相对局部补强前更加均匀。

图10 局部补强前后CAE变形结果

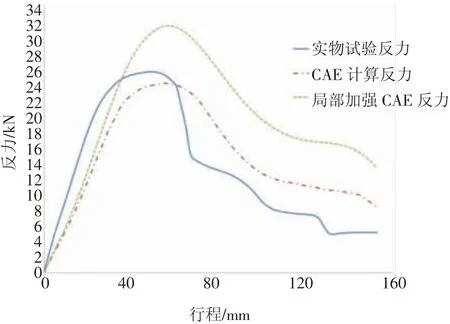
图11 实物和CAE F-S曲线

图11 为实物和CAE试验F-S曲线，实物试验平均反力为13.33 kN，CAE计算结果为14.69 kN，误差率为9.3%符合工程要求，可用于反力计算和预测。局部增加T1.0补强材后，平均反力增加了35%到19.89 kN。局部增强方案对于增加平均反力改善效果明显。

4 局部加强型M型防撞杆优化

M型防撞杆局部加强方案虽然能提高静压反力，但是同时也增加了零件重量。在轻量化和降油耗的严峻要求下，需要针对该方案进行多目标的优化。

4.1 优化流程

多目标优化问题中，一般存在2个或以上的目标存在冲突，其中一个目标的改善必定会导致另一个或多个目标恶化，多目标优化问题就是对目标之间的求取最优解的过程。其过程用数据模型描述如下：

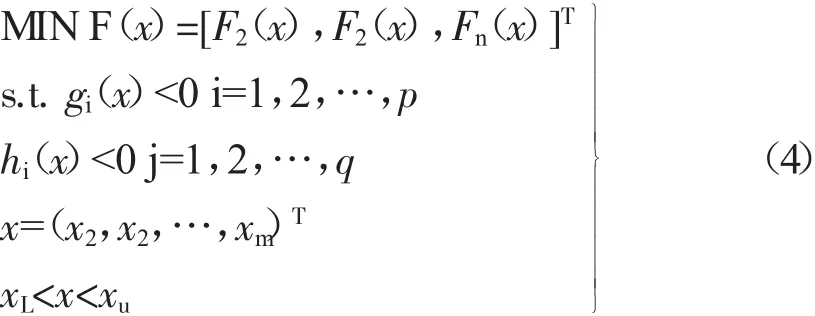
式中：F（x）——目标函数；

x——设计变量；

gi（x）、hi（x）——优化的约束条件；

n、p、q——函数的个数；

m——自变量个数；

xL和xu——分别为自变量上下限。

文章将选取防撞杆本体和局部补强材相关参数，设定防撞杆平均反力和质量为优化目标，进行DOE试验设计，构建RBF模型，进而利用遗传算法求出最优解。整个优化流程如图12所示。

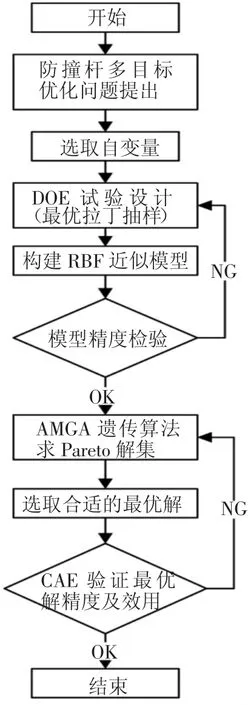
图12 多目标优化流程

4.2 参数选取

图13 为M型防撞杆主要参数，考虑到M型特征峰宽度a与整体宽W之前存在一定的几何关系，最终选取以下6个独立变量（X1～X6），变量的取值范围选择通常使用的范围，如表3所示。

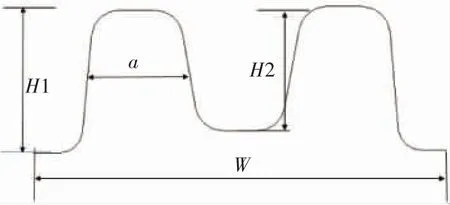
图13 M型防撞杆断面

表3 变量因子及其取值范围

4.3 试验设计DOE

由于变量因子较多，为了在变量组合的抽样空间内，更均匀的进行试验设计，选择最优拉丁方（LHS）抽样进行试验设计[6]，通过对相关试验组进行CAE计算得到平均反力Y1和质量M。试验设计如表4所示。

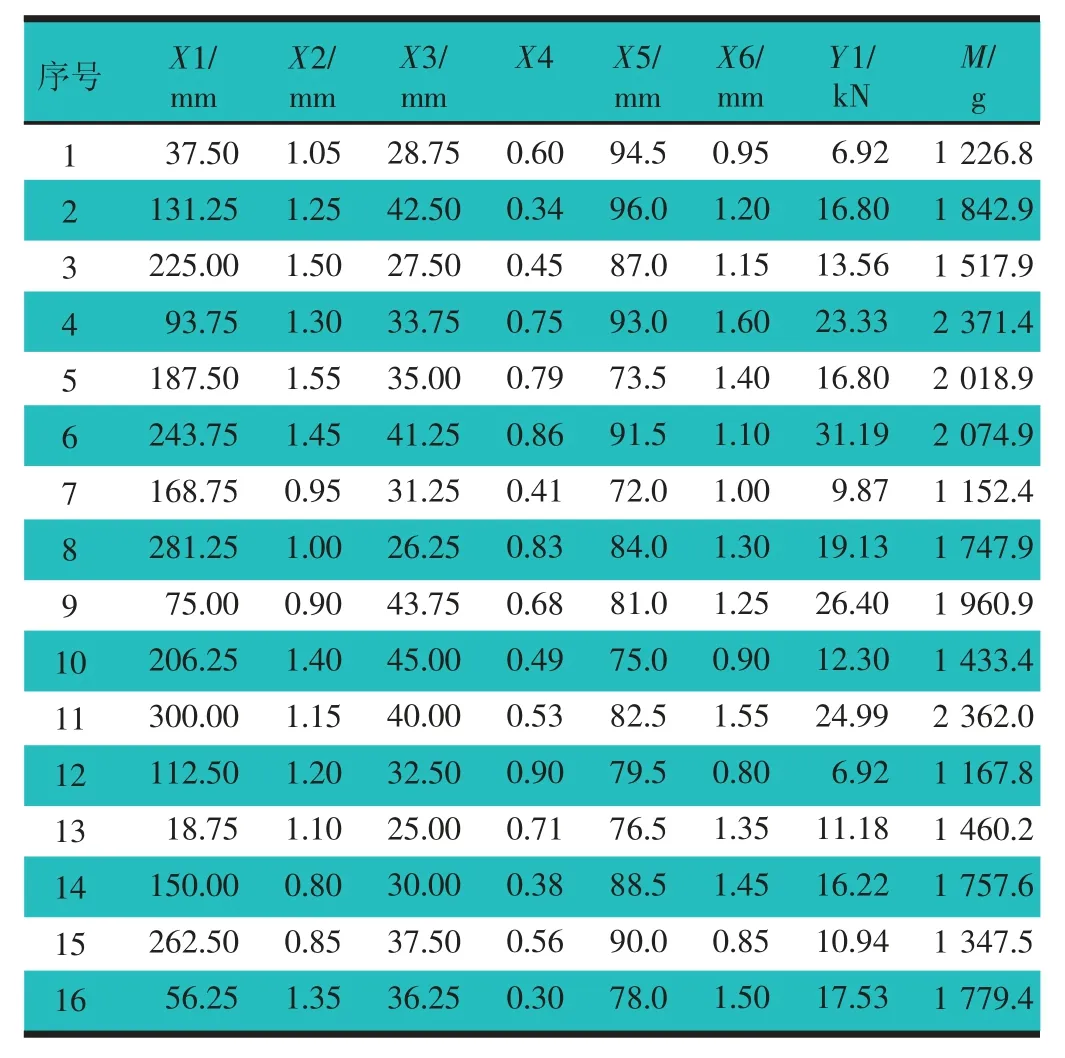
表4 DOE及CAE计算值

4.4 建立RBF模型及误差检验

通常对于非线性问题的预测模型有BRF，Kriging插值，RSF响应面等方法，文章选择径向基(RBF)函数神经网络方法建立模型。其原理如图14所示，第1层为输入层，由信号源节点组成；第2层为隐藏层，隐藏层是对高斯函数的参数进行调整，采用的是非线性优化策略；第3层为输出层，对线性加权进行调整[7]。其中，X代表输入，y代表输出，p代表中间的隐藏层。

图14 RBF神经网络原理

文章随机了4组数据进行CAE计算和RBF模型预测的精度检验，结果如表5所示。RBF的模型预测精度平均反力Y1在±10%以内，质量M精度±5%以内，精度较好，可用该模型进行响应值的预测，进而节省大量的CAE工时。

RBF模型各个自变量对于响应值的全局影响梯度如图15所示。局部补强材参数X1与X2虽然针对Y1和M单个响应的梯度影响较小，但是在Y1/M相对梯度方面较大。

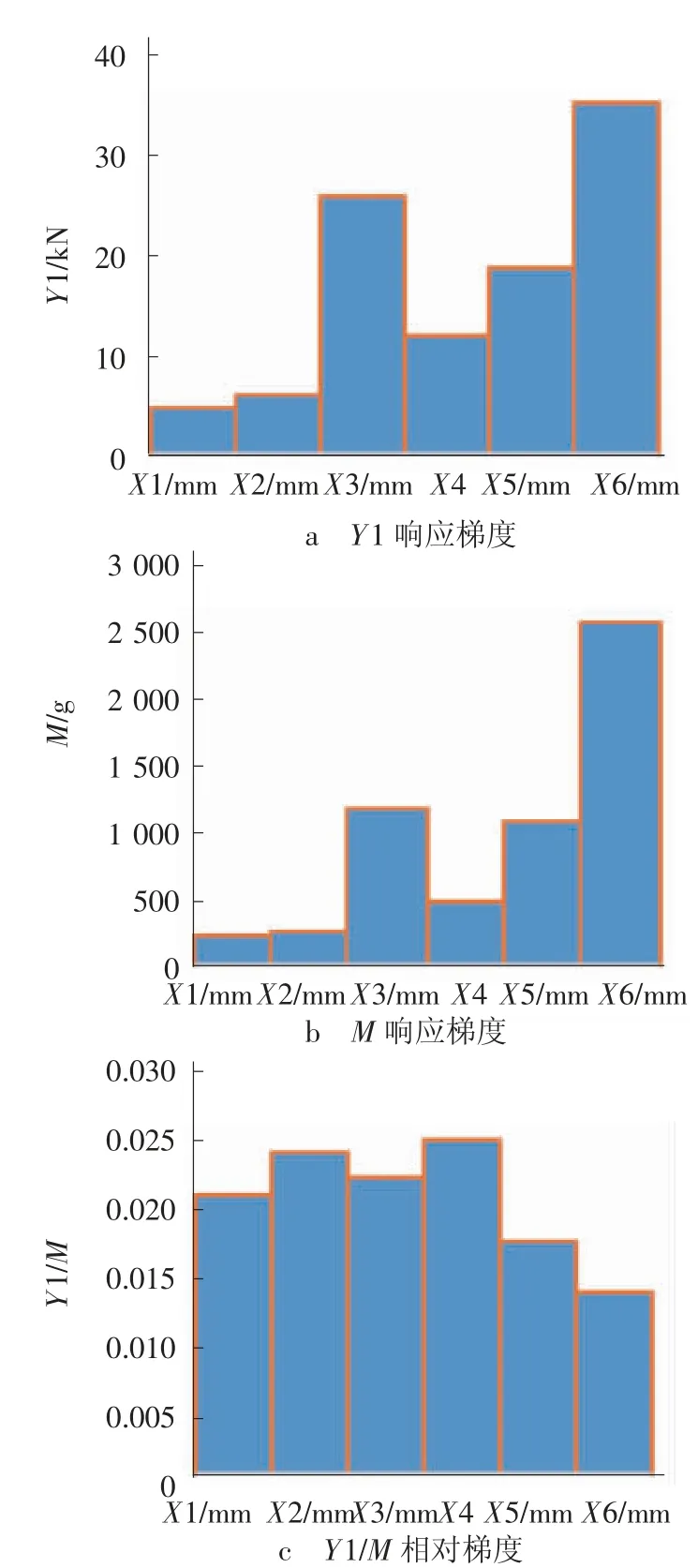
图15 各自变量响应梯度

表5 误差检验分析

4.5 基于AMGA多目标优化

AMGA是一种自适应多种群的遗传算法，主要采用改进的交叉和变异算子来引导种群进化，常用于多目标非线性的最优解进行求解[8]。

文章多目标的数据模型为：

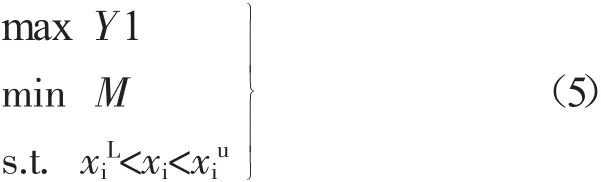
以最大化平均反力和最小化质量为目标求得该模型的Pareto图解，如图16所示。

图16 最优解Pareto前沿

以某1.5 GPa防撞杆参数作为初始化设计，其初始化质量为1.51 kg，CAE其计算平均反力为8.9 kN无法满足侧门挤压强度要求。在保持初始设计总质量不增加的情况下，使用Pareto解集求得更优的平均反力，优化前后的参数，如表6所示。

表6 优化前后对比

将优化前后的平均反力和质量计入，如表7所示，同时针对优化后的方案进行CAE试验。从对比结果可以看出，局部加强方案经过优化后，在质量基本不变的情况下，其平均反力增加64%达到14.6 kN，满足静态挤压强度要求，优化效果较好。

表7 优化效果

5 结论

1）通过不同形式车门防撞杆对比，M型热成形防撞杆相对钢管防撞杆，其反力和重量可达到相同水平，且具备弯曲随形的布置优点。

2）针对M型热成形防撞杆，提出了对应力集中的溃缩区域局部补强的方案，该方案相对补强前，可以提升30%以上平均反力。

3）针对局部加强的M型防撞杆以质量和平均反力为响应值，建立RBF模型，并通过AMGA遗传算法进行多目标优化，优化后，可在满足轻量化要求的前提下，进行平均反力的提升，效果明显。