一类非线性Hilfer分数阶微分耦合系统正解的存在性

甘亦苗， 侯成敏

（延边大学 理学院，延吉133002）

0 引 言

分数阶微分方程在科学与工程学中应用广泛，如物理、生物、化学和电子等［1-3］。带有边值问题的耦合系统在众多的领域上取得了重大成就［4-6］，在处理正解的存在唯一性上方法多样［6-7］。Hilfer型分数阶导数是广义的Riemann-Liouville分数阶导数，其包含Riemann-Liouville和Caputo分数阶导数两种情形［1］，此类导数可以应用于玻璃成型材料中介电驰豫的理论模型［9］。

本文研究高阶的非线性耦合Hilfer分数阶微分系统的正解的存在性：

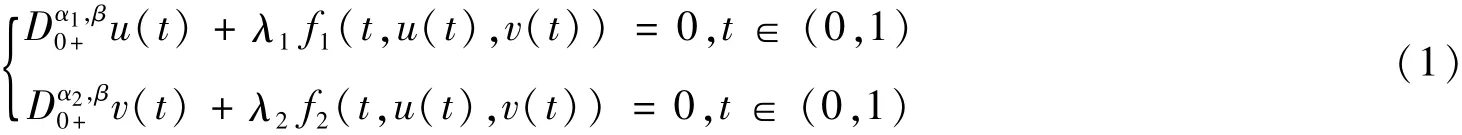
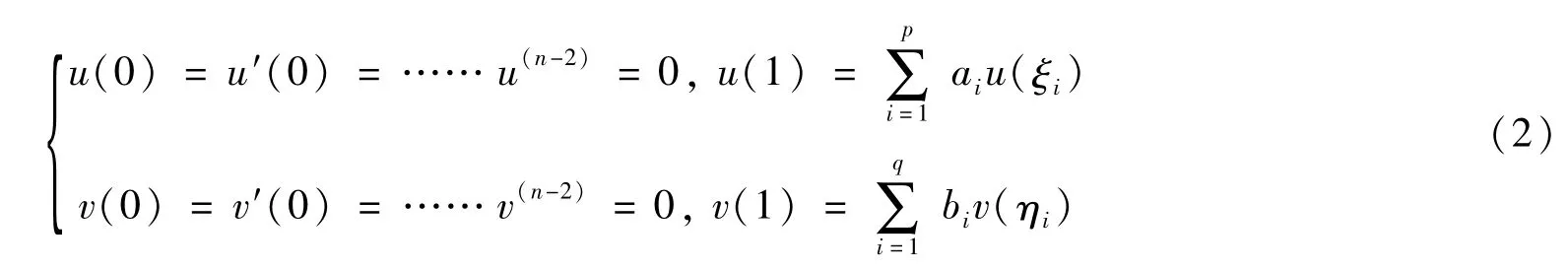
式中：是Dα1，β0+，Dα2，β0+为Hilfer分数阶导数，n，m为正整数n-1＜α1＜n，m-1＜α2＜m，0≤β≤1，p，q∈ℕ，λ1，λ2∈ℝ+，ai∈ℝ（i=1，2，…p），bi∈ℝ（i=1，2，…q）且，0＜ξ1＜…＜ξp＜1，0＜η1＜η2＜…＜1，fj（j=1，2）为连续函数。

许多文献在研究方程的解时，设fj是非负的或者单调的（［5，7，10］），为了使文章更具有一般性，本文不做以上假设，并且利用换元法和Guo-Krasnosel’skii不动点定理证明正解的存在性。

1 预备知识和相关引理

有唯一的解：

其中

证明完毕。

根据引理4，易知问题（1）和问题（2）的解为：

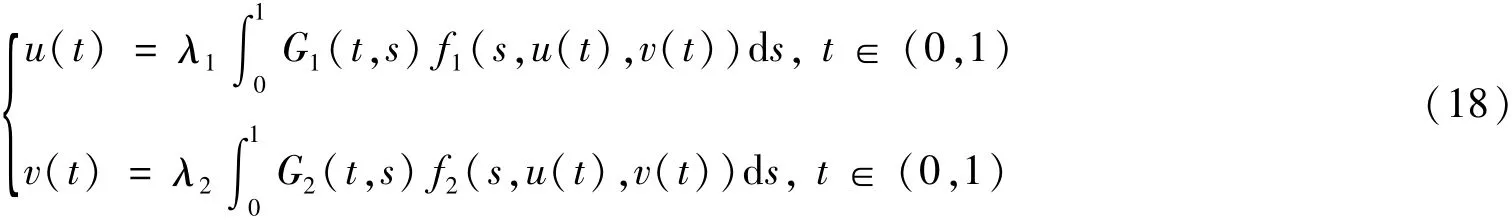
其中

2 主要成果

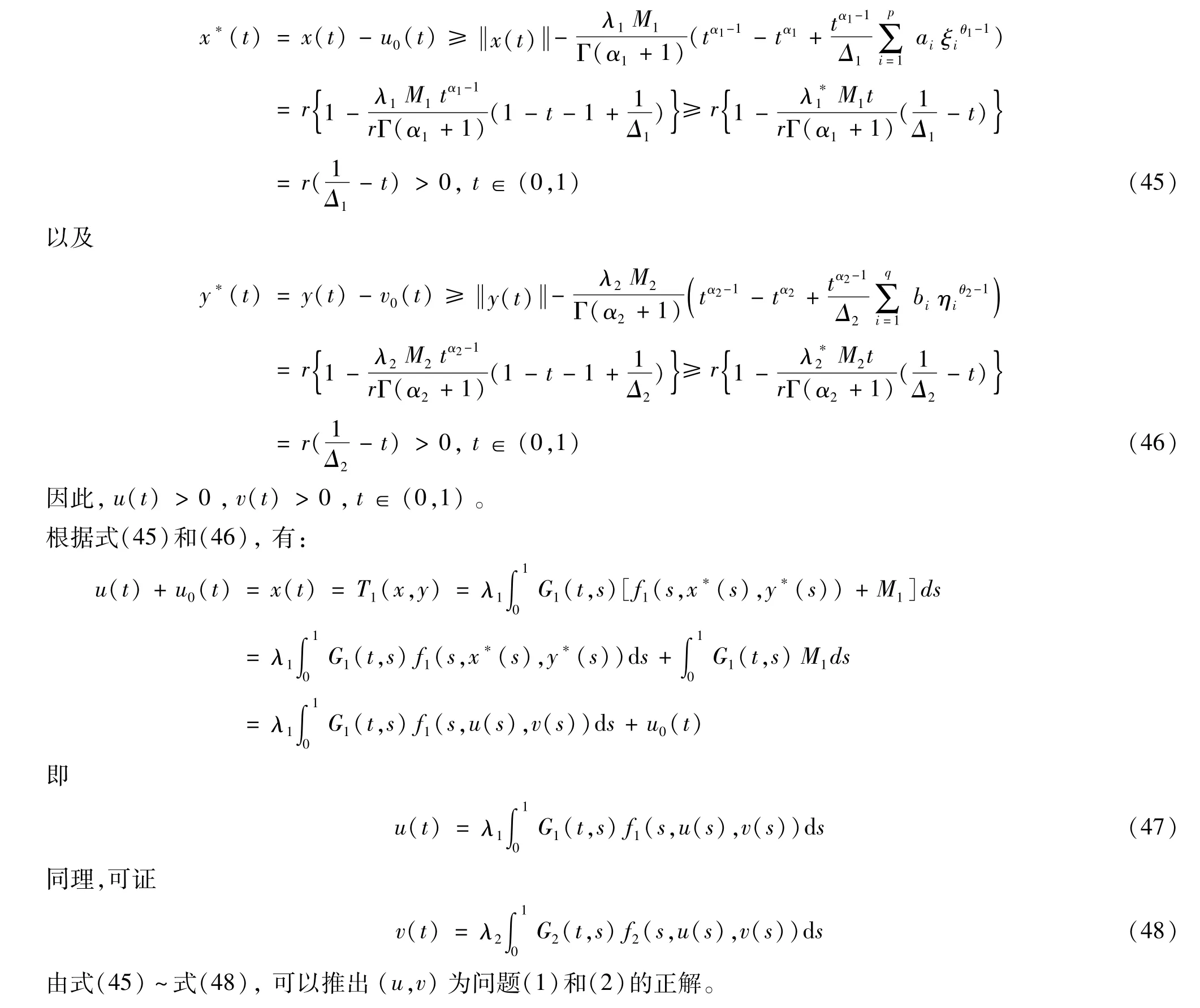
3 一个例子

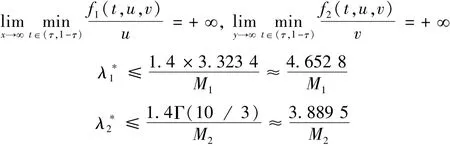
这就意味着（H1）和（H2）成立。由定理1可得，问题（49）和（50）至少存在一个正解。