带有状态时滞的非线性随机系统高斯滤波方法

王 硕， 何定洲， 朱 勇， 沈敦亮， 于 霖

（中国运载火箭技术研究院 北京宇航系统工程研究所，北京100076）

0 引 言

时滞问题的存在会对系统运行造成不良的影响，如造成系统振动、性能退化和甚至失稳等现象。近年来，在信号处理、通信和控制等领域采用非线性离散随机系统，而对其非线性状态的获得大多利用观测数据来近似估计［1-4］。通常，对非线性离散随机系统的状态估计问题的研究主要集中在一阶随机模型或一阶马尔可夫模型。但在实际应用中，很多机械和电气动态系统则是二阶模型或高阶非线性连续时间随机模型，不是一阶模型［5-6］。这种高阶连续时间模型进行离散化时，必然会出现时滞的状态。因此，需要研究一种能够对带有状态时滞的非线性离散随机系统进行近似估计的方法。

对于带有状态时滞的非线性状态估计问题通常采用H∞滤波［7-8］和粒子滤波［9-10］等方法进行解决，针对此问题学者们开展了大量的研究。Shi和Shan等对带有时变状态时滞和随机状态时滞控制系统的稳定性进行了研究［11-12］。Gu等针对带有多状态时滞的状态空间问题，提出了最小二乘辨识算法［13］。Fang等对离散线性系统同步输入和状态估计的稳定性进行了研究［14］。Shi等针对带有两步随机时滞的网络控制系统提出了鲁棒混合H2/H∞控制器［15］。文献［16］给出了带有d步状态时滞的多变量状态估计方法，在此基础上，文献［17］提出了联合估计系统参数和状态递归最小二乘方法。虽然这些方法不需要对概率密度函数（Probability density function，PDF）进行任何假设，但为了得到更高的估计精度，采用粒子滤波算法不可避免地会因为大量的随机样本而产生巨大的计算量，或采用H∞滤波需要复杂的计算矩阵不等式。特别对于带有状态时滞的情况，这些复杂的计算量会进一步增加。主要是因为当把状态时滞认定为非线性离散随机系统的一部分时，除了要对当前状态进行近似估计外，所有的状态时滞也要进行近似估计，这必然会产生更大的计算量。因此，需要研究一种状态时滞的高斯滤波算法。

对于一般的非线性离散系统，常用的高斯滤波（GF）框架没有考虑带有状态时滞的情况［18］。在GF框架下，通过不同的数值计算形式来近似非线性积分已经取得大量的研究成果。其中，最为突出且被广泛应用的是扩展卡尔曼滤波器（EKF）［19-20］，它是通过对非线性方程的一阶线性化得到的。但是一阶线性化得到的近似精度不高，经常会出现重大的偏差，甚至产生发散的情况。此外，其对雅可比矩阵的推导也是不容易的，尤其面对高维和不连续非线性系统的情况。

在文献［18］的GF框架下，基于确定性采样的数值技术来近似非线性积分，已取得了大量的研究成果，包括基于无迹变换的无迹卡尔曼滤波器（UKF）［22-23］、基于正交规则的高斯埃尔米特滤波器（GHF）、基于斯特林多项式插值的差分滤波器（DDF）和中心差分滤波器（CDF）等［24-26］。这种基于GF的确定性采样不需要计算雅可比矩阵，且计算复杂度与EKF类似［21］。但他们至少可以达到二阶的近似精度，高于EKF的一阶近似精度。熊和吴等提出了一套关于精度、效率和稳定性的性能指标来分析和比较这些滤波器，促进在实际应用中对不同滤波器的选择，且给出了上述滤波器稳定的充分条件［27-28］。

Arasaratnam等针对UKF、EKF、DDF和GHF不适合处理高维非线性系统的问题，基于球径容积法则进一步提出了容积卡尔曼滤波器（CKF）［29］。Jia等提出一种新的非线性稀疏网格正交滤波器（SGQKF），精度比UKF、CDF、DDF和CKF更高，计算效率也比GHF更好［30］。陈红梅等将SGQKF应用在观测信息不完全且随机干扰不确定的非线性系统，并给出算法稳定性的证明［31］。Wang等针对过程噪声和量测噪声相关的非线性系统设计了一种高斯近似递归的滤波器［32］。

上述GF算法均是建立在同一假设条件下，即不考虑系统带有状态时滞的情况。但在实际工程的应用中，时滞问题一直存在。目前，针对带有状态时滞非线性随机系统最优估计问题的解决尚不够完善，尤其对系统状态时滞和量测时滞同时存在的情况研究甚少。受文献［18］启发，本文针对带有状态时滞系统的最优估计问题，提出了一种新的高斯滤波框架，给出了其在三阶球径容积法则下的具体实现形式—状态时滞容积卡尔曼滤波器（SDCKF），可以很好地解决系统带有状态时滞的非线性估计问题，易于工程实现。

1 问题描述

考虑具有多个状态时滞的非线性离散随机系统，具体形式为：

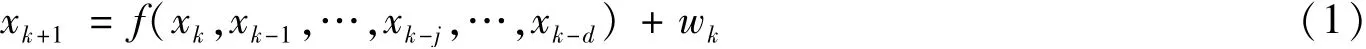
2 带有状态时滞的GF算法

由上述描述可知，标准GF算法未考虑系统带有状态时滞的情况。对标准GF算法进行改进，如式（1）

2.1 时间预测

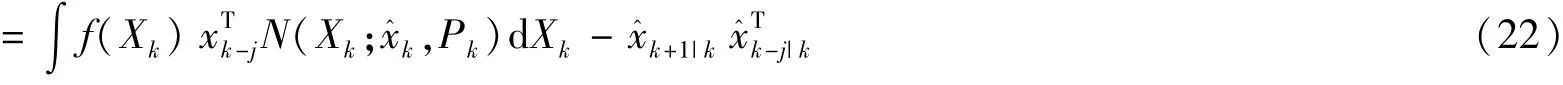
2.2 量测更新

2.3 带有状态时滞的GF算法实现

由定理1和定理2不难发现，对于多维高斯加权积分的计算问题，是实现本文所提出改进GF算法的主要难点。针对此问题，本文拟采用数值积分来近似非线性函数的方法实现。三阶球径容积法则是近些年提出的，且是较优越的线性化方法，该方法具有良好的数值稳定性和近似精度。因此，本文给出基于三阶球径容积法则的改进GF算法—SDCKF滤波算法。三阶球径容积法则如下：

2.3.1 三阶球径容积法则

针对式（14）～式（16）、式（26）和式（28）的非线性高斯加权积分，可以统一为如下形式：

3 仿真分析

通过非线性模型式（50）和式（51）来验证本文所提出SDCKF算法的有效性，并从非线性状态估计精度

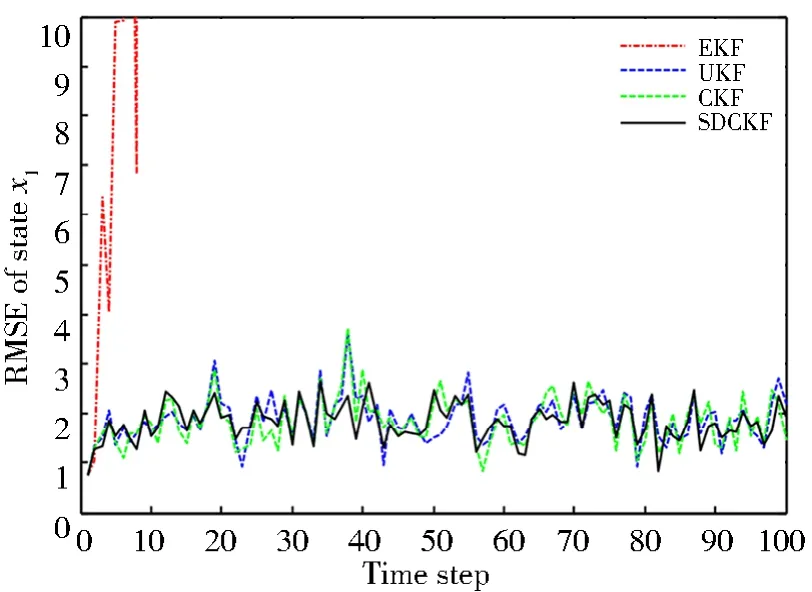
图1 状态x1的RMSEFig.1 RMSE of state x1

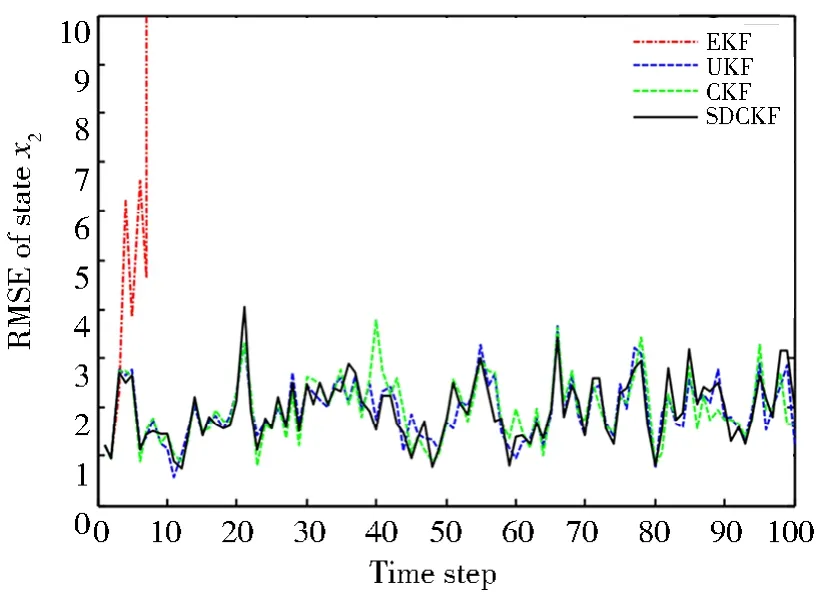
图2 状态x2的RMSEFig.2 RMSE of state x2

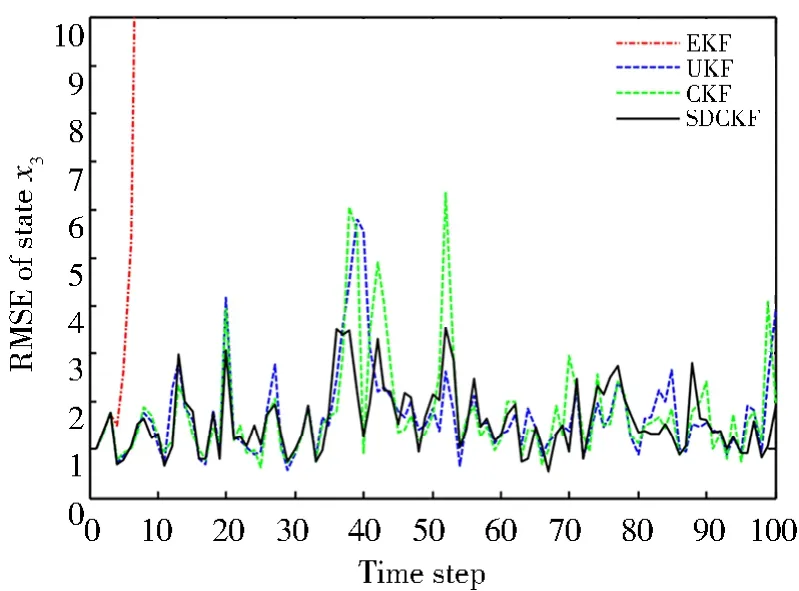
图3 状态x3的RMSEFig.3 RMSE of state x3

从仿真结果可以看出，EKF算法很快便出现了发散现象，表明EKF算法面对模型式（50）这种带有状态时滞的强非线性状态估计问题，很难进行状态估计。出现这种现象的原因可能是EKF算法在进行后验状态估计时对非线性方程的线性化误差变大，导致逼近非线性函数的雅可比矩阵发散，进而使得系统失稳。UKF算法和CKF算法也都获得了比较好的状态估计结果，数值稳定性较高。但是，由于系统状态时滞的存在，使得UKF算法和CKF算法的状态估计精度有所下降，在图3中表现比较明显，在仿真第40步和50步时误差突然变大，这可能是状态x3综合了状态x1和状态x2的误差所导致，这种状态估计误差突然变大的现象，在实际工程应用中可能会带来非常严重的后果。可以看出，本文所提出的SDCKF算法与UKF算法、CKF算法几乎具有相同的状态估计精度，或略高于这两种算法。但是，SDCKF算法的数值稳定性明显高于UKF算法和CKF算法，SDCKF算法未出现误差跳变、突然增大等情况。综合上述分析结果，本文所提出的SDCKF算法可以很好地解决带有状态时滞的非线性随机系统的状态估计问题。

4 结 论

针对传统高斯滤波算法不能很好地解决系统带有状态时滞的非线性状态估计问题，给出了一种改进的高斯滤波算法-状态时滞容积卡尔曼滤波器（SDCKF）。给出了在三阶球径容积法则下的具体实现形式，可以有效地避免因为状态维数过高而引起滤波算法稳定性下降的问题。通过带有状态时滞的非线性函数示例，将SDCKF算法与经典非线性滤波方法EKF算法、UKF算法及CKF算法进行仿真对比分析。仿真结果表明，SDCKF算法具有更好的数值稳定性和状态估计精度，证明了SDCKF算法可以很好地解决系统带有状态时滞的非线性状态估计问题。