基于主瓣保形的低旁瓣MIMO雷达发射方向图优化设计方法

黄俊生

（中国电子科技集团公司第二十研究所，西安 710068）

0 引言

多输入多输出（Multiple Input Multiple Output，MIMO）雷达是近几年来研究比较多的一种新体制雷达，一经提出便让众多学者为之着迷和振奋[1-5]。根据雷达天线位置分布方式的不同，MIMO 雷达可以划分为集中式MIMO 雷达[6-7]和分布式MIMO 雷达[8-9]两大类。对于分布式MIMO 雷达而言，其收发天线之间的间距相对较大，由于每根天线对目标有着不同的观测视角，因此可以有效地克服目标闪烁效应所带来的影响，进而提高雷达系统对目标的检测以及跟踪能力。对于集中式MIMO 雷达而言，其收发天线之间的间距相对较小，并且天线的分布方式与相控阵雷达的天线分布方式很相似。但是相比于相控阵雷达，集中式MIMO 雷达能够获得较高的角度估计精度[10]、较好的参数识别能力[11]以及较强的杂波抑制能力[12]等。此外，由于集中式MIMO雷达的每根发射天线所发射的波形不但可以是正交的，而且也可以是部分相关的，因此集中式MIMO 雷达的发射波形协方差矩阵的秩将大于等于1，使其拥有更多的发射自由度，从而可以通过对发射波形协方差矩阵进行优化设计来灵活地综合出各种满足实际需求的发射方向图，以提升雷达系统在杂波抑制、抗干扰以及多目标跟踪等方面的性能。本文将主要对集中式MIMO 雷达（以下简称MIMO 雷达）的发射方向图优化设计方法进行研究。

对于MIMO 雷达，发射宽波束可以在不进行扫描的情况下实现大范围空域的监视，能够获得更多的目标信息，有助于实现多目标的检测或者跟踪[13]。因此，在目标检测或者跟踪过程中，加宽发射方向图的3 dB 主瓣宽度可以有效地提高MIMO 雷达系统的性能。此外，在发射方向图设计过程中，低旁瓣水平是一个非常重要的性能指标[14]。降低发射方向图的旁瓣水平不但可以将雷达系统的发射能量集中在主瓣区域，以提高雷达系统对目标的检测概率以及跟踪精度，而且可以降低来自旁瓣区域中的杂波信号和虚假目标信号的能量。

文献[15]提出了一种基于MIMO 雷达的低旁瓣发射方向图优化设计方法，其在各个天线的发射能量相同等约束条件下，以最大化主瓣指向功率和旁瓣峰值功率的差异为准则构造优化模型来对发射波形协方差矩阵进行优化设计。虽然利用该方法综合得到的发射方向图具有较低的旁瓣水平，但是该方法对3 dB 主瓣宽度的选取较为敏感。如果选取的3 dB 主瓣较宽，那么综合得到的发射方向图就会出现主瓣分裂的现象，进而影响雷达系统对目标的检测以及跟踪性能。由于降低发射方向图的峰值旁瓣水平可以有效地降低在电子对抗过程中被敌方所截获的或者被反辐射导弹所接收的信号能量，以及降低发射方向图的积分旁瓣水平可以有效地抑制旁瓣区域中的杂波信号和假目标干扰信号，因此，为了进一步提高雷达系统的性能，基于最小化峰值旁瓣水平/积分旁瓣水平的MIMO 雷达发射方向图优化设计方法以及由它们所衍生出来的方法被相继提出[16-19]。然而，这些方法同样对3 dB 主瓣宽度的选取较为敏感。因此，我们希望找到一种新的发射方向图优化设计方法，使综合得到的发射方向图不但具有较低的旁瓣水平，而且具有期望的主瓣形状。

针对于此，为了有效地避免主瓣分裂现象并降低发射方向图的峰值（积分）旁瓣水平，本文提出一种基于主瓣保形的低旁瓣MIMO 雷达发射方向图优化设计方法。首先，利用一组满足共轭对称性质且相互之间不相关的基矩阵分别对发射波形协方差矩阵和更新矩阵进行线性表示。其次，通过约束主波束区域内任意两点之间的线段总是在主波束区域的内部来有效地避免主瓣分裂现象，以及利用更新矩阵更新发射波形协方差矩阵的非对角线元素来有效地降低发射方向图的旁瓣水平，并以最大化发射方向图的峰值（积分）旁瓣功率与主瓣指向功率的比值和更新的发射方向图的峰值（积分）旁瓣功率与主瓣指向功率的比值之和为准则构造优化模型来同时对发射波形协方差矩阵和更新矩阵进行优化设计。接下来，利用优化得到的发射波形协方差矩阵和更新矩阵综合出满足实际需求的发射方向图。最后，仿真实验结果证实了本文所提方法的有效性。

1 MIMO 雷达发射信号模型

考虑一个如图1所示的MIMO 雷达系统，其为包含M个天线阵元的均匀线阵（Uniform Linear Array，ULA），且阵元之间的间距为d。假设第m个发射阵元所发射的离散时间基带波形为sm，且sm∈C1×L，其中，L为发射波形的长度，则所有发射阵元发射的波形到达空间角度为θ处的远场信号可以表示为：

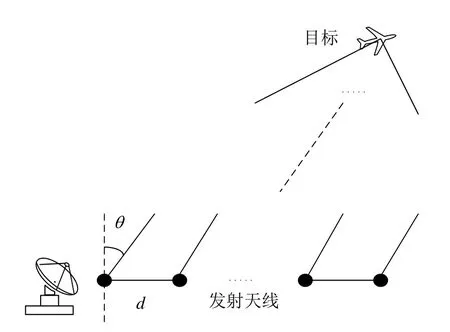
图1 MIMO 雷达发射阵列结构

式中，（·）H为取共轭操作。

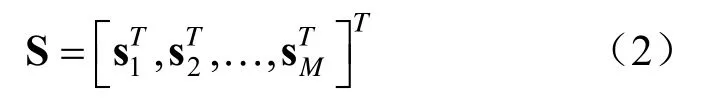
式（2）为发射波形矩阵，发射导向矢量a(θ) 可以表示为：

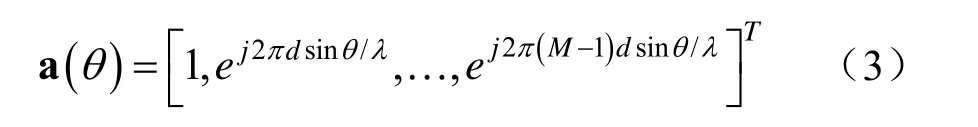
式中，（·）T为取转置操作，λ为雷达系统的操作波长。

因此，空间角度θ处的信号功率可以进一步表示为：

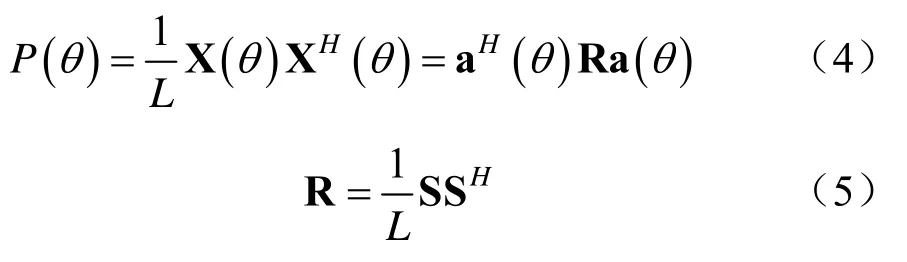
式（5）为发射波形协方差矩阵。P（θ）即为MIMO 雷达的发射方向图，可以根据不同的实际需求来进行优化设计。

2 基于主瓣保形的低旁瓣MIMO 雷达发射方向图优化设计方法

当发射天线阵列的结构和数目固定时，发射方向图固有的3 dB 主瓣宽度将被唯一确定。

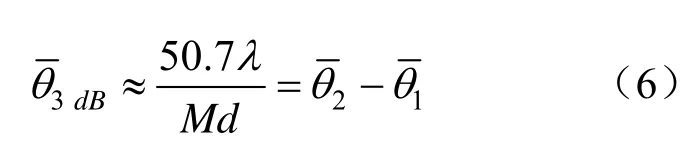
其中，和为对应于3 dB 主瓣宽度的3 dB角度。在目标搜索或者跟踪过程中，加宽发射方向图的3 dB 主瓣宽度能够有效地提高MIMO 雷达系统的性能，然而大多数现有的发射方向图设计方法都对3 dB 主瓣宽度的选取很敏感。如果所选取的3 dB 主瓣宽度太宽于，则综合得到的发射方向图就会在3 dB角度和处产生两个较深的零陷，造成主瓣分裂现象的产生，进而影响雷达系统对目标的检测或者跟踪性能。尽管可以通过增加对3 dB角度和的约束来有效地避免主瓣分裂现象的产生，但是对应于这两个角度的增益值往往是很难确定的。此外，在发射方向图设计过程中，低旁瓣水平同样也是一个非常重要的指标。因此，本文提出了一种基于主瓣保形的低旁瓣MIMO 雷达发射方向图优化设计方法，以有效地避免主瓣分裂现象的产生并降低发射方向图的旁瓣水平。

2.1 基矩阵构造

由于发射波形协方差矩阵R 具有共轭对称性质，也就是满足 R =RH，因此可以利用一组相互之间不相关且满足共轭对称性质的基矩阵来对发射波形协方差矩阵R 进行线性表示。同时，这些基矩阵可以分别表示为：

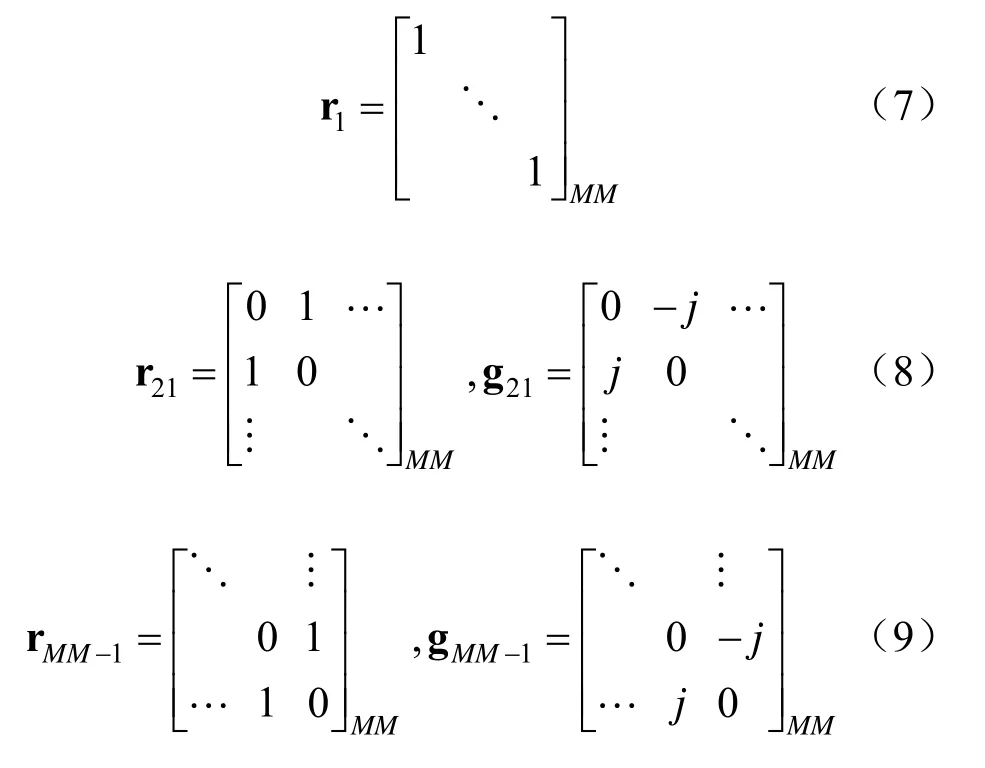
式中，r1是一个M维的单位矩阵，rmn用来表示基矩阵的第（m,n）个元素和第（n,m）个元素的值为1，且其它元素的值为0，gmn则用来表示基矩阵的第（m,n）个元素的值为j，第（n,m）个元素的值为-j，且其它元素的值为0，m= 2,3,…M，n= 1,2,…m。则发射波形协方差矩阵R 可以利用这些基矩阵线性表示为：

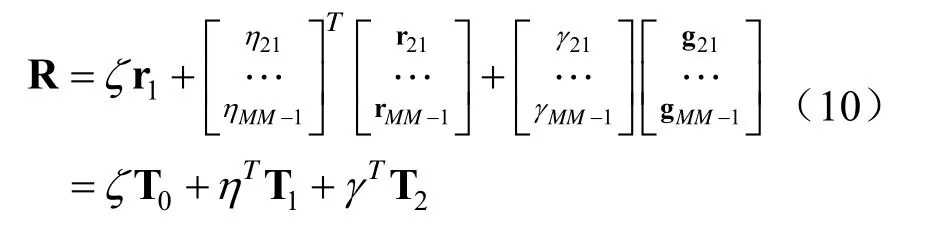
式中，r1是一个M维的单位矩阵，rmn用来表示基矩阵的第（m,n）个元素和第（n,m）个元素的值为1，且其它元素的值为0，gmn则用来表示基矩阵的第（m,n）个元素的值为j，第（n,m）个元素的值为-j，且其它元素的值为0，m= 2,3,…M，n= 1,2,…m。则发射波形协方差矩阵R 可以利用这些基矩阵线性表示为：

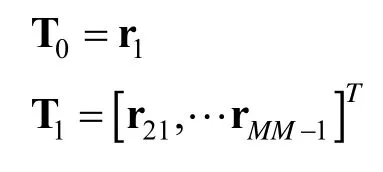
从式中能够明显地看出，可以通过优化这些基矩阵的系数ζ、η 和γ 来代替直接对发射波形协方差矩阵R 进行优化设计。

2.2 发射波形协方差矩阵优化设计

由于发射方向图的主瓣区域具有凸的形状，因此可以通过确保发射方向图主瓣区域内任意两点之间的线段总是在主瓣区域的内部来有效地避免主瓣分裂现象的产生。由于发射波形协方差矩阵的对角线元素表示每根天线的发射能量，且这些对角线元素上的值在每根天线的发射能量相同的约束条件下是固定且相等的，因此可以利用一个对角线元素为0 且同样具有共轭对称性质的更新矩阵来对发射波形协方差矩阵的非对角线元素上的值进行更新，以有效地降低发射方向图的旁瓣水平。此外，如果想要降低在电子对抗中被敌方所截获的或者被反辐射导弹所接收的信号能量，则可以通过构造最小化发射方向图的峰值旁瓣功率和主瓣指向功率的比值与更新的发射方向图的峰值旁瓣功率和主瓣指向功率的比值之和的优化模型来同时对发射波形协方差矩阵和更新矩阵进行优化设计；如果想要有效地抑制旁瓣区域中的杂波信号和假目标干扰信号，则可以通过构造最小化发射方向图的积分旁瓣功率和主瓣指向功率的比值与更新的发射方向图的积分旁瓣功率和主瓣指向功率的比值之和的优化模型来同时对发射波形协方差矩阵和更新矩阵进行优化设计。在本文中，我们将以前者为例进行介绍，其相应的优化模型可以表示为：

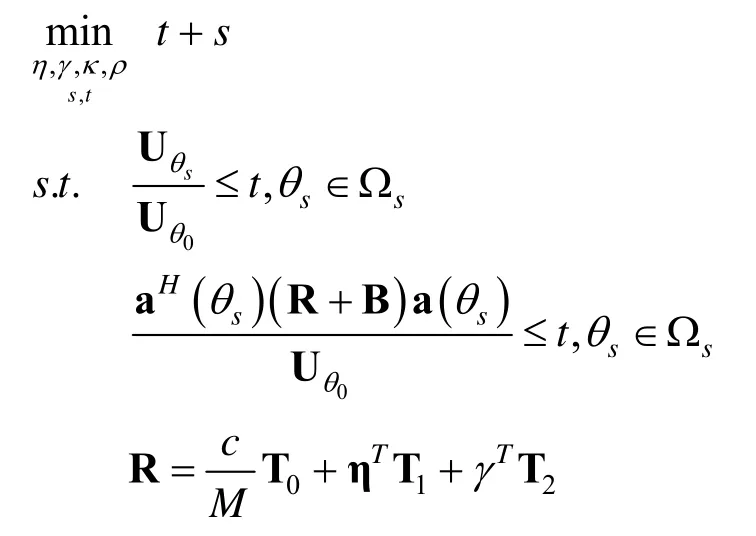
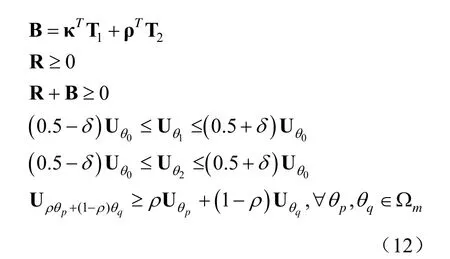
式中，Up=aH（θp）Ra（θp）表示θp方向的功率，Ωm为发射方向图的主瓣区域，Ωs为发射方向图的旁瓣区域，θ0为主瓣指向方向，θ1和θ2为预设定的3 dB 角度，c为雷达系统总的发射能量，δ是一个非常小的值，0≤ρ≤ 1用来约束主瓣区域的形状。第一行约束条件用来最小化发射方向图的峰值旁瓣功率和主瓣指向功率的比值。第二行约束条件用来最小化更新的发射方向图的峰值旁瓣功率和主瓣指向功率的比值。第三行约束条件用来表示发射波形协方差矩阵R 以及约束每个天线具有相同的发射能量。第四行约束条件则用来表示更新矩阵B以及更新矩阵的对角线元素全为0 且同样具有共轭对称性质。第五行和第六行约束条件分别用来确保发射波形协方差矩阵和更新的发射波形协方差矩阵具有半正定性。第七行和第八行约束条件用来约束发射方向图的3 dB 主瓣宽度。最后一行约束条件用来确保主瓣区域内任意两点之间的线段总是在主瓣区域的内部。

由于第一行和第二行约束条件的存在，式（12）不是一个凸优化问题，并不能直接利用现有的凸优化工具包进行求解，为此，我们将分两个步骤来对式（12）进行求解。第一步，将主瓣指向功率设置为1，则式（12）将转化为最小化发射方向图的峰值旁瓣功率与更新的发射方向图的峰值旁瓣功率之和。同时，其相应的优化模型可以进一步表示为：

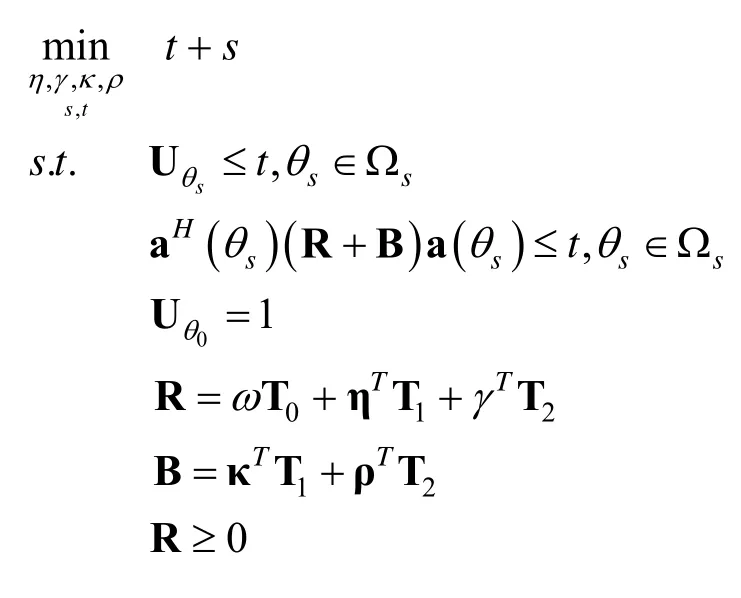
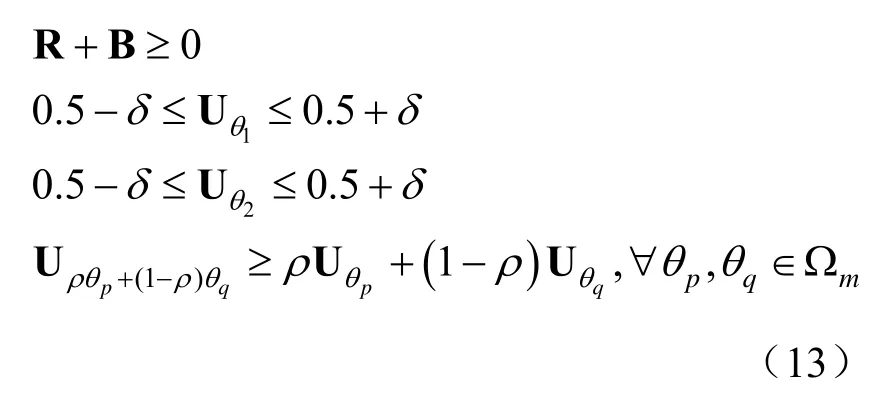
式中，约束条件 R =c/M T0+ ηTT1+γTT2被松弛为R =ωT0+ ηTT1+γTT2，也就是将每根天线的发射功率转化成了一个待优化变量。同时，式（13）是一个凸优化问题，可以直接利用现有的凸优化工具包进行求解，比如 CVX[20]，并得到最优解为

在式（13）中，由于发射方向图的主瓣指向功率被设置为1，因此其根本不满足式（12）中雷达系统总的发射功率为c的约束条件。同时，由于式（12）中的第一行和第二行约束条件对发射波形协方差矩阵R 具有尺度不变性，因此，在第二步中，可以利用式（14）来获得更新的发射波形协方差矩阵：

此外，上述所提出的发射波形协方差矩阵优化设计方法同样可以应用到多波束的情况。具体来说，通过确保发射方向图中每个主波束区域内任意两点之间的线段总是在该主波束区域的内部来有效地避免主瓣分裂现象的产生，以及利用更新矩阵更新发射波形协方差矩阵的非对角线元素来有效地降低发射方向图的旁瓣水平，并以最小化发射方向图的峰值旁瓣功率和发射方向图的最大功率的比值与更新的发射方向图的峰值旁瓣功率和发射方向图的最大功率的比值之和为准则构造优化模型来同时对发射波形协方差矩阵和更新矩阵进行优化设计。假设需要形成K个波束，则其相应的优化模型可以表示为：

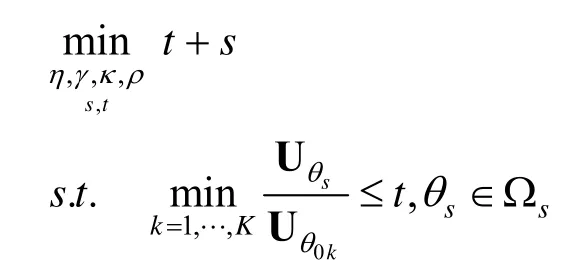
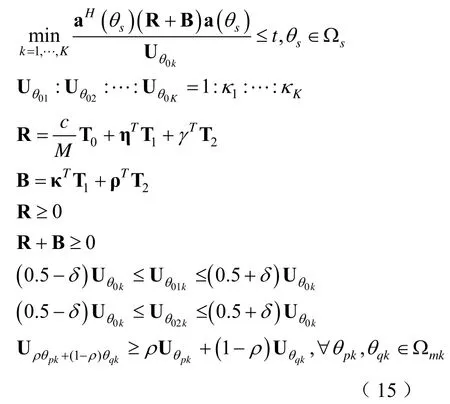
式中，Ωmk为发射方向图的第k个主波束区域，θ0k为第k个主波束的指向方向，θ1k和θ2k为对应第k个主波束的预设定的3 dB 角度，k= 1,2, …,K。第一行约束条件用来最小化发射方向图的峰值旁瓣功率和发射方向图的最大功率的比值。第二行约束条件用来最小化修正的发射方向图的峰值旁瓣功率和发射方向图的最大功率的比值。第三行约束条件用来表示每个主波束指向方向的增益之比。第八行和第九行约束条件用来约束发射方向图的第k个主波束的3 dB 主瓣宽度。最后一行约束条件则用来确保发射方向图的第k个主波束区域内任意两点之间的线段总是在该主波束区域的内部。此外，其余约束条件与式（12）中相应的约束条件具有相同的含义。同时，该优化问题同样可以按照求解式（12）的方法进行求解。

3 仿真实验

假设一个MIMO 雷达系统包含M=20 个发射天线阵元，且阵元之间的间距为半波长。整个雷达系统的发射能量为1，用于松弛3 dB 主瓣宽度的参数δ设置为0.1，且用来约束主瓣形状的参数ρ设置为0.5。

为了证实本文方法的有效性，对最小化旁瓣发射方向图设计方法、最小化峰值旁瓣发射方向图设计方法以及最小化积分旁瓣发射方向图设计方法也进行了相同的实验。

3.1 较窄的3 dB 主瓣宽度

（1）单波束发射方向图

在该实验中，假设单波束发射方向图的主瓣指向为θ0=0°，3 dB 角度为θ1=4-°和θ2=4°，旁瓣区域为Ωs=[-90 °,-8 °]∪[8 °,90 °]，图2比较了利用上述所有方法综合得到的发射方向图。从图2中可以看到，当 3 dB 主瓣宽度较窄时，利用本文方法综合得到的发射方向图的主瓣形状和其它方法的很相似。同时，在所有参与实验的方法中，利用本文方法综合得到的发射方向图具有最低的峰值旁瓣水平或者积分旁瓣水平，从而证实了本文方法的有效性。

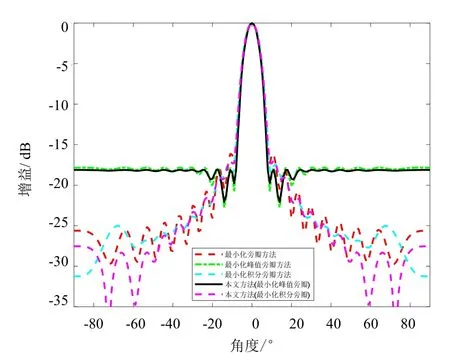
图2 主瓣3 dB 宽度较窄时综合得到的单波束发射方向图

（2）多波束发射方向图

当需要同时形成多个波束对目标信号进行检测或跟踪时。在此情况下，假设有三个波束，且指向分别为-40°、10°和50°，相应的3 dB 角度依次为-44°、-36°、6°、14°、46°和 54°。旁瓣区域为Ωs=[-90°,-48°]∪[-32°,2°]∪[18°,42°]∪[58°,90°]。三个束波指向方向的增益比是1:1:1，图3对比了利用本文方法和其它三种现有方法综合得到的发射方向图。从图中可以看出，类似于单波束的发射方向图，利用本文方法综合得到的发射方向图同样也具有最低的峰值旁瓣水平或者积分旁瓣水平。

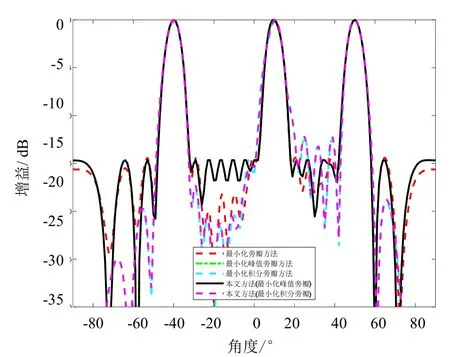
图3 主瓣3 dB 宽度较窄时综合得到的多波束发射方向图

4.2 较宽的3 dB 主瓣宽度

由于在对目标信号进行检测或者跟踪的过程中，加宽发射方向图的3 dB 主瓣宽度能够有效地提升雷达系统的整体性能，因此在以下的仿真实验中，我们将验证本文方法和其它现有方法在发射方向图所需要的3 dB 主瓣宽度较宽时的性能。

（1）单波束发射方向图

假设单波束发射方向图的主瓣指向为θ0=0°，3 dB 角度为θ1=-8°和θ2=8°，旁瓣区域为Ωs=[-90°，-15°]∪[15°，90°]，图4给出了利用上述所有方法在这种情况下综合得到的发射方向图。从图4可以清晰地看到，利用其它现有方法综合得到的发射方向图的主瓣区域严重变形，而本文方法通过对主瓣形状进行约束可以有效地确保综合得到的发射方向图具有期望的主瓣形状。此外，利用本文方法综合得到的发射方向图同样也具有较低的峰值旁瓣水平或者积分旁瓣水平，进而证实了本文方法的有效性。

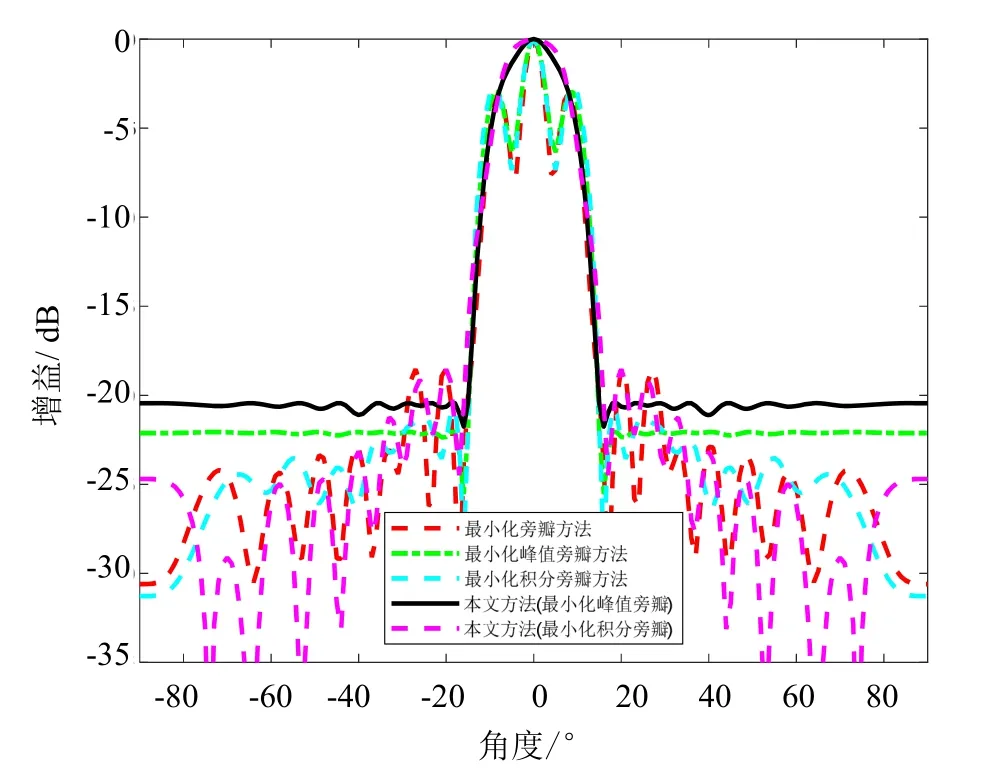
图4 主瓣3 dB 宽度较宽时综合得到的单波束发射方向图

（2）多波束发射方向图

假设需要三个波束，每个波束需要的3 dB 主瓣宽度都宽于其固有的3 dB 主瓣宽度时，三个波束的指向分别为-40°、10°和50°，相应的3 dB 角度为-48°、-32°、2°、18°、42° 和 58°，旁瓣区域为Ωs=[-90°,-56°]∪[-24°,6°]∪[26°,36°]∪[66°, 90°]。三个波束指向方向的增益比为1:1:1。在这种情况下，图5对比了利用本文方法和其它三种现有方法综合得到的发射方向图。从图中可以明显地看出，相比于其它三种现有方法，本文方法通过约束每个主波束区域内任意两点之间的线段总是在该主波束区域的内部可以有效地避免主瓣分裂现象的产生，有效地提高了雷达系统对目标信号的检测概率以及跟踪精度。

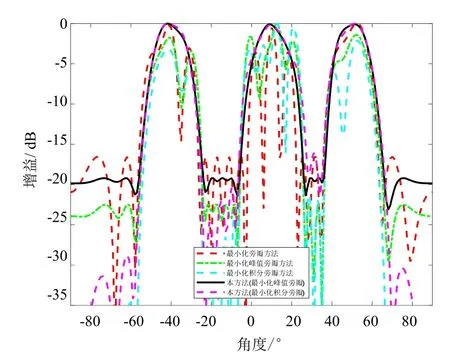
图5 主瓣3 dB 宽度较宽时综合得到的多波束发射方向图

5 结束语

为了有效地避免由较宽的3 dB 主瓣宽度所引起的主瓣分裂现象以及降低发射方向图的旁瓣水平，本文提出了一种基于主瓣保形的低旁瓣MIMO雷达发射方向图优化设计方法。由于发射方向图的主瓣区域具有凸的形状，因此该方法通过确保主瓣区域内任意两点之间的线段总是在主瓣区域的内部来有效地避免主瓣分裂现象。同时，由于在每个天线的发射能量相同的条件下发射波形协方差矩阵的对角线元素是固定且相等的，因此该方法利用一个对角线元素为0 的更新矩阵更新发射波形协方差矩阵的非对角线元素以有效地降低发射方向图的旁瓣水平。仿真结果表明，利用该方法综合得到的发射方向图具有期望的主瓣形状和较低的旁瓣水平，有效地提高了雷达系统对目标信号的检测概率以及跟踪精度。