存在近场辐射源情况下的阵列流形建模及分辨性能分析

宋嘉奇，王 露，王 珏

（中国电子科技集团公司第二十研究所，西安 710068）

0 引言

近场辐射源定位作为雷达、声呐系统的主要任务之一，在军事、民用等领域具有广泛应用。传统阵列信号处理通常假设信号源位于天线阵列的远场区域，也称夫琅霍费区（Fraunhofer Region），即信号源与阵列中心的距离r＞2D2/λ，其中D为传感器阵列的孔径，λ为无线电信号的波长。此时信号源与阵列的距离远大于阵列孔径，信号到达各阵元的波前差异不大，因此远场的电磁波传播模型可以用平面波来近似。但当信号源到阵列的距离满足0.62(D3/λ)1/2＜r＜ 2D2/λ时，目标位于天线阵列的近场区域，也称菲涅尔区（Fresnel Region），信号波阵面在天线阵列的孔径渡越无法忽略，此时信号到达阵列的波前需要用球面波模型进行描述，不能再近似为平面波[1]。从天线阵列中心到0.62(D3/λ)1/2的区域称为感应近场区，电磁能量在该区域内周期性地来回流动，不向外辐射。以11阵元的稀布天线阵列共线排布，阵元间距为5 m，天线工作在x波段，则阵列孔径D= 50 m，λ= 0.03 m ，2D2/λ≈ 1.67 × 105m，距离阵列中心小于150 km 的信号源都被视为近场目标，因此，研究近场情况下的辐射源参数估计问题具有非常重要的理论意义和实用价值。

参数估计算法中一类典型的参数估计算法是子空间类算法，自斯坦福大学的Schmidt 博士提出经典的多重信号分类（Multiple Signal Classification，MUSIC）算法[2]之后，国内外广大学者对子空间类算法开展了深入研究，并提出了一系列改进算法。特征子空间类算法的基本思想是利用特征分解将阵列接收数据矩阵分解为信号子空间和噪声子空间，通过对阵列流形（Array Manifold）的搜索实现信号源的参数估计，大大提高了参数估计精度及分辨率，且不再受“瑞利限”的约束。对于来自某特定方向的信号，阵列流形是阵列几何结构的直接函数，其中包含了辐射源的所有信息，研究阵列流形的性质不仅有助于分析目标定位的模糊度和分辨能力，同时对新的定位算法的提出和阵列结构的优化设计具有重要意义。

虽然阵列流形的概念广泛应用于信号源的参数估计问题，但仅有少量文献对阵列流形的形状直接进行研究。Manikas 提出，均匀线阵的远场阵列流形是N维复空间CN内的超螺旋曲线（hyperhelix），当所有阵元关于阵列质心中心对称时阵列流形的复超螺旋曲线为实值，同时指出反映参数估计性能的两个关键参数是阵列流形的弧长和一阶曲率[3]。帝国理工学院的Docus 和Manikas等人利用微分几何对不同阵型的远场阵列流形进行了研究[4]，并讨论了平面阵列方位角和俯仰角估计精度与其阵列流形微分几何特性的关系，并利用圆形近似推导出了用弧长和一阶曲率表示的克拉美罗界（Cramer-Rao Bound，CRB）表达式[5]。Karimi等人对均匀线阵接收近场球面波信号时的弧长和一阶曲率进行了推导，此时阵列流形不再是超螺旋曲线而是随信源距离的增大逐渐逼近于超螺旋曲线[6-7]。在国内，电子科技大学的刘洪盛博士分析了线阵和面阵的阵元位置误差与其测向性能的关系[8-9]，并提出了一种基于最小流形长度的高精度线阵优化设计方法[10]。何子远博士对稀疏阵的远场源估计模糊问题进行了分析，提出了一种利用功率估计去模糊的参数估计算法[11]。

本文以雷达和声呐系统的目标定位为背景，对近场参数估计的阵列流形进行了研究。第1 节建立了任意N元阵列接收近场辐射源信号的阵列流形模型，可以看出近场阵列流形是嵌在N维复空间CN中的复曲面，并对均匀线阵的远场阵列流形与近场阵列流形进行了对比；第2 节利用微分几何对一维线性阵列的近场阵列流形进行了分析，推导出了阵列流形弧长和一阶曲率的表达式；最后在第3节利用这两种局部特性参数对近场参数估计的分辨率和克拉美罗界进行了分析。

1 近场阵列流形建模

由N个阵元构成的任意阵列对K个信号源进行参数估计的问题模型通常被建立为以下阵列输出模型：

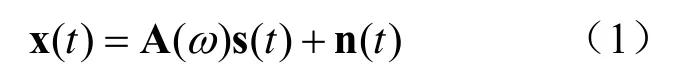
式中，x(t) 为阵列输出矩阵，s(t) 是信号的复包络矢量，n(t) 是阵列接收到的加性噪声，A()ω矩阵可以表示为以下形式：

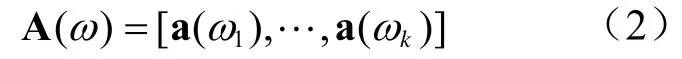
式中，ωk包含所有信号源的位置参数，a(ωk)为相应导向矢量（steering vector），表示阵列对位置参数为ωk的信源的响应。所有导向矢量的集合形成了一个轨迹或向量连续体，称为阵列流形。通常情况下，阵列流形被定义为从参数空间Ω 到CN的映射a。

式中，参数空间Ω 是所有可能的信源位置参数的集合。例如在远场源系统(ω=θ)中，Ω 是实数轴 R1上的开区间(0,2π)，因此远场阵列流形的图像是CN中关于θ的单参数曲线。当信号源位于近场区域(ω=θ,r)时，Ω是实数平面 R2上的开区间[(0,2π),(0.62(D3/λ)1/2,2D2/λ)]，阵列流形 a(θ,r)的图像则是CN中关于θ和r的双参数曲面。

推导阵列接收近场窄带信号的阵列流形表达式首先需要确定其球面波前。简单起见，假设只包含两个各向同性阵元的阵列，如图1所示，选取阵元1 为参考阵元（坐标原点），阵元2 位于ρ 处。此外，假定一个各向同性的信号源位于阵列近场区域，分别相对于阵元1 和阵元2 位于r和r1 处，信号源相对于参考阵元的角度为θ（关于x轴），距离若s(t) 表示阵元1 接收到的信号复包络，则阵元2接收到的信号包络可以建模为：

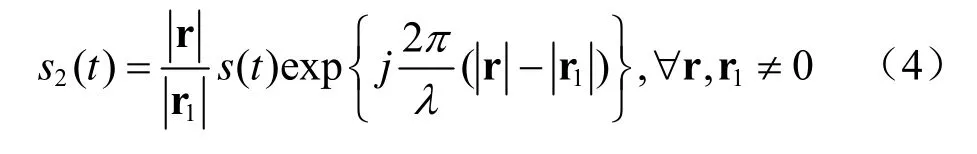
式中，λ为传播波的波长。表明球面波传播的路径传输损耗，指数项表示两个阵元接收信号的相位差。

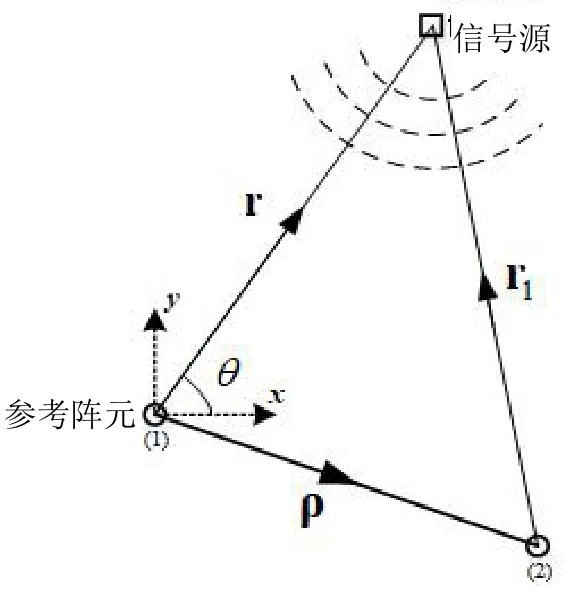
图1 二元阵列接收近场信号示意图

根据平面几何关系易得：

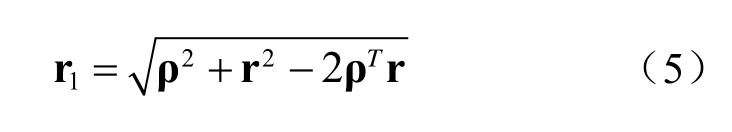
将式（5）代入式（4），阵元2 接收到的信号包络经过处理后可以表示为：

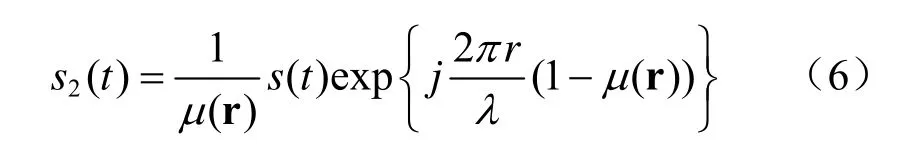
将式（6）推广到任意N元阵列，各阵元相对于参考阵元的坐标分别为 ρ1,...,ρN-1，假设一个近场窄带信号源的位置参数为(θ,r)，r≠ 0，其阵列流形可表示为：

式中，⊙表示Hadamard 积，1N是N×1 维全一矩阵。

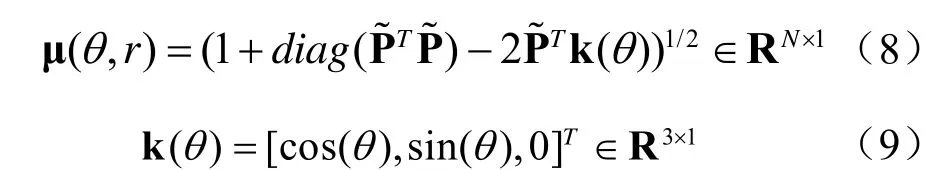
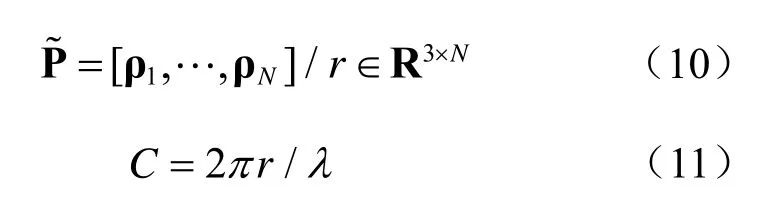
可以看出，近场阵列流形是嵌在N维复数空间的曲面，直接对其研究比较复杂。若假定近场源的距离参数已知，只需对不同距离值的近场阵列流形曲线进行分析即可。值得注意的是，矢量μ 是信源距离r的函数，它取决于距离r相对于阵列规模的大小。

由式（7）可以看出，不同于远场阵列流形 aP(θ)有N0.5固定范数，近场阵列流形的范数是关于信源角度θ函数，因此其图像不在同一个N维超球面上。以七个各向同性阵元组成的均匀线阵为例，对近场阵列流形进行分析，其中阵元间距为半波长，本文后续的讨论也均采用这种阵型。图2给出不同距离参数情况下近场阵列流形与远场阵列流形差异的曲线，距离r为实际距离相对于阵列尺寸的相对值。正如期望的那样，随着信号源距离的增加，远场平面波和近场球面波阵列流形之间的差异接近于零，并且在球面波前最明显的边射处差异最大。图2还表明，不同距离值的θ曲线不存在相交，因此在θ和r中不存在明显的模糊问题。

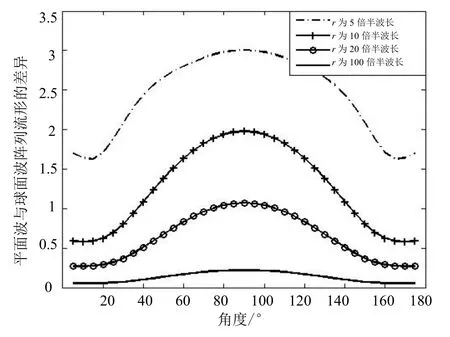
图2 七阵元线阵平面波与球面波阵列流形的差异

2 基于微分几何的近场阵列流形分析

阵列流形是阵列几何结构的直接函数，阵列流形的形状直接影响阵列的参数估计性能。微分几何是运用微积分的理论研究空间曲线和曲面几何性质的数学分支学科，是研究阵列流形形状的基本工具。阵列参数估计的性能中最常用的指标是估计精度和分辨率，这些性能都对应着阵列流形的局部几何特性，如弧长变化率和曲率等。针对第1 节建立的近场阵列流形模型，利用微分几何对弧长变化率和一阶曲率等参数进行推导。

当信号源的距离参数为固定值时，近场阵列流形的目标参数仅剩下角度θ，则有：

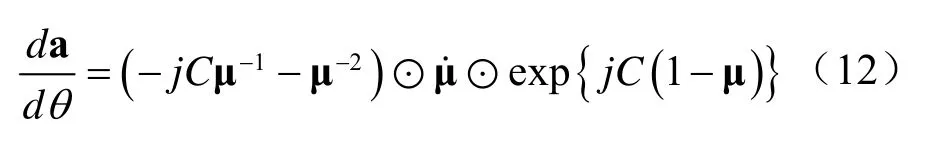
从式（8）可以得出：

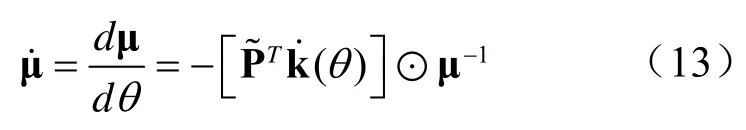
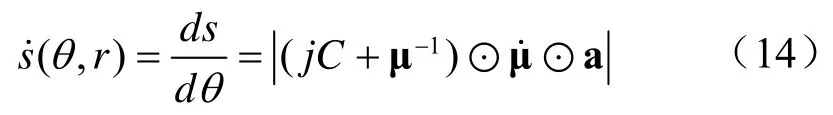
(θ,r)的值可以理解为θ取不同值时阵列敏感度的度量，例如(θ,r)在0θ处的值较大时，0θ附近一个小的角度偏差θΔ 可能会造成阵列响应大的变化Δa，反之亦然。此外，1θ和2θ之间(θ,r)下方的面积表示a(θ1,r)和a(θ2,r)之间的阵列流形弧长，取较大值时在某种程度上意味着更强的分辨性能。图3所示为七阵元线阵在近场源距离不同时函数(θ,r)随θ的变化曲线。很显然，当信号源距离r足够大时，函数曲线逼近于远场情况下的正弦函数。而当辐射源靠近阵列时，端射附近的敏感度和分辨率较低，远离端射的则开始提高。还要注意，对于所有距离值，(θ,r)在角度为0 和π 时取值为0，意味着敏感度和分辨率都为0，根据曲线正则条件，a(θ,r)在这两点上不是正则参数曲线。

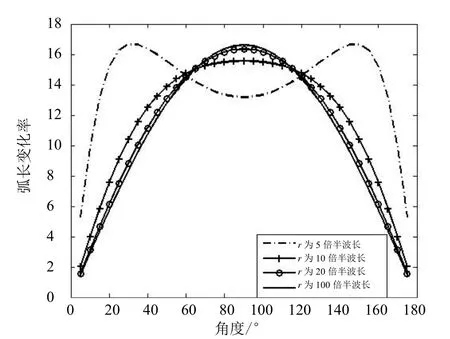
图3 七阵元线阵不同距离 s˙ (θ, r)函数随θ 的变化曲线

微分几何滑动框架第一个坐标轴矢量可以写成：

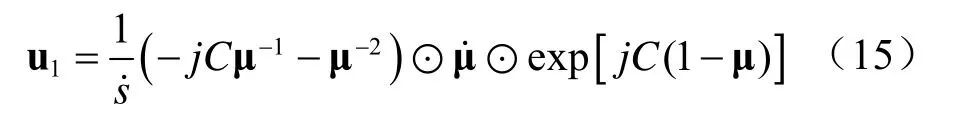
近场阵列流形的一阶曲率表达式κ1(θ,r)可以通过对1u 关于弧长求微分并取范数来获得。经过一系列运算，可以求得：

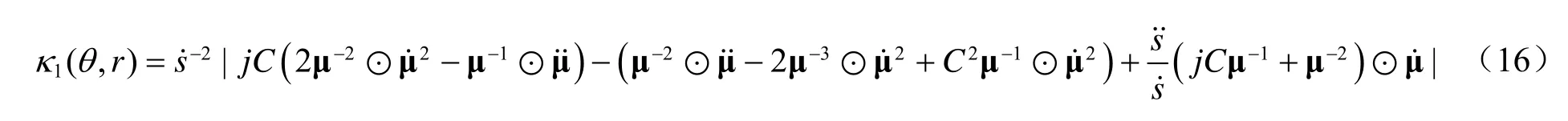
可以看出式（16）的一阶曲率表达式相当复杂，对其进行简化，可得：

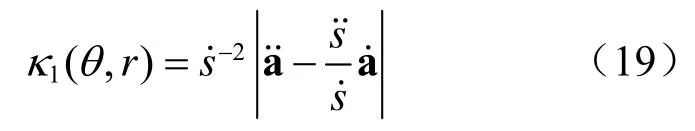
可以预见，即使推导出κ2(θ,r)的表达式，其余2N-3 个曲率的计算也会相当复杂，因此不在这里给出。而幸好只需变量(θ,r)和κ1(θ,r)已知，就可以对阵列参数估计性能进行分析[4]。

七阵元线阵的一阶曲率κ1(θ,r)随角度θ的变化如图4所示，其中θ≠0,π。可以看出，信号源距离参数足够大，即位于阵列远场区域时，阵列流形的一阶曲率为定值，与θ无关，线阵的远场阵列流形为N维复空间中的超螺旋曲线。而当信源靠近阵列时，κ1开始明显偏离于该常数值。因此可以确定，线性阵列的近场阵列流形一般不是超螺旋结构，只有当信源距离增大时逐渐逼近。

图4 七阵元线阵一阶曲率随角度θ 的变化曲线

3 近场参数估计的分辨性能分析

阵列流形曲率越大，阵列的分辨性能越强，因此利用一阶曲率及弧长变化率对分辨率做定量分析是可行的。获得近场阵列流形的s˙(θ,r)和κ1(θ,r)后，继而研究其对子空间类参数估计算法性能的影响。

3.1 阵列流形弧长及估计精度

特征子空间类算法通过阵列观测数据的协方差矩阵 R =E(xxH)分解出信号子空间和噪声子空间。而在实际情况中R是未知的，因此只能用协方差矩阵的最大似然估计来近似，可以通过有限快拍的阵列接收数据获得，这也造成了信号和噪声子空间的扰动，从而不可避免地导致参数估计误差，该误差可以通过参数的CRB 进行分析。假设时空不相关的高斯噪声功率为σ2，快拍数足够大（L≫ 1）时θ的CRB可写作：

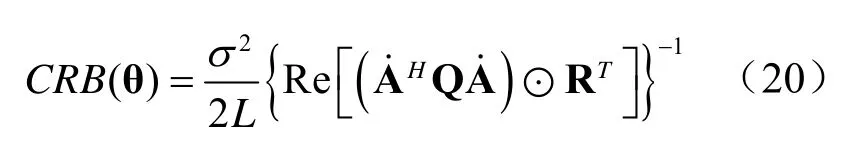
式中，Q = I -A (AHA)-1AH，I 为单位矩阵，A 为阵列流形矩阵，=dA(θ,r)/dθ。与上一节相同，本节在对近场参数估计分辨性能的分析中固定距离参数r，以θ为唯一参数。当近场目标为单位功率的单一信号源时，式（20）可以改写为：

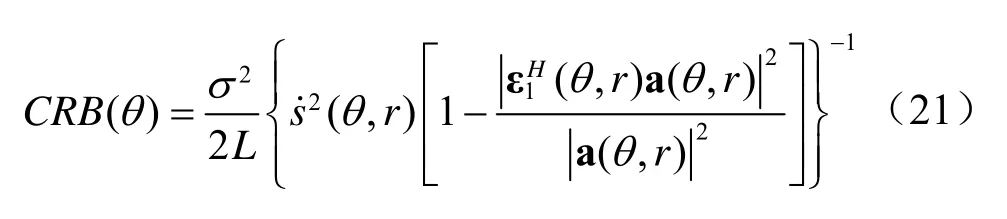
式中，ε1(θ,r)为阵列流形在该点的单位切矢量，可以用代替。自身就是阵列几何结构的函数，从式（21）可以看出阵列流形的弧长在确定无偏估计最小误差方差中的重要性。远场情况(r= ∞)下，阵列接收信号源辐射的平面波时，ε1Ha (θ,r) =0，这一重要性尤为明显，s˙(θ,r)成为唯一影响CRB值的阵列流形特征，即，其中SNR为目标信号的信噪比。

通过分析MUSIC 算法中因有限快拍数导致的参数估计渐近方差表达式，可以进一步证明流形弧长对于参数估计精度的重要性。信源数为1 且功率为单位功率时，渐近方差表达式可写作：

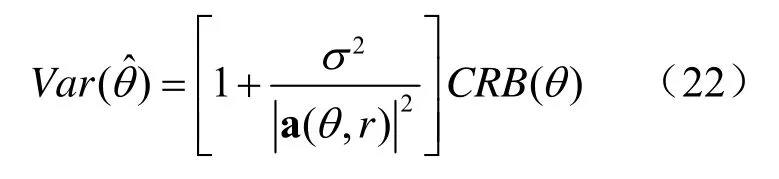
可以看出，高信噪比或阵元数较多时，渐进方差逼近于CRB，并与有类似的依赖性。一般来说，无论何种原因导致阵列流形a(θ0,r)所产生的误差δa，都意味着弧长s0的计算过程中同样造成误差δs，反过来又造成参数估计误差，该误差强正比于。由上可得，阵列几何结构的函数为比较各种阵列结构的参数估计性能提供了一种很有价值的工具。

3.2 阵列流形特性及分辨率

本小节研究阵列流形曲线的微分几何特性对参数估计分辨率性能的影响。假设天线阵列接收到两个距离均为r，角度分别为θ±θΔ 的近场源信号，如图5所示，两个阵列流形端点处分别有一个半径为eσ的不确定球，表示弧长参数分别为s±Δs的参数估计误差。

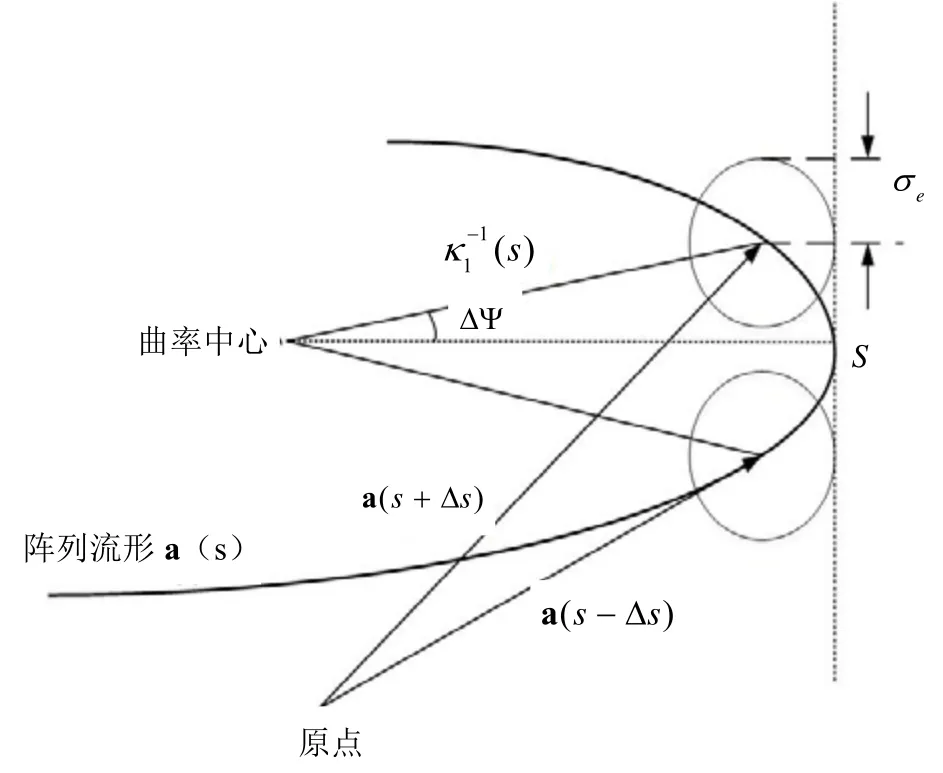
图5 阵列流形误差示意图

假设阵列的分辨性能只受限于有限的快拍数和阵列几何结构，不考虑所采用各种实际参数估计算法的缺点。采用有限次快拍数的观测数据构造协方差矩阵无法完全消除加性噪声。噪声去相关的程度与快拍数成正比，因此建立不确定球半径的模型噪声功率为2σ的背景下阵列接收来波方向为θ的单元功率信号，弧长参数s的无偏估计方差CRB可以表示为：

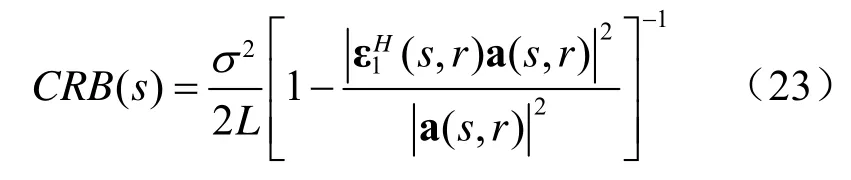
式中，快拍数L≫ 1，证明了上述对不确定球的建模是合理的。可以看出，参数估计误差的方差与噪声功率σ2成正比，与快拍数L成反比。天线阵列接收远场平面波时弧长s的无偏估计方差CRB可以简写为CRB(s) =σ2/2L。虽然这里只考虑了噪声和快拍数的影响，但一般情况下任何误差造成的参数估计影响都可以被模拟。

很明显，空间曲线中足够小的一部分可以用一段圆弧近似表示，圆弧的半径等于曲线在所关注点的一阶曲率的倒数。因此远场情况下流形曲线的所有曲率均为常数[4]，这也使得对远场线阵流形分辨性能的分析被大大简化。近场阵列流形曲线在s±Δs点处的单位切矢量可以用泰勒展开表示为：

式中，κ2(s)是流形曲线的二阶曲率只保留到二阶的项[6]。由于近场阵列流形曲线具有可变曲率，利用圆弧近似近场流形需要满足以下三个条件，当且仅当下列条件满足时，式（24）可以用半径为κ1-1(s)的圆弧有效近似：

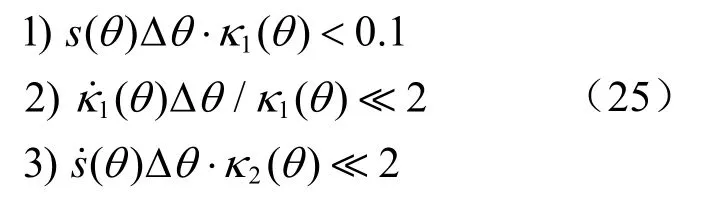
假设上述圆近似是有效的，根据Schmidt 博士提出的分辨率准则[12]，我们可以假定如果切矢量ε1(s)与不确定球不相交时，则可以成功分辨角度参数分别为θ±θΔ 的两个近场源。将阵列流形的一阶曲率引入该准则，可得：

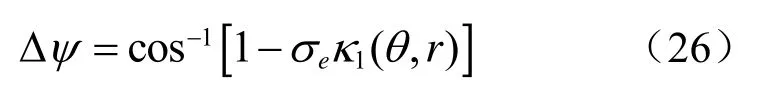
值得注意的是，Δψ=Δs·κ1(θ,r)，利用σe的模型，可以推导出间隔Δθ的两个目标所需的信噪比表达式：

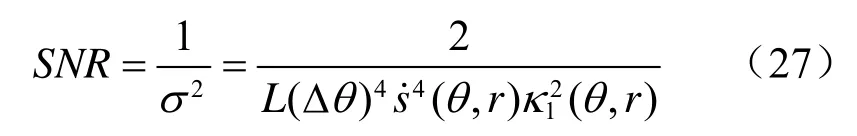
式（27）将天线的分辨能力与阵列流形的弧长变化率和一阶曲率结合起来，可看出s˙(θ,r)对所需SNR 的影响更大。

图6所示的是七阵元组成的均匀线阵分辨不同距离环上角度为θ±0.5°的近场源所需信噪比的曲线，其中快拍数为500，0°＜θ＜180°。该情景下满足式（25）的三个条件，因此圆近似有效。可以看出，分辨阵列端射方向的信号源所需信噪比趋于无穷大，这一点也可以通过θ= 0°, 180°时来验证，表明阵列轴向的分辨率为0。还要注意的是，近场源来波方向靠近阵列法向时，距离越大所需的可分辨信噪比越低，这既是因为发射源可以在较低的信噪比(在阵列基准处测量)下被分辨，也是由于的变化造成的。

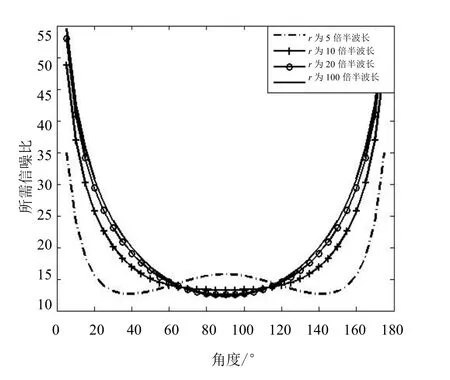
图6 分辨相邻信号所需的SNR 曲线

4 结论

本文以雷达和声呐系统的目标定位为背景，采用微分几何研究了存在近场辐射源情况下由全向传感器组成的阵列接收近场源信号阵列流形，并以均匀线阵为例给出阵列流形弧长变化率和一阶曲率以信源角度和距离参数的数学表达式，同时讨论了参数估计的分辨特性，为近场参数估计新算法的提出和阵列结构的优化设计提供了理论依据。