SC-FDE系统中信道估计和均衡算法的研究和实现

雷一昇

（中国电子科技集团公司第二十研究所，西安 710068）

0 引言

单载波频域均衡（Single Carrier-Frequency Domain Equalization，SC-FDE）技术克服了正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术的峰均功率比高、对载波频率偏移和相位噪声敏感的缺陷，且同时具备了正交频分复用技术频谱利用率高、对抗码间串扰能力强和带宽扩展性好的优势，已经成为下一代移动通信系统的关键技术[1]。与一般的时域均衡不同，SC-FDE 在均衡时必须获得各子信道衰落因子的幅度和相位信息，因此信道估计和均衡算法一直是该技术的研究重点之一。信道估计通常采用离散傅立叶变换（Discrete Fourier Transform，DFT）插值算法获取，该算法在结构上比较复杂，计算量也相对较大。针对该问题，本文采用格雷互补序列作为信道估计训练序列，该序列相关电路结构比较简单，有利于工程实现，并且大幅降低了运算复杂度和处理时延。结合最小均方误差（Minimum Mean Square Error，MMSE）均衡算法对均衡估计参数计算步骤进行详细推导，最后对时域滤波的原理进行了说明和仿真验证。

1 信道估计算法原理

SC-FDE 均衡技术有效地结合了OFDM 和单载波传输的优点[2]。在OFDM 系统中，通过引入循环前缀（Cyclic Prefix，CP）作为保护间隔来消除子载波之间的干扰[3]。而在SC-FDE 系统中，它的帧结构有两种方案：一种是帧结构中采用CP 的SC-FDE 系统，CP 的产生及插入与OFDM 系统一致；另外一种是在帧结构中插入独特字（Unique Word，UW），相比于传统的CP 序列，UW 序列是可以选择的序列，且在传输过程中序列一直不变，因此可以通过UW 序列完成相偏、频偏和信噪比等参数估计[4]。本文采用UW 序列构造帧结构，具体数据帧结构如图1所示。

图1 数据的帧结构框图

数据帧结构中同步头序列和同步尾序列分别用来估计信道频率响应。以同步头序列估计信道频率响应为例，具体计算步骤为：首先对接收同步头序列进行快速傅立叶变换（Fast Fourier Transform，FFT），得到的结果与本地同步头序列FFT 变换的结果进行相除，可以得到HNg，将信道估计值HNg进行Ng点快速傅立叶逆变换（Inverse Fast Fourier Transform，IFFT）之后，在序列后边添加N-Ng个零，得到序列hn，对hn进行N点FFT 变换，可以得到所需的信道频率响应HN。

从图2中可以看出利用DFT插值方法计算信道频率响应比较复杂，涉及到多次FFT 和IFFT 运算，虽然FFT 和IFFT 运算IP 核已经非常成熟，但实现时会消耗大量硬件资源，增加处理时延，不利于流水线设计[5]。采用DFT 插值算法估计信道频率响应本质上是将时域估计转换为频域估计，时域估计采用接收同步序列和本地同步序列进行滑动复相关，由于整个计算过程中接收序列采用幅值复相关，实现时更加耗费资源，不利于工程实现。

本文在帧结构设计过程中，同步头序列和同步尾序列采用格雷互补序列对，该序列的自相关之和为冲激函数，并且相关电路结构比较简单，工程实现节省资源，图3为格雷互补序列相关器电路结构。

从图3中可以看出相比于一般的时域相关器，格雷相关器能减小资源开销，例如对于长度L=2N的格雷序列，其相关电路包含了2N-1个延迟单元、N个乘法器、2×N个加法器，而传统的相关器需要2N-1个延迟单元和2N个复数乘法器和2N-1个加法器，相比于传统相关器大大节省了资源。

2 频域均衡算法原理

均衡可以消除或减少由时延扩展引起的码间串扰，均衡技术可以分为时域均衡和频域均衡两种。图4为频域线性均衡器结构，均衡器输入数据经过FFT 变换后与均衡器系数相乘，接着经过IFFT 变换完成频域均衡。

在均衡处理过程中，如果按照使均衡器输出端的均方误差最小的准则去调节横向滤波器系数，这种调节依据称为最小均方误差准则[6]。如图4所示，假设输入信号为rn，均衡器输出信号为dn，第n个数据的误差可以表示为：

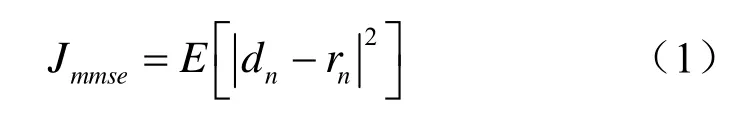
为了得到合适Ck使式（1）值最小，利用帕赛瓦尔定理，可将式（1）化简为：

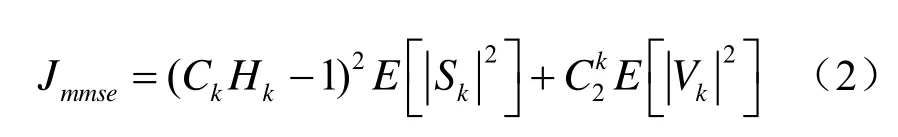
对式（2）进行求导运算，并令其值为0，可得到：

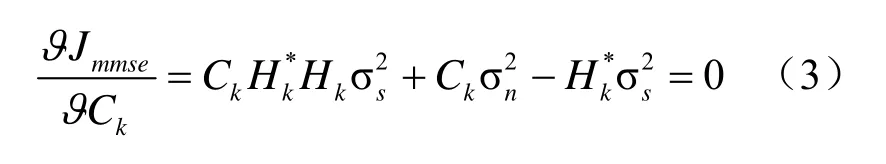
对式（3）求解可得到：

式（4）中Hk表示信道传输函数，σ2n表示噪声功率，σ2s表示发射信号功率。从式（4）中可以看出，最小均方误差准则中综合考虑了码间串扰和噪声干扰的影响。

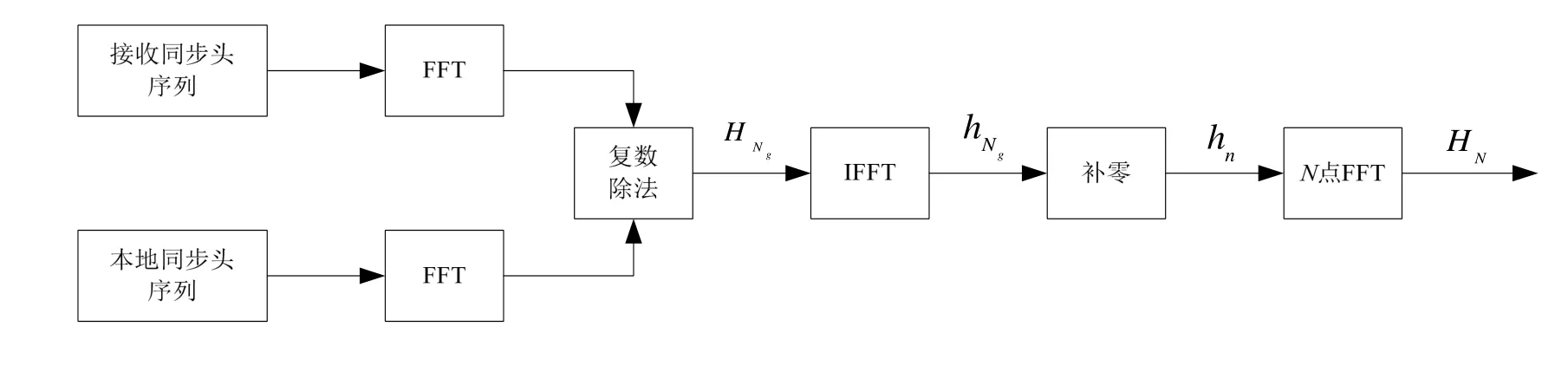
图2 DFT 插值方法结构框图

图3 Golay 互补序列相关器电路结构

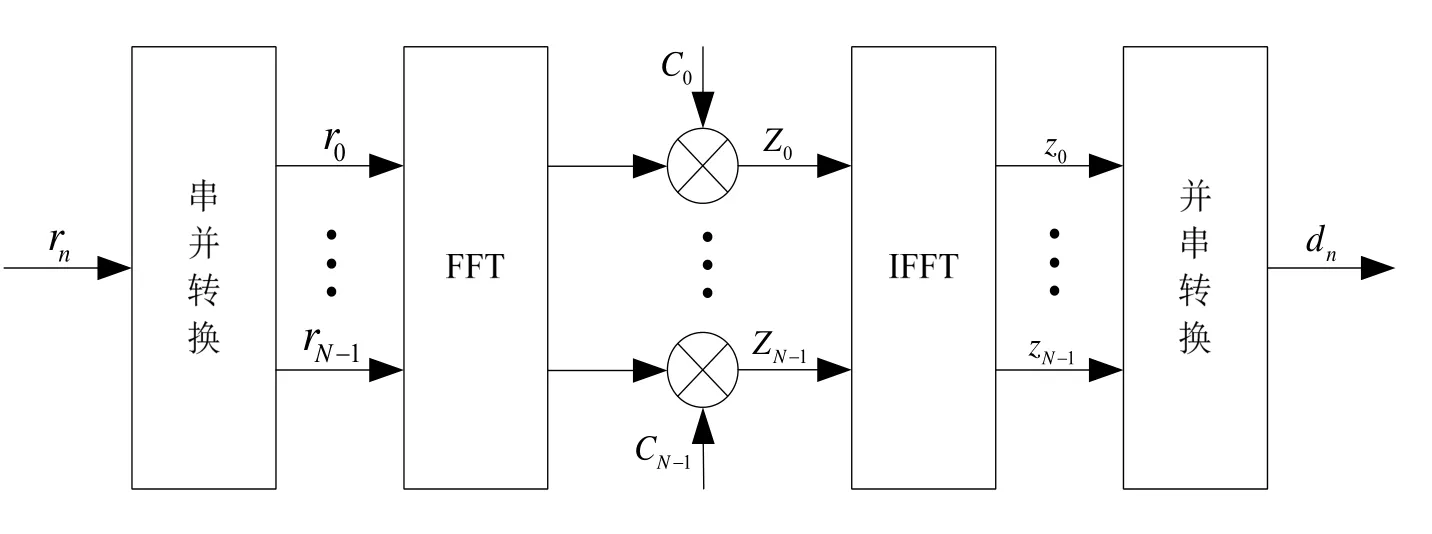
图4 性均衡器原理框图

3 信道估计和频域均衡实现

本文采用MMSE 均衡算法，获取MMSE 均衡估计参数是均衡处理中最重要的部分，具体计算步骤下文进行详细推导。同步头相关和同步尾相关采用上文提到的格雷互补序列相关电路实现，图5为MMSE 均衡估计参数计算框图。

首先对同步头相关结果hhead和同步尾相关结果htail进行FFT 变换，变换长度为每个数据子块的长度N，可得：

对同步头相关结果hhead和同步尾相关结果htail相加计算平均值：

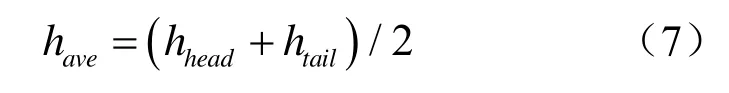
对have进行时域滤波，得到，然后进行FFT变换和取共轭处理，得到信道传输函数。信道估计噪声功率σn2和发射信号功率σs2分别为：

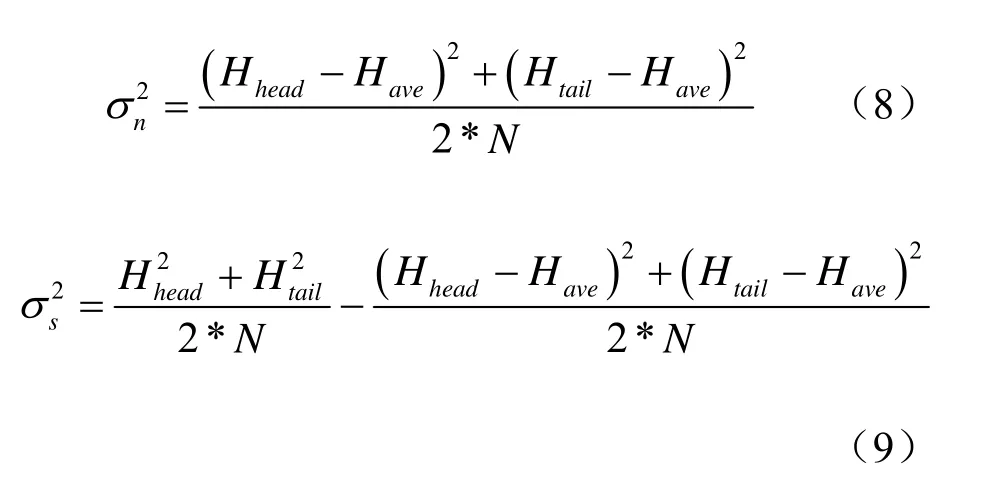
最后根据式（4）得到MMSE 均衡系数为：

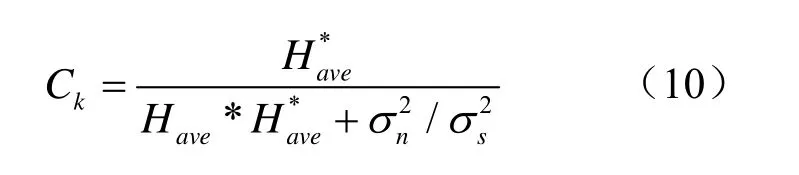
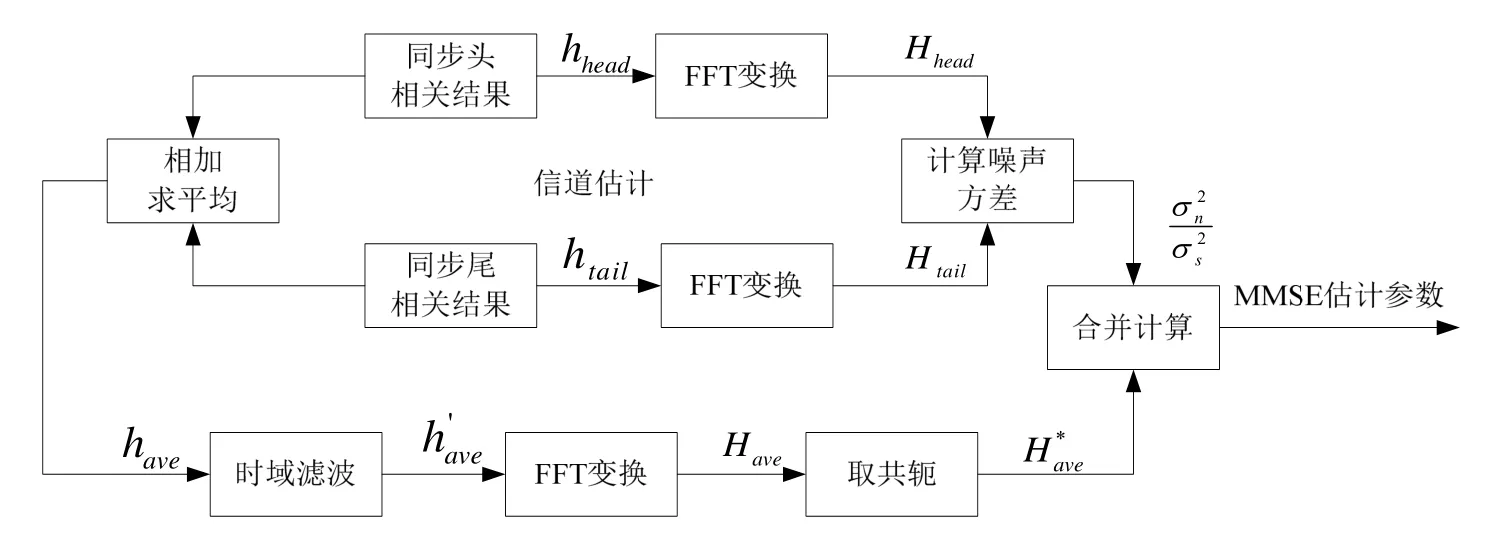
图5 MMSE 均衡估计参数计算框图

在计算信道频率响应时由于在频域中高斯白噪声和实际信道响应难以区分，不能消除噪声对实际信道估计的影响，因此可以采用时域滤波的方法来降低噪声的影响。本文采用的时域滤波算法主要通过设置噪声门限滤除同步相关结果中的噪声。

首先计算噪声门限。将时域同步序列相关结果进行累加计算平均值，然后求开方可得噪声门限为：

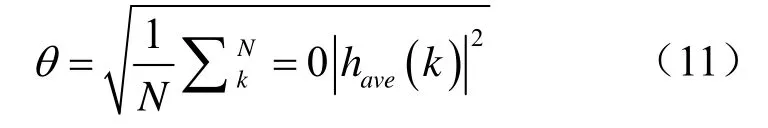
然后进行时域滤波。对信道冲激响应ha ve（k）根据噪声门限θ进行滤波，可得式（12）：

利用Matlab 对时域滤波算法进行仿真，时域滤波前信道冲激响应如图6所示，时域滤波后信道冲激响应如图7所示。

从图6和图7可以看出，经过时域滤波后噪声分量基本被滤除，并且多径分量仍得到保存。通过Matlab 对整个发射接收系统仿真，时域滤波算法在多径信道下系统接收性能提高了近2 dB，对整个系统接收性能提升起到了非常关键的作用。

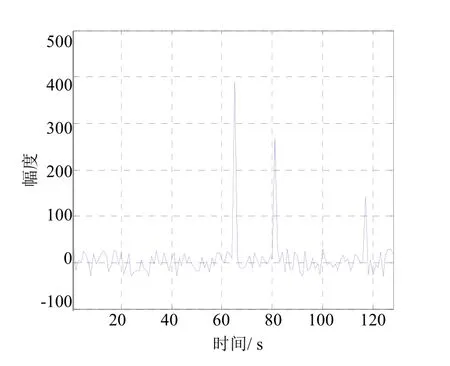
图6 时域滤波前信道冲激响应

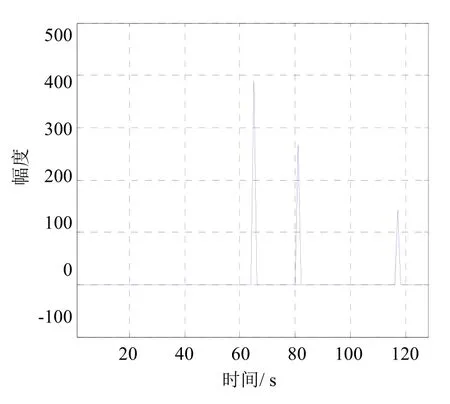
图7 时域滤波后的信道冲激响应

4 总结

本文首先分析了传统DFT 插值算法的缺点，提出了同步序列采用格雷互补序列的信道估计方法，

该方法实现电路非常节省资源。然后结合MMSE 均衡算法，对均衡估计参数计算步骤进行了详细推导。最后对时域滤波算法原理进行说明，通过Matlab 软件进行仿真验证，该方法能够将噪声分量滤除，在多径信道下采用时域滤波接收性能提升了近2 dB，具有较高的参考和应用价值。